一道市质检题的解法探究

黄清波

(福建省南安市国光中学)

三角形问题在各类考试中备受青睐,命题方式灵活多样,试题内容活泼、新颖,是一个稳定的高频考点.解决这类问题的基本方法:三角法、向量法、坐标法和平几法.本文以泉州市2024届高中毕业班质量监测第19题为例展开探究,谈谈对各种方法的几点理解,希望对师生今后学习能够产生一定启示.

一、题目展示

△ABC的内角A,B,C所对的边分别为a,b,c,且满足ccosB+(b+2a)cosC=0.

(1)求C;

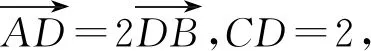
【分析】本题主要考查解三角形、三角恒等变换等基础知识;考查推理论证、运算求解等能力,考查化归转化、数形结合、函数与方程等思想,体现综合性与应用性,导向对发展直观想象、逻辑推理及数学运算等核心素养的关注.第1问5分,市平均分3.21分,第2问7分,市平均分1.21分,学生得分率较低.本题蕴含着丰富的数学思想方法,耐人寻味.

二、解法探究

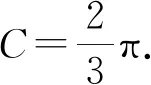
(一)三角法

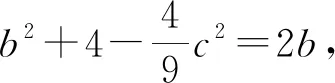
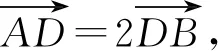
【小结】“三角法”是利用正弦定理、余弦定理、三角形内角和定理、三角形面积公式,适时、适度运用“角化边”或“边化角”,同时结合三角函数的性质、三角恒等变换公式、同角三角函数基本关系式等进行化简与求值．此法是解决三角形问题的常用解法.

(二)向量法

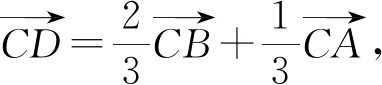
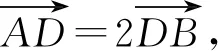
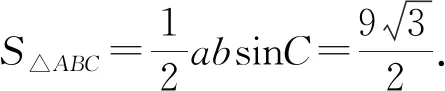
【小结】“向量法”是指非坐标向量法,与坐标法相比,它无需要建立坐标系,且运算简捷、可操作性强,更能体现向量的魅力等优点.新教材把向量和解三角形结合起来,突出了它在解三角形中的重要作用.

(三)坐标法

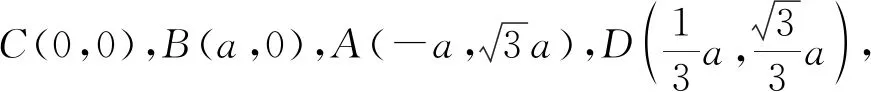
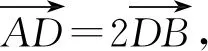
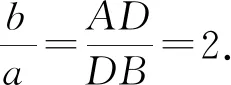
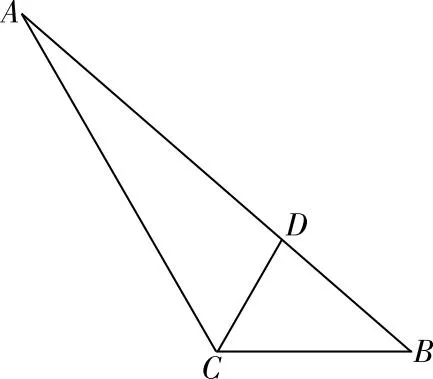
如图,以C为原点,CB所在直线为x轴建系.

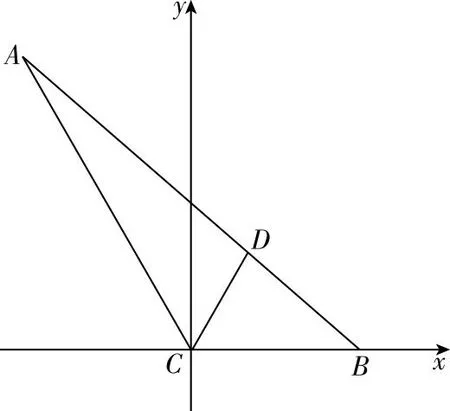
【小结】“坐标法”根据三角形的结构特征,合理构建平面直角坐标系,找出三角形相应顶点的坐标,便能快捷解得三角形的各个要素.解题思路明确、清晰,解题过程简洁.此法将数与形完美地结合起来,降低了思维难度,解题有一定的规律性,便于学生掌握.

(四)平面几何法

【思路四】过D点作DE∥AC交CB于点E.易得△CDE为等边三角形,另由三角形相似对应边成比例,求出a,b,进而求出面积.

解法4：过D点作DE∥AC交CB于点E.

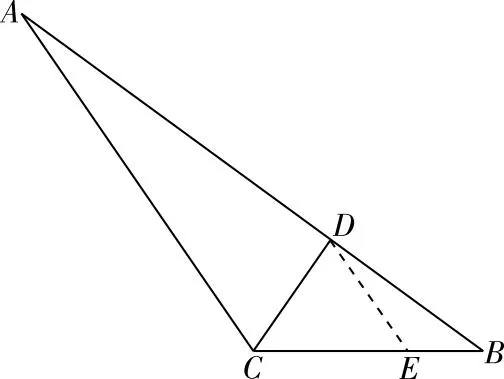
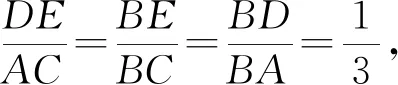
【小结】“平几法”是以逻辑推理作为工具解决问题,解题过程中经常要引入辅助线和回忆大量的几何定理公理,对学生的空间想象能力和逻辑推理能力要求较高,运用得好,往往可以巧妙地避开复杂的运算,简化解题过程.

三、试题链接

(1)求bc;

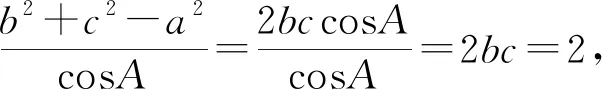
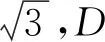
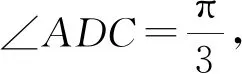
(2)若b2+c2=8,求b,c.

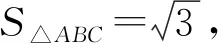
过A作AE⊥BC,垂足为E,如图所示:

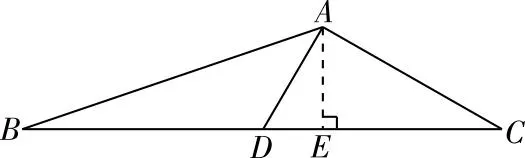
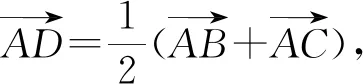
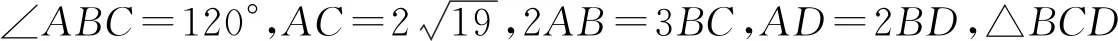
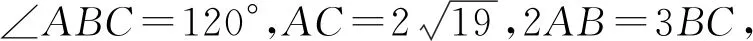
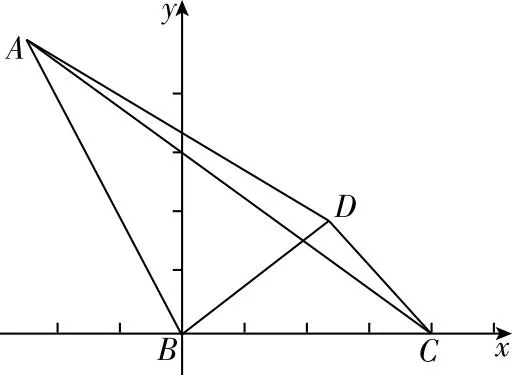
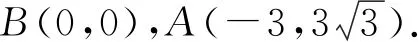
以上几个题未给出多种解法,留给读者联想借鉴完成.

总之,解三角形的“多法”的准确定位是并举!即不宜人为地、凭主观划分它们的优劣,而应具体问题具体分析.哪怕受教学时间的限制,在课堂上尽可“择其善者而从之”,但对另外的方法应稍作提示引导,让学生在课下尝试、讨论,并对“多法”进行比较.这对学生能力的提高大有裨益.