考虑滑流效应的静气动弹性分析研究

周博康 刘峰博 周磊 梁益华

摘要：随着电推技术的快速发展，分布式螺旋桨推进技术在中小型飞行器中的应用研究更加深入。针对大展弦比机翼柔性较大、变形大问题，开展螺旋桨滑流效应与机翼弹性变形的复杂气动结构耦合研究。基于自研CFD软件，采用激励盘代替螺旋桨计算定常气动力，通过RBF方法进行气动力和位移的双向插值，结构计算基于开源程序TACS，完成分布式多旋翼-机翼靜气弹分析方法及程序的建立。重点研究螺旋桨旋转方向和转速对机翼气动特性的影响，结果表明，螺旋桨顺时针旋转时阻力更大，旋转方向对机翼升力和变形量影响较小；螺旋桨转速越高，翼尖位置处的静气弹变形越明显，导致机翼表面的气动力重新分布。

关键词：大展弦比；分布式；激励盘；滑流影响；CFD/CSD松耦合计算

中图分类号：TB126    文献标志码：A    文章编号：1671-0797（2024）07-0033-04

DOI：10.19514/j.cnki.cn32-1628/tm.2024.07.009

0    引言

近年来，电推进技术在汽车、动车等传统运输工具领域得到了较为广泛的应用。而航空飞行器对轻量化、可靠性、能源能量密度、发动机功率等要求较高，因此电推进技术在航空领域的应用仍处于探索阶段[1]。目前，应用于中小型飞行器的分布式螺旋桨推进技术成为航空领域的研究热点。此类飞行器的机翼通常具有大展弦比、柔性大的特点，静气弹变形较大，同时螺旋桨导致的滑流效应引起机翼的气动载荷发生变化，气动弹性和滑流效应的耦合更加复杂[2]。

针对柔性机翼的气动弹性问题，徐敏等人发展了一种CFD/CSD松耦合方法，以M6机翼为研究对象，计算了马赫数0.839 5、迎角5.06°状态下的静气弹结构响应以及气动特性[3]；谢长川等人通过升力线方法求解机翼上的定常气动力，并结合有限元静力学工具建立了一种螺旋桨机翼气动弹性问题的快速求解方法[4]；唐佳栋等人采用松耦合方法研究了螺旋桨旋转引起的流场扰动对机翼的影响[5]。

本文针对分布式螺旋桨机翼，采用CFD/CSD松耦合方法，在静气弹计算的基础上，分析螺旋桨滑流效应对机翼的影响。

1    数值模拟方法

1.1    激励盘模型

针对螺旋桨滑流问题的数值模拟采用激励盘模型，在桨盘位置处通过一个无厚度的圆盘代替桨盘。激励盘法能够极大地降低网格生成难度及计算成本，在仅考虑定常状态下的流场而不考虑桨尖引起的复杂流动时，能够保证精度，同时减少计算量。

激励盘上的载荷分布包括常数分布、线性分布和非线性分布等。本文采用Goldstein载荷分布的激励盘法对滑流进行模拟。为了验证该方法计算气动力的准确性，以单螺旋桨PROWIM模型为例，采用自研软件计算了马赫数0.145、0°迎角下的展向升力系数。如图1所示，可以发现，机翼上下翼面的升力环量与试验值较为接近。

1.2    气动结构耦合分析流程

针对分布式螺旋桨机翼静气弹分析，搭建CFD/CSD松耦合计算流程。松耦合保持了CFD和CSD模块的独立性，只需通过数据插值技术增加气动力和位移的数据交换即可组成耦合系统，从而降低计算复杂度。其基本流程如下：

1）根据初始气动网格和计算状态在CFD求解器中计算流场；

2）利用RBF插值方法将CFD计算得到的耦合界面上的气动力插值到CSD网格对应的节点上；

3）通过有限元求解器计算施加气动力载荷后物面网格点上产生的节点位移；

4）比较第n步和n-1步有限元计算得到的节点最大位移变化量，若满足位移收敛条件，则完成计算，未达到收敛标准则继续迭代计算；

5）再次利用RBF插值将有限元网格节点上的位移插值到气动网格上；

6）通过网格变形技术对流场域网格进行更新，直到达到位移收敛标准，则完成迭代。

本文CFD计算采用自研软件，通过激励盘法模拟螺旋桨。湍流模型选择SA模型，空间离散格式选择ROE格式。CSD计算基于开源有限元求解器TACS进行计算，通过RBF插值技术在耦合界面上进行节点位移和气动力的交换。具体流程如图2所示。

2    计算模型

2.1    几何模型

本文的研究对象为分布式螺旋桨大展弦比机翼，机翼结构为双梁多肋型，翼型为NACA 63717，展长5 m，展弦比15。机翼主要由前后梁、翼肋和蒙皮组成，桨盘中心距机翼前缘0.2 m，距离翼根分别为1.2、3.1、5 m。在计算中仅考虑机翼的变形，不考虑桨叶变形。

2.2    CFD计算模型

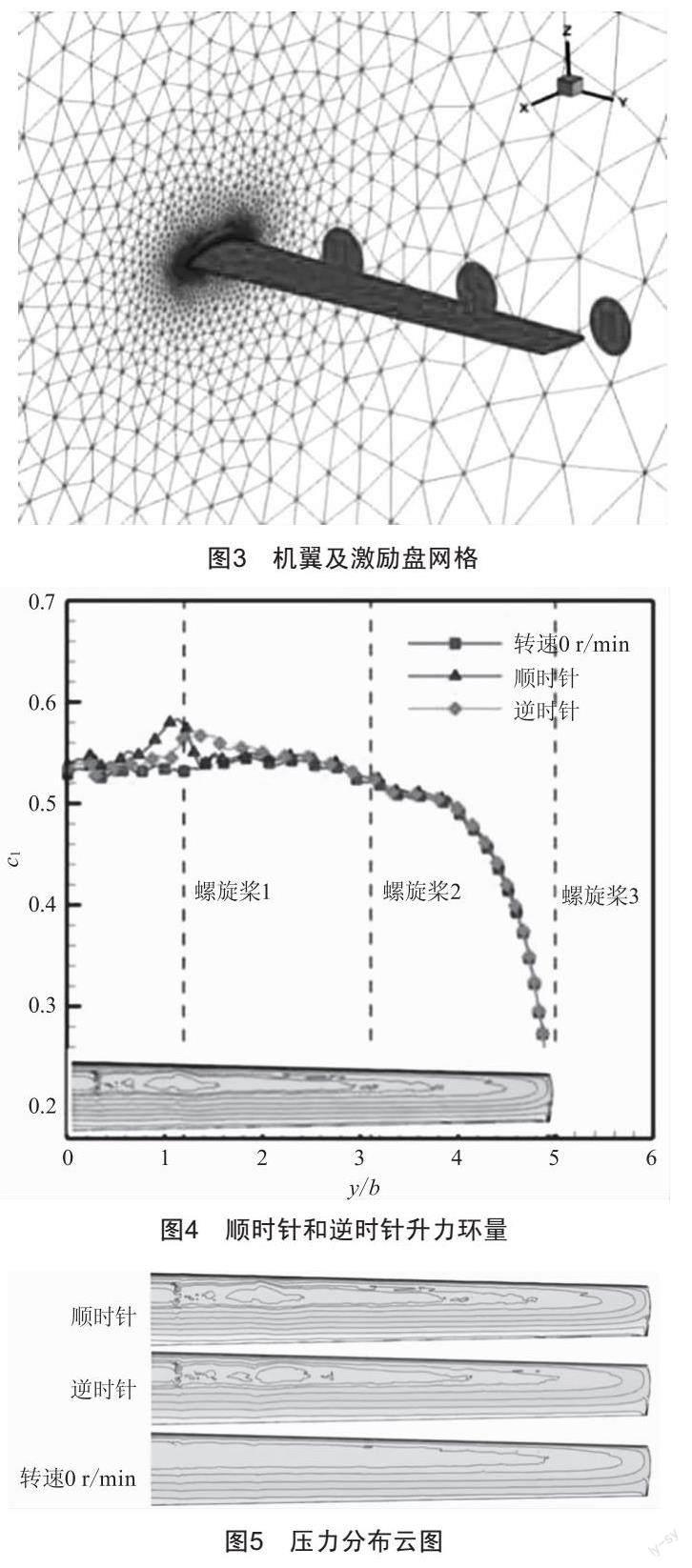
在CFD计算中，暂不考虑螺旋桨桨毂。首先采用Pointwise生成粗、中、细三套非结构网格进行网格无关性验证。其中，中等网格点数为194万，激励盘网格数设置为径向15个点、周向75个点，网格示意图如图3所示。计算马赫数0.233，采用定升力0.55计算，可以得到，网格点数由91万增加到194万时，阻力变化量较大，将网格点数增加到292万，得到的阻力变化量较小，基本达到计算精度要求。因此，选用网格点数为292万的网格进行后续静气弹计算。

2.3    CSD计算模型

在有限元计算中，为了降低计算量，将实际结构简化为由前后翼梁、翼肋和蒙皮组成的翼盒模型。翼根与机身为刚性连接，因此对翼根处的单元节点施加固定约束。有限元单元采用不同厚度的CTRIA3和CQUAD4单元进行划分，翼梁处单元厚度为14 mm，翼肋单元为3 mm，蒙皮单元为2 mm。

3    结果及分析

针对螺旋桨旋转方向和转速对机翼气动特性的影响，本文计算了0、2 548、4 548、6 548 r/min四种转速下机翼的流场和结构变形。

3.1    螺旋桨旋转方向对机翼气动特性的影响

为了分析螺旋桨旋转方向对机翼的影响，选择第3组转速，通过改变激励盘的前进比正负，实现螺旋桨顺时针和逆时针旋转。比较发现，螺旋桨旋转方向对机翼变形量影响不大，顺时针旋转时，机翼的最大变形量为0.197 7 m，逆时针旋转时，机翼最大变形量为0.197 0 m。图4为顺时针、逆时针和无滑流状态下机翼升力环量，虚线为桨盘中心的位置。可以看出，顺时针和逆时针旋转方向升力差别不大，因而变形量基本一致。对于阻力而言，顺时针阻力系数为0.018 6，逆时针阻力系数为0.017 65，原因在于逆时针旋转时，螺旋桨引起的气流旋转方向与翼尖涡方向相反，削弱了翼尖涡的强度，降低了机翼的诱导阻力。从图5三种情况下的压力分布云图可以得到，螺旋桨滑流引起后方的上翼面出现较大低压区，顺时针旋转时，升力的峰值出现在螺旋桨后方靠近翼根的一侧，而逆时针旋转时，升力峰值出现在螺旋桨后方靠近翼梢的一侧。

3.2    螺旋桨转速对机翼气动特性的影响

为了分析螺旋桨转速对机翼升阻力特性的影响，对转速为0（无滑流）、2 548、4 548、6 548 r/min进行静气弹计算。达到收敛条件后，得到不同转速下的升阻力。随着转速的增大，升力和阻力的斜率逐渐增大，主要原因在于转速越高，引起的滑流效应越明显，气流经过螺旋桨加速加旋后，增大了机翼的当地气流迎角，影响压力分布，尤其是螺旋桨后方的机翼，受到滑流影响更大。

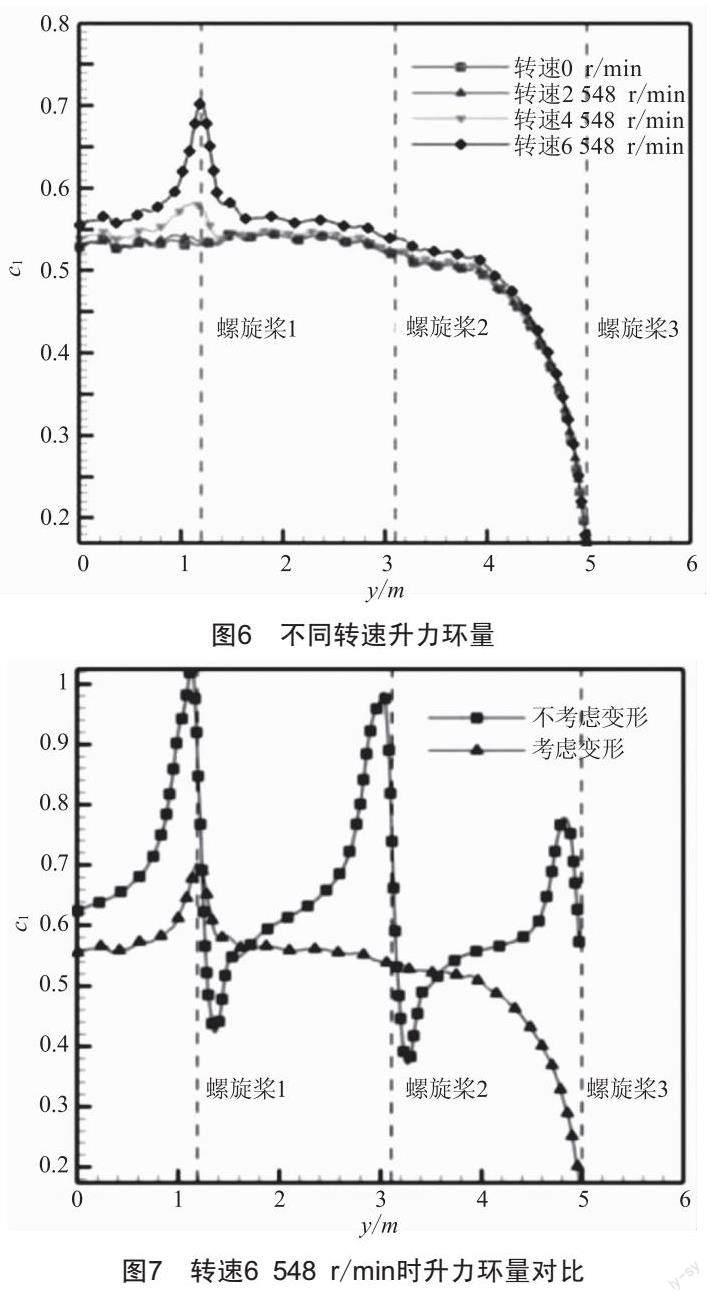
图6为四种转速下机翼的升力环量，转速增大时，螺旋桨后方的升力明显增大。值得注意的是，仅在靠近翼根的一侧出现了较为明显的升力峰值，而在螺旋桨2和螺旋桨3的位置并无明显峰值。

为进一步分析导致该现象的原因，选取转速6 548 r/min，分别计算考虑静气弹变形与不考虑变形的升力。結果如图7所示，没有考虑变形下的升力环量，即视机翼为刚性；考虑变形的升力环量，即为柔性机翼。可以看出，不考虑静气弹变形时，在三个螺旋桨的后方均出现了明显的升力峰值，而对于柔性机翼，仅在螺旋桨1处存在明显的升力峰值，靠近翼尖位置处升力峰值消失。主要原因在于，螺旋桨1比较靠近翼根处，机翼刚度较大，变形小，机翼的扭转角较小，因而升力相较于无变形情况下有所降低，而螺旋桨2和螺旋桨3两个螺旋桨靠近翼梢，机翼刚度较小，滑流引起的升力增量被翼梁、翼肋和蒙皮传递到机翼其他位置，因而升力峰值几乎消失。可见，滑流效应和静气弹变形存在紧密的耦合关系。

4    结论

本文采用自研CFD软件和开源结构求解器TACS搭建了CFD/CSD松耦合求解流程。针对分布式大展弦比机翼，通过激励盘模型进行滑流计算，研究了静气弹和滑流效应耦合情况下，螺旋桨旋转方向和转速对机翼气动特性和变形的影响，主要结论如下：

1）螺旋桨顺时针和逆时针旋转的阻力由于翼尖涡的影响略有差异，而升力大小基本一致，因而机翼上的载荷较为接近，变形量基本相同。

2）随着螺旋桨转速的均匀增大，滑流效应对机翼的影响更加明显，机翼升阻力曲线的斜率更大；靠近翼根位置处，机翼刚度较大，存在明显的升力峰值，翼梢位置处，机翼刚度较小，变形较大，升力峰值几乎消失。因此，静气弹变形会对机翼的载荷分布产生一定影响。

[参考文献]

[1] 纪宇晗，孙侠生，俞笑，等.双碳战略下的新能源航空发展展望[J].航空科学技术，2022，33（12）：1-11.

[2] 张宝升，王军利，刘志远，等.大展弦比复合材料机翼几何非线性静气动弹性研究[J].复合材料科学与工程，2023（4）：78-86.

[3] 徐敏，安效明，陈士橹.一种CFD/CSD耦合计算方法[J].航空学报，2006（1）：33-37.

[4] 谢长川，张利娟，刘燚，等.螺旋桨/大柔性机翼静气动弹性快速分析方法[J].北京航空航天大学学报，2015，41（1）：147-153.

[5] 唐佳栋，王高峰，叶尚军，等.基于螺旋桨滑流效应的大展弦比机翼气动弹性分析[J].计算力学学报，2023，40（1）：21-26.

收稿日期：2023-12-19

作者简介：周博康（1995—），男，陕西汉中人，硕士研究生，助理工程师，研究方向：流固耦合。