高速铁路跨度250 m级连续刚构桥长波不平顺控制研究

2024-04-12游颖川谢海清

铁道标准设计 2024年4期

游颖川，谢海清，卢斌，张迅

(1.西南交通大学桥梁工程系,成都 610031; 2.中铁二院工程集团有限责任公司,成都 610031)

引言

随着新时代西部大开发和“交通强国”战略的推进,我国高速铁路路网逐步由中东部平原丘陵地区向西部山区拓展。受我国西部山区自然条件制约和铁路自身技术标准的限制,当线路跨越深沟峡谷时,山区高速铁路有时只能采用高墩大跨桥梁[1-2]通过。对于艰险山区峡谷地形墩高150 m、跨径250 m的连续刚构桥,其可提供的线路高程相当于主跨400 m级上承式拱桥。因此,主跨250 m级超高墩大跨度连续刚构桥可与大跨度混凝土拱桥形成竞争,极大地增加艰险山区高速铁路选线的自由度。

大跨度连续刚构桥通常兼有“大跨”和“高墩”两个典型结构特点。因此,这类桥梁受到收缩徐变以及温度效应引起的附加变形往往更加突出,使轨道长波不平顺加剧,从而影响列车的行车性能。

我国对轨道长波不平顺的静态测量主要借鉴德国的矢距差法[3]。有研究表明:对于大跨度桥梁,采用矢距差法测量的结果往往超出不平顺管理值,但列车实际运营状况良好。为提出更为准确的轨道长波不平顺控制标准,大量学者开展了相关研究[4-7]。朱志辉等[7]在分析大跨度拱桥因温度效应引起的附加变形对列车走行性的影响时,建议以竖曲线半径代替矢距差法作为验收指标;WANG等[8]基于轨道几何不平顺检测数据提出一个桥梁变形预测模型,并分析了温度、徐变等对高速铁路桥梁长期变形的影响;JIANG等[9]研究了桥墩沉降与轨道变形的映射关系,以及对高速列车行车性能的影响。田新宇、杨飞等[10-11]针对时速300～350 km运营期高速铁路的长波高低不平顺,提出了波长评价方式和建议值,以及相应的幅值和均值管理标准;郑晓龙、徐昕宇等[12-13]基于弦测法研究了上承式拱桥上列车的行车安全性和桥面变形限值,研究表明,30～50 m弦测法能够较好地反映列车通过上承式拱桥时的加速度响应变化规律。

当前,国内外针对跨度大于200 m级的高墩大跨度连续刚构桥综合考虑收缩徐变和温度效应影响的车桥耦合动力性能研究较少,相关长波不平顺评价标准也不明确。本研究以一座试设计的主跨250 m高速铁路连续刚构为研究对象,通过Midas /civil软件计算了连续刚构温度变形和收缩徐变变形,采用列车-线路-桥梁动力学仿真软件分析了考虑不同附加变形倍数下的车桥动力响应。选取中点弦测法作为评价长波不平顺的依据,得到了该跨度下连续刚构桥面变形和等效不平顺的弦测限值。

1 中点弦测法

1.1 弦测法原理

图1 中点弦测法示意Fig.1 Schematic of midpoint chord measurement method

(1)

式中,M为弦测矢量值,即线段PPi长度;y′、yi-L和yi+L分别为点P′、Pi-L和Pi+L的竖坐标。

1.2 有效波长范围

由于中点弦测法采用固定弦测长度进行测量,因此对于过长和过短波长的轨道不平顺不能有效测量。在评价连续刚构长波不平顺时,明确各弦测长度所对应的有效波长范围有利于选取合理的弦测长度,从而获得较好的车体响应匹配性。各弦测长度的有效波长范围可根据传递函数进行计算,由式(1)可得传递函数的表达式为[15]

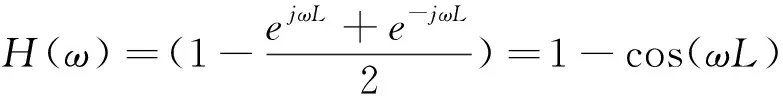
(2)

式中,ω为空间频率;j为单位虚数;L为半弦长。

由式(2)可知,传递函数主要受轨道不平顺波长λ(λ=2π/ω)和L的影响,函数值在0～2.0之间。同时,传递函数中不含虚部,说明了中点弦测法的测量结果与实际结果不存在相位差,可以准确测得实际位置的轨道不平顺。

以传递函数的幅值增益≮1.0为有效测量,分析弦长分别为10,30和60 m的传递函数,得到轨道不平顺波长与幅值增益的关系如图2所示。由图2可知:弦长10,30 m和60 m对应的有效测量波长范围分别为7～20,20～60 m和40～120 m。

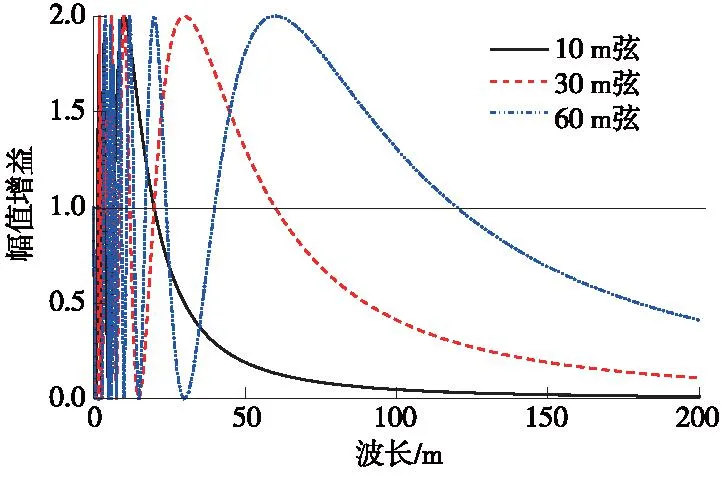
图2 中点弦测法有效波长范围Fig.2 Effective wavelength range of midpoint chord measurement method

2 超大跨度连续刚构桥

2.1 主要技术标准

设计时速:350 km。

线路情况:正线间距5 m,双线,主桥位于直线上,桥上铺设CRTS I型板式无砟轨道。

桥上荷载:桥面二期恒载140 kN/m,列车竖向荷载采用ZK活载。

设计使用年限:正常使用条件下梁体结构设计使用寿命100年。

2.2 桥梁试设计

图3为一座试设计的山区高速铁路连续刚构桥,桥跨布置为(130+250+130) m,主墩高度均为150 m,全桥总长510 m。

图3 连续刚构桥总体布置(单位:m)Fig.3 Overall layout of continuous rigid frame bridge (unit: m)

主梁:主梁为单箱单室变截面箱梁,跨中至中支点处梁高为8.5～17 m,中跨中部10 m梁段和边跨端部21 m梁段为等高梁段,其余梁段梁底下缘按二次抛物线变化。箱梁顶宽14 m,顶板厚0.6 m,中支点处局部顶板厚1.26 m,边支点处局部顶板厚1.0 m。箱梁底宽10.0 m,底板厚0.62～2.1 m。箱梁采用直腹板,腹板厚0.6 m,中支点处局部腹板厚1.5 m。箱梁各腹板上下交错设置直径为10 cm的通风孔,以降低箱内外温差。主梁典型截面布置如图4所示。

主墩:两个主墩采用H形双柱式刚架墩,均高150 m,墩顶横向宽12 m、纵向宽10 m,墩横向在梁底以下50 m范围内采用直坡,50 m以外部分墩身横向采用圆弧放坡,内外缘圆曲线半径分别为700 m和400 m;墩纵向为直坡,如图5所示。

图5 主墩构造(单位:cm)Fig.5 Main pier structure (unit: cm)

2.3 有限元分析结果

采用Midas/civil软件建立全桥模型对各施工阶段和运营阶段进行计算分析。

主梁采用C60混凝土,主墩采用C40混凝土;预应力钢束采用25-φ15.2 mm高强度低松弛钢绞线,钢绞线抗拉强度标准值为fpk=1 960 MPa。主梁、墩均采用梁单元模拟,共划分174个单元,185个节点。边界条件设置为:主梁与桥台连接设置为弹性连接(活动支座),主墩墩底固结。有限元模型如图6所示。

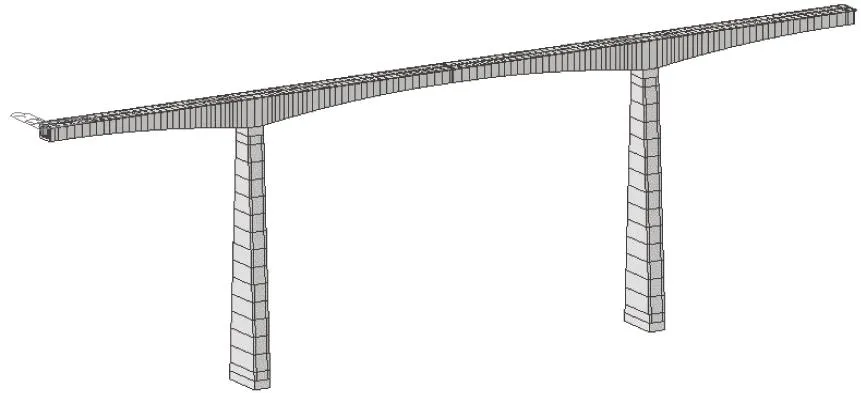
图6 连续刚构桥有限元模型Fig.6 Finite element model of continuous rigid frame bridge

按照TB 10092—2017《铁路桥涵混凝土结构设计规范》[16],分别对连续刚构主梁施工及运营阶段各项强度指标进行检算。施工阶段主梁的最大压应力为15.4 MPa,最大拉应力为0.68 MPa。运营阶段检算结果如表1所示,由表1可知,试设计的连续刚构在施工及运营两阶段的各项强度指标均满足要求。

表1 主梁应力检算汇总Tab.1 Summary of stress calculation for main beams

为确保高速行车的安全性和旅客乘坐舒适性,TB10621—2014《高速铁路设计规范》[14]对桥梁的刚度指标作了详细要求。列出本试设计主要刚度检算指标:①考虑温度与列车竖向静活载梁体最不利竖向挠跨比1/3 086(<1/1 500);②在静活载作用下最大梁端转角θ=0.61‰(<1.0‰);③在列车横向摇摆力、风力和温度的共同作用下,主跨跨中的横向位移小于主跨跨度的1/4 000,满足梁体横向变形的限值要求;④主梁徐变下挠值18.5 mm(<20 mm)。

综上所述,试设计刚构满足规范各项要求,可用于后续长波不平顺的研究。

2.4 附加变形

混凝土收缩徐变及温度效应对高墩大跨连续刚构桥的桥面附加变形的影响较为突出,其中温度效应又可细分为整体升降温及墩、梁梯度温度两种效应。本文拟采用以下方法在Midas/civil软件中分别考虑上述因素引起的桥面变形。

(1)收缩与徐变效应:连续刚构的主梁、主墩均考虑混凝土10年收缩徐变,计算模型采用CEB-FIP1990模型。

(2)整体升、降温:将本桥的整体升、降温定义为±15 ℃。

(3)梁、墩梯度温度效应:对于主梁梯度温度,《铁路桥涵混凝土结构设计规范》[16]明确给出了混凝土箱梁在竖向和横向上的梯度温度荷载;但对于桥墩梯度温度,我国相关规范并未给出明确规定。相关研究表明[17-20]:日照作用下,桥墩高度方向温度分布基本均匀,因此本文不考虑沿墩身高度方向的温差,并选取文献[17]中推荐的温度梯度函数:Ty=15.17e-7.17y(y为任一点到截面外边缘的距离)计算桥墩梯度温度。

将收缩徐变与最不利温度变形共同作用时的变形曲线相叠加,得到竖、横向最不利桥面变形。各种效应产生的桥面变形曲线如图7所示。可以发现,桥梁竖、横向的最不利变形值均出现在跨中附近,分别为59.62,9.88 mm。

图7 桥面变形曲线Fig.7 Bridge deck deformation curve

3 长波不平顺限值控制

3.1 车桥动力响应

采用“列车-线路-桥梁”动力学仿真软件开展车桥动力响应计算,相关理论见《列车-轨道-桥梁动力相互作用理论与工程应用》[21]。车辆采用CRH3型8节编组高速列车,车速取350 km/h;轨道采用CRTS-Ⅰ型板式无砟轨道;桥梁采用空间梁单元建模,各部件参数如表2所示;轨道不平顺采用德国低干扰谱模拟。

表2 桥梁模型计算参数Tab.2 Bridge model calculation parameters

为研究温度和收缩徐变效应对车桥动力响应的影响,将温度和徐变导致的横、竖向桥最不利面变形叠加到轨道不平顺中,作为等效轨道不平顺。对比两者车桥响应情况,结果如表3、表4所示。

表3 桥梁跨中处响应Tab.3 Response at the mid span of the bridge

表4 CRH3型动车组车辆响应Tab.4 Train response of CRH3

由车桥动力响应结果可知,考虑桥梁附加变形的等效不平顺后,车体竖向加速度发生显著变化,而其余指标变化不明显。说明桥梁附加变形主要影响竖桥向的行车舒适性。

3.2 合理弦长选取

首先,所选弦测长度的有效波长范围应涵盖列车的敏感波长。已有研究表明[22],高速车辆主要基频多在1 Hz左右,当以350 km/h车速行驶时,对舒适度产生不利影响的敏感波长在100 m左右。因此初步选出40,50,60 m和70 m四种弦长,对应有效波长分别为27～80,33～100,40～120 m和47～140 m。将车辆竖向振动加速度与不同弦长得到的弦测矢量值进行对比,如图8所示。可以发现:这4种弦长下的弦测值与车辆响应的匹配性总体较好,但在图中方框区域部分也有不同之处,因此需要进一步选择最优的弦测长度评价连续刚构长波不平顺。

图8 车辆竖向加速度与弦测矢量值的对比Fig.8 Comparison between train acceleration and chord measurements

将图8中各弦长测量得到的弦测结果与车体竖向加速度进行相关性分析,以选出与车体响应匹配性最优的弦测长度,结果见表5。结果表明:弦长为60 m时的测量结果相关性最优,因此建议采用60 m弦中点弦测法对连续刚构长波不平顺进行静态测量。

表5 相关系数均值Tab.5 Mean correlation coefficient

3.3 长波不平顺弦测限值

将竖向附加变形逐步放大,直至车辆响应超出限值,结果如表6所示。

表6 不同倍数桥面变形下的车辆动力响应Tab.6 Train dynamic response under different multiple bridge deck deformation conditions

可以发现:随着桥面变形逐渐增大,车辆竖向加速度和轮重减载率随之增大,且车辆竖向加速度首先超出限值。因为横桥向轨道不平顺没有改变,脱轨系数、轮轴横向力和车辆横向加速度等横桥向车桥指标无明显变化。当放大倍数为1.9时,车辆竖向加速度达到临界状态,此时的桥面变形与对应等效不平顺如图9所示。

图9 桥梁变形曲线Fig.9 Bridge deformation curve

利用弦长60 m中点弦测法分别对图9中正常状态和临界状态下的桥面变形和等效不平顺进行测量。计算时,当弦端点位于连续刚构入桥端和出桥端外侧时,对应竖向坐标y定义为0,测量结果如图10所示。由图10可知,临界状态下桥面变形对应的60 m弦最大弦测值为7.2 mm,等效不平顺对应的60 m弦最大弦测值为14.5 mm。