脉冲多普勒雷达重频参数的一种序贯估计方法

尚文秀,袁 硕,拓世英,刘章孟

(国防科技大学 电子科学学院, 湖南 长沙 410073)

0 引 言

脉冲多普勒雷达是现代电子战中的关键装备,能够实现对目标距离和速度高分辨的测量,在各国的机载预警雷达和机载火控雷达中有着广泛的应用[1-2]。例如美国F-15E“攻击鹰”上的AN/APG-63雷达、我国的歼-8Ⅱ上的射雷-8雷达、法国幻影2000-5型战斗机上的RDY型脉冲多普勒雷达、俄罗斯的苏-27上的机载РЛПК-27Э雷达等[1]。

雷达的重频参数是表征脉冲列中脉冲时序重复规律的基本参数,主要指的是脉冲重复间隔(PRI),即雷达发射一个脉冲前沿到下一个脉冲前沿之间的时间。在脉冲多普勒雷达发射脉冲列中,定义同一个波位上的发射脉冲为一个脉组,发射脉冲列由多个脉组按时序规律排列而成。为提升对杂波的抑制以及抗干扰能力,同一个脉组内一般可以划分为多个子脉组,子脉组之间采用快速切换的重频模式和参数。值得关注的是,脉冲多普勒雷达在目标检测中采用多普勒检测和相参累积的工作机制,其一个子脉组内的PRI值一般具有良好的稳定性[2-5]。脉冲重复间隔的估计是进行信号分选和PRI模式解析的首要步骤和关键流程[6-11],具有重要意义。若PRI无法得到正确的估计结果,将导致后续分选结果不准确,以及对辐射源识别方法的失败[12]。

经典的PRI估计方法主要思路是通过对截获的雷达脉冲到达时间(TOA)序列进行差分处理,得到达到时间差(DTOA)序列,再进行统计或搜索分析。基于PRI统计直方图分析的时差累积直方图方法(CDIF)[10]和改进的顺序直方图方法(SDIF)[13],主要流程是计算多阶DTOA并以直方图的形式进行统计,最后设置门限,从直方图中提取PRI值;PRI变换法采用谱变换的方法,将建模后的脉冲列变换为PRI谱,对脉冲列中的PRI整数倍谐波有较好的抑制作用[14];PRI平面变换法是将TOA序列按一定方式投射到二维空间,再利用平面处理的方式对PRI进行估计[15]。上述传统的离线参数估计,大多在接收比较完整的脉冲列之后进行,对脉冲列整体采用搜索、统计等方法来提取重频信息。这类方法往往需要大批的数据积累,不能适应高密度的数据流,难以满足数据处理实时性的要求。在无源雷达信号处理领域,截获数据流密度大[16]、数据处理时效要求高是电子侦察数据处理算法面临的主要问题[17]。序贯处理的机制符合处理脉冲流数据的特点,脉冲多普勒雷达重频参数的序贯估计符合提高电子侦察实时性的发展趋势。

本文针对逐脉冲序贯重频参数估计的场景,引入了评估变量控制对脉冲的缓存,对受漏脉冲和干扰脉冲等数据噪声污染的脉冲列进行了较高精度的参数估计;进一步对缓存区间内的脉冲采用试探整除的方法,对脉冲多普勒雷达截获脉冲列中重频切换的跳变时刻进行了跟踪检测。

1 问题描述

1.1 脉冲多普勒雷达脉冲序列模型

重频参数的选择决定了脉冲多普勒雷达的测距能力和对目标接近速率的测算能力,为实现解模糊的需求,目前大多数脉冲多普勒雷达采用的是多个PRI联合切换的方式[2],依据实际观测目标对解模糊的需求来切换PRI不同的子脉组,以减少距离和多普勒盲区。其在目标检测中需要提高信噪比,需要对同一PRI进行相参积累,以同一PRI发射一串序列。综合上述两个特点,脉冲多普勒雷达发射脉冲列中PRI采用子脉组捷变的调制方式[18]。

一个脉组由几个PRI不同(参差)的子脉组按时序排列成,则一个脉组中PRI序列P为

(1)

式中：p1,p2,…,pk表示每个子脉组内的重频值;n1,n2,…,nk表示每个子脉组内包含的重频间隔数;k表示脉组中存在的子脉组数目。

图1展示了脉冲多普勒雷达脉冲列中脉组和子脉组的层次结构。

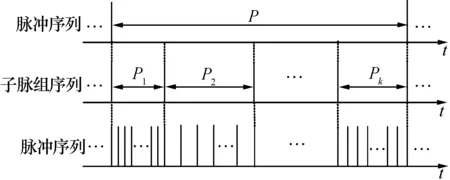
图1 脉冲多普勒雷达脉冲列结构

图2 包含漏脉冲和干扰脉冲的脉冲列

图3 仿真场景下DTOA与PRI相比的偏差

设接收机截获到一个包含N+1个脉冲的脉冲列,其到达时间序列可表示为

T={t0,t1,t2,…,tN}

(2)

将式(1)中N+1个脉冲构成的TOA序列做差分计算,可以得到包含N个DTOA的序列τ。

τ={d1,d2,…,dN}

(3)

式中：di=ti-ti-1,i=1,2,…,N。

对于理想条件下截获的雷达脉冲列,TOA序列直接做差分得到的DTOA序列在数值上同脉冲重复间隔(PRI)序列相同。在实际的电子侦察场景中,接收雷达脉冲是非合作的,截获的脉冲列与原始雷达发射脉冲列并不完全相同,存在着大量数据噪声等干扰情况,直接对TOA序列差分所得到的DTOA序列不能直接作为真实的PRI序列。观测到的DTOA序列在真实重频序列的基础上增加了数据噪声造成的偏差,但DTOA序列中仍然蕴藏着与原本PRI序列相关的大量信息,重频参数估计的一种思路就是从DTOA序列中提取出真实的重频值序列。

1.2 重频参数估计问题及非理想因素的影响

传统的重频参数估计方法主要适用于离线分析的场景,即对足够长的静态脉冲列进行统计、搜索等分析,从而对PRI序列进行整体估计。

(4)

离线处理方法一般输入为静态的截获脉冲列的TOA序列差分得到的DTOA序列,输出为PRI的估计结果序列。整个过程中需要对整个脉冲列进行反复搜索,对整个脉冲列的信息以及PRI序列的整体估计结果统一进行考虑。

序贯重频参数估计方法同样是利用截获的DTOA序列进行分析,但是序贯参数估计的过程是随着脉冲被截获的过程进行的,每次序贯参数估计的过程,只考虑输出当前截获脉冲对应的重频参数值,输入为当前累积截获的DTOA序列。

(5)

式(5)表示对第i个重频参数值进行估计的过程,其中τi={d1,d2,…,di},表示目前已接收脉冲列中获得的DTOA序列。在序贯估计的过程中,重点关注当前新到达脉冲的估计结果。

电子侦察过程中,可能由于目标信号强度较低,或者接收机只接收到了目标信号的副瓣方向,导致部分脉冲被噪声淹没,形成漏脉冲的现象。此外,来自其他雷达辐射源的脉冲会以干扰脉冲形式混杂在脉冲列中。漏脉冲和干扰脉冲会破坏脉冲列的结构和脉冲列中的时序规律,加大了重频参数估计的难度。如图 2所示为漏脉冲和干扰脉冲在脉冲列中的存在形式,其中线段为正常脉冲,阴影方框为漏脉冲,黑色方框为干扰脉冲。

图 3展示了漏脉冲率为20%,干扰脉冲率为20%时实际仿真场景下观测到的DTOA序列与真实PRI序列之间的对比情况,可见在漏脉冲和干扰脉冲等因素的干扰下,DTOA序列相较于真实PRI序列存在很大的偏差,但整体趋势上还是随着真实PRI值的变化而波动。

1.3 重频跳变时刻估计及非理想因素的影响

脉冲多普勒雷达发射脉冲列中,一个脉组内一般进行解模糊的设计,分为多个重频值不同的子脉组,相邻子脉组之间重频参数一般没有特殊的数值关系(例如相等、倍数等)。

定义跳变时刻为完整脉冲列中重频参数发生跳变的时刻,在该时刻前后重频参数发生突变,子脉组发生切换,如式(6)所示。

th={t||pt1>t-pt2≤t|>ε}

(6)

在完整无噪声的脉冲列中,跳变时刻为一个子脉组中最后一个尾脉冲前沿对应的时刻。但在存在漏脉冲以及干扰脉冲分裂原有脉冲重复间隔的情况下,尾脉冲可能被遗漏,或者会因为干扰脉冲的影响而被混淆,但是跳变时刻的性质保持不变。

图4展示了漏脉冲和干扰脉冲都为20%,真实仿真场景下重频跳变时刻在序列中的位置,图4a)为理想情况下跳变时刻的位置,图4b)为实际仿真中跳变时刻的位置。

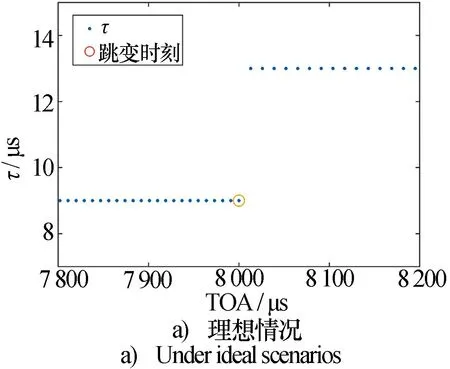
图4 不同场景下跳变时刻在DTOA和PRI序列中的位置

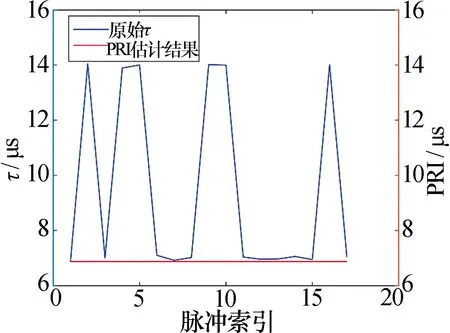
图5 直线拟合法处理效果

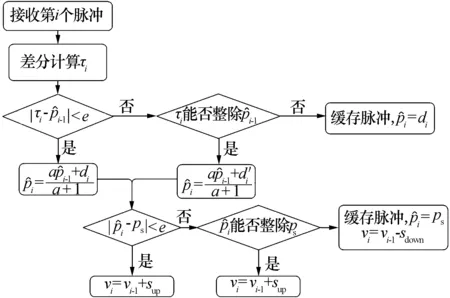
图6 序贯估计重频参数的方法流程

在理想环境中,跳变时刻表现为前一个子脉组的最后一个脉冲所在的时刻,而在加入漏脉冲和干扰脉冲后,跳变时刻不存在于原有的TOA序列中。原有的跳变时刻两侧的脉冲间隔被掺杂的噪声信息所掩盖,前后两个子脉组之间也失去了原本明显的区分特征,在重频切换处不稳定的DTOA波动就会增加对跳变时刻估计的困难。

2 常规估计方法和局限

传统的脉冲重复间隔估计方法主要有两大类,一类是基于占比统计的方法,一类是基于脉冲列中脉冲的连续性特性的方法。

基于占比统计的PRI估计方法通过计算脉冲序列的脉冲间隔进行分类统计,搜索其中占比最高且满足一定门限要求的脉冲间隔作为可能的PRI,例如基于统计直方图统计的CDIF[10]和SDIF[13]、PRI聚类法[19]、PRI变换法[14]以及其他相关的改进方法等。实际工程中考虑到脉冲丢失和外界杂乱脉冲干扰的影响,通常会进行多级的脉冲间隔计算。

基于连续特性的PRI估计方法搜索脉冲序列中脉冲间隔相等的多个连续脉冲(至少3个以上),并以其为基准继续搜索其他脉冲间隔相等(或满足倍数关系)的脉冲,如果搜索到的脉冲数满足门限要求则认为该基准的脉冲间隔为估计所得到的PRI,例如直接序列搜索法[20]、动态关联法等。

以上方法主要适用的场景是在离线处理的情况下,在对脉冲列数据有大量的积累之后,再对数据整体进行统计处理,如果面临序贯处理的场景,会在实时接收的过程中对获得的数据进行多次统计,造成对数据的重复搜索,对信息的利用率较低,冗余计算量大。而且在序贯场景下,在未能获取到有相对完整的重频结构的脉冲列之前,获取的信息可能很有限,则脉冲之间的相关性较弱,常规的传统方法很难进行有效的关联搜索,而可能受残缺的脉冲列信息引导而导致处理的结果偏差较大。

以直线拟合法为例,对于子脉组参差的脉冲列,重频参数在同一子脉组内是数值基本不变的状态量,而DTOA序列的数值在以重频参数为基础而产生偏差。对同一子脉组内的DTOA值做一阶回归处理进行直线拟合,可以获得一个对重频值的估计结果。

τ=p+a(t)

(7)

式中：τ为观测到的DTOA序列;a(t)为由于数据噪声和漏干脉冲因素在DTOA序列造成的偏差序列。

在同一子脉组内p为固定值,漏脉冲和干扰脉冲在序列中是随机出现的,对同一子脉组内的DTOA序列进行一阶直线拟合,即可对当前的PRI值进行估计。

(8)

对DTOA序列做回归处理后的数值集中在一条直线上,在同一子脉组内取中位数作为重频参数的估计值。当回归直线的斜率k大于阈值时,判断为重频发生切换。

图 5展示了直线拟合法对同一子脉组内的DTOA序列进行直线拟合估计的效果,其中对于漏脉冲造成的对PRI成倍数的特殊情况,进行了去除倍数的处理,将其归简为去除倍数的值后再参与拟合。

但这种方法在漏脉冲和干扰脉冲比例较大的情况下估计结果的偏差较大,同时对重频切换的时刻反应不灵敏。

3 脉冲多普勒雷达重频参数的序贯估计方法

3.1 重频参数估计

序贯重频估计的过程可以建模为一个函数的形式,函数的输入是前一个脉冲重频值的估计结果和当前观测到的DTOA值,输出为当前对重频值的估计结果。

(9)

(10)

定义变量v为对每次重频估计值的估计结果做出评估的评估变量。在序贯估计的场景下,每次估计后的得到的参数估计结果只是一个临时结果,随着接收脉冲列的积累,后续可能对当前结果进行一定的修正和调整。因为无论是当前观测到的DTOA值还是当前重频的估计结果,都受短时间内脉冲列提供信息的影响较大,变量可以将当前的估计结果与估计的子脉组的驻留PRI进行比较,从而对当前估计结果进行评估。

(11)

函数g(·)表示评估变量随接收脉冲自我更新的函数,具体如式(12)所示：

(12)

式中：ps为当前子脉组驻留PRI的估计值。

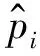
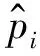
(13)

v只在vmax和vmin之间变化,超过vmax时,v将不再增大;超过vmin时,v不再减小。

Δv=vmax-vmin=nsup=msdown

(14)

式(14)表示了评估变量v在变化过程中涉及到的参数关系,其中n,m分别控制在评估估计结果时有效作用脉冲的个数,累积超过该个数,评估变量会分别到达边界。vi=vmax时,表示当前脉冲的位置处于子脉组内部;vi=vmin时,表示当前脉冲的位置处于相邻子脉组切换的交界处。Δv是评价变量v的变化范围,为预设参数。

在图 6中,评估变量不仅能实时指示当前重频估计结果的可信任程度,而且在估计过程中可以作为一个记录脉冲列中信息变化的变量,从而将已接收的脉冲列中对重频估计有用的信息及时保存,并作用于对新接收脉冲重频的估计中,这样就在避免每次接收脉冲都要进行大量对脉冲列的重新搜索,提高了对脉冲列中信息的利用效率。

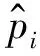
3.2 跳变时刻估计

在脉冲列中重频发生切换时,重频参数会出现跳变,在跳变后DTOA序列也会因重频参数的切换而表现出与跳变前不同的规律。但是在加入漏脉冲和干扰脉冲的情况下,如果在发生重频切换的时刻附近出现了脉冲的异常,就难以精确地定位前一个子脉组的尾脉冲和后一个子脉组的首脉冲。如图 7所示,图7a)、图7b)分别为在重频切换处出现漏脉冲和干扰脉冲情况下对跳变时刻估计产生的影响。

图7 重频切换处漏脉冲与干扰脉冲的影响

在出现干扰脉冲或者重频切换的情况下,检测到的DTOA是与之前的重频估计结果没有明显数值关系的奇异值,此时采取的处理方式是对脉冲进行缓存处理。这样的缓存区间就存在于子脉组内部的干扰脉冲处,或是子脉组之间的重频切换处。子脉组内的干扰脉冲一般是随机产生的,不符合重频时序规律,也没有与其他脉冲之间的信息联系,一般在短时间内的信息积累就可以剔除单个干扰脉冲的影响。但在重频切换处,评估变量v会经历从vmax减小到vmin、再重新增大到vmax的过程,在这个时间区间内的脉冲被暂时缓存,通过比较脉冲缓存前后重频值发生的变化,可以确定重频切换时刻位于缓存区间内,从而再从该时间区间内进一步分析确定重频值跳变时刻。

通过对重频参数的估计,切换前后稳定的估计值所处的脉冲之间可以确定发生重频切换的时间区间D。

D=te-ts

(15)

式中：te为当前v=vmax时的脉冲到达时间,即确定已经发生了重频切换的具有新的重频参数的脉冲处;ts为从te开始逆时序检测到的第一个除te之外满足v=vmax的脉冲的到达时间。

D=nipi+njpj

(16)

该段时间区间由切换前后的重频pi,pj组成,通过对式(16)求解出整数ni和nj,就可以将该段时间区间内的重频结构进行重构,将由异常的干扰情况造成的对脉冲列中重频结构破坏的影响尽可能降低。

在重频切换处存在干扰脉冲时,在上一个子脉组的尾脉冲之前,会使得检测到的脉冲间隔发生点提前,在前一个子脉组的尾脉冲之后,不影响对重频切换时间区间的起始时间的判断。但需要注意的是,由于干扰脉冲破坏了子脉组中稳定的脉冲信息,集中的干扰脉冲可能影响对当前脉冲列位置状态判断,干扰到对跳变时刻的估计。

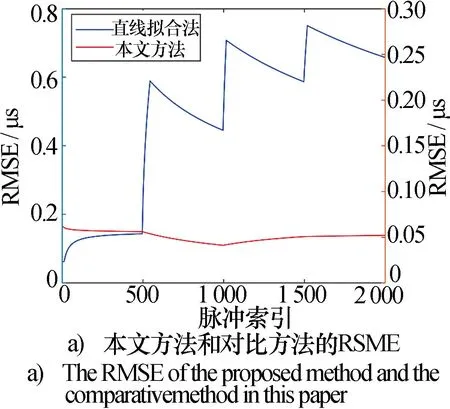
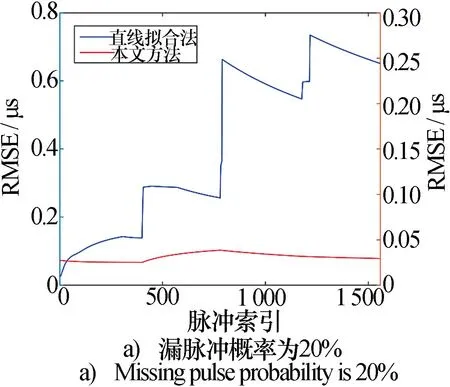
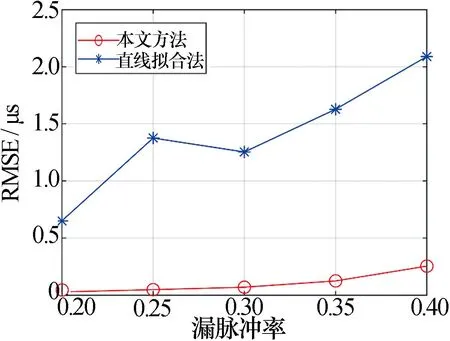
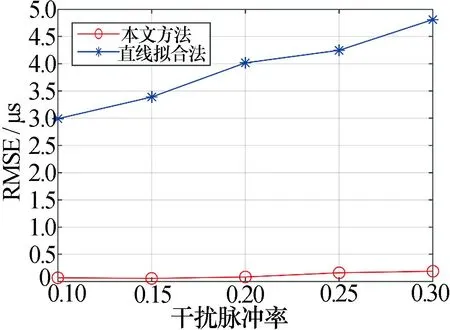
对时间区间D内的重频结构进行重建的过程,可以视为对D进行关于因数为pi和pj的整数分解,分解的结果必定有解。不妨设i

(17)

依次计算D-spi能否整除pj,可以整除时得到ni和nj的解。在求解得到ni和nj后可以估计跳变时刻为

th=ts+ni×Psi

(18)

4 仿真实验

4.1 实验设置

仿真实验设置一组重频按子脉组参差的脉冲列,通过加入不同比例的漏脉冲、干扰脉冲等噪声来模拟实际接收状况,实验以序贯接收过程中重频参数的实时估计效果为主要观测对象,通过记录过程中的估计准确率、参数估计结果的精度以及跳变时刻的估计精度等指标,说明本方法在序贯参数估计中的效果。

实验设置的脉冲串以[7μs×500, 9μs×500, 13 μs×500, 17 μs×500]的重频参数规律生成,其中数组中前一个数字为PRI的值;后一个数字为该子脉组中脉冲数量,因此上述原始脉冲串总长为2 000个脉冲,在此基础上随机加入漏脉冲和干扰脉冲。在仿真实验中为模拟序贯处理的条件,将脉冲串按逐脉冲读取的方式读入算法中,在每一次读入脉冲处理后输出一次重频参数的估计结果。

4.2 结果分析

本文主要分别验证在脉冲列中加入漏脉冲、干扰脉冲等干扰噪声后,测试算法估计重频参数以及估计跳变时刻的性能,选择直线拟合法作为仿真实验的对比方法。

4.2.1 对数据噪声的适应性能测试实验

本实验中在脉冲列中加入标准差为0.04 μs的白噪声,分别用本文方法和对比方法进行估计,估计结果的均方根误差随脉冲接收时间变化如图8a)所示。

图8 加入数据噪声后的实验结果

由于在重频切换的时间跳变点处,直线拟合法会存在一定的时间延迟,因此图8a)中估计精度也会在跳变时刻处有较大偏差,而在不存在干扰脉冲和漏脉冲的情况下,本文方法可以找到跳变时刻的脉冲从而找到精确的跳变时刻,因此所得的估计结果误差较小。

图8b)为直线拟合法估计的重频参数值与真实值的对比结果,可以观察到在发生重频切换的时候,直线拟合法有明显的时间延迟。

4.2.2 对漏脉冲的适应性能测试实验

本实验中在脉冲列中加入标准差为0.04 μs的白噪声,在此基础上再分别随机按20%、30%、40%的比例对原始脉冲列中的脉冲进行丢失,再分别用本文方法和对比方法进行估计,估计结果的均方根误差随接收脉冲数目变化分别如图9a)、9b)、9c)所示。

图9 存在漏脉冲时的实验结果

图9中展示的实验结果表明,在序贯接收脉冲的过程中,本文方法始终对漏脉冲具有较好的适应性,可以保持较好的估计精度,而且呈现出明显的分段趋势,跳变时刻明显。对比方法在序贯接收脉冲的过程中受漏脉冲影响,出现了大量错误估计的结果,且分段特征模糊,对跳变时刻的估计出现了大量虚警。

图10展示了在不同漏脉冲率场景下本文方法估计结果的均方根误差与直线拟合法估计结果均方根误差的对比。由表1可以得知,本文的方法对漏脉冲的适应能力较好,在40%漏脉冲率的情况下还可以达到均方根误差在0.25 μs以下的估计精度,而对比方法估计结果的均方根误差达2 μs以上,本文方法估计效果明显好于对比方法。

表1 存在漏脉冲时跳变时刻的估计误差

图10 不同漏脉冲率场景下估计结果的RSME

仿真脉冲列中存在三个重频切换跳变的时刻,分别为t=[3 500 μs, 8 000 μs, 14 500 μs]三个时刻,将跳变时刻的估计结果与这三个时刻的作差,即可得到跳变时刻估计结果的误差。表1展示了在各自漏脉冲场景下在对跳变时刻的估计结果,三个结果误差均不超过0.04 μs,在数据噪声偏差之内准确找到了跳变时刻,估计性能较好。

4.2.3 对干扰脉冲的适应性能测试实验

本实验中在脉冲列中加入标准差为0.04 μs的白噪声,在此基础上再分别随机按20%、30%、40%的比例在原始脉冲列中随即加入干扰脉冲,再分别用本文方法和对比方法进行估计,估计结果的均方根误差随脉冲接收数目变化分别如图11a)、11b)、11c)所示。

图11 存在干扰脉冲时的实验结果

图11中展示的实验结果表明,在序贯接收脉冲的过程中,本文方法始终对干扰脉冲具有较好的适应性,可以保持较好的估计精度,而且呈现出明显的分段趋势,跳变时刻明显。对比方法在序贯接收脉冲的过程中受干扰脉冲影响较大,出现了大量错误估计的结果,几乎完全丧失了原始脉冲列的分段特征,对跳变时刻的估计出现了大量虚警。这是由于干扰脉冲对于脉冲列的结构破坏的程度更大,对估计结果的影响更大,在直线拟合法无法剔除大量存在的干扰脉冲增多造成的无规律的野值,导致估计的偏差越来越大,而本文方法有效适应了这种影响。

图12展示了在不同干扰脉冲率场景下本文方法估计结果的均方根误差与直线拟合法估计结果均方根误差的对比。由表2可以得知,本文的方法对干扰脉冲的适应能力较好,在30%干扰脉冲率的情况下还可以达到均方根误差在0.25 μs以下的估计精度,而对比方法估计结果的均方根误差达4.5 μs以上,本文方法估计效果明显好于对比方法。

表2 存在干扰脉冲时跳变时刻的估计误差

图12 不同干扰脉冲率场景下估计结果的RSME

表2为干扰脉冲率为10%、20%、30%时对跳变时刻的估计误差,其误差计算方法与表 1相同,随着干扰脉冲率的增大,本文方法对跳变时刻的估计性能有所下降,但仍能保持在百微秒量级,即十个脉冲左右的误差区间。

5 结束语

本文针对脉冲多普勒雷达脉冲列重频参数序贯估计问题,着重考虑漏脉冲、干扰脉冲等数据噪声对重频值估计精度和跳变时刻估计精度的影响,引入了评估变量控制对脉冲缓存的方法。仿真实验表明,在不同数据噪声的实验条件下,本文方法对截获脉冲列中重频参数的序贯估计的精度和对跳变时刻的估计精度优于传统重频估计方法。在漏脉冲率不高于40%的情况下和干扰脉冲率不高于30%的情况下,本文方法对重频值的估计RMSE均可以保持在0.25 μs以下,对跳变时刻的估计误差在10个脉冲以内。