基于电磁计算的同时极化雷达成像仿真

陈 云,张云华*,李 东

(1. 中国科学院国家空间科学中心 微波遥感技术重点实验室, 北京 100190) (2. 中国科学院大学 电子电气与通信工程学院, 北京 100049)

0 引 言

极化雷达技术的发展丰富了雷达目标特征信息,形成各种新体制雷达更好地满足目标高分辨检测、成像、抗干扰、分类与识别等需求[1]。准确获取以极化散射矩阵为代表的目标极化散射特性是极化雷达技术研究的重要内容,通常可采用分时极化和同时极化测量体制雷达获取目标的极化散射矩阵[2-4]。所谓分时极化测量,是指雷达交替发射水平和垂直极化波形,同时接收两种极化的回波信号;在该种体制下,以实际的脉冲雷达为例,至少需要发射水平极化和垂直极化两个脉冲信号才能获得极化散射矩阵的全部四个元素,因此目标运动去相关会对测量结果造成影响。而同时极化测量体制则是同时发射水平极化和垂直极化的雷达信号并同时接收两种极化的回波信号,这样只需发射一个脉冲信号便可获得目标的极化散射矩阵,可降低目标运动对极化散射矩阵测量的影响[5-6]。1993年,文献[2]提出使用了一对具有相反斜率的线性频率调制(LFM)信号实现同时极化测量。文献[3]针对经典极化学中“时谐性”或者“窄带性”约束条件的局限性提出瞬态极化概念。2019年,文献[7]将随机信号与极化技术结合提出随机极化新型探测技术,将信号的随机性由最初的时、频域拓展至极化域,降低波形的极化度,使得雷达具有更好的低截获性能,其核心思想均是在两正交极化通道上同时发射两路平均功率相等的正交随机波形。

雷达信号的模拟仿真是目标散射特性和雷达技术研究与发展的重要方面,尤其对于新体制雷达技术的研究具有重要价值,而雷达信号的电磁(EM)仿真可以获得更加接近于实际的雷达回波信号,因而备受关注[8-10]。在雷达系统的研发或者对某一特定目标EM场特性的研究过程中,开展现场实验和暗室测量不仅EM环境难以控制,而且过程复杂,成本较高;通过建立回波信号仿真模型,实现雷达目标回波信号的仿真,不仅在雷达系统的设计过程中至关重要,而且对数据进行进一步处理也发挥重要作用[11-12]。复杂目标的极化散射特性因包含各种散射机制难以通过点目标回波模型表示,其与真实目标的回波差异较大,不足以满足当今新体制雷达研究需求[13];解决这个问题的一个很好的方法是通过EM计算工具(例如FEKO、HFSS或XFDTD)建立一个EM仿真模型较为精细地反映目标的散射特性,但必须指出的是这些工具不能直接获取雷达目标时域回波信号[14-16],特别是基于目标散射特性的同时极化雷达目标回波仿真研究,尚未看到相关报道,因此,深入探究同时极化雷达目标回波仿真方法具有深远的研究意义。

本文提出了一种基于EM计算的同时极化雷达(SPR)成像仿真方法。首先,基于FEKO建立目标的几何模型,根据目标电尺寸等因素选择合适的频率步长构建目标全空间全极化宽带EM散射特性数据库[17];并采用完全互补序列(CCS)[18-19]设计正交性良好的低旁瓣同时极化波形; 然后,根据目标相对雷达视线的姿态角对数据库进行插值调用,将同时极化发射信号与插值调用的极化散射数据进一步处理得到目标的时域回波信号。以F22为例进行了同时极化雷达的回波EM仿真,进而得到雷达图像,并进行了Pauli分解及幅相误差影响分析。该方法同时适用于其它体制、其它波形的回波仿真,对开展新体制雷达系统幅相特性、波形性能等研究具有重要的意义。

1 SPR回波信号模型及仿真方法

SPR系统如图1所示,在不考虑雷达系统非理想因素的情况下,假设sH(t)、sV(t)分别表示同时极化雷达H极化通道和V极化通道的基带信号,雷达发射信号可以表示为

(1)

图1 SPR系统框图

式中：Tp为脉冲宽度;t为时间变量,0≤t≤Tp;fc为载波频率;h和v分别为单位水平和垂直极化基; Rect(·)为矩形函数。

因此,发射信号的频谱可以表示为

(2)

对于单个点目标的情况下,设雷达与点目标之间的距离为R(t),点目标的径向速度为v(t),忽略EM波传播过程中的能量损失,则点目标的射频回波可以表示为

(3)

式中：β=(c-v(t))/(c+v(t))为缩放因子,表征目标速度对雷达波形进行了尺度调制;c为电磁波的传播速度;τ为回波的时延。此时,可将雷达发射波与点目标的相互作用视为线性系统响应,当目标静止时,系统函数为冲击响应函数。

针对具有复杂EM极化散射特性的目标,可以将其极化散射特性看作系统响应函数h(t)。SPR射频回波信号可表示为

(4)

式中：“*”表示卷积。由傅里叶变换的性质,可将h和v正交极化基下,复杂目标射频回波信号对应的频谱表示为

exp(-j2πfτ)

(5)

其中

为目标的EM极化散射特性,可以通过利用EM仿真工具计算获取。因此,由傅里叶变换关系可将复杂目标的基带回波信号表示为

(6)

进一步考虑雷达系统的非理想特性,目标的测量散射矩阵M可以写为

(7)

式中：f1和f2为极化通道的不平衡项;δi,i=1～4为雷达系统的串扰项;Nij(i,j为h或v)为各通道的附加噪声项。同时极化雷达目标成像仿真流程如图2所示,具体步骤如下：

图2 SPR目标成像仿真流程

(2) 同时极化雷达波形设计。设计同时极化雷达波形sH(t)、sV(t),并引入发射通道非理想特性生成同时极化发射信号e(t)。

(3) 径向运动对波形尺度调制后为e(βt),其中尺度调制可通过变采样率实现,最后对e(βt)进行傅里叶变换得到G(f)=E(f/β)。

(4) 叠加目标EM极化散射特性并添加时延分量得到回波信号频谱：R(f)=H(f)G(f)e-j2πfτ。

(5) 引入接收通道非理想特性后进行逆傅里叶变换,并模拟接收机热噪声,产生噪声干扰下的目标回波,得到最终的时域回波信号

(8)

式中：n(t)为按照设定的信噪比(SNR)添加的高斯噪声。

上述SPR目标回波仿真过程中,目标极化散射特性数据库的构建只需依据目标的尺寸利用FEKO对较少的频率采样点进行EM计算,可以极大地减少EM散射计算量。

2 SPR波形设计

可用于SPR的常用正交雷达波形主要包括：“正负斜率LFM波形”、“正负斜率非LFM波形”、“正交多相编码波形”等[20]。LFM信号脉冲压缩后峰值旁瓣电平(PSL)为-13.26 dB。自适应滤波、加窗及其它技术可用于改善LFM波形的PSL;然而,这些方法将导致SNR损失和主瓣展宽[21];此外,通过驻定相位原理可以证明LFM信号的正交性受时间带宽积的限制[22]。相位编码波形具有较高的设计自由度,特别是CCS具有理想的相关特性,可用于产生正交性和旁瓣特性良好的SPR信号。本文基于优化最小化(MM)方法,采用CCS设计SPR波形[17],其波形可以表示为

(9)

式中：u1(n),u2(n)表示由CCS相位编码;tb为码元宽度;L为序列的码长。假设雷达一个相关处理周期包含K个长度为N的恒模相位编码,占空比为d,整个脉冲宽度为T=KNtb/d=Ltb/d。一对正交CCS可表示为

(10)

(11)

其中

(12)

可以将p1、p2视为(K,N)的CCS,K为脉冲数,N为序列长度。任意两个CCS在滞后处的非周期性互相关可以定义为

i,j=1,2,k=1,…,K,n=0,… ,N-1

(13)

当i=j时,式(13)变为CCS的自相关函数。

为了设计具有良好自相关和互相关的序列,以互补积分旁瓣电平(CISL), 即自相关函数的旁瓣能量与互相关函数加权能量之和为代价函数,考虑如下优化问题

(14)

式中：ωn=ω-n≥0,n=0,…,N-1为不同时延的非负加权因子。优化问题式(14)中目标函数为非凸问题,由于序列采用互补结构,并且同时考虑了序列的自相关与互相关特性的优化,文献[19]中提出的用于设计恒模单脉冲序列的积分旁瓣电平最小化算法不能被直接应用。针对优化问题式(14),令L=K(2N-1),并定义一个长度为2L的辅助序列

(15)

(16)

式中：vec(·)表示矩阵的矢量化;Un,n=1-L,…,L-1是L×L的Toeplitz矩阵,即

i,j=1,…,L-1

(17)

通过利用式(16),令Z=zzH,优化问题式(14)可以被重写为

min vec(Z)HLvec(Z)-2ω0N2K2,
s.t. |z(n)|=1,n=1,…,2L

(18)

其中

(19)

由于ωk≥0,很容易发现为L非负的实对称矩阵,且满足Hermitian矩阵要求,因此可以利用MM方法处理优化问题 式(18),同时达到对序列的自相关函数与互相关函数优化。

3 仿真试验

为了验证本文同时极化雷达目标成像仿真的有效性,选取图3所示F22飞机(机长10.8 m、翼宽7.9 m、高度2.3 m),利用EM计算工具FEKO建立逆合成孔径雷达(ISAR)转台模型。为了避免引起距离模糊,频率步长需满足Δf≤c/2E,其中E为目标的距离范围。因此,以频率步长Δf=0.01 GHz,Δθ(俯仰)=Δφ(方位)=1°,构建目标在0.8 GHz～1.8 GHz频段的全空间全极化散射特性数据库。图4为目标在频率为1.3 GHz处的全空间全极化RCS电磁散射特性。

图3 F22三维模型

图4 F22模型全空间、全极化RCS特性(f =1.3 GHz)

设定发射的同时极化波形的载频、脉宽和带宽分别为Tp=10 μs,fc=1.3 GHz,B=280 MHz,采用本文所提出的方法设计码长N=420、脉冲数K=5的CCS同时极化波形。波形如图5所示,其自相关函数旁瓣和互相关函数均能达到-100 dB。

图5 同时极化波形

(1) 同时极化雷达成像仿真

利用前面的仿真方法“装配”了F22模型俯仰角θ=0°,方位角φ=-180°～180°,Δφ=1°的回波信号,仿真SNR为30 dB,暂不考虑雷达系统的非理想特性。图6为目标回波信号进行匹配滤波后的一维距离像(HRRP);其中图6a)～图6d)为发射正负斜率LFM同时极化波时得到的HH、HV、VH和VV四个极化通道的HRRP,图6e)～图6h)为发射正交CCS同时极化波时对应四个极化通道的HRRP。很明显,相比于正负斜率LFM,所设计的CCS同时极化波形有更好的旁瓣抑制。

图6 不同的SPR波形下F22 HRRP仿真对比

图7给出了基于BP算法的ISAR成像结果,两种波形的成像结果均表明同极化HH、VV通道的图像轮廓清晰,尤其是头部和飞机尾部具有更强的散射强度。另外,由于水平机翼较薄,其边缘呈现水平偶极子特性,在HH极化通道中所产生的一次散射比VV通道中更强。垂直机翼边缘在HH、VV极化中表现为弱散射体,在正负斜率LFM同时极化波中,由于波形具有较高的距离旁瓣,垂直机翼被尾部强散射体掩盖, 而在CCS同时极化波中,由于波形良好的旁瓣特性从而可以清晰呈现垂直机翼。对于交叉极化图像,强散射主要来自进气孔、垂直机翼边缘和尾部等复杂散射机制。但是,值得注意的是相同的图像动态范围内,图7b)和图7c) 中可发现水平机翼后边缘存在交叉极化散射,而图7f)和图7g)中几乎没有出现。该差异进一步说明相比于正负斜率LFM波形,所设计的正交CCS同时极化波还具有更好的波形正交性,能精确获取目标的极化散射矩阵。上述两种波形的回波信号均体现了丰富的目标极化散射信息,而且回波信号的处理结果也反映了波形的性能差异,表明了本文所提出的同时极化雷达目标成像仿真方法具有较高的精度。

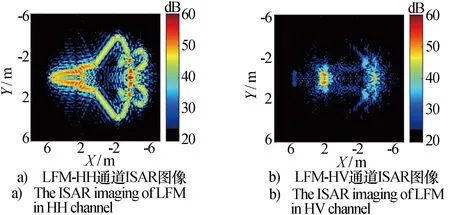
图7 不同的同时极化雷达波形下F22 ISAR成像仿真对比

(2) 极化通道非理想特性仿真

由极化散射矩阵可以获得与目标有关的极化信息,前面的分析没有考虑极化通道非理想特性,非理想特性的引入会影响极化散射矩阵的测量,并可能导致目标散射特性和结构信息的解译错误。本节利用所建立的仿真平台就极化通道的非理想特性对极化散射信息提取的影响进行EM仿真。发射波形采用所设计的正交CCS同时极化波形,假设已使用文献[23]中描述的方法进行了系统校准,但是残余的通道非理想特性仍然存在。进一步假定互易系统在收发通道上有相同的非理想特性,残余的通道非理想特性影响针对以下三种情况下进行回波仿真：(1) 相位不平衡为Δφ=0°时,幅度不平衡从0到5dB变化;(2) 幅度不平衡为0 dB时, 相位不平衡arg{f1}=arg{f1}=Δφ从0°到180°变化;(3) 幅度不平衡为0 dB,相位不平衡Δφ=0°时,雷达系统串扰δi,i=1～4从-10 dB～-30 dB变化。图8给出了不同非理想特性条件下CCS同时极化ISAR成像后Pauli分解[1]的结果,其图像具有红色R=|SHH-SVV|、绿色G=|SHV+SVH|和蓝色B=|SHH+SVV|颜色编码。

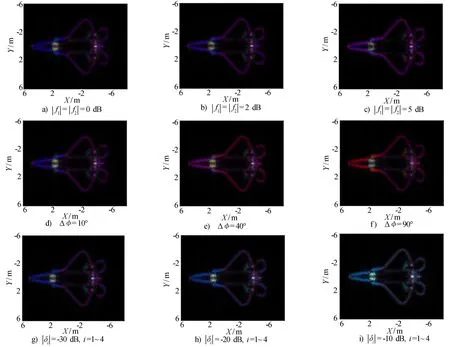
图8 极化通道非理想特性下Pauli分解结果

图8a)～图8c)为幅度不平衡特性的影响,可以发现Pauli分解结果对雷达系统的幅度不平衡有较高的容忍性,2 dB范围内的幅度不平衡几乎不影响Pauli分解结果;机头、座舱边缘表现为蓝色的一次散射机制,而较薄的水平机翼导致HH通道中的一次散射比VV通道中更强,类似于奇次散射和偶次散射的组合呈紫色。进气孔为腔体形式散射机制复杂,等效相位中心发生偏离,呈现绿色的体散射形式。每种颜色的色调实际上表示了每种散射机制的能量贡献。图8d)～图8f) 展现了极化通道相位不平衡特性的影响,10°范围内的相位不平衡几乎不影响Pauli分解结果;当收发通道的相位不平衡达到90°时,蓝色的一次散射机制被解译为红色的二次散射机制。图8g)～图8i) 展现了极化通道串扰的影响,可发现-30 dB以下的极化串扰几乎不影响Pauli分解结果;当极化串扰达到-10 dB时,目标散射机制发生很大的变化,会有多种散射机制的叠加,对目标极化信息的解译产生很大的影响。

4 结束语

本文在推导SPR目标回波信号模型的基础上,提出了基于EM计算的SPR目标成像仿真方法,初步建立了可为SPR技术研究提供高保真EM仿真的平台。工作表明,基于CCS设计的波形可很好地满足SPR的应用需求。通过利用EM计算工具FEKO构建目标全空间全极化散射特性数据库,然后基于MM方法设计CCS同时极化发射信号,引入雷达系统的非理想特性,将同时极化发射信号与调用的散射特性数据进一步处理得到目标高保真回波信号。对仿真实验的结果分析表明基于EM计算的目标成像较理想点目标模型更能反映目标EM散射的真实情况,在相同的雷达系统参数条件下,采用CCS同时极化波比正负斜率LFM有更好的旁瓣抑制和波形正交性,成像结果也表明所提仿真方法的有效性得到了验证。本文还进一步就极化通道非理想特性对目标散射矩阵Pauli分解的影响进行了EM仿真,为后续同时极化波形性能验证、目标特征提取及识别研究奠定了基础。需要强调的是,本文方法同时适用于其他体制雷达回波信号的EM仿真。