一种基于TRT-SKT-HAF的变加速目标快速相参积累算法

陈 锴,乔 良,李 明*,陈洪猛

(1. 西安电子科技大学 雷达信号处理国家重点实验室, 陕西 西安 710071) (2. 北京无线电测量研究所, 北京 100854)

0 引 言

随着现代科学技术的不断发展,越来越多的高速机动目标出现在战场中,这类目标具有高速、强机动和弱回波能量等特征,对传统雷达的检测性能提出了严峻的挑战,为此高速机动目标的检测以及高精度运动参数估计的研究受到了学术界的广泛关注[1-3]。长时间相参积累可以有效提高此类目标的检测概率,然而由于目标的机动性,目标在积累时间内会产生距离走动(RM)和多普勒徙动(DFM)现象,严重影响相参积累的性能[4-6]。

在目前的匀速目标检测算法中,文献[7]提出利用一阶keystone变换(KT)来解决目标在长时间内的RM现象,该方法无需掌握目标的运动参数信息,仅通过尺度变换就可实现RM校正,但KT在校正高速目标的RM时,需要对速度模糊数进行搜索,加大了运算复杂度。文献[8]提出Radon傅里叶变换(RFT)方法对目标运动参数进行搜索以实现相参积累,然而由于离散脉冲采样、有限的距离分辨率以及积累时间受限等原因,RFT的积累结果容易产生峰值较高的盲速旁瓣(BSSL),导致严重虚警。以上两个方法在忽略目标机动性,仅考虑目标速度的情况下均能实现线性RM校正和目标能量积累,但无法解决目标加速度引起的DFM。

针对匀加速目标产生的DFM,许多学者在KT和RFT变换的基础上提出了很多有效的算法,如文献[9]利用线性距离徙动矫正去除线性RM和多普勒中心频率,然后采用二阶keystone变换(SKT)来补偿距离弯曲。文献[10]通过一阶KT校正目标速度引起的RM,随后进行多普勒中心频率估计与补偿,最后利用SKT校正加速度引起的距离弯曲,但文献[9]和文献[10]均未考虑多普勒模糊问题,不适用于高速目标。文献[11]研究了多普勒模糊下的高速机动目标相参积累问题,提出了基于SKT-RFT的相参积累算法,该算法利用SKT校正距离弯曲后,通过分数阶傅里叶变换补偿DFM,最后利用RFT实现相参积累。然而SKT-RFT对RM的校正以及多普勒走动的补偿是分步进行的,因此低信噪比(SNR)条件下算法的积累性能会严重下降。文献[12]提出了基于Radon分数阶傅里叶变换(RFRFT)的相参积累算法,该算法可实现低SNR下的微弱目标检测,但需要在距离-速度-加速度域上进行三维搜索,提高了计算复杂度。

针对变加速运动目标,不仅存在DFM,还会产生多普勒弯曲。为此,文献[13]提出了具有任意参数化机动目标的广义RFT变换(GRFT)。但是,GRFT需要多维搜索目标的运动参数,运算复杂度很大,并且会出现BSSL导致虚警。文献[14]提出一种基于Radon分数阶模糊函数(RFRAF)的变加速目标相参积累算法,该算法对速度-加速度-加加速度在三维空间上进行参数搜索,与GRFT相比,计算复杂度更高。文献[15]提出一种将广义KT和广义去调频技术结合的相参积累算法,但该算法多次使用KT,带来较大的能量损失,并且仍需对多普勒模糊数、加速度和加加速度进行参数搜索。除此之外,广义傅里叶变换[16]、Radon线性正则变换[17]等也是目前较为流行的典型算法,但以上几种算法都无法避免参数搜索,随着信号采样点数和积累时间的增加,算法运算量陡升,影响目标的实时检测性能。为降低运算复杂度,文献[18]和文献[19]提出了一些典型的基于相邻相关函数(ACCF)的快速相干积分算法,如迭代ACCF[18]和相邻相关函数-吕分布算法(ACCF-LVD)[19]。基于ACCF的算法能够以较低计算复杂度实现RM和DFM的校正,但需要目标在相邻时间之间的RM处于同一个距离单元内。

本文在以上研究的基础上,针对上述算法在处理高速机动目标回波信号时计算量过大、受多普勒模糊影响以及低信噪比积累性能不佳等问题,提出了一种基于慢时间序列反转变换(TRT)-SKT-高阶模糊函数(HAF)的变加速目标快速相参积累算法。该算法首先利用TRT对目标速度和加加速度造成的一阶和三阶RM以及DFM进行统一校正,再通过SKT消除加速度引起的二阶RM。接着提取目标所在距离单元信号,运用HAF法从该线性调频信号估计出目标的加速度,用所得加速度构建相位补偿函数以校正剩余的DFM,最后对回波信号在多普勒域进行快速傅里叶变换(FFT)实现相参积累。本文所提算法无需对目标运动参数进行搜索,不受多普勒欠采样的影响,极大地降低了算法运算复杂度,并且在低SNR情况下,仍然有着较好的检测性能。

1 回波信号模型

假设雷达发射线性调频(LFM)信号

(1)

式中：rect(·)表示矩形窗函数;Tp为脉冲信号宽度;u为发射信号的调频率;t为单个脉冲时间内的快时间变量;fc为载频。

雷达发射的脉冲数为M,脉冲重复时间间隔为Tr,则在整个脉冲持续时间内,慢时间变量可以表示为tm=mTr(m=0,1,…,M-1)。针对变加速目标,假设只考虑径向运动参数,其初始距离、径向速度、径向加速度和径向加加速度分别表示为R0、c1、c2和c3,目标相对于雷达在tm时刻的瞬时距离可以表示为

(2)

忽略噪声,雷达接收的基带回波信号可以表示为

(3)

式中：A为回波信号幅度;c为光速;λ=c/fc为信号波长。对基带回波信号进行脉冲压缩,得到脉压后的回波信号

(4)

式中：A0为回波信号经过脉压后的信号幅度;B为信号带宽;sinc(x)=sin(πx)/πx表示为sinc函数。由式(4)sinc(·)项可知,脉压回波的包络位置随着慢时间的变化而改变。

2 算法原理

本文算法原理框图如图1所示。该算法首先在距离频率-方位时域上利用TRT对目标速度和加加速度造成的RM以及DFM进行统一校正;然后采用SKT消除加速度引起的距离弯曲。此时目标的RM得到完全校正,提取目标所在距离单元的慢时间序列,该序列为一个LFM信号,运用HAF法从该LFM信号估计出目标的加速度,用所得加速度构建相位补偿函数以校正加速度带来的DFM。最后对回波信号分别在时域进行逆快速傅里叶变换(IFFT),在多普勒域进行FFT实现相参积累。

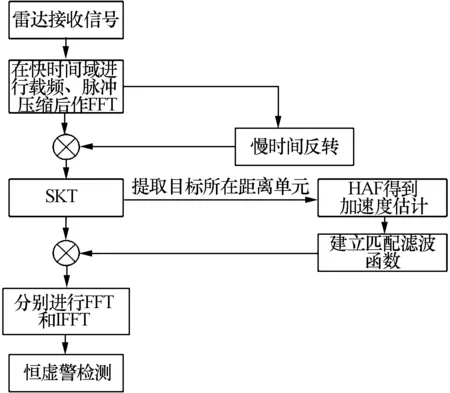
图1 算法原理框图

下面分别从单目标和多目标情况对基于TRT-SKT-HAF的变加速目标快速相参积累算法原理进行详细阐述。

2.1 单目标

对式(4)沿快时间维度进行FFT,得到距离频率域的回波信号

(5)

当目标速度比较快而雷达的脉冲重复频率比较低时,会发生欠采样现象,此时目标速度可以表示为

c1=va+nvamb

(6)

式中：va=mod(c1,vamb);n为模糊数;vamb为盲速。将式(6)代入式(5)得

(7)

式(7)存在四个相位项,后面三个相位项均存在慢时间变量和距离频率的耦合,下面介绍TRT-SKT-HAF算法分别对耦合相位项进行处理。

将式(7)沿慢时间反转然后与原式相乘得到

T(tm,f)=S(tm,f)·S(-tm,f)=

(8)

由式(8)知经过TRT变换后,目标速度及加加速度带来的RM得到校正,但慢时间变量和距离频率的耦合仍存在。对式(8)作SKT处理,令

(9)

代入式(8)得

(10)

对式(10)沿距离频率维作逆傅里叶变换得

(11)

由式(11)可知,当完成SKT后,目标回波的RM已完全校正,信号快时间维峰值均在4R0/c对应的距离单元内,取峰值所在距离单元的慢时间信号得

(12)

此时信号是一个关于慢时间变量tn的复单频信号,其二阶瞬时矩可以表示为

s2(tn;τ)=s(tn)·s*(tn-τ)=

(13)

式中：τ为常数时延。式(13)的二阶模糊函数为

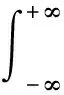
(14)

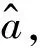
(15)

将式(15)与式(10)相乘后沿快时间维作IFFT得

(16)

由式(16)可知,当目标加速度估计等于真实加速度时,加速度所在相位项可以被完全补偿。此时对信号沿慢时间作FFT得到

(17)

由式(17)可知,目标能量被积聚在同一个距离单元和多普勒单元中,且多普勒单元始终位于频率为0处。

2.2 多目标

考虑多目标脉压后的距离频率域回波信号

(18)

式中：A1,i为脉压回波经过FFT后目标i的振幅。将式(18)沿慢时间轴反转后与原式相乘得

(19)

式(19)第一项是信号自项,可以用来进行相参积累,并且信号自项处理过程中的FFT和IFFT都是线性过程,最后自项和的输出也是各个目标积累结果的叠加。第二项为不同目标之间的交叉项,Scross(f,tm)的具体表达式为

(20)

接下来同样进行SKT处理,代入式(9),得到

(21)

其中Scross(f,tn)为

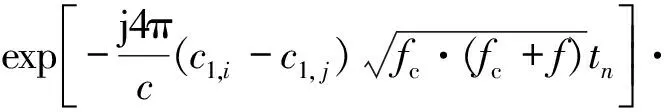
(22)

观察式(21)和式(22)可知,信号自项的RM已经校正,但是交叉项仍存在RM现象。此时对回波信号进行脉冲积累,信号自项会聚焦,而交叉项由于存在RM,其能量无法得到聚焦。接下来分别提取出各个目标单元所在的慢时间序列,利用HAF得到各目标的加速度估计。假设现得到目标i的加速度估计,建立匹配滤波函数如下

(23)

将匹配滤波函数与式(21)相乘,此时目标i的DFM得到消除,对回波信号在慢时间维作FFT,目标i就能实现相参积累。

2.3 算法实现

根据图1给出的算法原理框图,本文所提算法的具体实现步骤如下：

(1)对雷达接收的LFM回波信号在快时间域进行去载频和脉冲压缩处理后做FFT,得到在距离频域-慢时间域上的回波信号为S(tm,f);

(2)S(tm,f)沿慢时间维度进行反转得到S(-tm,f),将其与原式相乘得到T(tm,f),通过TRT处理可以校正目标因速度带来的一阶RM、加加速度带来的三阶RM和DFM;

(3)对T(tm,f)用线性插值的方法在慢时间轴作SKT处理得到T(tn,f),此时目标RM已经完全校正;

(4)提取目标所在距离单元的慢时间序列,利用HAF估计出目标加速度后建立匹配滤波函数与T(tn,f)相乘消除加速度带来的DFM;

(5)对经过匹配滤波后的T(tn,f)分别沿距离频率f进行IFFT和慢时间tn进行FFT,实现目标能量的相参积累;

(6)提取步骤(5)中积累幅度最大值,通过设计的恒虚警检测器来判断有无目标。

3 仿真实验分析

3.1 单目标仿真

假设一个机动目标,与雷达之间的初始距离为200 m,初始速度为400 m/s,初始加速度为20 m/s2,初始加加速度为25 m/s3,雷达系统参数如表1所示,脉压后的信噪比为-5 dB,仿真结果如图2所示。对回波信号进行距离向脉冲压缩后得到脉压结果如图2a)所示,观察结果图发现目标轨迹有明显的高阶RM。图2b)为直接对回波信号进行动目标检测(MTD)的积累结果,可以看到目标能量分散在距离单元和多普勒单元上,无法得到积累。图2c)是经过TRT的结果,经过TRT处理后加加速度带来的高阶RM和速度带来的线性RM都得到了有效的校正,剩下加速度带来的二阶RM未校正。图2d)是经过SKT处理后的结果,可以发现目标RM已得到完全校正,目标被拉回到同一距离单元内。随后提取目标所在距离单元,对其进行HAF处理得到加速度估计如图2e)所示。最后对回波信号进行加速度匹配滤波后在多普勒域做FFT得到相参积累结果如图2f)所示。从图2a)～图2f)的仿真结果可知,本文所提方法有效地对单个变加速目标实现了长时间相参积累。

表1 雷达系统仿真参数

图2 单个目标仿真结果

为比较所提算法在低信噪比下与其他算法的积累性能,图2g)～图2j)分别给出了TRT-SKT-HAF、GRFT、迭代ACCF以及RFRAF算法在脉压后SNR为-10 dB下的仿真结果。由图2g)可知,TRT-SKT-HAF算法在低信噪比下仍很好地实现了目标能量的积累。图2h)是GRFT算法的积累结果,虽然GRFT也能实现目标回波信号的相参积累,但在高峰值附近出现了很多BSSL,容易造成虚警。图2i)是迭代ACCF算法的积累结果,观察发现目标峰值发生了分散,该算法在低SNR下的积累效果欠佳。图2j)是RFRAF算法的积累结果,RFRAF虽实现了目标能量的积累,但存在一些BSSL现象。由图2g)～图2j)可知,本文所提算法在低SNR下对单个变加速目标的积累性能优于其他算法。

3.2 多目标仿真

假设两个运动目标,雷达系统参数如表1所示,设定脉压后的信噪比为-5 dB,目标运动参数如表2所示,多个目标仿真结果如图3所示。

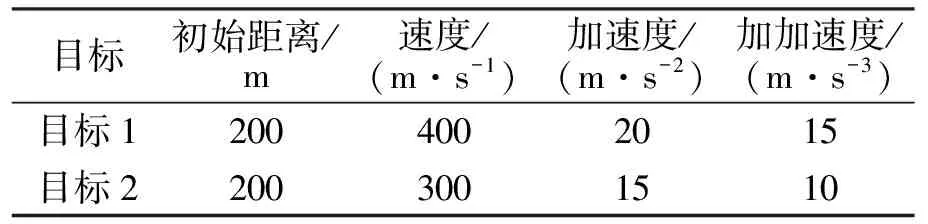
表2 多目标运动参数

图3 多个目标仿真结果

对回波信号进行距离向脉冲压缩后得到脉压结果如图3a)所示,观察结果图发现两个目标轨迹都出现了高阶RM。图3b)为直接对回波进行MTD的积累结果,可以看到目标能量分散在距离单元和多普勒单元上,能量无法得到积累并且无法区分两个目标。图3c)是经过TRT处理的结果,两个目标经过TRT处理后RM得到了一定的校正,剩下各自加速度带来的二阶RM未校正。图3d)是经过SKT处理后的结果,可以发现两个目标RM已得到完全校正。随后提取各自目标所在距离单元,对其进行HAF处理得到各自加速度估计如图3e)、图3f)所示。最后对回波信号分别进行加速度匹配滤波后得到相参积累结果如图3g)、图3h)所示,目标1、2都得到了有效的积累,且不受交叉项的影响。从图3a)～图3h)的仿真结果可知,本文所提方法有效地对多个变加速目标实现了长时间相参积累,并得到了各目标的加速度信息。

图3i)～图3l)是多目标情况下其他算法的积累结果。图3i)是GRFT的积累结果,观察可知GRFT算法在多目标情况下仍存在着严重的BSSL现象。图3j)是迭代ACCF算法的积累结果,由图可知,个别目标峰值幅度较低,积累效果不佳。图3k)和图3l)是RFRAF的积累结果,和单目标情况相似,同样存在一些BSSL。结合图3g)～图3l)可知,本文算法在多目标情况下的积累性能同样优于其他算法。

3.3 运算复杂度分析

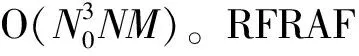
表3 不同算法运算复杂度比较

图4 不同算法运算复杂度比较图

假设M=N=N0,那么TRT-SKT-HAF、GRFT、RFRAF和迭代ACCF四种算法的运算复杂度分别如下：O(M2log2M)、O(M5)、O(M6log2M)和O(M2log2M),可知本文所提算法的运算复杂度相比GRFT减小了3个数量级,相比RFRAF减小了4个数量级,与迭代ACCF算法复杂度相当。

3.4 检测性能仿真

假设实验的恒虚警率设置为10-4,雷达系统仿真参数如表1所示,目标的运动参数与3.1节单目标仿真运动参数设置一致。输入SNR区间为[-25,20] dB,分别对每一种算法在其SNR区间上进行500次蒙特卡洛实验,得到的仿真结果如图5所示。由图5可知,本文所提算法的检测性优于PHAF算法、RFT算法、RFRFT算法和RFRAF算法,这是因为本文算法有效地校正了目标的高阶RM和DFM。本文所提算法虽然在检测SNR门限上比GRFT算法高3 dB,但有更低的运算复杂度且不需要对目标运动参数进行搜索,仿真结果表明所提算法达到了算法复杂度和检测性能的平衡。

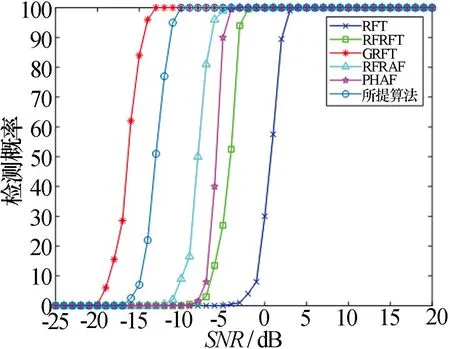
图5 不同算法的检测性能度比较结果图

4 结束语

高速机动目标的回波信号在相参积累时间内会发生严重的RM和DFM现象,制约着雷达对运动目标的检测性能。针对传统算法在处理这类目标回波信号时计算量过大、受多普勒模糊影响以及低SNR积累性能不佳等问题,本文提出了一种基于TRT-SKT-HAF的变加速目标快速相参积累算法,该算法具有以下优点：(1)无需考虑多普勒模糊带来的影响;(2)无需对目标速度、加速度以及加加速度进行任何参数搜索操作,同时可以有效校正RM和DFM,计算复杂度较低,便于工程实现;(3)能够获取目标的加速度信息,并利用加速度估计实现相参积累;(4)对多目标产生的交叉项能够有效抑制,可实现多个目标的相参积累。