微波光子信号同步及其在分布式相参雷达中的应用

潘时龙,章志健,王祥传*,刘 熙,杨思豪,曹欣荣,王立晗,程 强,3,4,马 丛,丁泽勇,郭德明,伍光新

(1. 南京航空航天大学 微波光子技术国家级重点实验室, 江苏 南京 211106) (2. 南京电子技术研究所, 江苏 南京 210039; 3. 雷达探测感知全国重点实验室, 江苏 南京 210039) (4. 江苏省探测感知技术重点实验室, 江苏 南京 210039)

0 引 言

战场环境探测与感知是现代战争中敌我双方博弈的焦点领域,对雷达等关键军事电子装备的性能提出了极高的要求。受到体积、重量和功耗等因素的限制,单平台雷达的探测性能越来越难以提升。此外,由于单平台雷达在空间维度上的单一性,它极易被定位和干扰,导致其在战场上的生存能力受到严重威胁[1]。与此相对,分布式孔径雷达通过布设多个独立、分置的雷达单元,利用空间分集的方式对目标进行探测,实现了高性能雷达“化整为零”的结构改变。这种方式不仅显著降低了雷达对平台资源的需求,还为雷达提供了新的空间维度,从而提高了其可靠性、灵活性和抗干扰能力[2]。根据信号处理方式的不同,分布式孔径雷达按工作体制可分为非相参体制和相参体制[3]。分布式非相参雷达采用数据级融合处理方式,可以实现信息的协同,但丢弃了信号相位等信息,对于提高雷达射频相关性能的增益有限。而分布式相参雷达采用信号级融合处理方式,通过相参叠加,可有效提高系统的信噪比。例如,将N部雷达单元进行收发相参,理论上可将信噪比提升N3倍,从而显著提升系统的探测威力与跟踪能力。此外,分布式相参雷达还能将空间分置的天线合成庞大的虚拟孔径,大幅提升系统的角分辨能力。

基于上述独特优势,自2003年美国林肯实验室提出分布式相参雷达概念以来,分布式相参技术已成为现代雷达前沿领域的研究热点。2004年和2005年,林肯实验室分别进行了两次全相参外场实验,利用两个分布式雷达单元成功对水塔、飞机和火箭等复杂目标开展了探测,实现了接收相参近6dB、全相参近9 dB的合成增益[4]。随后,该实验室又分别在2008年和2014年验证了Ku波段和W波段分布式相参雷达的可行性和相参性能[5-6]。在国内,针对分布式相参雷达中的节点布阵方式、信号同步技术、相参处理方法、系统研制和性能评估等关键内容,北京理工大学[7]、南京航空航天大学[8-9]、清华大学[10]、南京电子技术研究所[11]、北京无线电测量研究所[12]等多家单位开展了广泛研究,取得了一系列重要成果,成功验证了分布式相参雷达的可行性和性能优势。

然而,目前国内较为成熟的分布式相参雷达工程验证大多集中在低频段的地基雷达系统中,主要原因在于实现分布式相参雷达的物理基础是平台间信号的时间(时)、空间(空)、频率(频)、相位(相)同步,而随着工作频段和带宽的增加,分布式相参雷达对信号时、空、频、相的同步精度要求越来越高,使得传统电学同步技术面临着诸多难题。如：在有线同步方式中,电缆较大的传输损耗[13]限制了分布式相参雷达的布设范围及灵活性,同时电缆的有限传输带宽也制约了同步精度的进一步提升;而基于射频无线的同步方式,则面临射频波束较宽和多径干扰等问题[14-16],难以满足高频分布式相参雷达对高同步精度的需求。

相较于传统电学技术,微波光子技术因其高频、宽带、低损耗和可并行处理等特点[17],在微波信号产生、传输、处理和测量等方面表现出了独特的优势,为分布式相参雷达的高精度时、空、频、相同步需求提供了新的解决手段[18-20]。本文首先介绍了分布式相参雷达对信号时、空、频、相同步的要求,然后阐述近年来面向分布式相参雷达的微波光子时、空、频、相同步技术的研究进展,最后构建了原理验证系统,验证了微波光子分布式相参雷达的可行性,以期为分布式相参雷达的发展提供新的思路。

1 分布式相参雷达对信号同步性能的要求

图1为微波光子分布式相参雷达的典型架构,包括中心节点和远端节点。各节点之间通过光链路(光纤或者空间激光)连接,形成了一个微波光子时、空、频、相同步和信号传输网络,实现各个节点间的信号同步,为分布式相参探测提供物理基础。

图1 微波光子分布式相参雷达典型架构

为了达到接近理论极限的信噪比增益,必须保证各雷达单元在时、空、频、相同步等方面严格满足相参约束条件。式(1)为相参增益损失与时、频、相同步误差的关系[21]

(1)

式中：N为节点个数;B为信号带宽;ΔTi与Δφi分别是时间和相位同步误差。由式(1)可以看出,相参增益损失随时、频、相同步误差的增加而增大。若要使相参增益损失不超过0.3 dB,其相位同步误差应小于15°,时间同步误差应小于0.16/B[22]。因此,为满足高频、宽带分布式相参雷达的需求,亟需突破更高精度的时、频、相同步技术。

在空间同步方面,为了获得高角度分辨能力、抗干扰能力和抗毁伤能力,分布式孔径雷达通常希望长的基线[23],这要求各雷达平台间的空间基线测量具有大的测量范围。此外,雷达天线的位置抖动以及雷达平台间的相对运动将直接耦合到信号相干叠加时的相位抖动和变化中,导致相参增益降低。以X波段雷达为例,15°的相位同步精度需要毫米级精度的三维空间位置测量。因此,分布式相参要求空间同步技术兼具高精度和大范围特性。需要注意的是,考虑到目标回波的相关性,分布式协同相参雷达对节点间基线长度有着以下典型约束[24-25]

(2)

式中：Φmax为最大约束相位偏差;λ为信号波长;R为目标到基线中心点的距离;L为目标垂直于视线方向的长度;θ为目标中心到基线中心连线与地面的夹角。因此,对空间同步范围的要求需根据分布式相参的实际应用场景确定。

2 微波光子信号同步技术

2.1 微波光子相频同步技术

在分布式相参雷达系统中,各雷达节点时钟(本振信号)的相位和频率稳定性至关重要。任何微小的抖动都可能引发探测信号及回波信号的相位误差,从而直接影响到相参合成增益。因此,实现高精度的信号相频同步是实现高性能分布式相参雷达的关键。

目前,基于微波光子学的信号相频同步技术主要分为主动相位补偿法和被动相位失真法两类。主动相位补偿法通过检测在链路中往返传输前后的微波信号的相位差,并利用反馈控制器件实现对该相位差的补偿。当前,常见的主动相位补偿技术包括使用可调延时线和压控振荡器等进行反馈预补偿[26-28]。图2为基于可调光延时线主动补偿方法的典型架构。在此方案中,中心节点的本振信号被调制到一个光载波上,经过可调光延时线使信号相位增加预补偿值φ0后在光纤链路进行往返传输,鉴相器以中心节点参考源信号相位为基准,检测回传信号的相位变化,包括预补偿值φ0和链路传输过程中的相位抖动值φ1。利用鉴相器输出结果反馈控制可调光延时线对链路延时抖动进行预补偿后送入单模光纤进行传输,从而使远端节点接收信号的相位保持稳定。

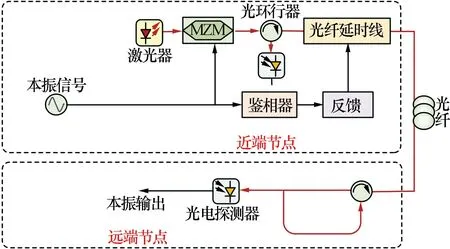
图2 基于可调光延时线主动补偿的稳相架构

虽然主动相位补偿法能够提供较高的相位同步精度,但受限于补偿器件范围有限、速度慢等问题,难以适应动平台场景下相频参数变化剧烈的情况。

被动相位失真技术通过相位共轭实现相位抖动的预补偿,进而实现相位同步,具有结构简单、补偿速度快、补偿范围不受限等优点。该技术通过将参考信号和携带有链路抖动信息的探测信号进行混频,得到相位共轭信号后再次传输,从而实现信号相位抖动的被动消除。这种技术不需要使用复杂的主动补偿器件、鉴相模块和控制模块等,更适用于灵活组网分布式相参雷达系统。

图3为基于被动相位失真的光载射频稳相技术的典型架构。首先,在中心节点处产生一个本振信号V1

V1=cos(ωt+φ0)

(3)

图3 基于被动相位失真的稳相传输架构

式中：ω是信号的角频率;φ0是初始相位。该本振信号被分成两路,一路经过分频器获得频率为ω/2的辅助信号Va

(4)

该辅助信号Va再次被分为两路,一路通过电光调制器调制到光载波上,经过光链路传输到远端。在远端节点,接收到的光信号由光电探测器探测后调制到另一个光载波上以进行波长转换。随后,调制光信号通过同一光链路反向传输回中心节点。在中心节点,利用光电探测器将回传的光信号转换成电信号Va,r

(5)

此时,该电信号中携带了链路往返传输时引入的链路延时及其抖动信息τ。

在中心节点,本振信号的另一路与辅助信号的另一路混频后获得信号V2

(6)

信号V2与Va,r混频后得到预失真信号V3

V3=cos(ω(t+τ)+φ0)

(7)

将预失真信号调制到光载波上并传输到远端节点,消除掉链路抖动,在远端节点即可获得与中心节点本振信号相位完全一致的信号V4

V4=V1=cos(ωt+φ0)

(8)

南京航空航天大学基于上述架构[29],在20 km的光纤中成功传输6 GHz射频信号,实现了小于1.17 ps的相位抖动。相比之下,未使用该方法时的相位抖动大于41 ps。西南交通大学提出了一种基于双驱动MZM的光链路被动稳相传输方案[30],利用该方案在50 km单模光纤上实现了10 GHz射频信号的稳定传输,10 h内相位抖动均方根(RMS)为0.82 ps。随后,该团队又提出了一种单激光器被动相位稳定射频传输方案[31],由于抑制了非相干瑞利散射噪声,该方案显著提高了系统稳定性;在50km单模光纤上传输5 GHz射频信号时,与没有处理非相干瑞利散射噪声的情况相比,新方案在10 kHz偏移处的单边带调制相位噪声降低了10.9 dB。同时,在1×104s内,相位抖动均方根仅为1.12 ps。

当分布式雷达节点数量增多时,上述点对点的稳相技术难以进一步满足需求。为此,南京航空航天大学提出了一种基于偏分复用的多节点本振信号稳相传输方法[32]。如图4所示,在中心节点,原始信号被分为两路,其中一路信号经过二分频后由双偏振马赫-曾德尔调制器调制到光载波的X偏振态上,并将其作为探测信号往返传输。返回中心节点的探测信号经过滤波后和原始信号进行混频生成预失真信号。随后将预失真信号调制到Y偏振态上分发给远端节点。在远端节点,将前向和后向传输光信号分离。前向传输的预失真信号调制到Y偏振态上,后向传输的探测信号调制到X偏振态上。光载波通过检偏器后经光电探测器恢复得到两个频率相同(原信号二分之一)、相位抖动互补的信号,这两个信号混频后理论上将完全消除相位抖动,从而得到相位稳定的信号。利用该方案将5 GHz射频信号传输到10 km和15 km两个节点处时,RMS定时抖动分别为1.09 ps(约0.03 rad)和1.59 ps(约0.05 rad)。

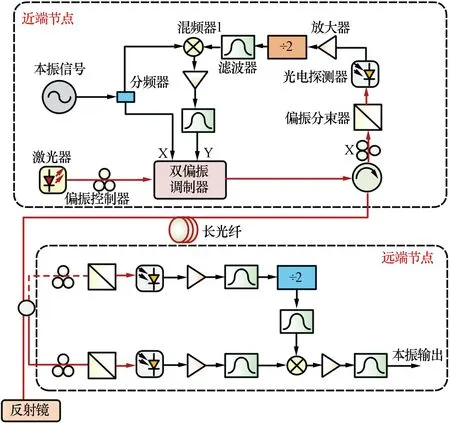
图4 基于偏振复用的多节点被动稳相传输架构

综上所述,微波光子被动相位失真技术得益于简单的系统结构、高响应速度和不受限制的补偿范围等优势,有望为分布式相参雷达提供高精度的相频同步手段。

2.2 微波光子时间同步技术

信号级相参合成要求不同雷达单元收发的信号在时间上实现精准对齐,这就需要各雷达单元必须基于统一的时间基准进行操作。目前,在分布式相参雷达中,根据信号传输手段可将常用的时间同步技术大致分为两类：基于无线射频链路和基于激光链路。在无线射频链路的时间同步方案中,通过微波双向比对技术,可以在大范围内实现节点间的时间同步。这种方案具有灵活可重构组网的优势,但其同步精度易受波束宽度和多径效应影响;作为此类技术的代表,卫星授时系统能够为分布式网络提供广域覆盖的时间同步服务。但受限于环境(温度、电离层变化、多径等)的扰动,其同步精度只能达到ns量级[14-16]。相比之下,基于激光链路的时间同步技术具有窄波束、大带宽、低损耗等优势,能够实现更高时间同步精度,是满足宽带分布式相参雷达时间同步需求的有效技术途径。具体方法包括单向时间环回法与双向时间对比法。

单向时间环回法直接通过光链路将时间信号分发至远端节点。该方法通过实时测量时间信号从中心节点到远端节点的传播时延[33],在中心节点进行时延补偿,使时间信号稳定地分发至远端节点。图5为单向环回时间同步系统的典型架构。首先由中心节点时钟生成两个1PPS信号,一个信号被送入近端的时间间隔计数器,而另一个则用于调制波长为λ1的光信号,随后该信号经由波分复用器传送至远端节点。在远端节点,时间信号由解调器提取出来作为时间基准,并再次被调制到波长为λ2的光信号上,回传到中心节点。中心节点的时间间隔计数器测量往返时延后,对传输时延进行精确补偿,保障远端节点时间基准的稳定性。

图5 基于单向环回法的时间同步系统架构

基于单向时间环回法,波兰克拉科夫AGH科技大学采用两个互补AMS-0.35 μm CMOS工艺制造的电延时线,对链路时延漂移进行了实时补偿,在60 km的光纤链路中实现了12 ps的峰峰时间同步残余波动[34]。清华大学和中国计量科学研究院将时间信号与9.1 GHz微波信号调制到不同波长上,并通过波分复用技术经由同一光纤传输。他们在中心站补偿传输引起的噪声,最终实现了80 km传输距离下50 ps的时间同步精度[35]。上海光机所进一步将时间和频率信号调制到同一个光载波上,其中时间信号通过相位调制,而频率信号通过强度调制,并在中心节点控制光学延迟线主动补偿链路中的时延漂移噪声,在110 km的光纤链路上实现了小于120 ps的峰峰值时间漂移[36]。南京航空航天大学基于微波光子相推法在公里量级的大气信道链路上实现了精度优于0.1 ps的时延测量和实时补偿。该链路无需额外的硬件,所用器件带宽仅为10 MHz。研究团队结合动态卡尔曼滤波有效地抑制了由大气湍流引起的测量误差。在闭环控制时,系统时间抖动为0.11 ps,时间抖动的标准偏差为0.28 ps[37]。尽管单向环回法具有结构简单的优势,其远端时间信号的稳定性高度依赖链路的稳定性,且同步性能受补偿器件的范围和精度限制。

双向时间对比法的原理如图6所示。在该技术中,两地都有参考时钟,其同步性能受链路时延波动影响较小,拓展性较强。以1PPS时间信号为例,设定全域时间基准下中心节点A时钟发出时间信号的时刻为t1,远端节点B时钟发出时间信号的时刻为t2,则两端的钟差ΔT=t2-t1,代表着B端时钟滞后于A端时钟的值。

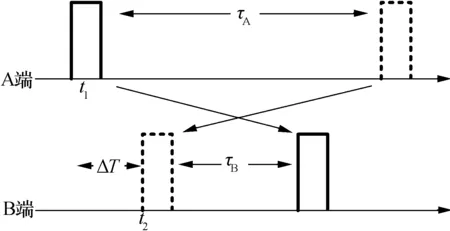
图6 基于双向时间对比时间同步原理图

为方便表达,假设两端采用同样的设备,此时可认为两端信号发生器的发送时延和时延解算模块的接收时延是同一固定值,并可通过初始不对称性标定校准。令时间脉冲信号从A端发射到B端所需要的时间为τA,从B端发射到A端所需要的时间为τB,则在该基准下发射端和接收端同时进行绝对时延测量的结果分别为

(9)

式中：τAB、τBA为传输路径时延。由于初始钟差固定,且双向传输链路具有对称性,可认为τAB=τBA,则两端钟差可表示为

ΔT=(τA-τB)/2

(10)

将A端测量到的时间间隔值τB传至B端,在B端计算便可得到钟差。随后,在B端对该钟差进行补偿即可实现两端的时间同步。

图7为典型的微波光子双向对比时间同步系统架构。首先,A、B端时间信号经过时延调节后由光发送模块发送至另一端。两端采用不同的光波长,以减少后向散射与端面反射的影响。随后,时间信号经光电转换后,与本地时间信号送入时间间隔计数器,解算出两端接收时延差。最后,将A端时延差信息传输到B端,在B端解算出两端钟差后,通过调节时延模块补偿钟差,实现两端时间同步。

图7 基于双向对比法的微波光子时间同步系统结构

基于双向时间对比法,上海交通大学吴龟灵团队结合时分复用技术在实验室13 134 km等效长度的光纤链路上实现了稳定度优于30 ps的时间同步[38]。随后,该团队又基于波分复用时频同传技术,在62 km的光纤链路上实现了时频同时传输,时间同步精度达到3.5 ps/s[39]。中国科学院国家授时中心利用超窄激光器产生传输信号,并引入色散误差修正机制,在1 085 km的光纤链路中实现了18 ps的时间同步标准差[40]。

在双向对比时间同步技术的研究中,光频梳凭借其在频域和时域都具有极高的稳定性,可作为高稳定的时间基准受到广泛关注。美国国家标准与技术研究院的Jean-Daniel等[41]在2015年首次结合线性光学采样技术,实现了基于光频梳的时间同步,其系统架构如图8所示。该系统利用不同重频光频梳之间脉冲的周期性干涉实现飞秒级时延差测量进而提高时间同步精度：首先分别测量出近、远端节点本地频梳与传输频梳的钟差,然后实现基于双向时间对比的钟差解算,最终在远端节点通过10 Hz带宽的比例积分控制器反馈控制调节时延,使得两端时间同步。两天内4 km空间链路的时间漂移仅40 fs;而在6 500 s时间内,该漂移甚至低于1 fs。四年后,该团队结合色散补偿技术与多普勒抑制算法,使用装载24 m/s高速扫描延时线反射光路的四轴飞行器,在4 km空间链路内实现了1 fs的时间同步标准差[42]。中国科学技术大学也采用光频梳线性采样方案,在16 km自由空间链路中实现了优于10 fs的时间比对精度[43],随后利用两对线性采样系统在113 km空间链路中实现了优于0.5 fs/30 s的时间比对精度[44]。基于光频梳的时间同步因具有极高的精度,非常适合基于空间激光链路的同步场景。但当这项技术被应用于光纤链路时,其性能会受色散等因素影响,优势难以发挥。

图8 基于线性光学采样的时间同步系统架构

2.3 微波光子空间同步技术

在分布式相参雷达系统中,天线空间位置的变化将直接耦合到相位同步误差中,降低雷达的相参增益。因此,精准地获取各单元雷达天线的空间位置是实现高相参增益的前提。目前能实现高精度三维空间位置测量的技术主要包括激光测距技术、全球导航卫星(GNSS)[45]技术等。

由于激光光束定向性强、波长短等优势,激光测距技术的典型测量精度可达±0.3 μm/m。为实现高精度空间位置测量,目标角度信息的精准测量同等重要。但目前激光测距类仪器的测角精度(典型值±0.5″)较低,测距精度与测角精度还难以匹配,极大限制了对目标的定位性能。为解决这一问题,可以使用激光多边法对物体的位姿状态进行测量。激光多边法同时使用多台激光跟踪干涉仪组网测量目标物体的姿态,如图9所示。利用四个已知坐标的测量基站(A,B,C,D),只要测出PA,PB,PC,PD四个长度就能够求解待测天线P的三维位置坐标。天津大学基于独立式双轴驱动方法研制了一种4路的激光跟踪三维坐标测量系统[46],实现了平均值约2.4 μm的三维坐标测量误差;中国计量科学院基于激光多边法研制出一种坐标测量误差优于8.9 μm的测量系统[47]。激光多边法测量精度主要受限于其测量基站的数量。而当测量基站数量增加时,系统参数标定和计算复杂度也随之增加,导致系统结构复杂、成本高昂。此外,在强光照射或大气污染等恶劣天气影响下,激光测距的测量精度和稳定性会严重下降。

图9 基于激光测距的空间位置测量原理

基于GNSS的空间位置测量技术,是通过导航卫星将它们的轨道信息编码到信号中并广播,地面接收站捕获这些信号后,通过解算获得卫星的精确位置以及地面目标与卫星之间的准确距离,从而得到目标在三维空间中的位置信息。该技术以其高精度、良好的稳定性和无累积误差等特点,成为了一种可靠且有效的空间位置测量方法。

为提高测量精度,GNSS空间测量系统通常采用差分技术来消除卫星轨道误差、电离层和对流层延迟等对载波相位的影响。目前,差分技术主要分为载波相位双差模型和单差模型。双差模型通过对单差模型进行二次差分,进一步消除了不同天线接收机之间的传输时延。然而,受限于卫星的几何分布不均匀,双差模型对于垂直方向上的位移变化量不够敏感,其垂直方向的测量误差是水平方向的三到五倍。通常情况下,基于双差模型的GNSS空间测量技术在测量精度上仅能达到厘米量级。为拓展测量范围,GNSS空间测量系统将各天线接收到的导航信号通过电缆或光链路传输至接收机进行载波相位提取。电缆由于传输损耗大,会大大限制系统的测量范围。相比之下,通过低损耗的光链路可以实现更大范围的空间基线测量。此外,由于光链路可以实现大范围传输时延的实时监测,采用单差算法即可结算三维坐标,并有效解决传统双差技术在垂直方向精度不足的问题。

在载波相位单差模型中,原始载波相位观测方程为

(11)

通过对不同天线处的载波相位观测量进行差分运算,可以得到载波相位单差模型

(12)

(13)

图10 基于GNSS的空间位置测量原理

接收机钟差可通过在接收机做共时钟处理而消除,由此可得到单差后的载波相位为

(14)

令观测到的卫星数量为N,我们得到单差模型的矩阵表达式为

λΔφij-LBi=SkbT+λΔNij

(15)

图11 基于线性调频光时延测量的GNSS空间同步系统

综上所述,基于激光测距的同步方案测距精度高,但需要高精度、高稳定的空间激光建链,同时,多节点的位置解算对硬件资源也提出了极高的要求。而基于光载GNSS三维基线测量技术对硬件要求低,并可自由组网,有望实现高精度、大范围、任意节点的空间同步。

3 分布式相参雷达性能验证

为了验证分布式相参探测的性能,本文构建了一套基于微波光子技术的宽带分布式相参探测原理验证系统。该系统工作于X波段,具有2发2收的结构。其中,发射单元利用微波光子倍频技术生成瞬时带宽为4 GHz的探测信号,接收单元采用微波光子去斜接收技术对回波信号进行接收处理。待测目标设置为直径为5 mm的螺栓。根据初始参数估计的结果,调整两个雷达单元发射信号的时延和相位,让多个发射波形同时、同相地照射目标,实现发射相参。随后对两单元接收信号进行相参接收,实现收发全相参,从而进一步提升信噪比。

图12为发射相参和全相参模式下雷达去斜接收的结果。在发射相参模式下,回波信噪比较单部雷达提升了5.93 dB;在收发全相参模式下回波信噪比较单部雷达提升了8.82 dB,非常接近理论值6 dB和9 dB。

图12 相参模式下去斜信号的频谱

在相参雷达成像方面,清华大学的研究团队对微波光子分布式相参雷达系统进行了距离多普勒成像的实验验证[19]。在实验中,将三个角反射器以10 cm间隔均匀摆放,分别测试了两个雷达单元在单站模式、发射相参模式及全相参模式下的成像结果。结果显示,在发射相参模式下,回波信噪比有所提升,距离雷达发射机最近的角反射体可以被明显探测到,但另外两个角反射体的成像结果较为模糊。当雷达工作在收发全相参模式时,回波信噪比得到了进一步提升,可在成像结果中清晰分辨三个目标。

4 结束语

本文对分布式相参雷达及其所需的时、空、频、相信号同步技术进行了总结与分析。针对高频段分布式相参雷达系统对时、空、频、相同步精度的高要求,重点探讨了微波光子测量与同步技术。基于光学系统波束细、带宽大、传输损耗低和并行处理等特点,微波光子技术为高精度时、空、频、相同步提供了可行的解决途径。其中,微波光子主/被动稳相传输、微波光子时间同步、高精度激光测距以及光载GNSS三维基线测量等关键技术已在精度和作用距离上展现出了独特优势,可为分布式相参探测,尤其是高频段雷达的分布式相参,提供关键支撑。值得关注的是,随着分布式相参技术在天基、空基、海基等动平台上拓展应用,微波光子技术的高速同步能力也有望发挥重要作用。