基于浮动车轨迹数据的干线信号协调配时优化

杨伟, 沈国栋, 龙光, 钱宇, 丁恒*

(1.安徽省交通规划设计研究总院股份有限公司, 安徽 合肥 230088;2.合肥工业大学 汽车与交通工程学院, 安徽 合肥 230009)

0 引言

随着社会经济的发展,机动车数量的快速增长导致道路网络负担加重,提高交通系统运行效率显得愈发重要。干线协调控制作为城市道路交通管理的一种重要方式,可通过整体协调干线上若干相邻交叉口信号配时,提升道路整体的通行效率,降低总体延误水平。干线协调控制的效果除了受到道路物理参数影响外,也受到通过干线的交通流的动态性的影响。准确并有效获取干线道路的动态交通需求,根据需求调节信号配时显得尤为必要。受限于传统基于感应线圈或视频的断面检测手段只能获取车辆的到达数据,难以利用更精确的车辆轨迹数据实现干线信号的协调优化。

干线协调优化利用绿波交通来提高交通干线的通行能力,对于绿波带宽的优化可以有效提升城市干线的通行效率。文献[1-3]中通过对传统数解法和图解法的改进,以修正绿波带宽的计算方法对干线协调控制进行优化。曾佳棋等[4]针对经典数解法不能确保得到最优解的问题,提出新的改进数解算法,避免重复计算绿时损失,降低了计算量。除了绿波带宽的优化,王昊等[5]为提升临界饱和状态下干线车流通行效率,提出了一种基于冲击波理论的干线双向信号协调控制方法,构建了以干线双向通过量最大化为优化目标的模型。文献[6-8]中对城市干线进行数学建模,通过采集相应交通数据及场景构建,以延误时间等具体指标的优化为目标,通过遗传算法、粒子群算法等对其关键参数进行求解而形成的优化方案,也十分有效。许多科研人员将成果运用于实际案例,推动传统干线协调技术走向成熟,文献[9-10]中分别针对兰州市安宁区区域路网与青岛市珠江路干线的交通状况,论证了其理论可行性。

随着卫星定位及网联通信技术的快速发展,利用网联车动态信息可实时获得车辆轨迹数据,使得通过准确实时的车辆轨迹数据优化干线信号协调控制成为可能。考虑到实时数据的采集对于交通控制的重要作用,越来越多科研人员将实时车辆轨迹数据的分析融入交通控制应用中。Feng等[11]针对单点交叉口形成了2种控制框架,其一就是通过智能车辆的轨迹控制,构建一个以车辆延误为目标函数的动态规划模型。Tang等[12]将基于智能网联车辆技术的大量高分辨率轨迹数据用于交叉路口交通量估计,克服了传统模型驱动方法依赖到达分布和排队规则的假设。文献[13-15]中通过对车辆微观角度轨迹数据的研究分析,提出了基于轨迹数据的交通参数获取方法,对混合车流交通状态、到达率等参数的获取更加准确,为交通控制提供了可能。文献[16-21]中通过对交通参数的建模,将微观车辆轨迹的研究与交通控制相结合,形成车联网环境下更加先进的交通控制方法。通过对车辆微观行为数据的研究,交通控制准确度相比较传统基于历史统计数据的交通控制更加准确、高效,也成为今后发展的主流方向。

通过分析国内外学者对于传统干线协调控制的研究不难发现,传统利用断面流量实现干线协调的相关技术研究已较为深入,但是利用更精细化的轨迹数据解决干线协调控制问题仍处于快速发展阶段。虽然已有学者使用智能网联技术解决干线协调控制问题[11-21],然而其全面普及仍需一定的时间。在当前人工驾驶交通环境下,安装有终端定位设施的浮动车辆也越来越多,如何利用这些浮动车轨迹数据实现干线交通信号协调配时优化是一项非常重要的现实问题,因此,本文考虑浮动车与其他普通车辆混合流的场景,探索干线道路交通流的到达预测及信号配时优化,最后采用实际道路路网数据对本文方法与既有干线协调控制方法进行对比分析。

1 浮动车轨迹数据处理

浮动车数据包括车辆的位置数据与对应时刻、停车状态等。将原始轨迹数据中存在的较长时刻间距内位移较小、相近时刻位移浮动异常、位置信息突变频繁等错误数据剔除之后,根据轨迹数据获取本研究所需的交通参数、自由流车速及预测到达率。

1.1 自由流车速确定

为了确定两相邻路口间路段的自由流车速,在网联环境下,可通过采集大量浮动车辆位置数据,结合采集时间间隔估算出相应路段的平均行程时间,剔除经过停车的车辆后可得到相对准确的自由流车速。具体操作时,可对路口1、2之间时距图进行分析,路段车辆轨迹时距图如图1所示,横轴表示时间,纵轴表示距离,选取其中多组未停车的车辆轨迹,求取平均值,得到路段的平均行程时间,平均行程时间求取公式为

图1 路段车辆轨迹时距图Fig.1 Time distance map of vehicle trajectory in road section

(1)

式中:t为路段平均行程时间;ti为未停车通过2个路口车辆i的行程时间;m为车辆数。

在对浮动车轨迹数据进行处理时,若该车为未停车车辆,计算自由流车速时,通过车辆在路段内第一次与最后一次出现时间差与位置差可确定路段的自由流车速vf。

1.2 基于浮动车轨迹数据的车辆到达率预测

由于本文所提出的干线控制适用于混合车流运行的环境,未掌握全部的车辆运动轨迹信息。为了准确把握干线交通状况,获取交通流参数,本文需要预测网联车辆与普通车辆混合行驶情况下的交通到达率。其基本思想是依据浮动车辆是否有停驶行为,判断浮动车轨迹并预测整个交通流的到达信息[22]。

选取一个周期内最先通过交叉口的浮动车数据,记为浮动车1,选择最后一个通过交叉口的浮动车数据记为浮动车2,混合交通量估计原理如图2所示。图2(a)中,浮动车1与浮动车2经过交叉口时均没有停车行为,表明红灯开启后到浮动车1到达交叉口时其前方队列消散,不足以影响浮动车1的行驶,因此可以根据浮动车1的到达时间计算出前方可能产生排队的车辆数上界,通过浮动车2与浮动车1之间的轨迹计算期间到达车辆数上界,得到车辆到达率。图2(b)中,浮动车1通过交叉口时有停车行为,而浮动车2没有停车,根据浮动车1的停车位置或出发时间,可以计算在它前面排队的车辆数。根据浮动车2的轨迹计算出浮动车1和浮动车2之间可能到达的车辆数上界。结合这些车辆轨迹的信息,可以估算车辆到达的总体数量。图2(c)中浮动车1与图2(b)中行为一致,而浮动车2也发生了停车行为,因此可以根据浮动车2停车位置与出发时间计算前方队列车辆总数,而在浮动车2之后到达的车辆可以根据浮动车2出发时剩余绿灯时间进行估计。

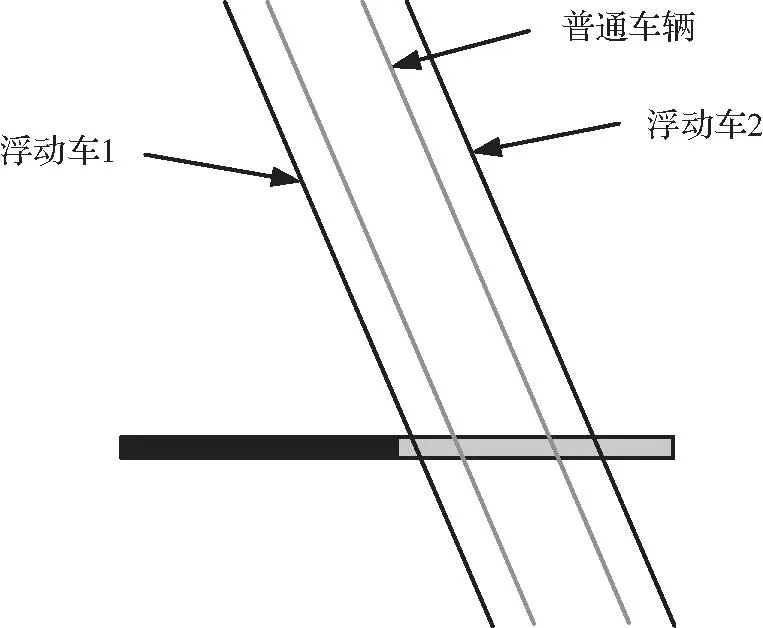
(a) 车辆到达情景1

(b) 车辆到达情景2

(c) 车辆到达情景3图2 混合交通量估计原理Fig.2 Principle diagram of hybrid traffic estimation

利用最大期望(maximum expectation, EM)算法估计式中的车辆到达率P,将其表示为

(2)

式中,若pi=1,pi-1=±1,则红灯启动后浮动车1产生停车现象后,观测到浮动车2发生停车;若pi=2,pi-1=±1,则表示红灯启动后观测到的浮动车通过交叉口未停车;ny,i表示[tf,i-1,tf,i]之内车辆的离开次数,下标z表示不发生停车的浮动车辆;nz,i表示红灯启动后不停车通过交叉口的辆数;py,i表示[tf1,i-1,tf,i]时间内浮动车的离开次数;Pz,i表示红灯启动后不停车通过交叉口的浮动车辆数。

将车流到达看作是一个与时间相关的泊松分布,考虑浮动车轨迹在实际进口道的2种不同运行状态,可计算出车辆到达率的估计值。

2 基于轨迹数据的干线协调控制模型

2.1 干线协调环境及基本参数确定

干线协调优化的基本原理是通过调整相邻交叉口之间绿灯启动时间的时间差,即相位差,来实现绿波交通,处于绿波之间的车辆可连续不断地通过干线多个交叉口。本文提出的基于车辆轨迹数据的干线优化模型,是以减少车辆平均延误为目的。为了方便对模型进行描述,在建立控制模型时,假设以下条件成立:

① 交通流为欠饱和状态,每次绿灯时间结束前,排队状况均能够清空。

② 将黄灯时间划入绿灯时间之中。

③ 保持每个信号交叉口控制相位相序均不变。

④ 每个交叉口协调相位的总延误均可用韦伯斯特延误模型表示。

因为干线各交叉口非关键相位车流量仍然会对干线协调的效果造成影响,所以在形成各交叉口信号配时时,需要考虑到非关键相位车流量的影响[23]。通过上述车辆到达率预测可较为准确地获取交叉口各方向的交通到达率,基于此可对干线各交叉口的基本参数进行确定,具体如下。

① 关键交叉口协调相位有效绿灯时间。

关键交叉口协调相位有效绿灯时间可以表示为

(3)

式中:tge,I是指关键交叉口协调相位有效绿灯时间;C表示协调交叉口公共周期时长;Ls表示关键交叉口总损失时间,其中包括黄灯时间和相位的绿灯损失时间;yI表示关键交叉口主干道流量比最大值;YI表示关键交叉口最大流量比之和。

② 非关键交叉口各相位有效绿灯时间。

非关键交叉口非协调相位最小有效绿灯时间可以表示为

(4)

式中:tr,n表示非协调相位最小有效绿灯时间;Sn表示交叉口i的第n个非协调相位的关键车道饱和流量;qn表示交叉口i的第n个非协调相位的关键车道到达流量;xq表示交叉口进口道饱和度。

因为关键交叉口的协调相位最小有效绿灯时间相较于非关键交叉口协调相位的有效绿灯时间短,所以为了形成最大绿波带,通常在非协调相位的绿灯时间确定后,把余下的有效绿灯时间均分配给协调相位,得到

(5)

式中:tge,i为第i个交叉口的协调相位绿灯时间;L为启动损失时间;N为该交叉口相位总数。

2.2 基于轨迹数据的干线协调控制模型

2.2.1 干线道路下行方向饱和度模型

城市干线中运行的车辆通常在进入协调优化范围之前,会在上游交叉口停车线处形成车队,并以车队形式进入城市干线。在2.1节所假设交通环境及通过2.2节确定的干线协调控制基本参数下,考虑干线行驶车队头车到达交叉口时会遇到以下4种情形:

① 第一辆车到达下一交叉口时遇见红灯,红灯剩余时间为tsrs,前方无排队车辆。

② 第一辆车到达下一交叉口时遇见红灯,红灯剩余时间为tsrs,前方有排队车队长度为lrw。

③ 第一辆车到达下一交叉口时遇见绿灯,绿灯剩余时间为tsgs,前方无排队车辆。

④ 第一辆车到达下一交叉口时遇见绿灯,绿灯剩余时间为tsgs,前方有排队车队长度为lgw。

以上情形分别如图3(a)、图4(a)、图5(a)、图6(a)所示,基于此4种情形建立模型。

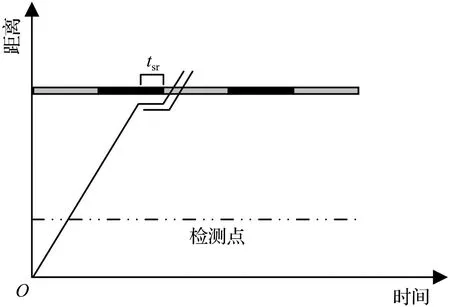
(a) 首车到达场景示意图

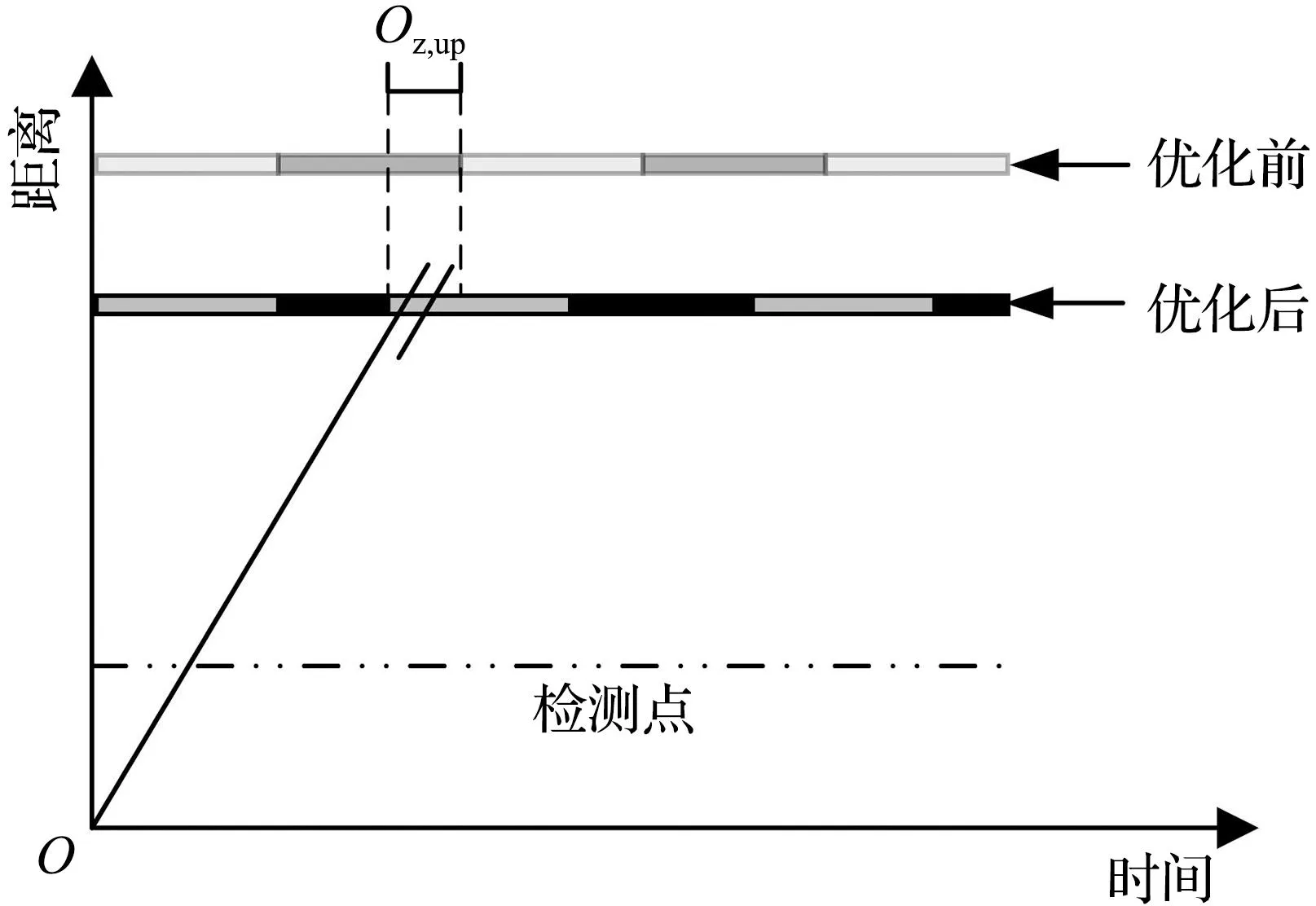
(b) 优化后的场景图3 情形1车辆运动轨迹示意图Fig.3 Schematic diagram of the vehicle trajectory of scenario 1

(a) 首车到达场景示意图

(b) 优化后的场景图4 情形2车辆运动轨迹示意图Fig.4 Schematic diagram of the vehicle trajectory of scenario 2

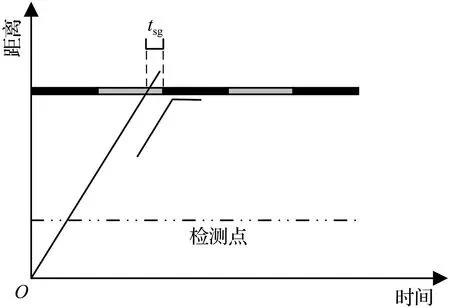
(a) 首车到达场景示意图

(b) 优化后的场景图5 情形3车辆运动轨迹示意图Fig.5 Schematic diagram of the vehicle trajectory of scenario 3

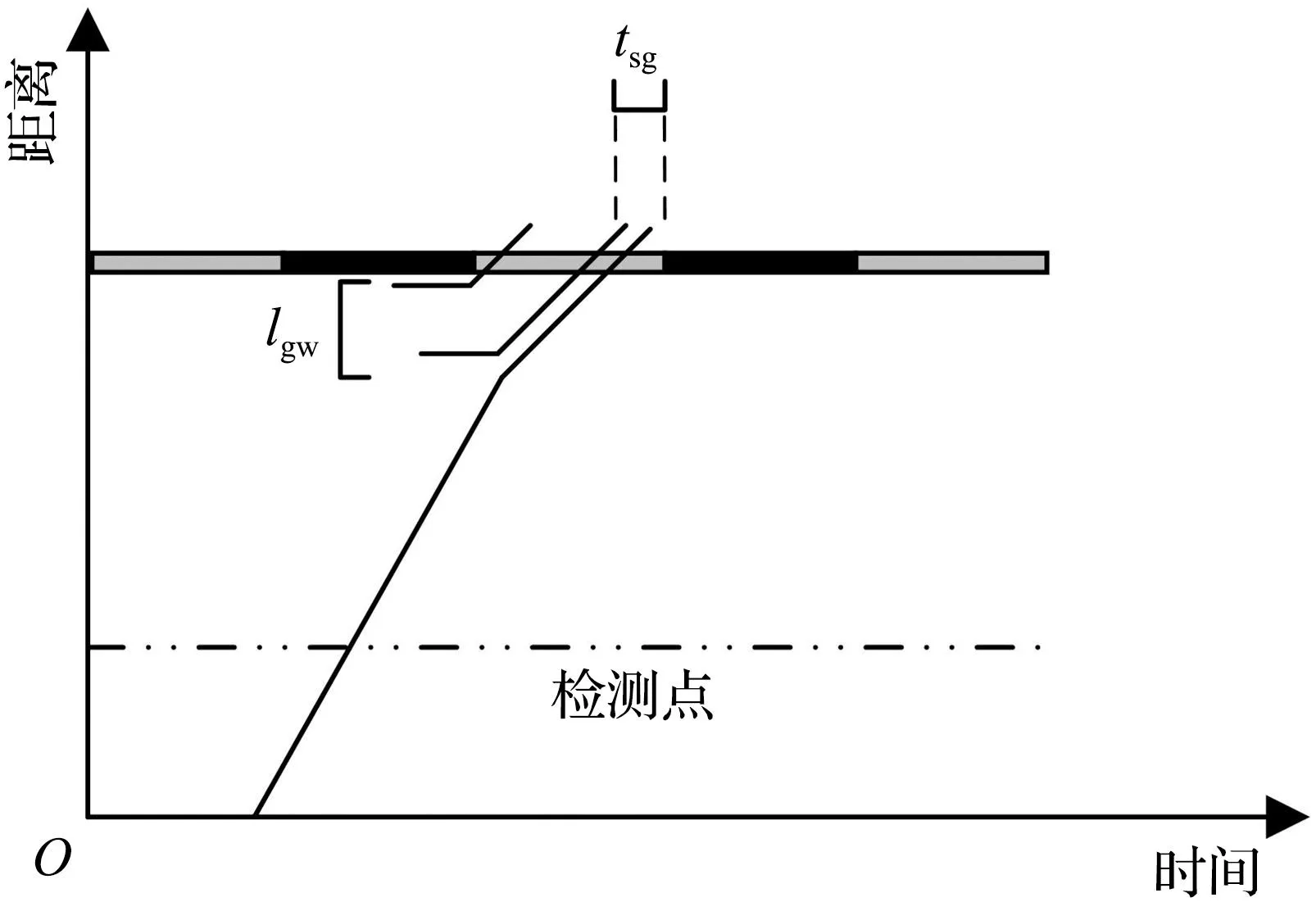
(a) 首车到达场景示意图

(b) 优化后的场景图6 情形4车辆运动轨迹示意图Fig.6 Schematic diagram of the vehicle trajectory of scenario 4

情形1:

因为第一辆车辆到达时,前方显示为红灯,考虑最近可优化时间,此时可将绿灯开启时刻前移Oz,up个单位,所以可将前移后的进口道饱和度表示为

(6)

式中:tc是原计划绿灯开始时刻;qi,up为上行车队到达率;si是第i个交叉口进口道饱和流率;tge,i是协调相位有效绿灯时间。

轨迹优化后的图形如图3(b)所示。此时,由于绿灯提前开启,进口道积累的排队车辆提前进行释放,因此增加了进口道周期内的饱和度。

情形2:

此时将相位差前移Oz,up个单位,因此可将前移后的进口道饱和度表示为

(7)

式中:ts为队伍消散时间。

轨迹优化后的图形如图4(b)所示。

情形3:

由于此时停车线前排队长度为0,同时为保证车队车辆全部顺利通过,因此可将相位差后移Oz,up个单位,后移后的进口道饱和度表示为

(8)

轨迹优化后的图形如图5(b)所示。

情形4:

此时将相位差前移Oz,up个单位,因此可将前移后的进口道饱和度表示为

(9)

轨迹优化后的图形如图6(b)所示。

综合以上4种情形,协调交叉口i进口道饱和度计算公式表示为

(10)

2.2.2 干线道路上行方向饱和度模型

根据Oz,up+Oz,down=C得Oz,down=C-Oz,up,与情形1—4中推导公式相似,区别在于此处将下行方向车辆轨迹数据换成上行方向轨迹数据,同时将Oz,down=C-Oz,up代入上述4个公式中。

情形1中考虑上行相位差与下行相位差之间的关系以及前方交叉口配时参数,将饱和度表示为

(11)

式中qi,down表示下行车队到达率。

情形2中的进口道饱和度可表示为

(12)

情形3中的进口道饱和度可表示为

(13)

情形4中的进口道饱和度可表示为

(14)

2.2.3 干线协调控制目标函数

在车辆分布已知情况下,以韦伯斯特延误模型[22]为基础构建的总延误模型为

(15)

式中:λ为交叉口协调相位的绿信比;x为交叉口进口道饱和度。

引入变量α、β、χ、δ,当情形1成立时,α=1,反之α=0;当情形2成立时,β=1,反之β=0;当情形3成立时,χ=1,反之χ=0;当情形4成立时,δ=1,反之δ=0。

综上,第i个交叉口的下行方向车辆延误公式可以表示为

Di,x=αDi,1+βDi,2+χDi,3+δDi,4,

(16)

在此基础上得到干线上第i个交叉口车辆的总延误公式为

Di=Di,x+Di,s,

(17)

式中Di,s表示第i个交叉口上行方向车辆延误。

以干线道路所有交叉口总延误最短为优化目标,目标函数为

(18)

s.t. 0≤Oz,up≤C,

式中R表示干线交叉口数量。

2.3 干线协调控制参数求解

干线协调的信号周期利用估计的车辆到达率采用传统配时方法较易获得,协调配时优化的关键参数实际上是干线道路协同方向的相位差。本模型选取遗传算法作为求解算法,以式(18)延误模型为适应度函数,各路口干线协调相位差作为自变量。通过对自变量的编码迭代,计算干线协调的最优相位差,并应用到模型之中。该方法准确高效,相比较同类算法不易陷入局部最优解。具体求解流程如图7所示,步骤如下。

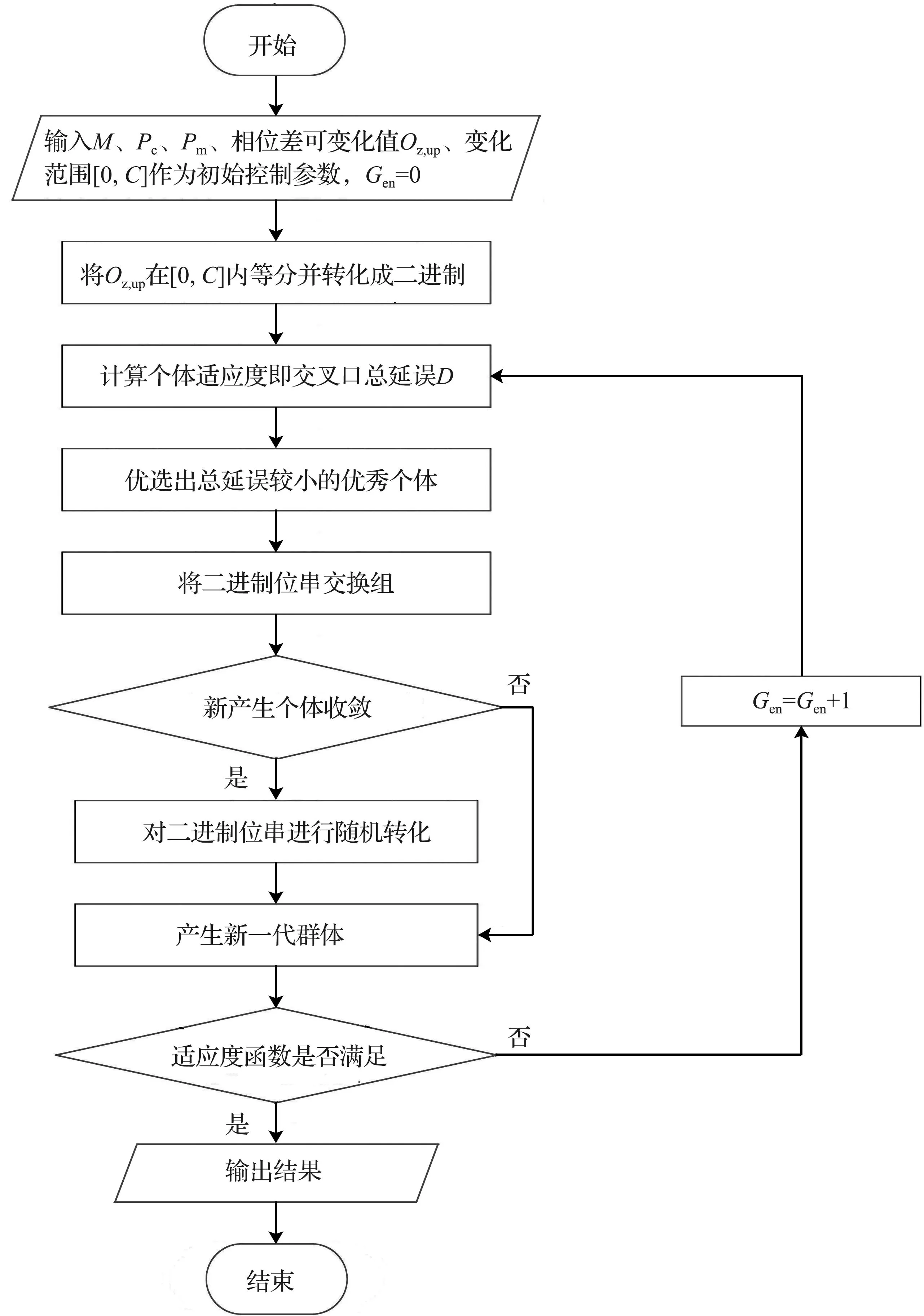
图7 算法流程Fig.7 Algorithm flow chart

步骤1设置群体大小为M,交叉概率为Pc,变异概率为Pm,将相位差的可变化值Oz,up在范围[0,C]内等间距分成M份,并转化为二进制数作为位串,全部位串组成种群。

步骤2将公式(18)作为适应度函数,将转化为二进制后的Oz,up作为个体,计算D即干线交叉口总延误,D越小则适应程度越高。

步骤3对种群中不同的Oz,up值按照适应程度进行筛选,优选出个体按照步骤1中交叉概率Pc和变异概率Pm进行位串交换组合等操作。

步骤4若种群通过交换组合新产生个体适应度函数收敛,则继续步骤5,否则跳至步骤6。

步骤5对位串中某一位二进制数进行随机转化,防止优化过程中陷入局部最优解。

步骤6产生新一代种群。

步骤7计算适应度函数是否满足,若满足则跳至步骤8,否则跳至步骤2。

步骤8解码输出。

3 实例分析

3.1 现状配时及交叉口关联度分析

以合肥市黄山路(香樟大道至科学大道)段为例,交叉口分布如图8所示。路段包含黄山路-香樟大道、黄山路-天柱路、黄山路-科学大道3个交叉口。《美国交通控制手册》中提供的交叉口关联度计算模型[23]为

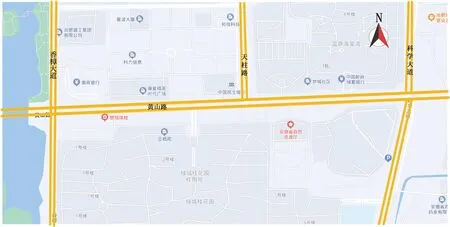
图8 黄山路干线各交叉口分布示意图Fig.8 Diagram of the distribution of each intersection of Huangshan Road mainline

(19)

式中:I为交叉口群间的关联度;w为上游交叉口车辆驶入路段分支数;t为路段行程时间,min;qmax为上游交叉口主线直行最大流量;qi表示第i个交叉口主线直行流量。可以求得黄山路段(香樟大道至科学大道)西至东方向两相邻交叉口之间的关联度分别为0.699、0.564,东至西方向两相邻交叉口之间关联度分别为0.631、0.532,均大于0.5,因此该3个交叉口可以采取协调控制。

本文所获取数据当天干线各主要交叉口配时方案如下。在处理现有配时方案时,为了便于分析,将原相位重新分类,只保留协调相位和非协调相位形式。由于研究方向自西向东,因此将04:30—07:15、09:00—16:30、19:00—22:00时段内,黄山路-香樟大道路口西直左相位作为协调相位。具体配时方案见表1,其中表中数据为“[绿灯时长,红灯时长]”。

表1 黄山路干线主要路口测试时段原配时方案Tab.1 Original timing scheme for test periods at the main intersections of the Huangshan Road arterial

3.2 合肥黄山路干道与车辆轨迹数据分析

采取上文提到的时距图分析方法对黄山路干线浮动车轨迹进行提取,黄山路干线在选取的各时间段内车辆轨迹的时距图(由于车道未处于封闭状态,中途有车辆离开干线检测范围,同时也有外部车辆临时加入,因此部分车辆轨迹只有局部被检测)如图9所示。图9中显示了车辆从黄山路-玉兰大道交叉口经过黄山路-香樟大道交叉口、黄山路-天柱路交叉口、黄山路-科学大道交叉口之间的线路,经干线信号控制,在时距图中产生多条与时间轴接近平行的线,即交叉口处产生停车。图9中交叉口1为黄山路-香樟大道交叉口;交叉口2为黄山路-天柱路交叉口;交叉口3为黄山路-科学大道交叉口。

图9 各时段黄山路干线浮动车轨迹时距图Fig.9 Time distance map of floating vehicle trajectory of Huangshan Road mainline for each time period

通过时距图轨迹的积累,可以求得各时段黄山路干线各路段行程时间、停止车辆数、停止车辆时间等交通参数,结合第2节所述到达率估计方法,估计各交叉口相应时段各进口道之间的估计到达率见表2至表5。其中,黄山路与天柱路交叉口是一个T形交叉口,因此在信号配时时,仅考虑从西向东行驶时,由西进口道产生的左转交通流,按一定比例选取数值。另外,因右转为常绿状态,故在对交通量信息采集时,同时结合上文所述各交叉口进口道信息,不对各交叉口右转车辆进行计算。

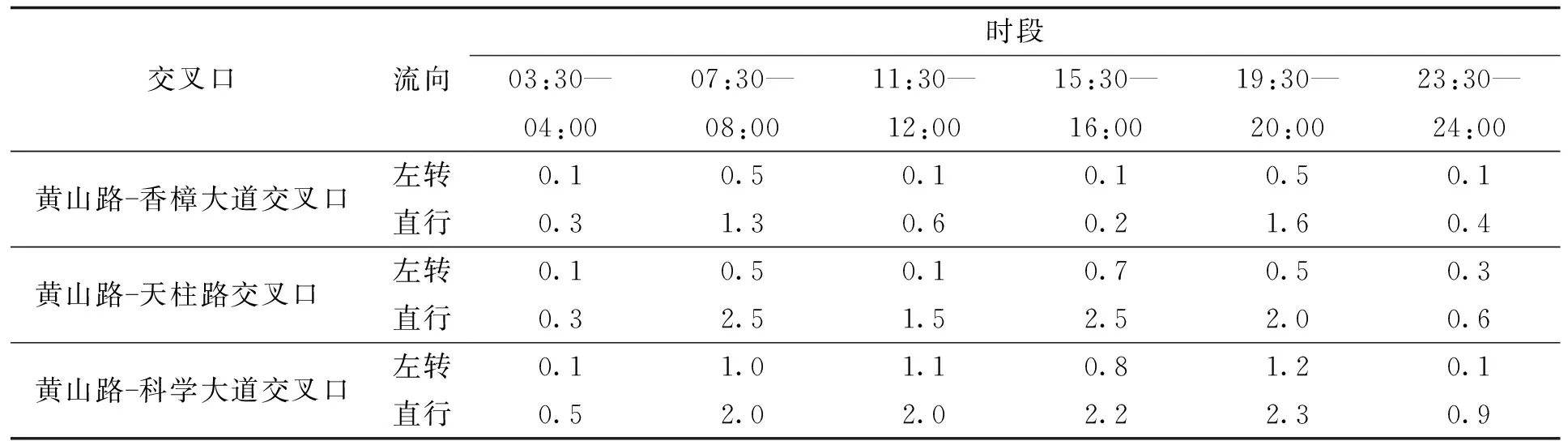
表2 黄山路干线主要路口自西向东方向测试时段估计到达率Tab.2 Estimated arrival rate of the main intersection of Huangshan Road arterial from west to east direction during the test period veh/s

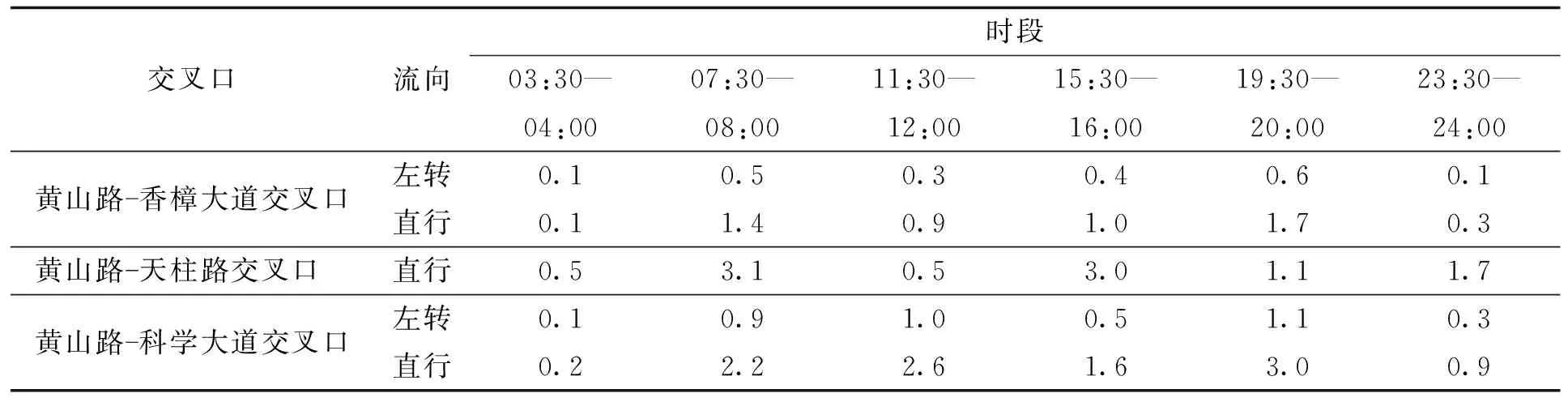
表3 黄山路干线主要路口从东向西方向测试时段估计到达率Tab.3 Estimated arrival rates at the main intersections of the Huangshan Road arterial from east to west during the test period veh/s

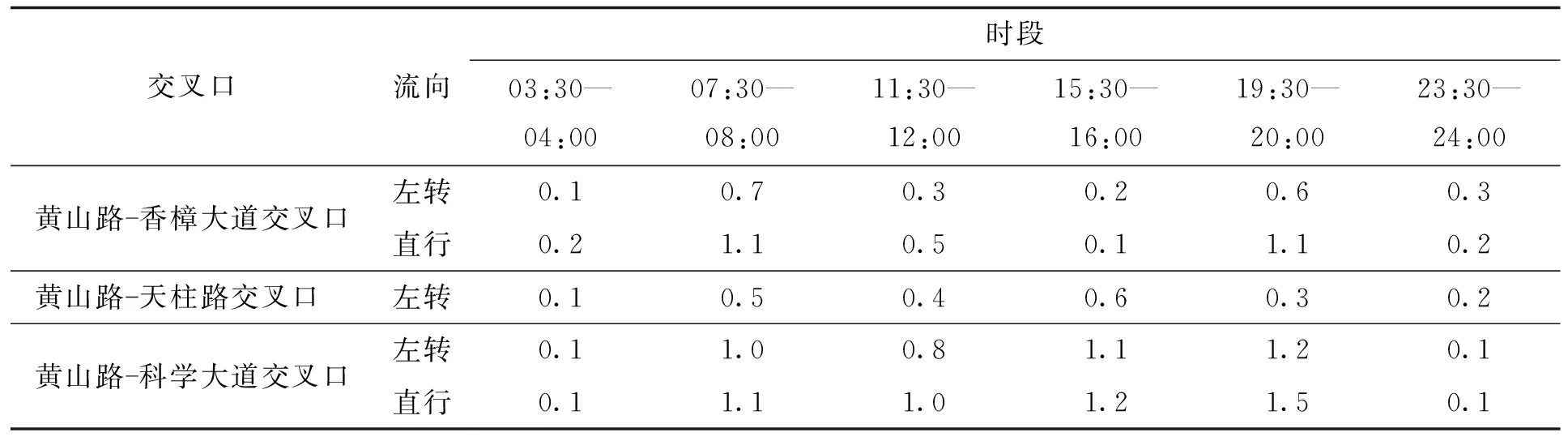
表4 黄山路干线主要路口从北向南方向测试时段估计到达率Tab.4 Estimated arrival rate at the main intersection of Huangshan Road arterial from north to south direction during the test period veh/s

表5 黄山路干线主要路口从南向北方向测试时段估计到达率Tab.5 Estimated arrival rates at the main intersections of the Huangshan Road arterial from south to north during the test period veh/s

考虑每个路口有一定车流驶离黄山路干线,为了确保数据尽可能准确,对交通量进行估计的时候分路段进行估计。在获得估计的平均到达率后,依据泊松分布形成道路上车辆到达的空间分布,并通过第2节所示方法进行干线协调控制参数的确定。计算得到的配时方案见表6。

表6 黄山路干线主要路口测试时段配时方案Tab.6 Timing scheme for test periods at major intersections on the Huangshan Road arterial

考虑行人过街时间,故每个交叉口周期时长需小于180 s。基于此进行优化相位差的计算。

3.3 仿真分析

本文通过对比无干线协调控制方案、传统图解法优化方案以及基于轨迹数据的干线协调优化方案,提取1 d内6个不同时段的轨迹数据,对干线内的车辆平均延误进行计算,得到的平均延误见表7,其中的方法1、2和3分别代表的是无干线协调控制、传统图解法控制以及基于轨迹数据优化控制的平均延误与总能耗对比(本文中所使用的能耗表示的是燃油车的耗油量),对比无干线协调控制方案,传统图解法和基于干线轨迹数据的优化方案的平均延误均有较大程度的缩短,此外,基于轨迹数据的优化方案在传统图解法的基础上有较为明显的优化效果。

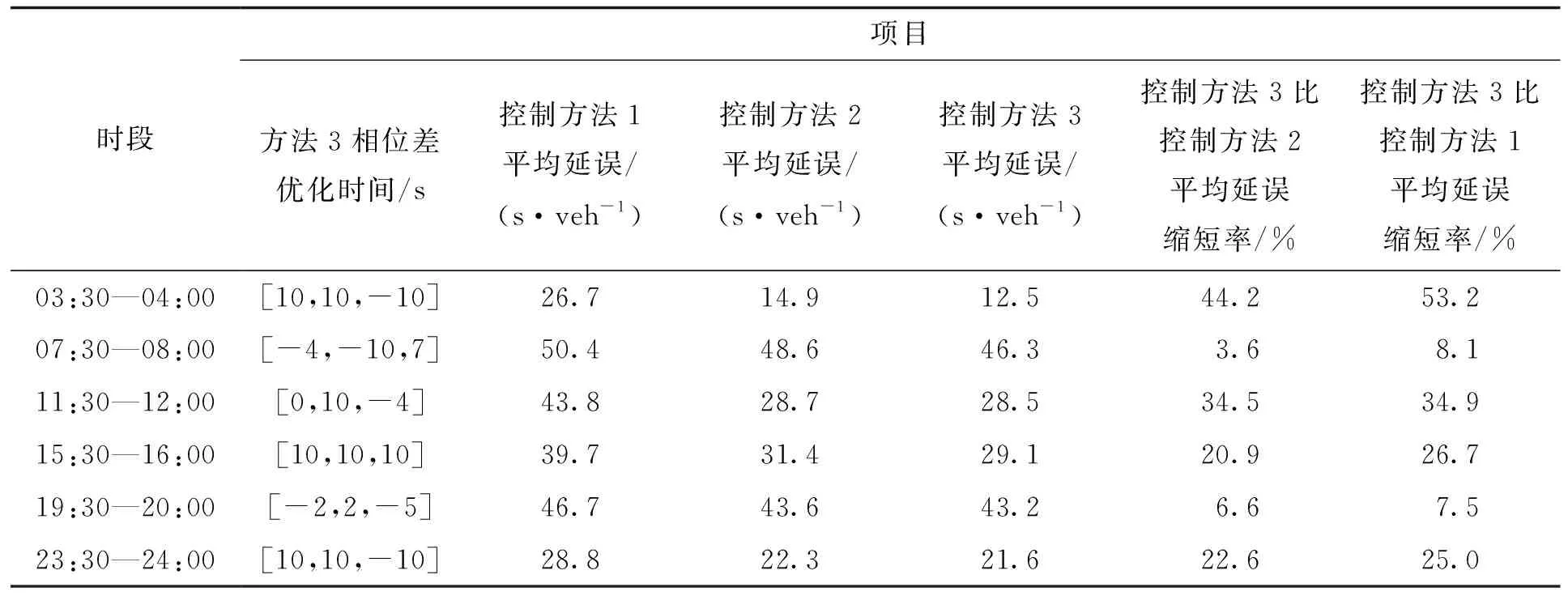
表7 相位差优化与前后平均延误结果Tab.7 Phase difference optimization and average delay results before and after

优化前后黄山路干线总平均延误对比如图10所示。由图10可知,本文所研究的黄山路干线中3个交叉口无干线协调控制时的平均延误总体上长于传统图解法和基于轨迹数据的干线协调优化方法优化后的平均延误,而基于轨迹数据的干线协调优化方法所产生的平均延误总体上短于传统图解法所产生的平均延误,优化效果在平峰时更为显著,在03:30—04:00时段基于轨迹数据的干线协调方案产生的平均延误较无干线协调时更是缩短了53.2%,结果证明本文提出的优化方案十分有效。

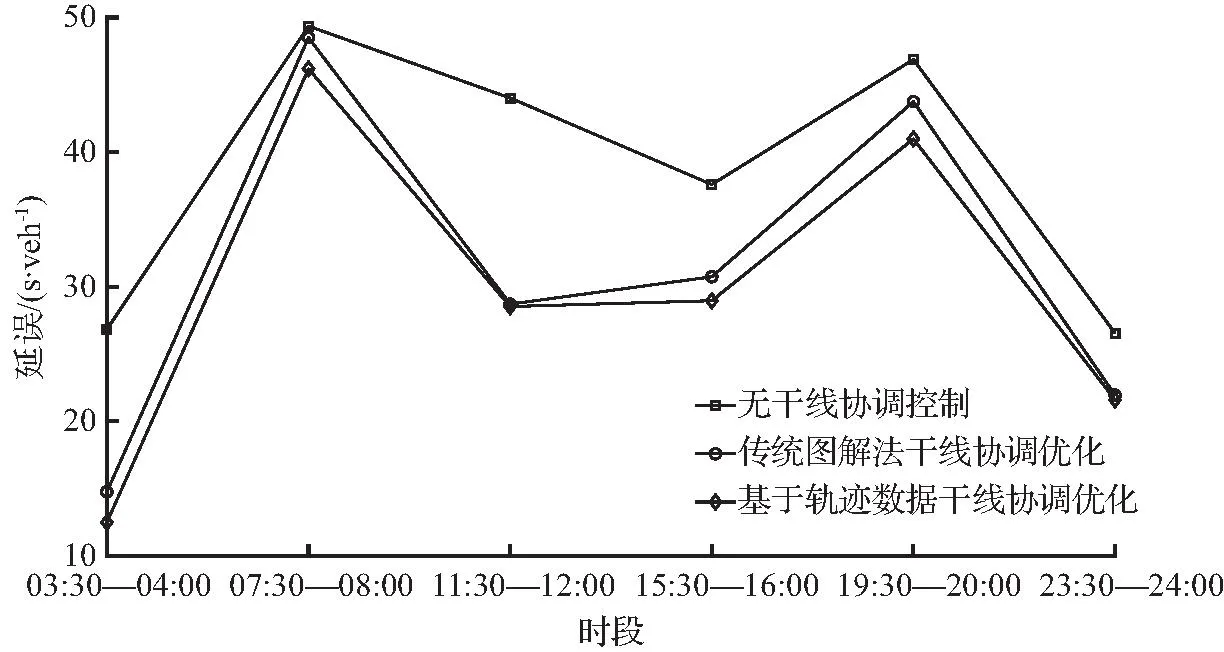
图10 优化前后黄山路干线总平均延误对比Fig.10 Comparison of the total average delay of Huangshan Road trunk line before and after optimization

干线道路内车辆运行的能耗大小是评价模型优化效果的重要指标,本文选取30 min内黄山路干线车辆运行的总能耗为评价优化效果的指标,结合上文所选各时段的交通数据,根据参考文献[24]中所描述能耗计算方法对模型进行评价。

仿真按照表2至表5,选择其中午高峰时段(选取11:30—12:00时段)以及平峰时段(选取15:30～16:00时段)的到达率以及配时信息展开,总仿真时长为30 min,以周期为单位对干线范围内的总车辆能耗进行计算。结果表明,仿真周期经过12周期时,高峰期11:30—12:00时段无协调控制的干线内总车辆能耗为2 464.8 L,通过传统图解法优化后的总能耗为1 636.9 L,通过本文所述基于轨迹数据干线相位差优化方法优化后的总车辆能耗为1 636.5 L。相较于无协调控制,本文所述基于轨迹数据干线相位差优化方法能耗降低了33.6%。与传统图解法干线协调控制相比,本文提出的方法总能耗降低了0.02%。结果表明,在高峰时期本文所提出的优化方法对交通能耗的降低效果不明显。平峰期15:30—16:00时段无协调控制的干线内总车辆能耗为2 657.1 L,通过传统图解法优化后的总能耗为2 119.3 L,通过本文基于轨迹数据干线相位差优化方法优化后的总车辆能耗为2 024.4 L,本文所提出的方法较无协调控制时的总车辆能耗降低23.8%,比传统图解法优化总车辆能耗降低4.5%。仿真时间内干线总车辆能耗变化如图11所示,仿真所得的相位差优化前后干线总能耗结果见表8。

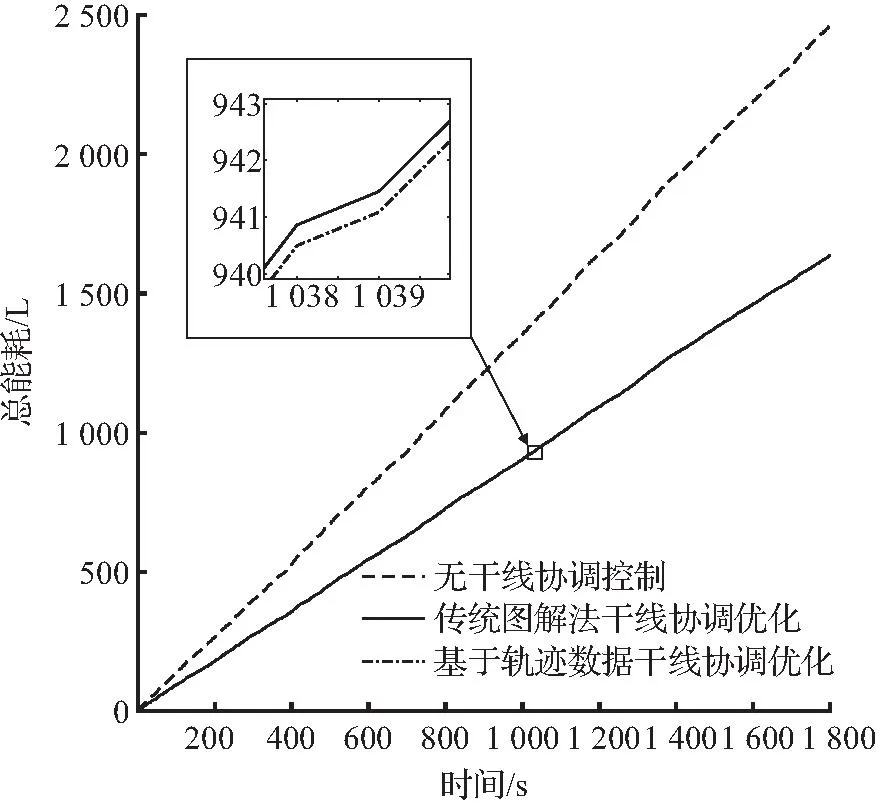
(a) 高峰时段

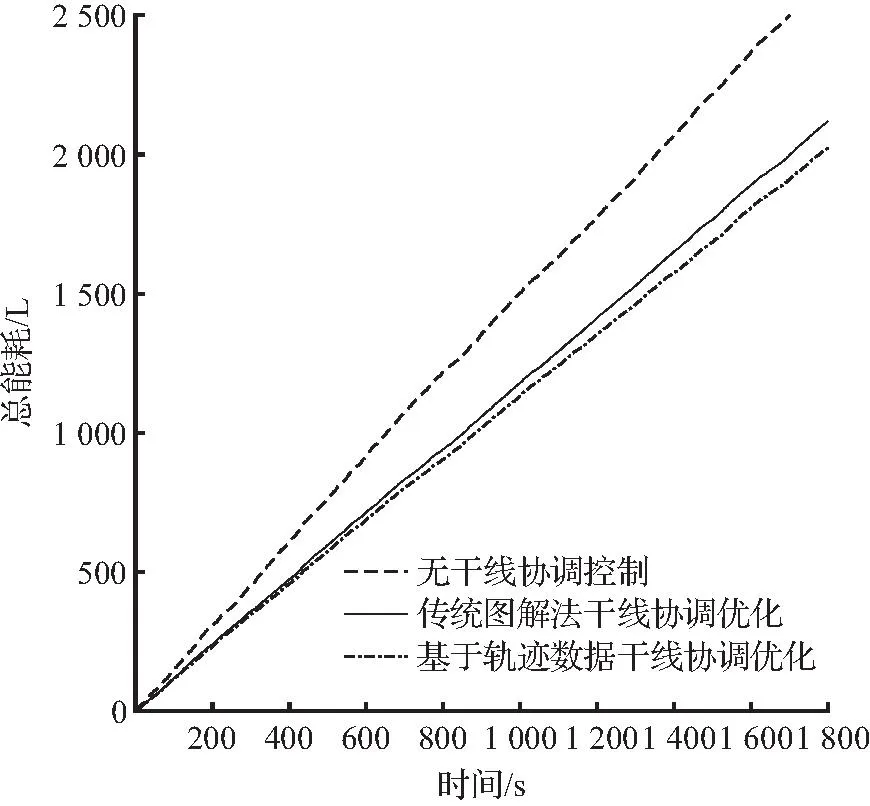
(b) 平峰时段图11 三种配时方案下黄山路干线总交通能耗Fig.11 Total traffic energy consumption of Huangshan Road trunk line under three timing schemes

表8 相位差优化前后干线总能耗结果Tab.8 Total energy consumption results of trunk line before and after phase difference optimization

4 结论

本文中基于车辆轨迹数据建立的干线协调控制相位差优化模型,对干线上各交叉口信号参数实时更新,可在较短时段内对相位差更新优化,提高了干线交通的通行能力,缩短了车辆的平均延误,减少了总能耗。研究结果表明:

① 基于轨迹数据建立的干线协调控制优化模型,可较好地把握城市干线道路的基本交通状态,更加方便、准确地获取交通参数,以供信号协调优化。

② 本文中提出的干线协调优化模型对非高峰时段的优化效果比高峰时段更好。

③ 本文中提出的基于轨迹数据的干线协调控制模型可有效缩短车辆交通干线中行驶所产生的延误,同时可有效减少干线中的车辆总能耗。

本文中对城市干线协调控制优化方法进行了分析,在实际路网中,非机动车和行人影响较大,本文在处理交通量时,未考虑行人及非机动车的影响,下一步研究将着重于行人及非机动车对车流影响模型。同时,本文中提出的干线协调优化模型是以车辆总延误为优化指标,由于可反映运行效率的指标众多,包括交叉口服务水平、最佳饱和度、停车次数等,如何建立更加准确的多指标目标函数控制模型,也值得进一步研究。