多巴胺能神经元模型的分岔分析与同步研究

林心怡, 刘深泉, 宋健

(华南理工大学 数学学院, 广东 广州 510640)

0 引言

神经元是神经系统最基本的结构和功能单位,其不同放电模式对应着神经元不同的信息编码方式。利用分岔理论研究神经元模型的动力学性质[1],被认为是一种广泛有效的方法。近年来,运用分岔理论,刘深泉等[2]、Wang等[3]研究了呼吸神经元模型和胰腺β细胞模型的动力学性质和放电活动。江小芳[4]研究了多巴胺能神经元模型的动力学性质,讨论了单簇内峰数目的变化规律。Zhan等[5]研究了垂体细胞的动力学性质。在神经系统中,耦合的同步性影响着神经元传输信息的效率,许多学者针对耦合系统同步性展开研究。杨永霞等[6]研究了化学耦合Pre-BötC神经元模型的同步转迁规律。杨腾云等[7]研究了电磁影响下环状连接耦合神经元系统的同步转迁。对于不同的神经元模型,耦合连接方式、耦合强度及参数对神经元集体放电活动起到不同的调节作用,因此耦合神经元的放电模式与同步转迁规律是一个值得研究的问题。

多巴胺是大脑中含量最丰富的神经递质,调控着多种生理机能和机体活动,参与了哺乳动物大脑的激励、快乐、运动、学习强化等过程,并且与帕金森综合征[8]、精神分裂症[9]、药物成瘾[10]等疾病有关。释放多巴胺的神经细胞,被称为多巴胺能神经元,主要集中在中脑区域。多巴胺能神经元的活动影响细胞外多巴胺浓度的水平和其靶区血氧水平依赖功能磁共振成像的信号,例如,用频率40 Hz电刺激多巴胺能神经元比频率10 Hz更有效地提高大鼠纹状体的多巴胺胞外浓度[11]。

在不同的条件下,多巴胺能神经元呈现出不同的振荡模式。在活体[12]和离体[13]实验中,阻断小电导钙激活钾(small conductance calcium activated potassium, SK)通道会增加簇节律发放的趋势,这些簇通常以去极化型阻断结尾,与长期服用抗精神病药物的大鼠呈现的簇放电行为类似。在许多簇发放数学模型中,慢振荡去极化期间簇的峰出现,而不发放的簇间间隔比簇内峰峰间距更超级化,这类簇通常被称作方波簇[14]。而这里所说的以去极化型阻断结尾的簇是一类反常簇,其特点是静息状态的簇间间隔比峰峰间距观察到的膜电位更去极化。由Yu等[15]提出的多巴胺能神经元模型,能够抓住多巴胺能神经元由SK通道阻断介导该反常簇行为这一特性,本文的工作就是在此模型的基础上展开。

文献[15]提出的多巴胺能神经元模型虽然能够很好地模拟多巴胺能神经元的生物特性,但它是一个13维的非线性动力系统,直接研究有很大的困难,因此,本文考虑对该模型降维,通过3个降维步骤得到一个能够保持原模型放电特性的四维简化模型,通过研究简化模型的动力学性质,增加对多巴胺能神经元模型由特定参数介导的反常簇行为的了解。本文首先通过单参数分岔和双参数分岔,研究简化模型在不同参数变化下的放电行为和分岔结构,并计算第一Lyapunov系数判断生成极限环的稳定性。其次分别构建电突触和化学突触下耦合多巴胺能神经元模型,研究模型参数对耦合神经元放电特性的影响和同步状态转迁过程,得到模型实现耦合同步的条件。

文献[15]提出的多巴胺能神经元模型的描述如下:

(1)

电流IK,ERG为内向整流钾电流,用下列2个微分方程描述:

式中:i表示ERG关闭的比例;αo、βo、αi、βi表示反应速率,αo=0.003 6exp(0.075 9V),βo=1.252 3×10-5exp(-0.067 1V),αi=91.11exp(0.118 9V),βi=12.6exp(0.073 3V)。

钙离子的平衡满足方程为

式中:ρCa为钙离子浓度,mmol/L;fCa=0.018,是无缓冲自由钙的比例;F是法拉第常数;d为细胞直径;ICa,p表示被排出的钙离子,其被模型化为一个非生电泵:ICa,p=ICap,max/(1+0.000 5/ρCa),其中ICap,max=11 μA,该模型其余参数取值见文献[15]。

1 模型降维

文献[15]构建的多巴胺能神经元模型(1)是一个具有13维的高维复杂动力系统,对这样高维的系统进行动力学分析是非常困难的,下面考虑对原模型降维,研究降维得到简化模型。

步骤1基于Kepler等[17]提出的降维方法,考虑将m、p、q1、q2、l、mH这6个门控变量的表达式用其稳态函数替代,并调整参数值使该步降维后的电位发放特性与原模型一致,各变量的稳态函数见文献[15]。

步骤2通过变量与膜电位的相图,发现变量o、i与膜电位V密切相关,如图1(a)、图1(b)所示,蓝色曲线为变量间相图(图1红色曲线为拟合曲线)。通过曲线拟合得到变量o、i关于膜电位V的表达式为

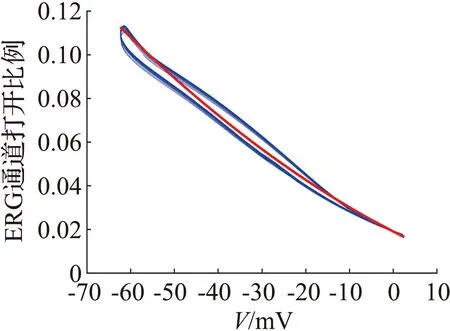
(a) 变量o与V的拟合曲线

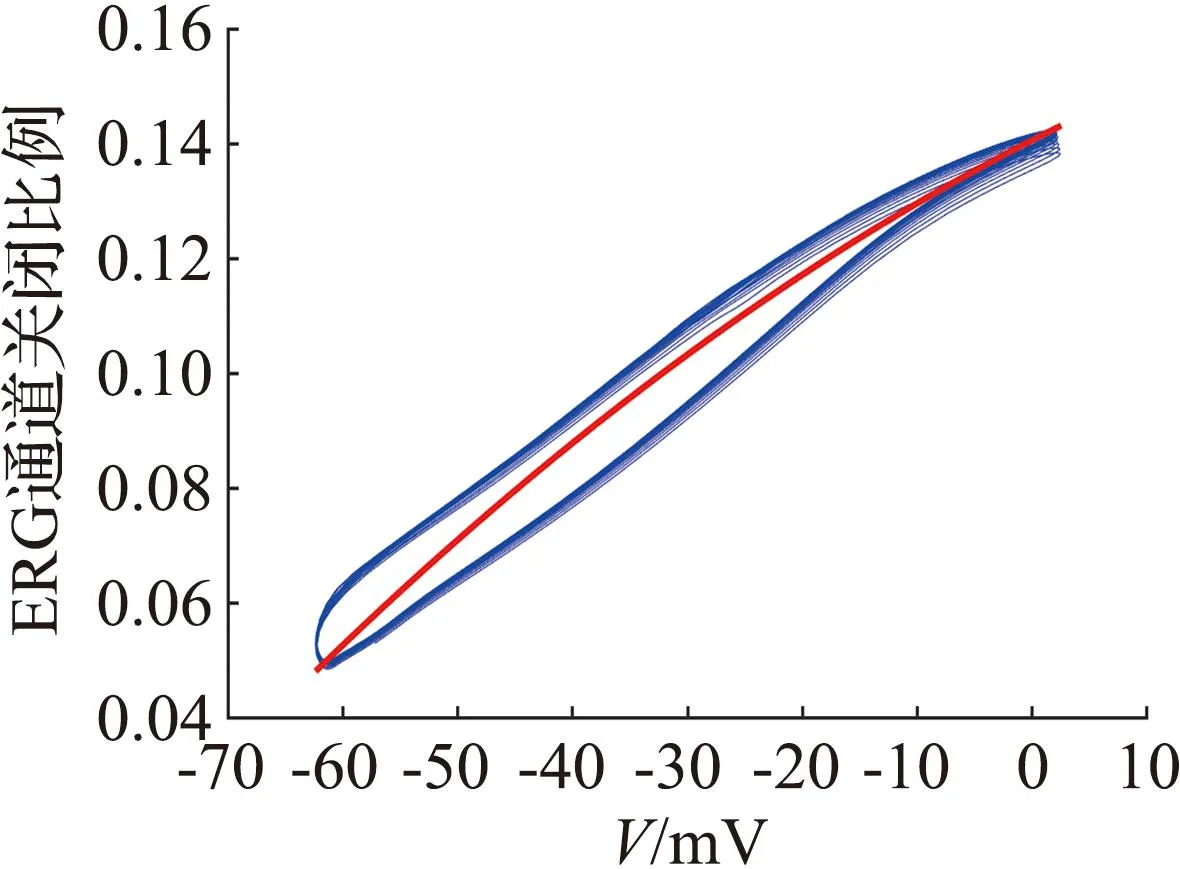
(b) 变量i与V的拟合曲线

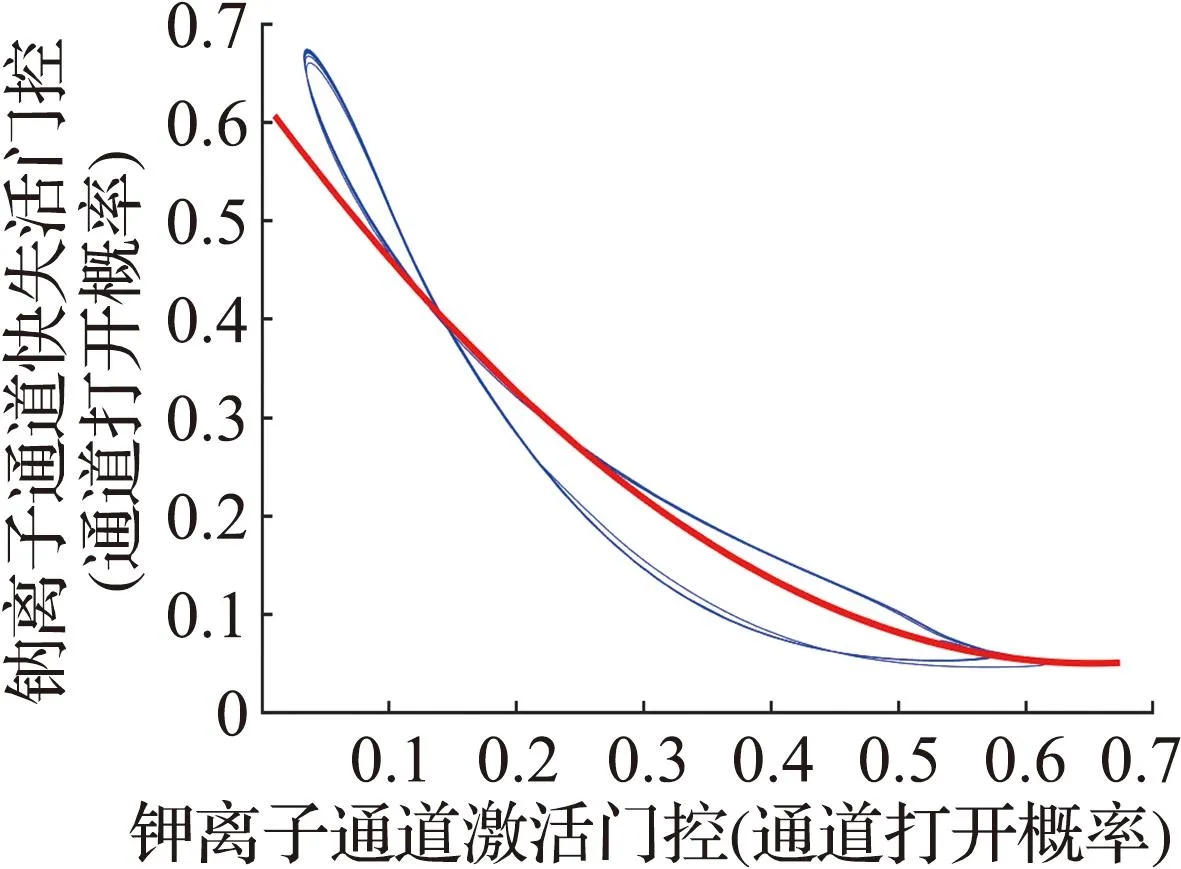
(c) 变量h与n的拟合曲线图1 模型(1)中相关变量相图Fig.1 Relevant variable phase diagram in model (1)

o=7.505×10-6V2-0.001 03V+0.019 11,
i=-7.371×10-6V2+0.001 022V+0.140 6。

(2)

步骤3通过观察剩余变量与门控变量n之间的相图,发现门控变量h与n之间有较强相关性,如图1(c)所示,通过曲线拟合得到变量h关于n的表达式为

h=1.35n2-1.76n+0.624 2。

(3)

通过上述3步降维过程,得到一个四维简化多巴胺能神经元模型,模型方程如下所示:

(4)

除降维过程中替换的门控变量表达式和调整的参数值外,该模型中各电流和时间常数的表达式与原模型相同,且其余参数取值与原模型保持一致,详见文献[15]。

为了使降维后模型(4)的放电特性与原模型(1)一致,调整参数值Vk=-80 mV,gNa=5 700 μS/cm2,gK,A=1 700 μS/cm2,ICap,max=12 μA,gK,DR=500 μS/cm2,其他参数值保持不变。原模型(1)和简化模型(4)的放电比较如图2所示。从图2可见,降维得到的四维简化模型的放电特性与原模型几乎相同,通过阻断SK电流也能使模型出现去极化型反常簇行为,如图2(d)所示。综上,本文通过降维得到的模型是可行的。

(a) 原模型的峰发放

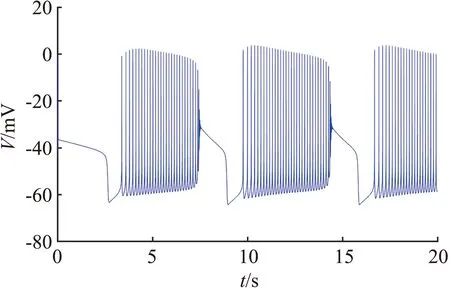
(b) 原模型的簇发放

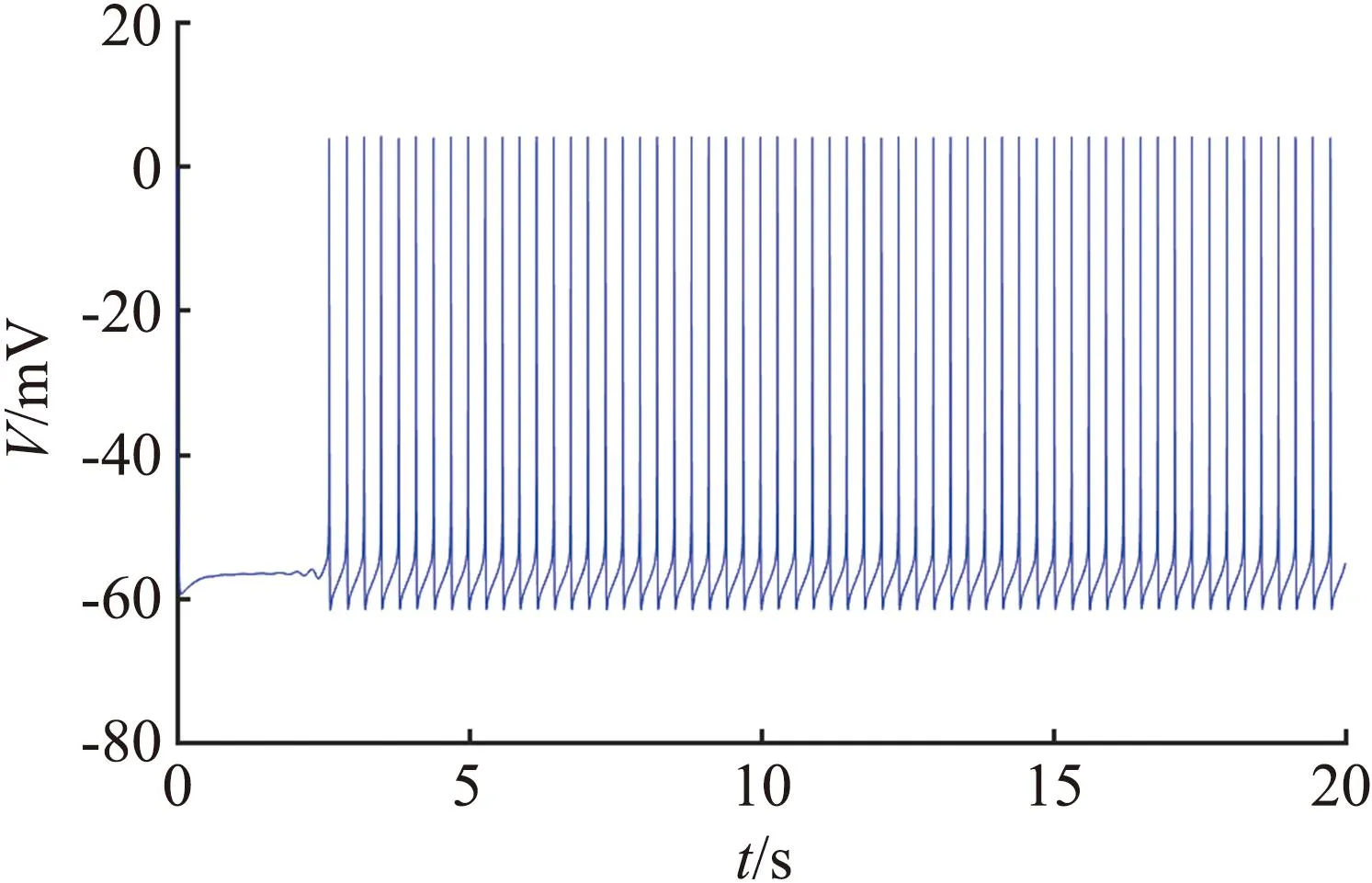
(c) 简化模型的峰发放

(d) 简化模型的簇发放图2 原模型(1)和简化模型(4)的放电比较Fig.2 Potential comparison of original model (1) and simplified model (4)

2 分岔分析

2.1 单参数分岔分析

IK,SK是依赖于钙的小电导钾电流。在生理实验中,阻断该电流会增加反常簇节律放电的趋势,与长期服用抗精神病药物的大鼠体内出现的节律放电类似。本模型通过改变电导gK,SK的值,也可以使得神经元实现簇发放与峰发放之间的转迁。为了更深入地了解gK,SK对神经元节律放电的影响,将gK,SK作为分岔参数,刺激电流Istim与电导gK,SK的单参数分岔与峰峰间距(ISI)分岔比较如图3所示。

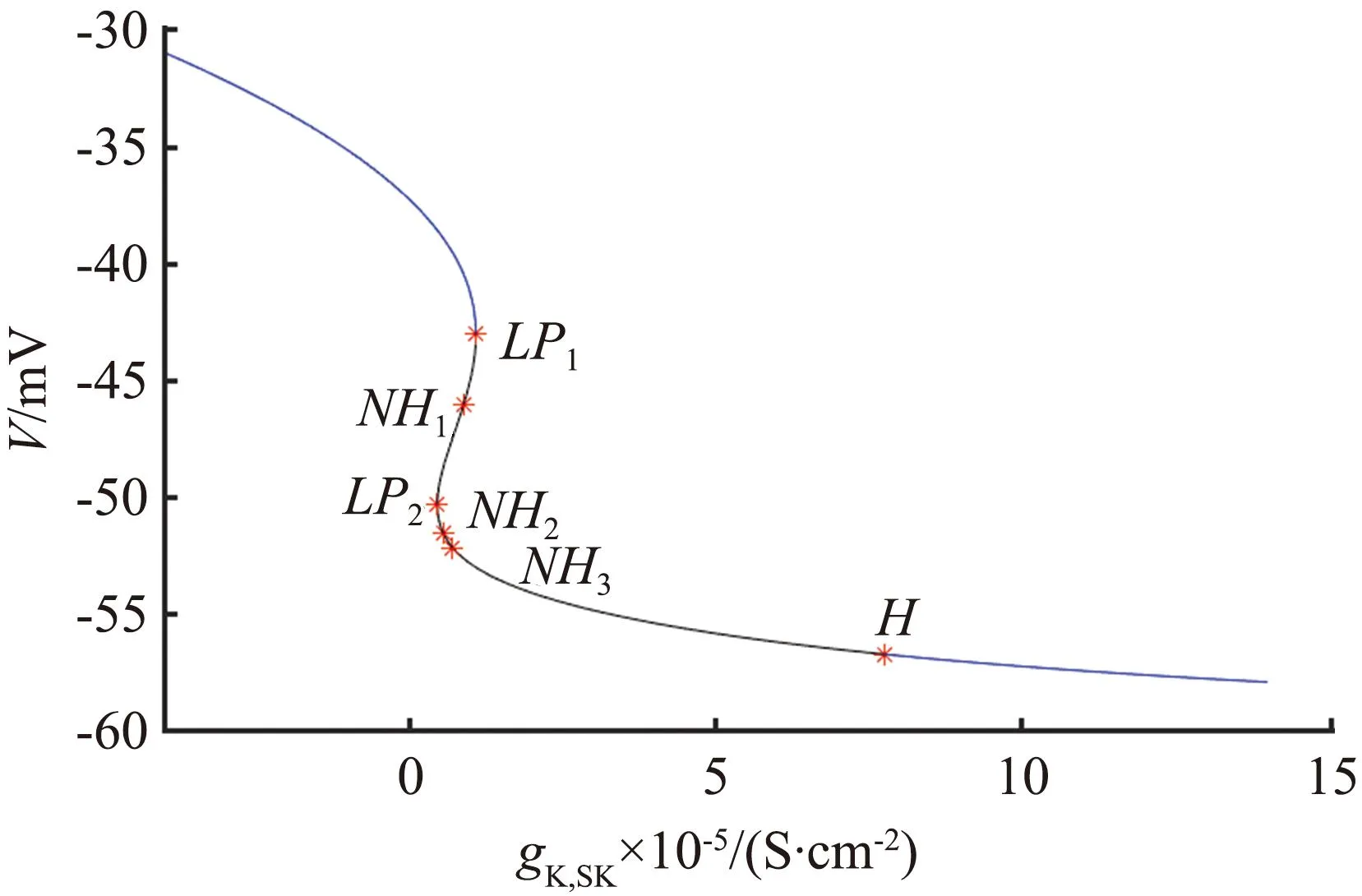
(a) gK,SK的分岔

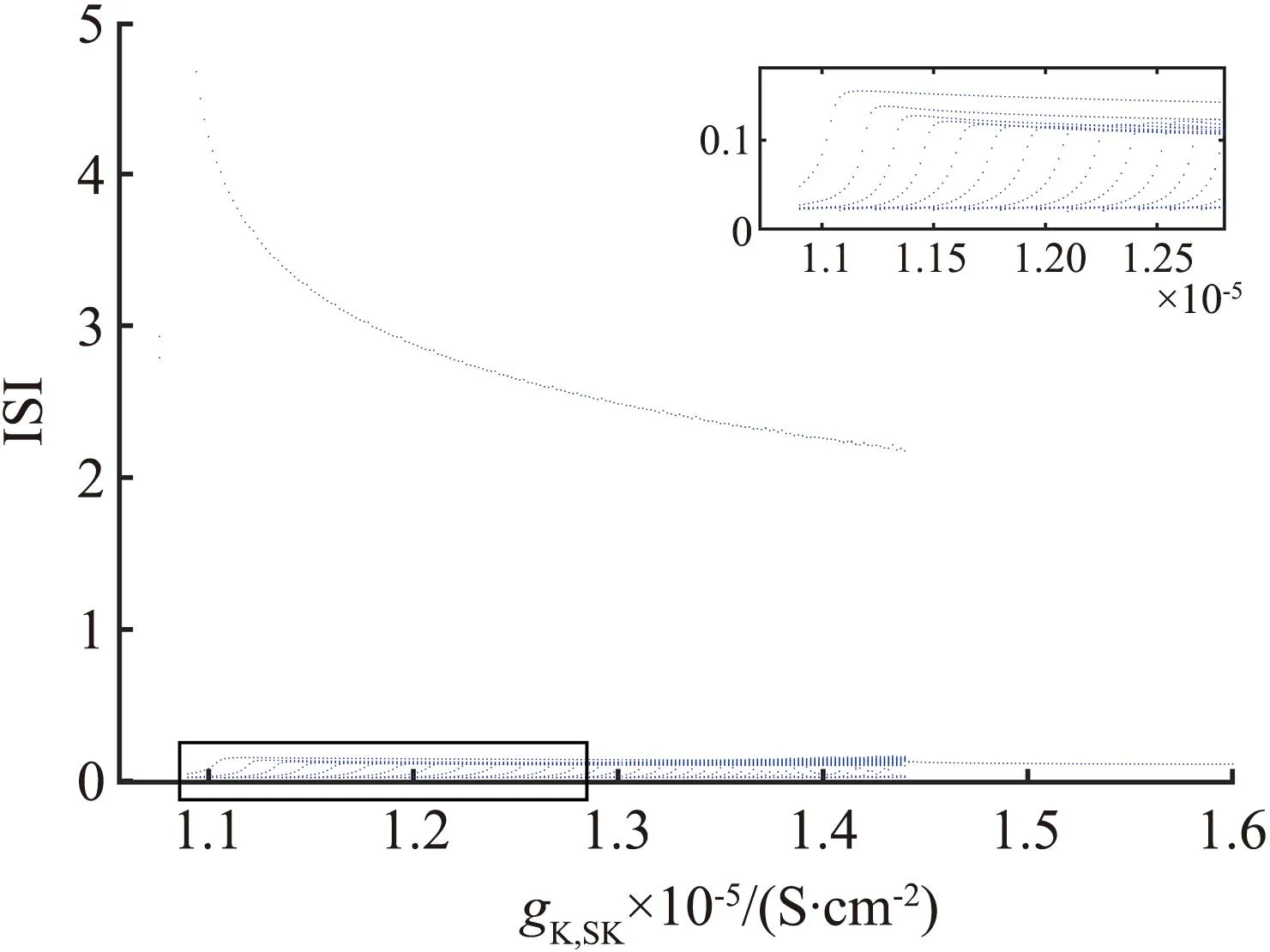
(b) gK,SK的ISI分岔

(c) Istim的分岔图3 刺激电流Istim与电导gK,SK的单参数分岔与峰峰间距(ISI)分岔比较Fig.3 Comparison of one-parameter bifurcation of stimulus current Istim and conductance gK,SK and ISI bifurcation

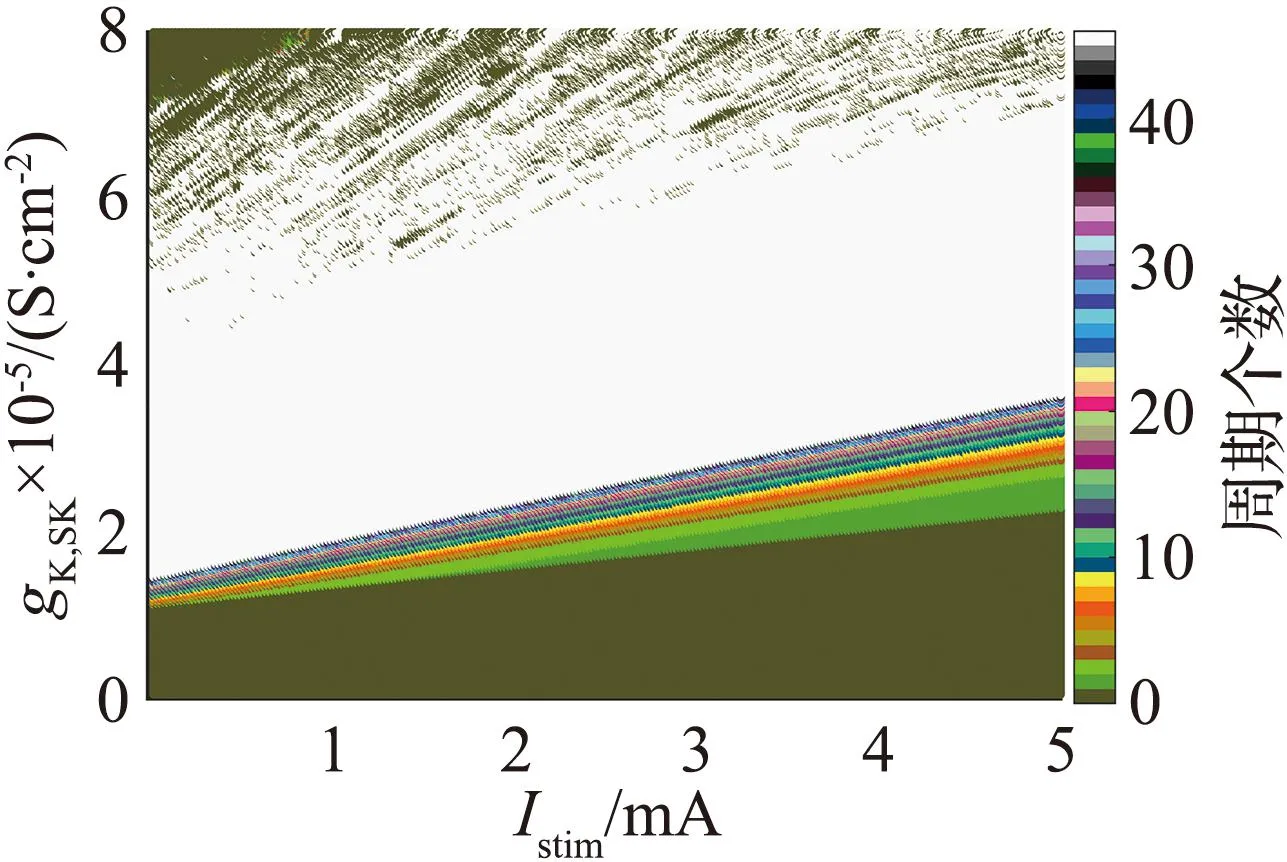
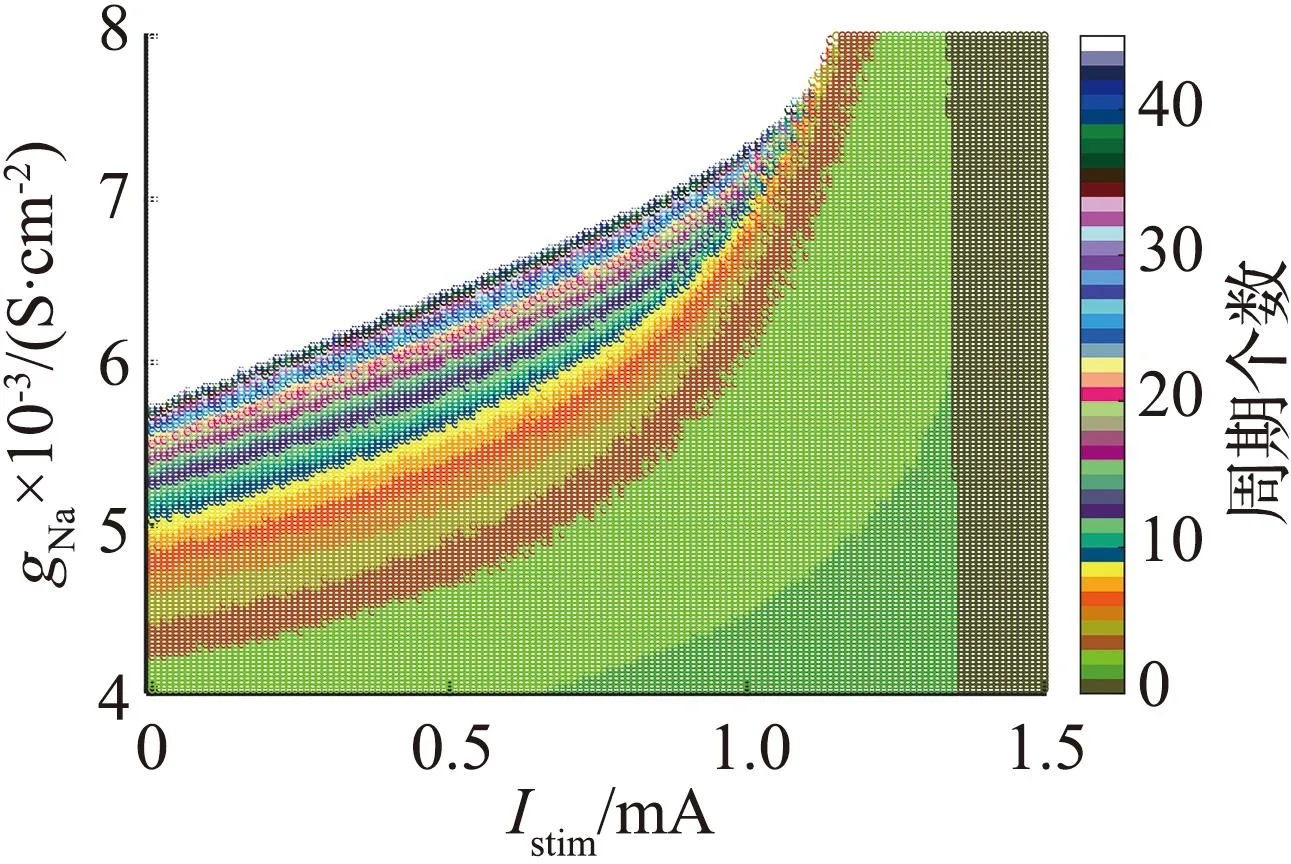
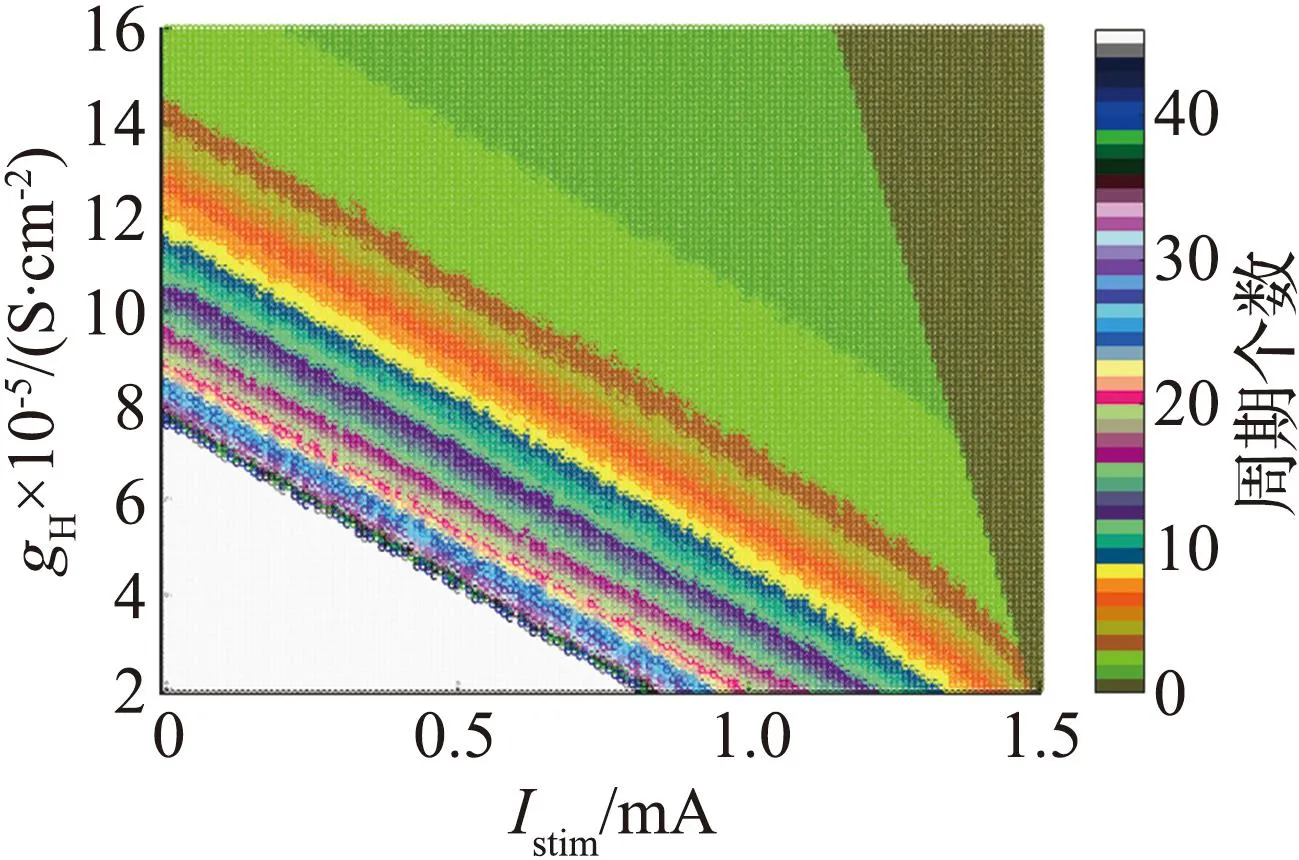
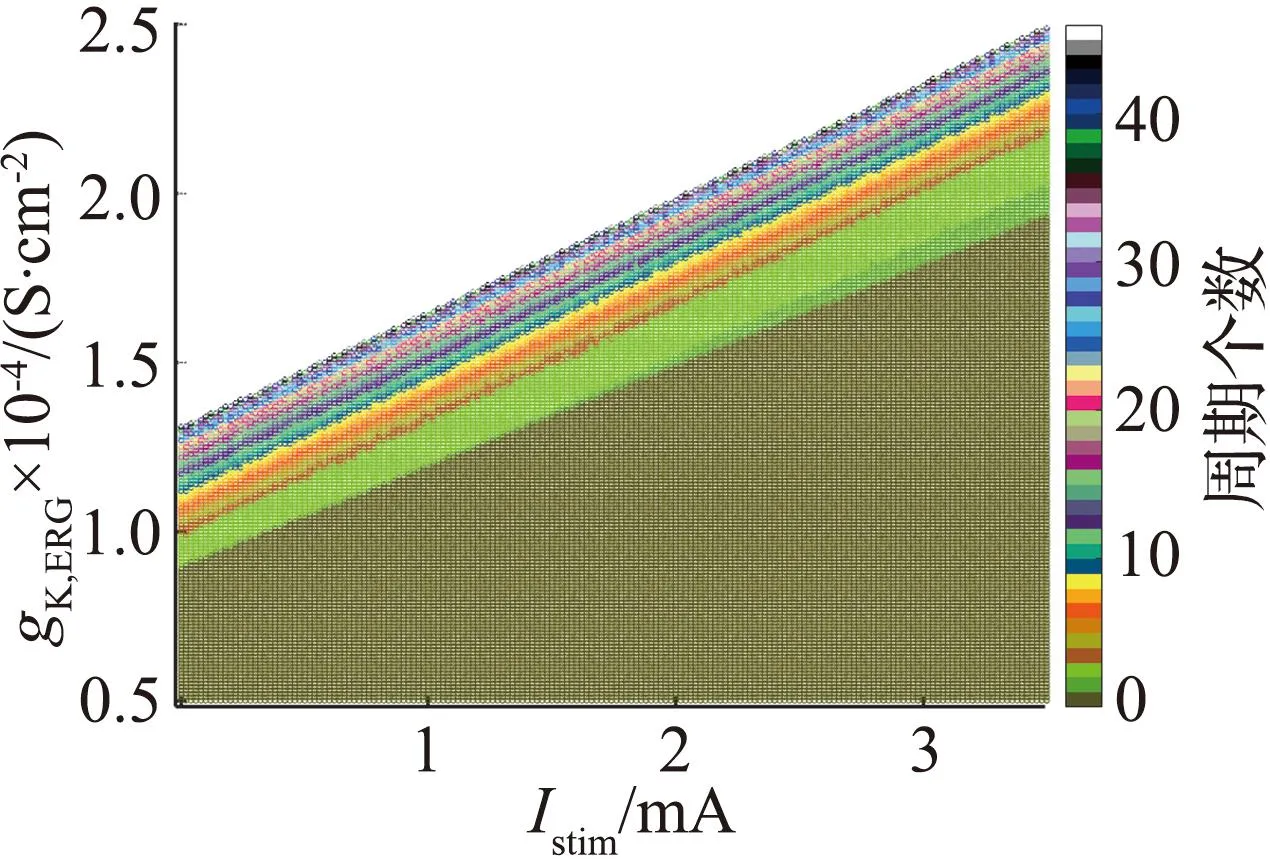
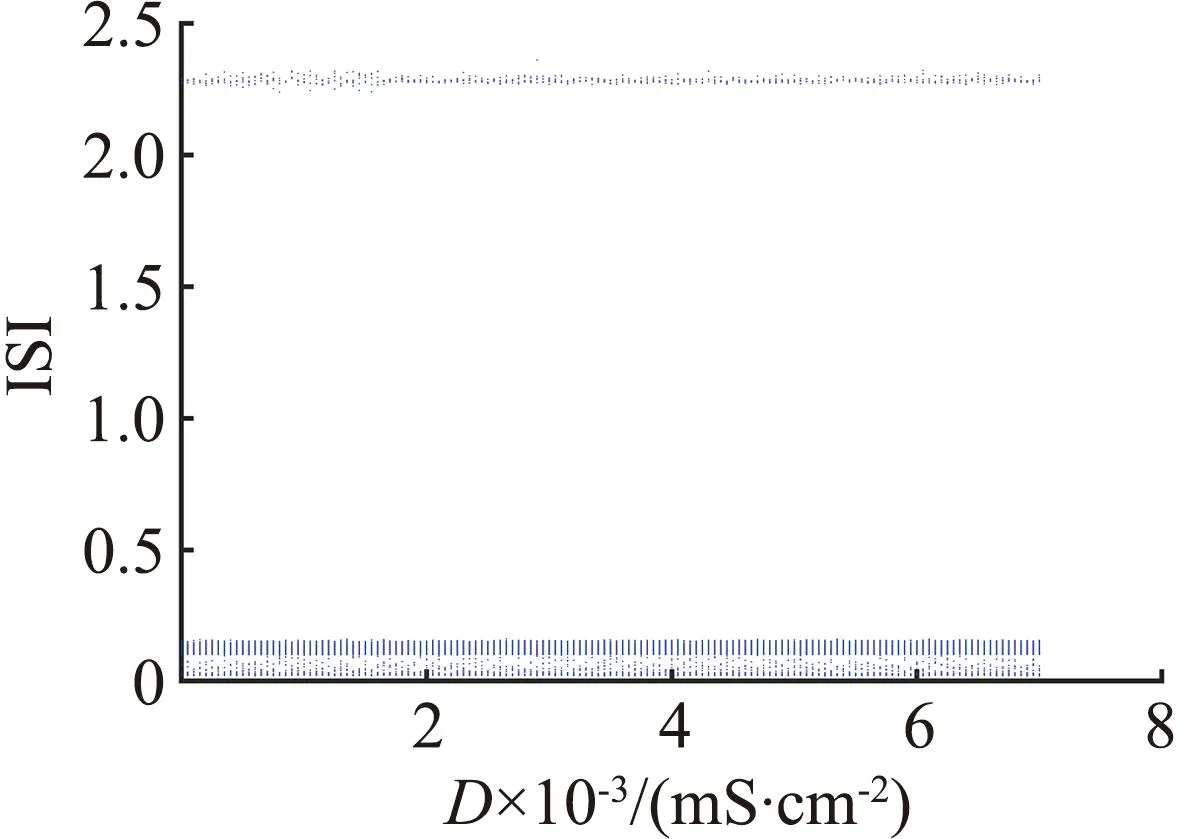
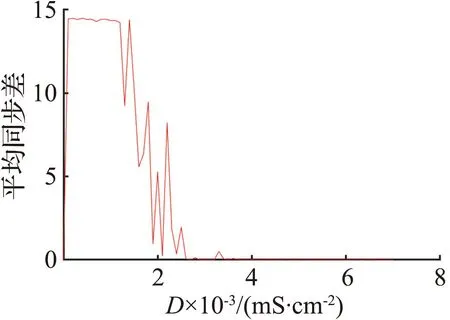
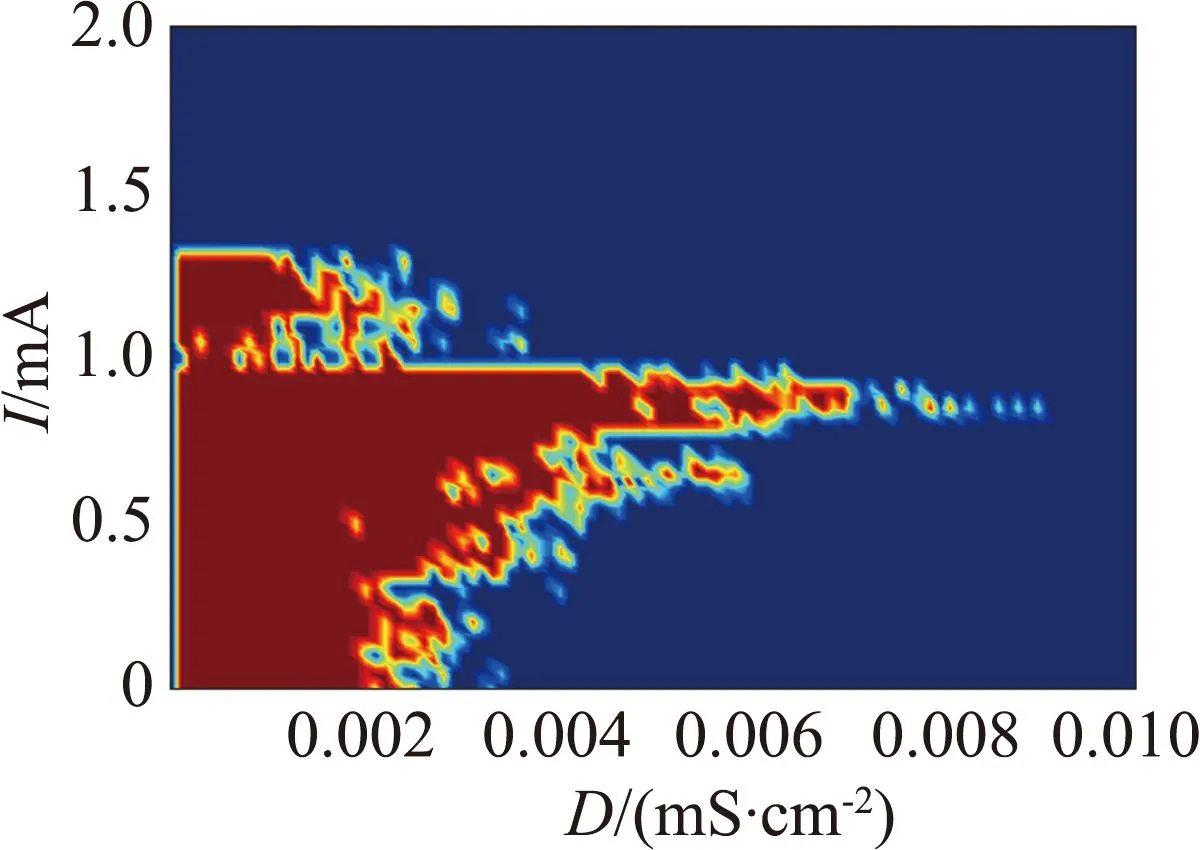
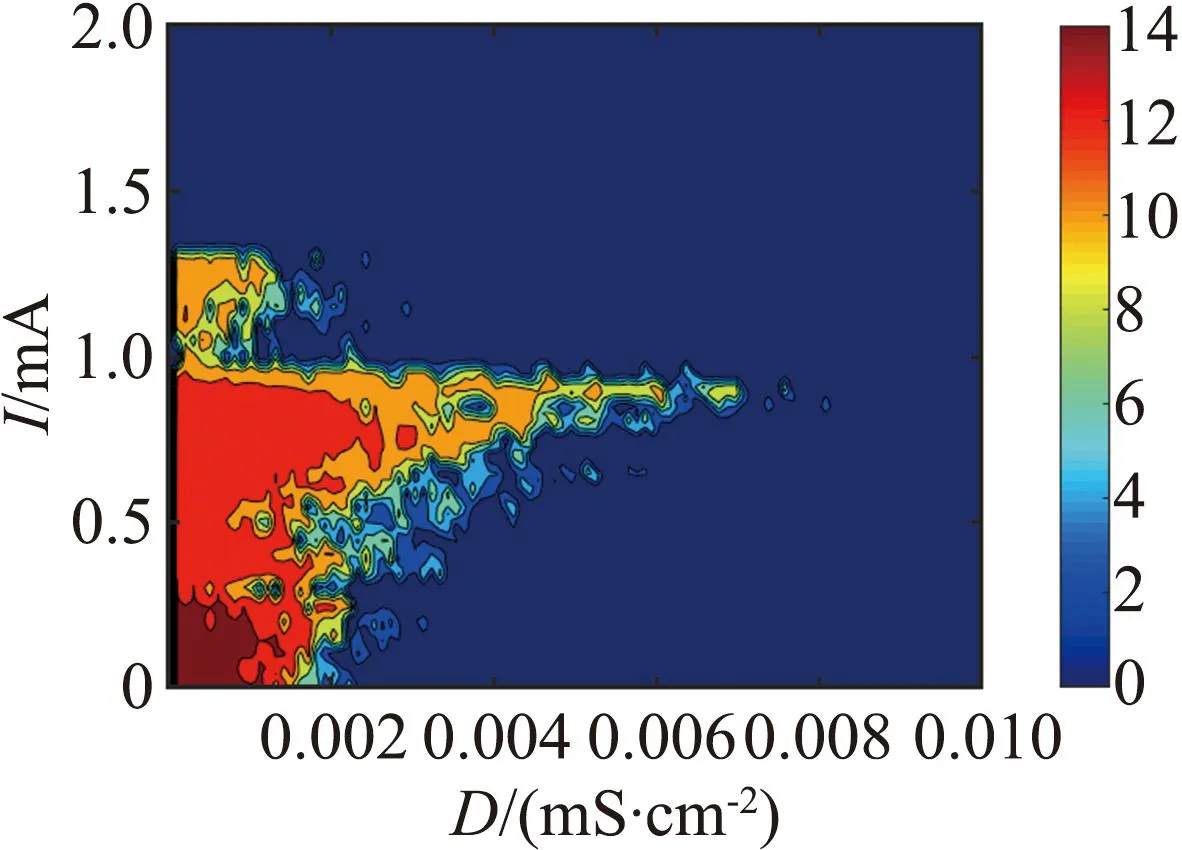
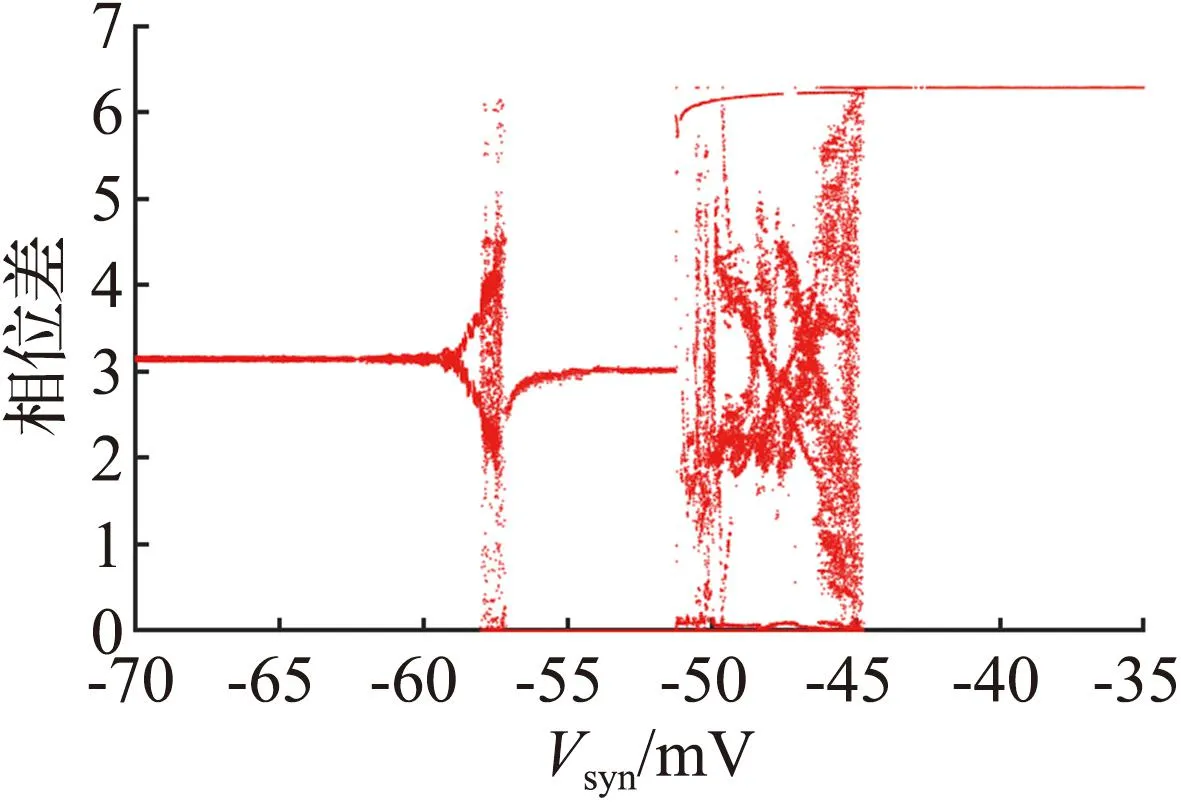
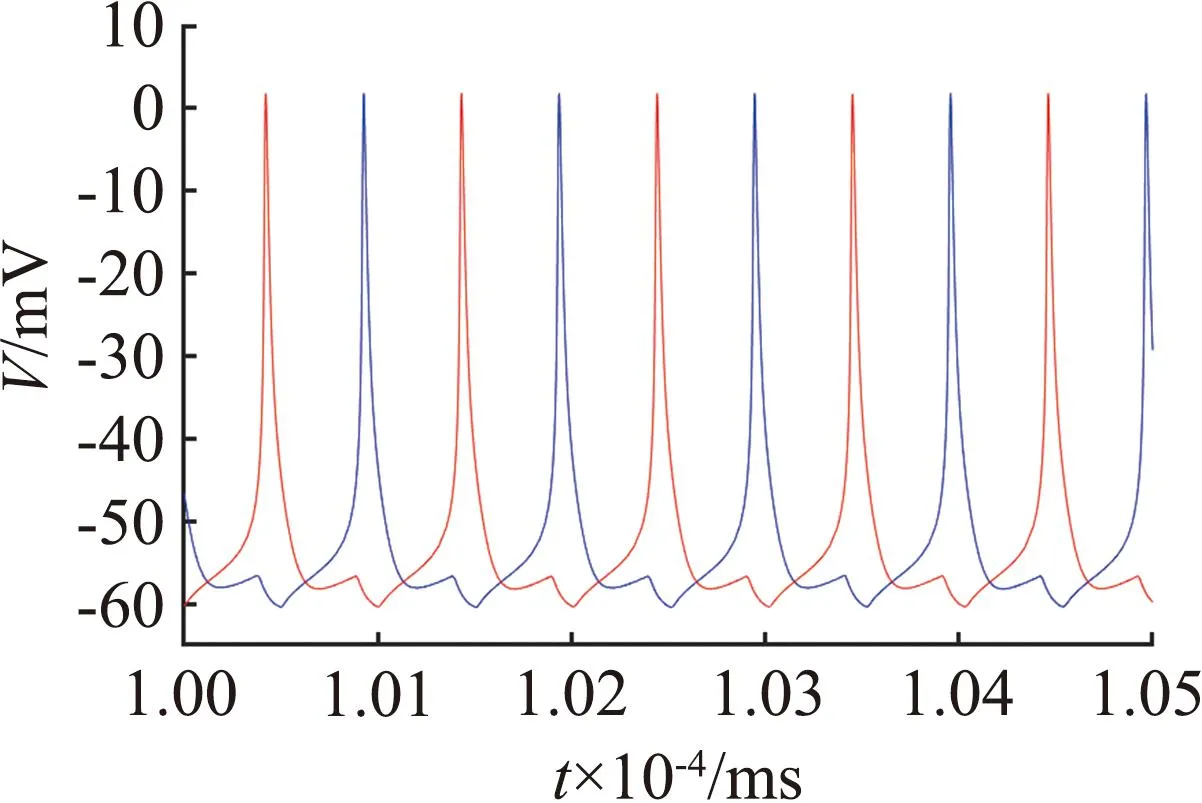
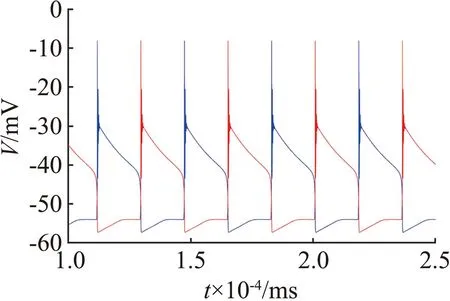
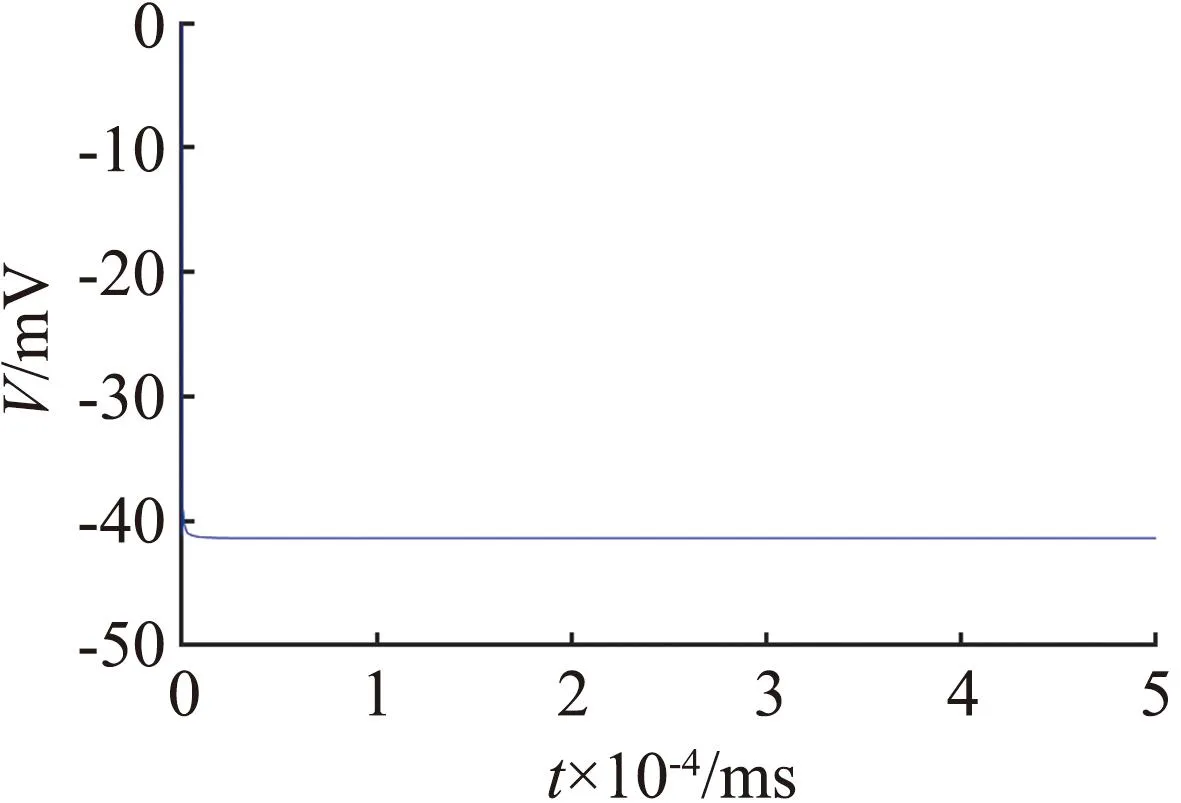
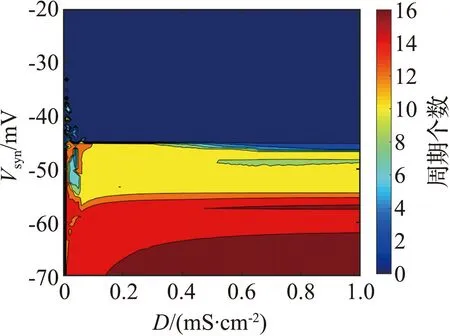
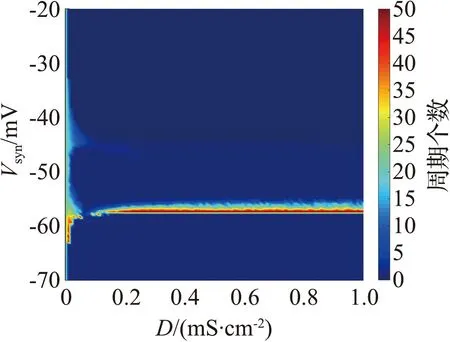
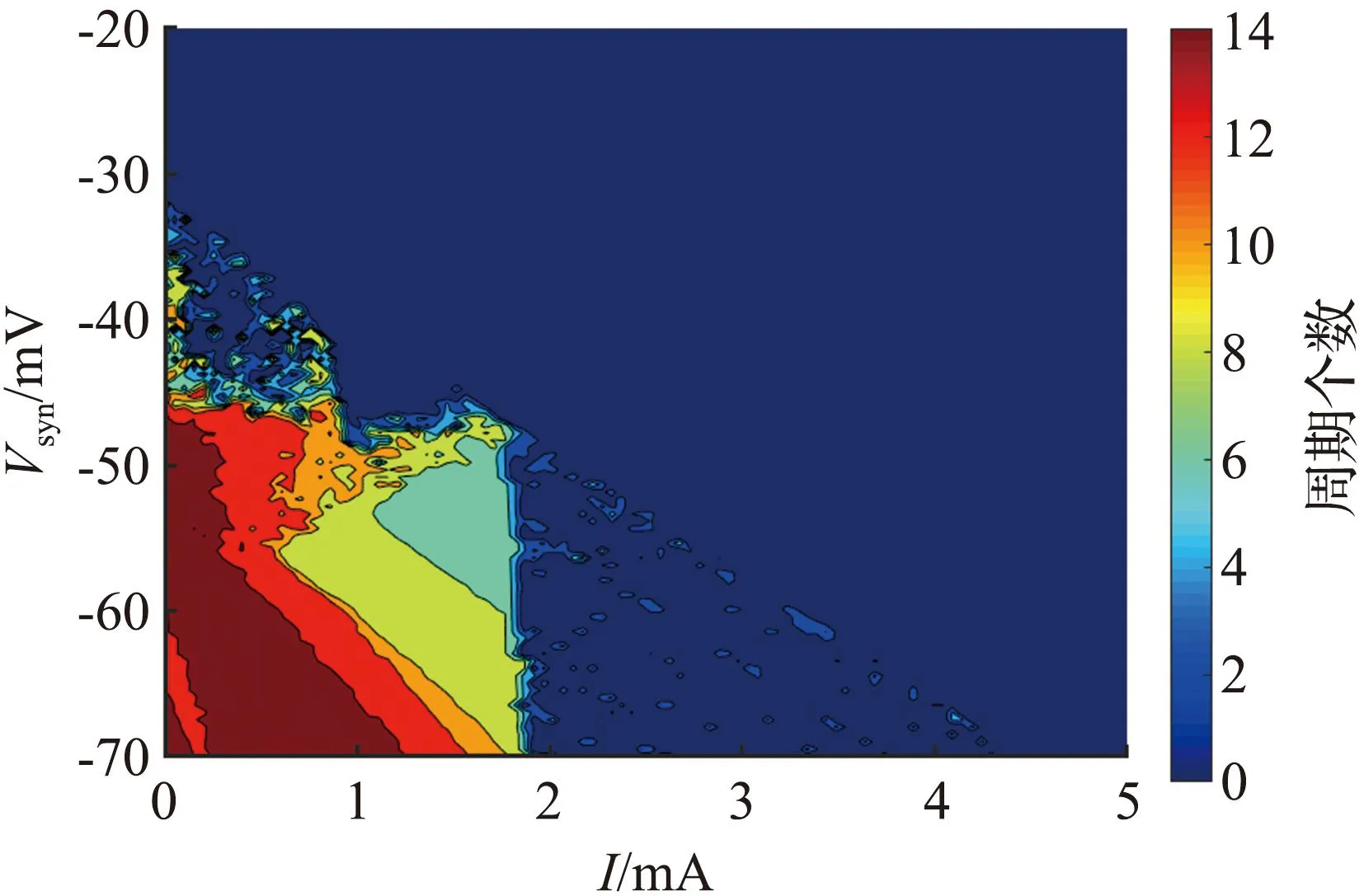
图3(a)的分岔曲线呈不明显的Z形,蓝色曲线表示稳定平衡点,黑色曲线表示不稳定平衡点。图中有一个Hopf分岔点H,以及2个鞍结分岔点LP1和LP2。随着参数gK,SK逐渐增大,神经元的静息状态经由LP1点进入放电状态,由H点回到静息状态。从图3(b)可见,gK,SK=1.09×10-5S/cm2附近进入放电状态。当1.09×10-5S/cm2

从图3(c)可见,Hopf分岔点H1、H2随着Istim逐渐增大,系统的静息状态经由H1点进入放电状态,由H2点回到静息状态。H1点是模型(4)静息和放电相互转迁的关键点,为了分析H1点的动力学性质,利用文献[18]中的方法计算H1点的第一Lyapunov系数l1(0)来确定所产生极限环的稳定性。H1点处对应的刺激电流为Istim=-0.773 78 mA,在H1点处,此时的Jacobian矩阵的特征值为λ1=-0.058 6,λ2=-0.002 0,λ3.4=±0.025 3i,存在一对实部为0的共轭特征根,从而验证了模型(4)在H1点发生了Hopf分岔。

首先,通过计算得到在H1点处的Jacobian矩阵为

式中:矩阵A|H1有一对共轭特征根λ3,4=±iω,其中ω=0.025 3,取特征值λ3对应的特征向量q,使得Aq=iωq,取AT的特征值λ4对应的特征向量p,使得ATp=-iωp,同时向量p、q满足〈p,q〉=1。经计算得到

q=(0.999 963,3.278 6×10-7-2.29×10-6i,0.004 454-0.001 743 5i,

-0.000 468 6+0.007 123 4i)T,

p=(0.545 838+0.065 7i,-3 940.79-177 179.824i,-10.174 8-5.465 6i,

-0.637 74+11.767 85i)T。

经计算得到

通过文献[17]中的计算公式可以得到第一Lyapunov系数为

因此,四维多巴胺能神经元模型(4)在H1处发生了亚临界Hopf分岔,并产生不稳定极限环。利用相同的方法,通过计算可得在H2点与H点也产生了亚临界Hopf分岔,产生不稳定极限环。

2.2 双参数分岔分析

双参数分岔图可以体现2个参数同时变化时系统性质的改变过程。模型(4)中刺激电流Istim与不同参数组合时的双参数周期分岔比较如图4所示,图中不同颜色代表不同的周期个数,对应关系展示在右侧颜色栏中,周期个数大于等于45视为混沌状态,用白色表示。

(a) Istim与gK,SK

(b) Istim与gNa

(c) Istim与gK,DR

(d) Istim与gH

(e) Istim与gL,Ca

(f) Istim与gK,ERG图4 模型(4)中刺激电流Istim与不同参数组合的双参数周期分岔比较Fig.4 Comparison of two-parameter periodic bifurcation when stimulus current Istim is combined with different parameters in model (4)

在不同参数组合下系统具有相似的分岔结构,当沿不同方向变化参数时均表现出由加周期分岔转迁至混沌态的动力学现象,且随着周期数的增大,其颜色带逐渐变窄,直至混沌状态。例如图4(b),以Istim和gNa为参数变量,当沿着平面右下至左上的方向变化参数时,系统经历了如下过程:静息态→周期1簇放电态→周期2簇放电态→周期3簇放电态→周期4簇放电态→周期5簇放电态→…→混沌放电。这种分岔结构存在于图4(a)至图4(f)中,系统通过加周期分岔与混沌区域相连接。通过不同参数组合的双参数周期分岔图,进一步了解模型反常簇发放的放电规律,为理论研究提供参考。

3 耦合模型的放电特性及同步研究

生物神经系统是许多神经元的集群,2个神经元耦合在一起构成了最小的神经元集群,与单个神经元模型相比,耦合模型表现出的动力学行为更加复杂。神经元在处理信息的过程中发生的同步行为在神经系统中广泛存在。同步行为在学习和形成记忆等方面起到至关重要的作用,并且在许多疾病背后都能看到同步现象,如癫痫、帕金森综合征等,因此,利用非线性动力学理论探究神经元的同步放电活动,能够给医学研究提供一定的理论启发。下面构建2个简化多巴胺能神经元的电突触耦合模型和化学突触耦合模型,分别探究模型参数对2个神经元耦合模型放电特性的影响和同步状态转迁过程,得到耦合模型实现同步的条件。

3.1 同步特征指标

引入神经元膜电位的相位差[19]和平均同步差度量2个耦合神经元的同步性。记录2个神经元到达动作电位峰值的时刻,那么2个耦合神经元的相位差可以定义为

式中tn、ts分别为2个耦合神经元到达峰值的时间。当Δφ=0或2π时,耦合模型为相位同步状态;当Δφ取值为固定数,且不完全为0或2π时,耦合模型为反相同步状态;当Δφ为[0,2π]中的任意值时,耦合模型为异步状态。由于相位差指标不足以区分本文后续会出现的静息异步状态和相位同步状态,因此下面引入平均同步差指标作为补充。

假设耦合模型中2个神经元的微分方程组得到的解分别为(x1,y1,z1,w1)与(x2,y2,z2,w2),那么耦合模型的平均同步差e的计算公式为

3.2 电突触耦合模型的放电特性及同步研究

3.2.1 电突触耦合模型

电突触耦合模型如下:

(5)

式中:i,j∈{1,2},且i≠j;Vi表示第i个神经元的膜电位;Ii表示第i个神经元受到的外界刺激电流;D表示2个神经元之间的耦合连接强度,该耦合模型中所有参数值与模型(4)相同。

3.2.2 刺激电流对电突触耦合模型的影响

刺激电流的ISI分岔图与同步指标比较如图5所示。对电突触耦合模型(5)添加刺激电流I1=I2=I,通过峰峰间距分岔图、相位差及平均同步差观察I变化对电突触耦合模型(5)同步的影响,这里耦合强度D=0.001 mS/cm2。

(a) 刺激电流的ISI分岔

(b) 相位差

(c) 平均同步差图5 刺激电流的ISI分岔图与同步指标比较Fig.5 Comparison of ISI bifurcation diagram and synchronization index of stimulus current

当I∈[0,1.35]时,神经元表现簇放电态,模型相位差值混乱,耦合模型处于异步状态。当I>1.35 mA时,神经元由簇放电转迁至静息,模型相位差值为2π,同步差值为0,耦合模型达到完全静息同步状态,因此在电突触耦合模型(5)中,改变刺激电流可以诱导耦合系统达到完全静息同步。

3.2.3 耦合强度对电耦合系统的影响

耦合强度影响了系统的同步性,但对神经元放电模式并无影响。耦合强度D的ISI分岔图与同步指标比较如图6所示,其中刺激电流I1=I2=0。

(a) 耦合强度的ISI分岔

(b) 相位差

(c) 平均同步差图6 耦合强度D的ISI分岔图与同步指标比较Fig.6 Comparison of ISI bifurcation diagram of coupling strength D and synchronization index

从图6可见,耦合强度D变化时神经元始终表现为规律的簇放电态。当0

3.2.4 电突触耦合模型在双参数平面的同步

利用二维平面的同步状态、平均同步差、动作电位周期个数分布探究(D,I)参数平面上的同步行为。(D,I)参数平面上同步指标与周期个数比较如图7所示。其中图7(a)中红色代表异步,绿色代表反相同步,蓝色代表相位同步。

(a) 同步状态

(b) 平均同步差

(c) 周期个数图7 (D,I)参数平面上同步指标与周期个数比较Fig.7 Comparison of synchronization index and the number of period in (D,I) parameter plane

观察图7可知,较小的D和I不利于耦合模型达到同步,由异步转迁到相位同步的过程中会经历短暂的反相同步状态。随着D和I同时增大,平均同步差的值逐渐减小,耦合模型趋于同步状态。从图7(c)可见,随着I的增大,簇放电周期个数不断减少,而D对周期个数几乎没有影响,进一步验证了前面的结论。当I>1.35 mA时,神经元为静息态,该电突触耦合模型在达到完全同步时神经元有2种发放模式,分别是周期簇发放和静息态。

对于电突触耦合模型(5),其放电模式受刺激电流影响较大,系统的同步状态则受到刺激电流和耦合强度的共同影响,当I<1.35 mA时,改变耦合强度可以诱导耦合系统达到簇同步状态;当I>1.35 mA时,改变耦合强度可以诱导耦合系统达到静息同步状态。

3.3 化学突触耦合模型的放电特性及同步研究

3.3.1 化学突触耦合模型

化学突触耦合模型如下:

(6)

式中:i,j∈{1,2},且i≠j;Vsyn为突触的逆转电位,其取值决定化学耦合是抑制还是兴奋;θ为突触阈值;σ为兴奋或抑制开始的比率常数;其他参数与模型(4)相同。

3.3.2 刺激电流对化学突触耦合模型的影响

模型(6)中刺激电流的ISI分岔图与同步指标比较如图8所示。对化学突触耦合模型(6)施加外界刺激I1=I2=I,观察神经元发放模式的改变和耦合系统的同步情况,其中σ=10,θ=-45,D=0.010 mS/cm2,Vsyn=-60 mV。

(a) I=0 mA

(b) I=0.7 mA

(c) I=2.2 mA

(d) ISI分岔

(e) 相位差

(f) 平均同步差图8 模型(6)中刺激电流的ISI分岔图与同步指标比较Fig.8 Comparison of ISI bifurcation diagram of stimulus current and synchronization index in model (6)

改变化学突触耦合模型中刺激电流的取值使神经元表现出一种特殊的混合模式振荡现象,如图8(b)至图8(c)所示。该混合模式振荡由大幅振荡和小幅振荡组成,大幅振荡表现为周期簇放电,保持了单神经元模型所具有的以去极化阻断结尾的反常簇形态,小幅振荡表现为相邻簇间的多个凸起结构。如图8(d)所示,随着电流的增大,在混合模式振荡过程中存在逆加周期分岔的动力学现象,大幅振荡的簇内峰数目和小幅振荡的凸起数量都在逐渐减少。随着刺激电流的增大,耦合神经元的放电活动经历峰放电→混沌状态→混合模式振荡的转变过程。当I>3.2 mA时,神经元为静息态,对应相位差值为2π,平均同步差值为0,耦合模型达到静息同步状态。

综上,在化学突触耦合模型中,改变刺激电流不仅使得神经元表现出混合模式振荡的复杂现象,还可以诱导耦合系统达到静息同步状态。

3.3.3 突触逆转电位对化学突触耦合模型的影响

模型(6)中突触逆转电位的ISI分岔图与同步指标比较如图9所示。讨论突触逆转电位Vsyn变化时,耦合神经元放电模式的变化以及化学耦合模型(6)的同步状态转迁过程,其中σ=10,θ=-45,D=0.100 mS/cm2,I1=I2=0.1 mA。

(a) ISI分岔

(b) 相位差

(c) 平均同步差

(d) Vsyn=-65 mV

(e) Vsyn=-55 mV

(f) Vsyn=-40 mV图9 模型(6)中突触逆转电位的ISI分岔图与同步指标比较Fig.9 Comparison of ISI bifurcationdiagram of synaptic reversal potentialand synchronization index in model(6)

随着突触逆转电位增大,耦合模型同步状态的转迁过程为反相同步→异步→反相同步→异步→簇同步→静息同步。几个同步状态分别为:当Vsyn<-58 mV时,耦合神经元处于反相同步的峰放电状态,图9(d)为Vsyn=-65 mV时耦合神经元的放电序列图,蓝线和红线分别表示耦合模型第1、2个神经元的放电序列;当-57 mV-43 mV时,耦合模型达到静息同步状态,如图9(f)所示。综上,当突触逆转电位Vsyn取合适值时,能使得化学耦合模型(6)达到簇同步状态或静息同步状态。

3.3.4 化学突触耦合模型在双参数平面的同步

刺激电流I与突触逆转电位Vsyn都能够影响化学耦合模型的同步状态,下面研究这2个参数与耦合强度D如何共同影响模型(6)的同步状态。当Vsyn=-60 mV时,模型(6)的同步状态、平均同步差、动作电位周期个数在(D,I)参数平面的分布如图10所示。在图10(a)中,蓝色代表相位同步,绿色代表反相同步,红色代表异步。(D,I)参数平面左下方存在一个类三角反相同步区域。

(a) 同步状态

(b) 平均同步差

(c)周期分布图10 当Vsyn=-60 mV时,模型(6)的同步状态、平均同步差、动作电位周期个数在(D,I)参数平面的分布Fig.10 Distribution of the synchronization, mean synchronization difference and the number of action potential period in the parameter plane (D,I) When Vsyn=-60 mV in model (6)

当I∈[0.3,1.4]时,增大D使得耦合系统经历异步→反相同步→异步的转迁过程。

当I∈(1.4,1.9]、D>0.05 mS/cm2时,耦合系统处于相位同步状态。但图10(b)中对应的平均同步差却不为0,结合图10(c)可知,这是由于2个耦合神经元都处于静息状态,但所处静息电位不相同,称这种状态为静息异步;当I>1.9 mA时,在弱耦合区域存在异步状态,当D大于某个阈值时,耦合系统达到静息同步。

图10(c)中不同灰度代表不同周期个数,周期个数大于50视为混沌态,存在一条红色混沌带,混沌带下方为单峰放电,上方为周期簇放电,且随着I增大,周期个数逐渐减少,直至静息。综上所述,较小的刺激电流不利于化学耦合模型达到同步状态,只有刺激电流处于一定范围内,才能使得耦合系统达到完全同步状态。

当I=0.1 mA时,模型(6)的同步状态、平均同步差、动作电位周期个数在(D,Vsyn)参数平面的分布如图11所示。

在图11(a)中,蓝色代表相位同步,绿色代表反相同步,红色代表异步。(D,Vsyn)参数平面存在一个长条形反相同步区域。当-58 mV-45 mV时,在弱耦合区域同样存在异步状态,D大于某阈值后耦合模型达到静息同步。从图11(b)可见,只有参数Vsyn处于一定范围内时,耦合模型才能达到完全同步状态。从图11(c)可见,当Vsyn≈-57 mV时,存在一条红色混沌带。经过分析得到,在这条混沌带下方,神经元为单峰放电,混沌带上方为周期簇放电;当Vsyn>-45 mV时,耦合神经元达到静息状态。由此可知,图11(a)中反相同步区域大多对应周期簇放电,其下方的异步区域为单峰放电,上方的相位同步区域对应静息状态。

(a) 同步状态

(b) 平均同步差

(c) 周期分布图11 当I=0.1 mA时,模型(6)的同步状态、平均同步差、动作电位周期个数在(D,Vsyn)参数平面的分布Fig.11 Distribution of the synchronization, mean synchronization difference and the number of action potential period in the parameter plane (D,Vsyn) When I=0.1 mA in model (6)

由上述分析可知,只有适当范围内的刺激电流I和突触逆转电位Vsyn能够使得化学耦合系统(6)达到完全同步状态。

利用不同耦合强度D的(I,Vsyn)双参数平面内平均同步差变化反映耦合强度D在I和Vsyn为参数情况下模型的同步情况。

耦合强度D分别为0.001、0.005、0.010、0.100 mS/cm2时,模型(6)在(I,Vsyn)平面的平均同步差变化情况如图12所示。不同颜色代表平均同步差的不同值,蓝色代表完全同步状态。可以发现,随着耦合强度D的增大,非同步区域逐渐向(I,Vsyn)平面左下角靠拢,形成一个规则的方形非同步区域。

(a) D=0.001 mS/cm2

(b) D=0.005 mS/cm2

(c) D=0.010 mS/cm2

(d) D=0.100 mS/cm2图12 不同耦合强度下,模型(6)在(I,Vsyn)平面的平均同步差变化情况Fig.12 Variation of mean synchronization difference in (I,Vsyn) plane of model (6), under different coupling strength

当I和Vsyn的值沿着45°方向增大时,平均同步差呈现逐渐减小到0的趋势,表明对于化学耦合多巴胺能神经元模型(6)而言,完全同步状态不仅依赖于耦合强度,还依赖于刺激电流和突触逆转电位的取值。在合适的耦合强度下,较强的刺激电流或较大的突触逆转电位可以诱导化学耦合模型出现完全同步状态。

4 结论

本文通过分岔理论研究简化多巴胺能神经元模型的动力学性质,发现SK通道电导的增加使得模型出现加周期分岔的动力学现象,并发现在不同参数组合下,沿着二维参数平面的不同方向,模型均呈现出由加周期分岔转迁至混沌状态的动力学现象。通过分岔分析增进了对模型不同参数变化介导去极化型反常簇行为这一现象的了解,能够为医学生理实验提供一定的理论基础。许多疾病的发生与神经模型异常同步有关,本文构建了2个神经元电突触与化学突触耦合模型,研究模型参数对耦合神经元放电模式的影响以及耦合模型同步转迁规律,得到耦合模型达到完全同步的条件。对于电耦合模型,在刺激电流小于1.35 mA时,可以通过改变耦合强度诱导模型达到簇同步状态;在刺激电流大于1.35 mA时,可以通过改变耦合强度诱导模型达到静息同步状态。对于化学耦合模型,随着耦合强度的增大,在刺激电流和突触逆转电位的参数平面左下角逐渐形成规则的方形非同步区域。在合适的耦合强度下,较强的刺激电流或较大的突触逆转电位可以诱导化学耦合模型达到完全同步状态。本文耦合模型的同步状态不仅受耦合强度的影响,还受到外界刺激电流以及模型参数的影响。本文的研究结论为研究神经元模型的动力学性质和耦合模型的同步性提供参考,关于多个神经元耦合的网络模型的同步是值得进一步研究的内容。