分数阶移相全桥变换器的建模与优化控制

陈新帅, 刘玉芝*, 杨鹏, 李倩

(1.石家庄铁道大学 河北省交通电力网智能融合技术与装备协同创新中心, 河北 石家庄 050043;2.石家庄铁道大学 电气与电子工程学院, 河北 石家庄 050043;3.国网河北省电力公司科技部, 河北 石家庄 050000)

0 引言

随着电动汽车充电、光伏电站和通信基站等领域电力需求的不断增加,能源转换技术迎来了新的挑战与机遇。移相全桥变换器作为一种重要的能量转换电路,得到了广泛的应用。在满足不断增长的电力需求方面,基于第三代半导体材料的客户侧感知设备电源电路模块研制成为当今的热点领域。第三代半导体材料,如碳化硅(SiC)和氮化镓(GaN),具有更高的电子迁移率和能带宽度,使得它们在大功率、高频率和高温环境下表现出色[1]。人们采用第三代半导体材料设计出的电源电路模块能够实现更高的效率、更小的尺寸以及更可靠的性能,以满足不断增长的能源转换需求。在全桥DC-DC变换器中,软开关技术(zero voltage switching, ZVS)的实现可以提高全桥DC-DC变换器的性能。一方面,可以对变换器的可靠工作提供保证,另一方面,可以降低开关损耗和电磁干扰(electro magnetic interference, EMI)[2]。

近年来,分数阶微积分理论的快速发展引起了电气工程领域的广泛关注。分数阶微积分理论能够更准确地描述和解释电气系统中的复杂行为,并为其优化和控制提供了新的方法和工具。通过引入分数阶元件,可以在电路设计中获得更大的自由度和灵活性[3-4],此外,一些电气元件的常规模型因其自身的局限性,可能被非整数阶模型所替换。现有研究表明,实际生活中并不存在整数阶电容和电感,通过分数阶理论对实际电感、电容进行建模和仿真,证明了实际电感、电容的阶次为非整数。

开关变换器的建模是分析和设计控制器的基础。研究表明,与传统的整数阶控制器相比,分数阶控制器具有明显的优势,在其控制下的分数阶电路仿真模型具有更优的动态性能和鲁棒性[5]。文献[6]中基于Buck变换器的小信号模型,建立了移相全桥变换器的小信号模型及考虑占空比丢失情况下的小信号模型,但未考虑电容和电感元件为分数阶的特性。文献[7]中根据电路平均基本建模法对移相全桥变换器进行小信号建模,并基于电感电流平均值方程进一步建立了峰值电流控制下移相全桥变换器的精确模型,但也忽略了电容和电感元件的分数阶特性。相较于传统的整数阶比例-积分-微分(proportion integration differentiation, PID)控制器,分数阶控制器引入了分数阶微积分理论的概念,最早由Podlubny教授提出[8],允许控制器的阶次为非整数,这种灵活性使得分数阶控制器能够更好地适应非线性系统的复杂性,并处理一些传统PID控制器难以应对的问题,实现更优的动态性能和鲁棒性。文献[9]中基于Boost变换器的等效电路模型,进行分数阶控制器的设计,对Boost电路的动态特性和稳定性进行了研究。文献[10]中基于移相全桥变换器的小信号模型,利用遗传算法对分数阶控制器参数进行了整定,对移相全桥变换器的动态性能进行了研究。目前,对于基于移相全桥变换器的分数阶模型及其控制策略的研究相对较少。

本文中以分数阶移相全桥变换器为控制对象,首先,采用状态空间平均法建立分数阶移相全桥变换器的状态空间平均模型;其次,利用分数阶微积分算法,得到电感和电容的等效分数阶模型,通过研究分数阶特性对系统频域响应的影响,深入了解系统的动态性能和稳定性,为优化控制策略和提高系统效率提供支撑;最后,设计基于遗传算法的分数阶控制器,用于控制分数阶系统,为进一步优化控制性能,采用遗传算法结合误差绝对值积分准则(integral of timed absoluted error, ITAE)来确定分数阶控制器的最优控制参数,以实现系统的最优控制性能。

1 移相全桥变换器分数阶建模

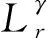
图1 分数阶移相全桥变换器电路Fig.1 Circuit diagram of fractional-order phase-shifted full-bridge converter

移相全桥变换器的工作波形如图2所示,其中每只MOS管的控制时序相互独立,这些控制时序可以分为10个开关模态。通过合理设置死区时间,使得控制波形的占空比略小于50%。其中开关管Q3和Q4的控制信号相对于开关管Q1和Q2的控制信号移相,以允许进行ZVS转换,ILr、VH和VL分别表示变压器一次侧的电流、电压和变压器二次侧的电压。

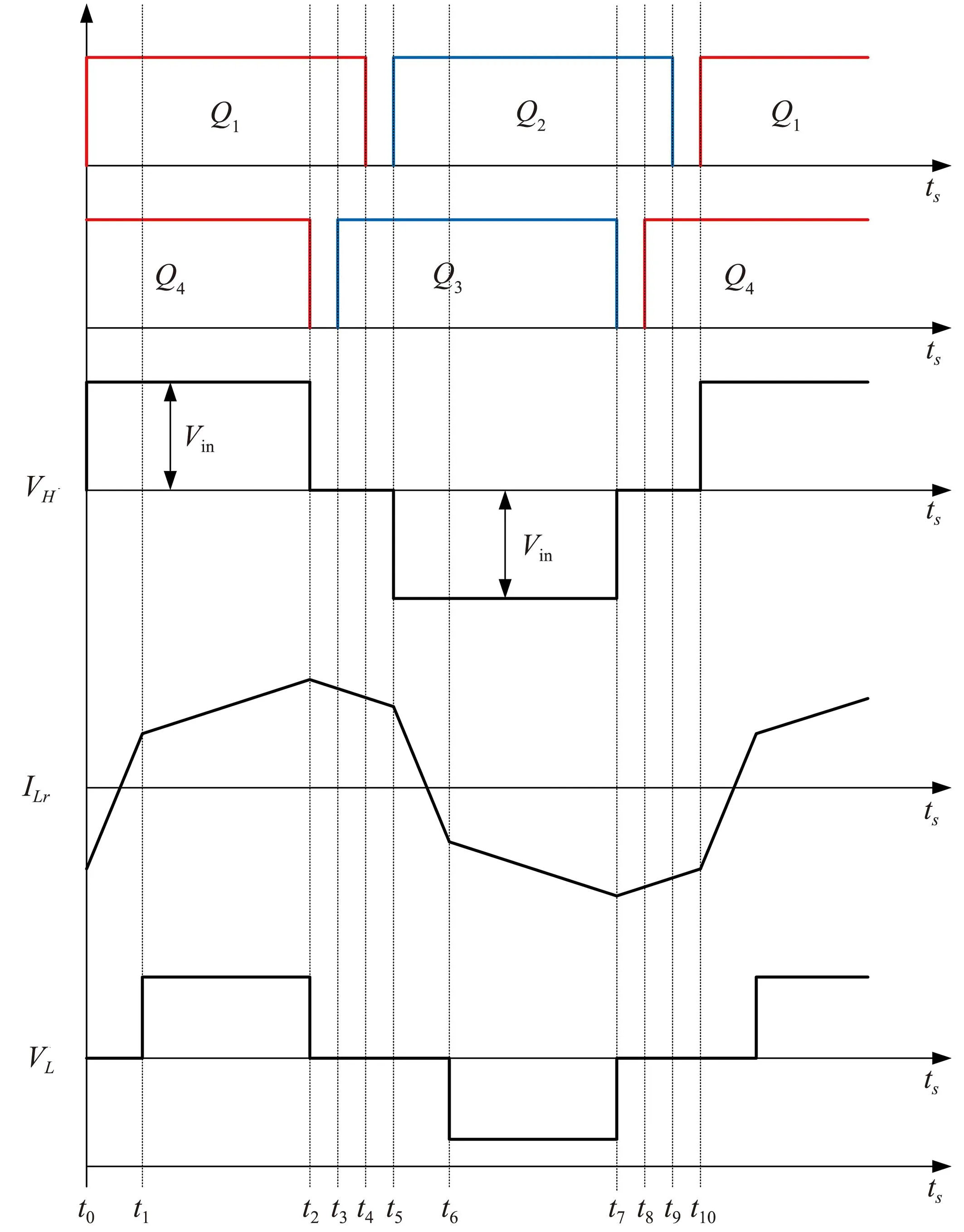
图2 移相全桥变换器的工作波形Fig.2 Working waveform of phase-shifted full-bridge converter

由于谐振电感电流在整个开关周期Ts内具有对称特性,因此可以仅考虑谐振电感电流在半周期T内的变化情况。电感电流波形如图3所示。

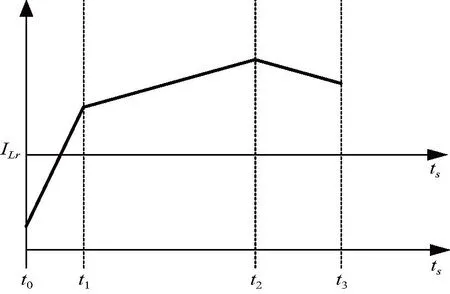
图3 电感电流波形Fig.3 Inductance current waveform

分数阶电感和分数阶电容两端电压与流过电流关系[11]分别如式(1)、(2)所示。

(1)

(2)

式中:α、β分别为电感和电容的阶次,且0<α<1,0<β<1;vL、vC分别为分数阶电感和分数阶电容两端的电压;iL、iC分别为流经分数阶电感和分数阶电容的电流;L、C分别为电感和电容。

对式(1)、(2)进行分数阶Laplace变换可得

VL(s)=LsαiL(s),

(3)

iC(s)=CsβVC(s)。

(4)

假设占空比为d,功率开关管通、断过程下的分数阶移相全桥变换器的分数阶数学模型如下:

工作模态1:Q1、Q4导通,输入电压为+Vin。

(5)

式中:α、β、γ分别为滤波电感、滤波电容和谐振电感的阶次;Vg为输入电压、V0为分数阶电容两端的电压、V1为分数阶谐振电感两端的电压、iL为流经分数阶滤波电感的电流、iL1为流经分数阶谐振电感的电流;L为滤波电感值;C为滤波电容值;L1为Lr从变压器T原边经过等效变换到副边所对应的谐振电感值;R为负载电阻。

工作模态2:Q1、Q3导通,输入电压为0。

(6)

工作模态3:输入电压反向,大小不变,状态方程同工作模态1。

工作模态4:输入电压为0,状态方程同工作模态2。

分数阶移相全桥变换器的工作状态随着功率开关管的通断而在不同的工作状态之间转换,占空比d反映了功率开关管在一个周期T内的通断时间,可以通过调节d来控制变换器。

对于开关频率足够高的移相全桥变换器,在一个开关周期内可以近似地假设所有相关变量保持不变。根据开关周期状态平均法,在一个开关周期内求平均值。

(7)

引用平均算子

(8)

对式(8)推导

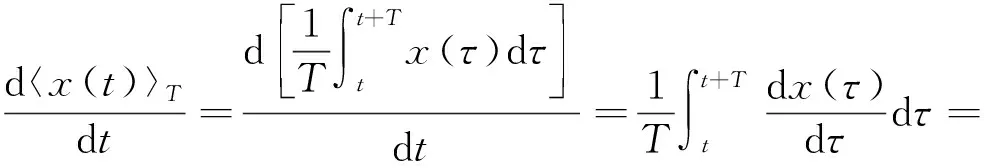
(9)

移相全桥变换器的分数阶状态平均模型可表示为

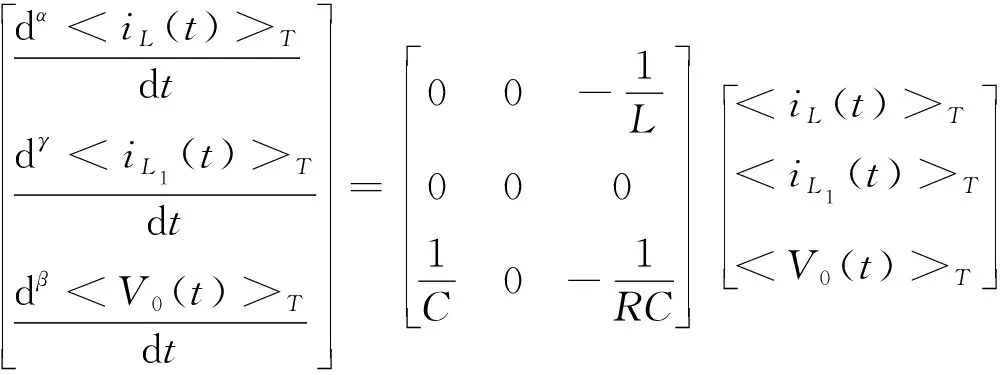
(10)

式中〈Vg(t)〉T、〈iL(t)〉T、〈iL1(t)〉T、〈V0(t)〉T、〈V1(t)〉T、〈d(t)〉T分别为一个开关周期内输入电压Vg、电感电流iL、谐振电感电流iL1、输出电压V0、谐振电感电压V1、占空比d的平均值,对各状态变量进行扰动:

(11)

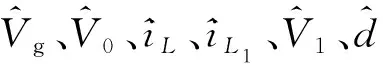
将式(11)代入式(10),分离直流分量,可得

(12)

根据Caputo分数阶导数的定义,常数的分数阶微分值为0,根据公式(10)可得到分数阶移相全桥变换器的交流小信号模型,如式(13)。

(13)

对式(13)进行分数阶Laplace变换,可得

(14)

(15)

(16)

根据上述结果,可以得出以下结论:移相全桥变换器的分数阶模型受到多个因素的影响,除了结构参数中的等效电阻、分数阶滤波电容、分数阶滤波电感、分数阶等效电感之外,电感和电容的阶次大小也会对分数阶模型产生影响;当分数阶阶次α=β=γ=1时,移相全桥变换器的分数阶模型与其整数阶模型的结果完全一致。这一结果显示,移相全桥变换器的整数阶模型可以被看作是其分数阶模型的一种特殊形式。

不同阶次下GVd(s)Bode图如图4所示。从图4中可以看出,当分数阶电感和电容的阶次改变时,对3个频段的影响是不相同的:在低频段,当阶次发生变化时,幅值波形和相位波形几乎没有变化;在中频段,分数阶电感和电容阶次减小,其幅频宽度增大,相角范围也随之改变;在高频段,分数阶电感和电容阶次减小,其幅频特性斜率减小,相角滞后范围减小。不同阶次下GVV(s)Bode图如图5所示,其变换规律与占空比到输出电压传递函数的变化规律相似。

图4 不同阶次下GVd(s) Bode图Fig.4 Bode diagram of different orders

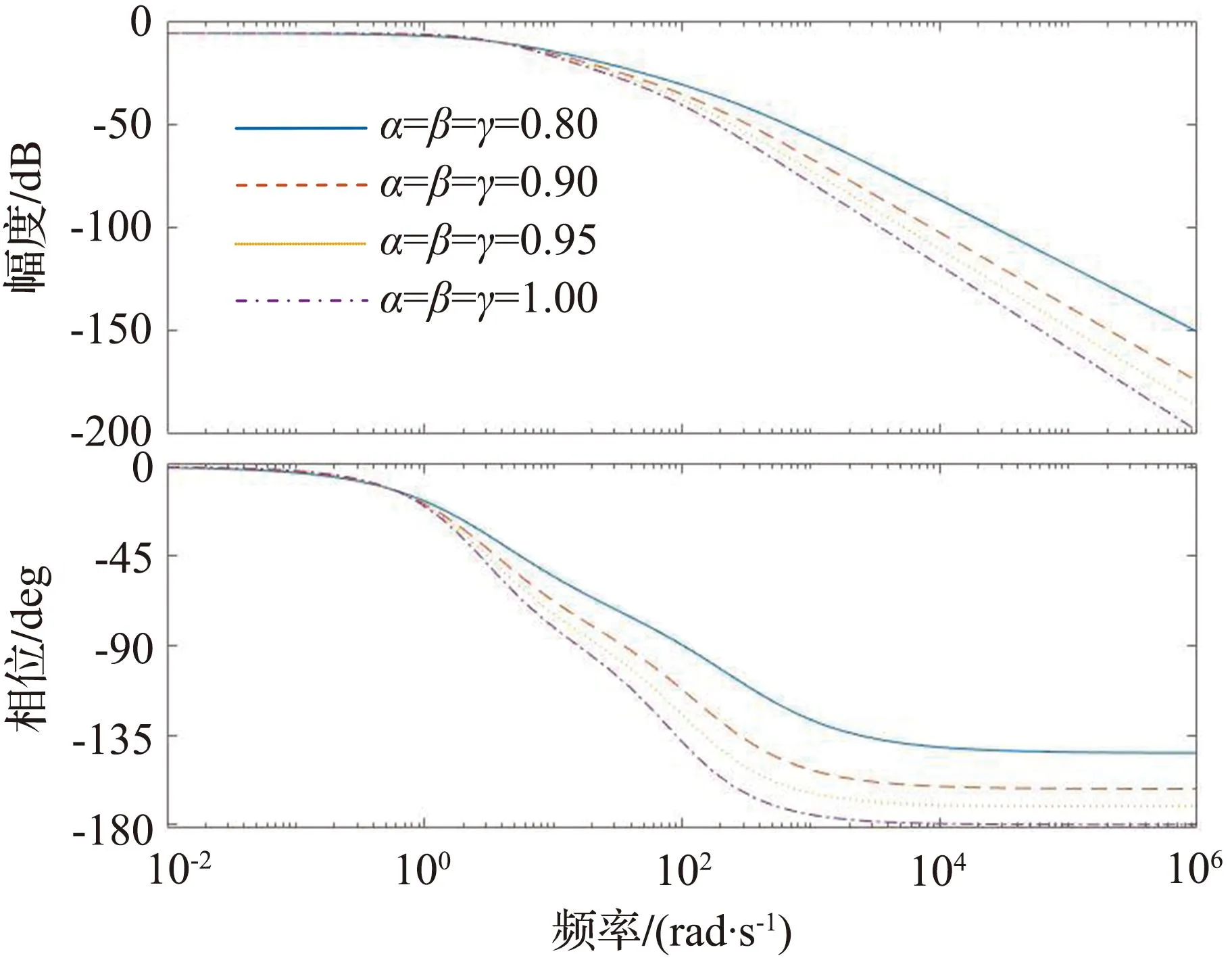
图5 不同阶次下GVV(s) Bode图Fig.5 Bode diagram of different orders

假设移相全桥变换器系统参数为:Vin=400 V,V0=48 V,n=10∶2,R=1.92 Ω,L=70 μΗ,Lr=43 μΗ,C=6 000 μF,开关频率fs=100 kHz,即开关周期T=10 μs,电感L的阶次记作α,电容C的阶次记作β,谐振电感Lr的阶次记作γ。图1中的关键元件是分数阶电感和电容的近似模型,根据文献[12]的研究,基于分抗链和改进的Oustaloup滤波器的分数阶微积分算法[13]可以用于建立分数阶电感和电容的等效电路模型[14],如图6所示。

(b) 分数阶电感等效模型图6 分数阶等效电路模型Fig.6 Fractional equivalent circuit model

0.8阶次分数阶电感、电容的等效电路参数见表1。

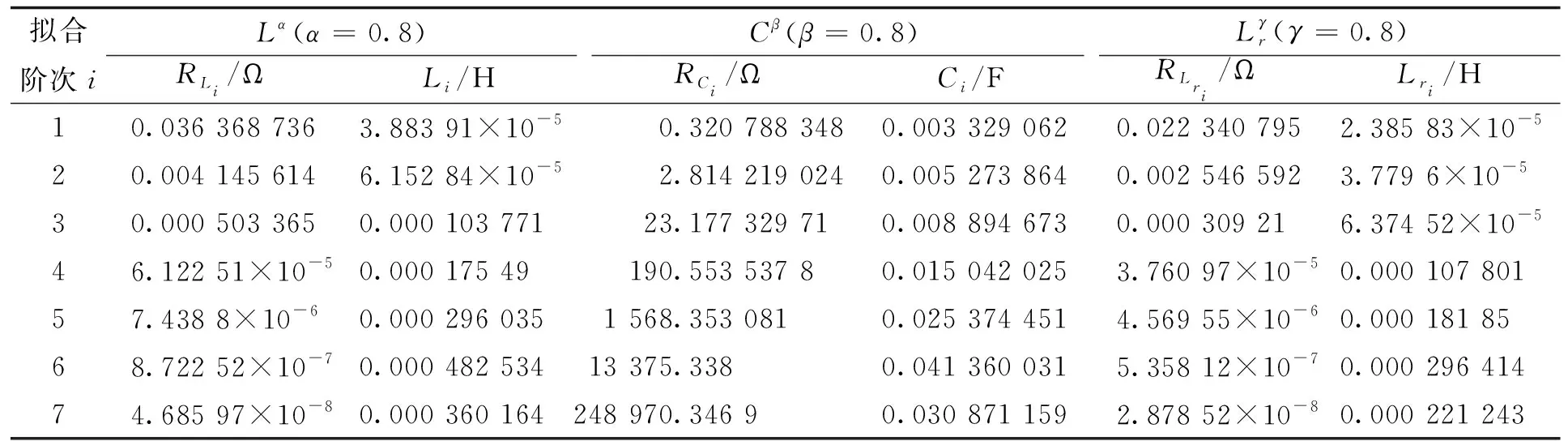
表1 0.8阶次电路参数Tab.1 0.8 order circuit parameters

通过构建不同阶次分数阶电感、电容的等效电路参数,将其在移相全桥变换器仿真模型中进行替换,得到不同阶次的仿真结果,图7为不同阶次的输出电压波形。从图7中可以看出,从高阶次到低阶次变化,系统的上升时间、调节时间明显逐渐变短,但是当阶次低于0.8阶之后,系统的超调变大,而电容为0.8阶时,输出电压稳定到48 V相较于其他阶次速度更快。通过观察经过放大后的不同阶次下电路仿真波形图可以看出,阶次变小,系统的电压纹波系数变大,虽然0.8阶次下的仿真模型输出电压纹波系数比整数阶略大,但对系统性能的影响不大。综上,本文分数阶电感阶次和分数阶电容阶次均取0.8阶,即α=β=γ=0.80。

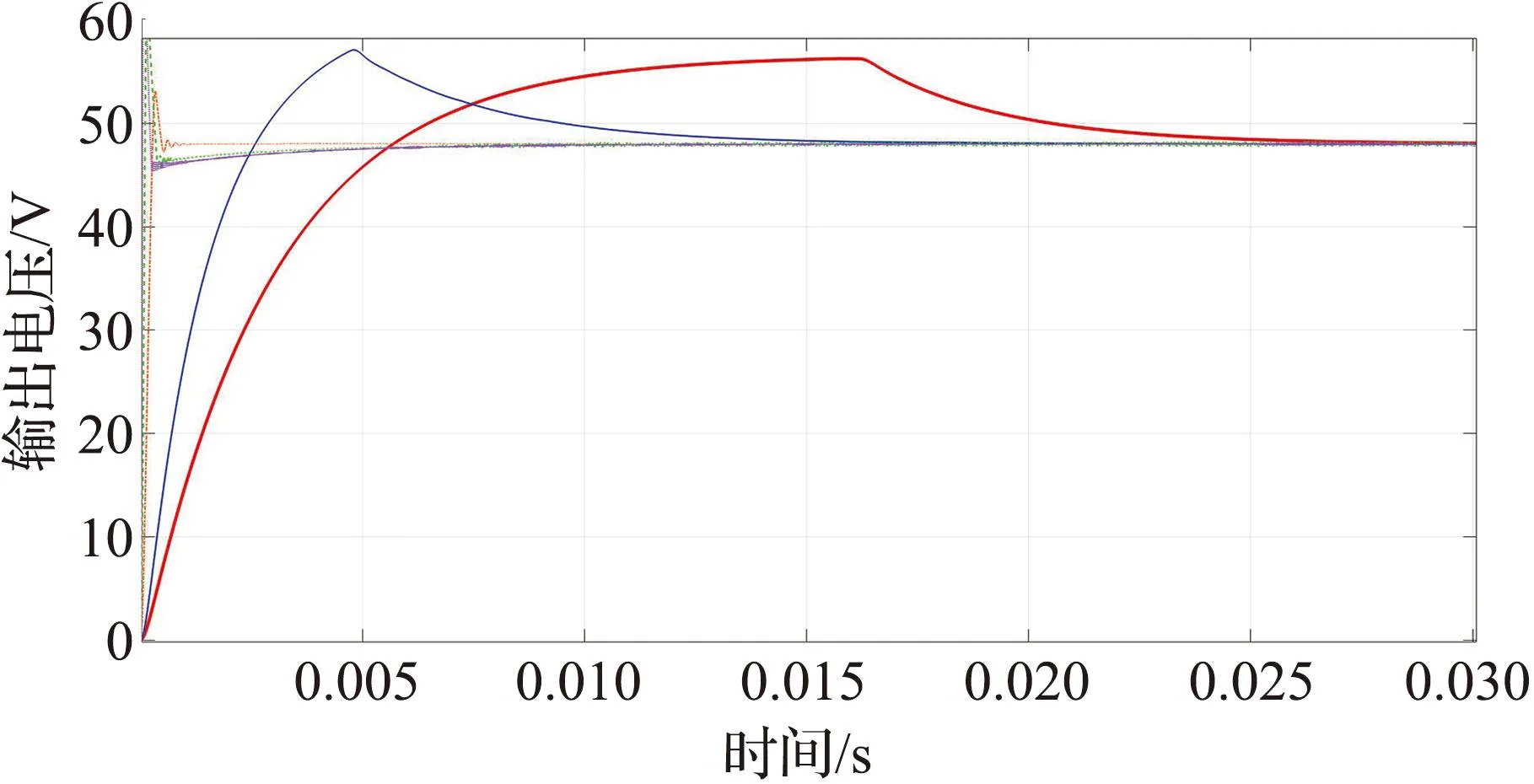
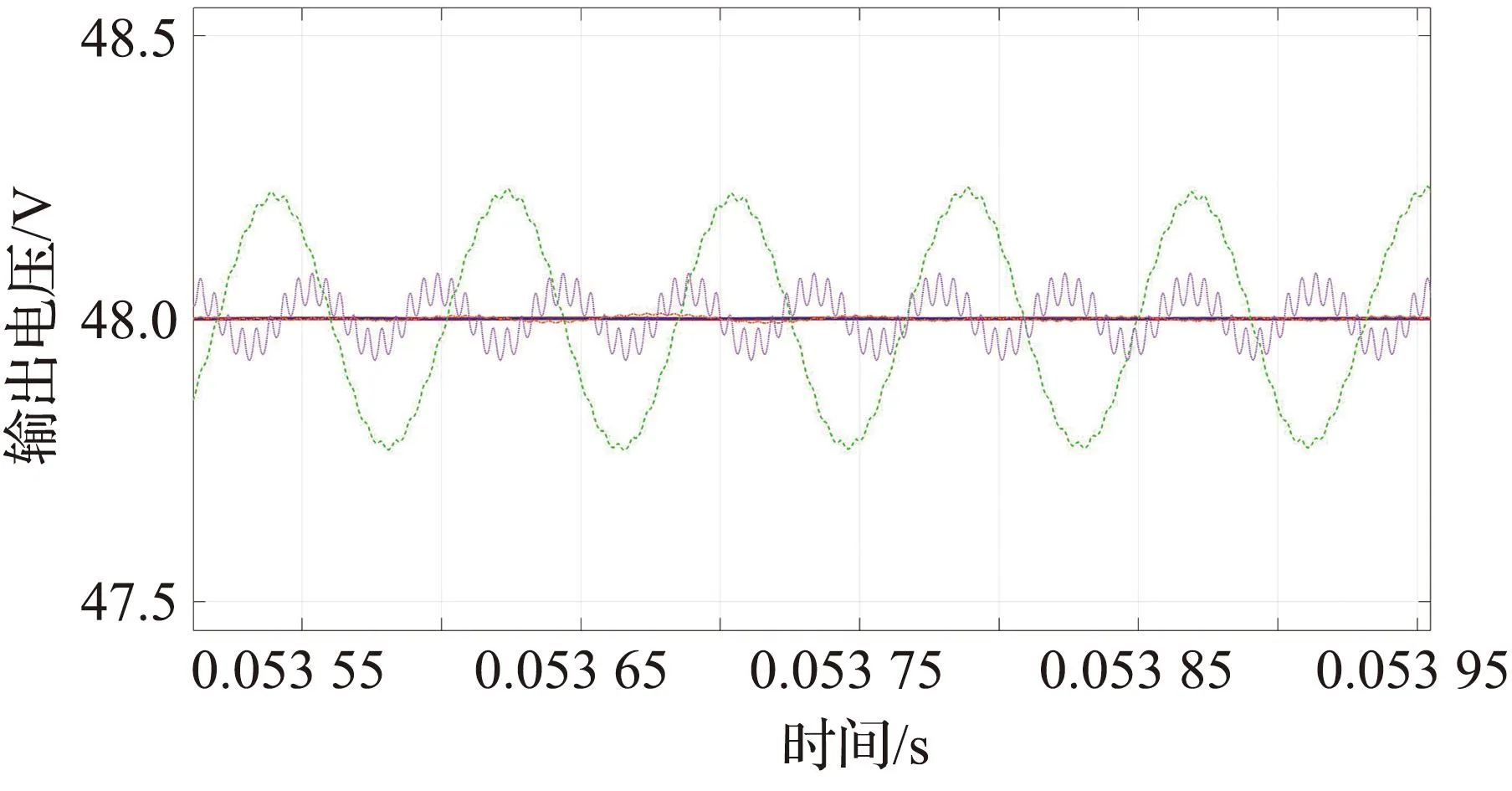
图7 不同阶次的输出电压波形Fig.7 Output voltage waveform at different orders

根据以上分析可知,分抗元件的阶次对系统的动态响应产生显著影响,降低分抗元件的阶次可以带来多方面优势,不仅可以加快系统的开环响应速度,减少超调量,还能显著缩短系统的调节时间。尽管分数阶元件的阶次不同,但系统的输出响应在一段时间后都能达到相同的稳态值。上述结果表明,分抗元件的阶次对系统的动态响应具有显著影响,但对系统的稳态值影响较小,通过选择合适的分数阶阶次,可以有效地调节系统的动态特性,从而满足不同应用场景的要求,为分数阶控制和系统设计提供了更丰富的选项和灵活性。

2 最优分数阶PIλ控制器设计

移相全桥变换器的输出电压V0往往受到多种因素的影响,包括输入电压Vin、负载电流I0以及变换器的结构参数等,这些因素的变化会导致输出电压的不稳定。为了提高移相全桥变换器输出电压的稳态精度和动态性能,在实际应用中通常采用反馈控制的方法。

随着分数阶微积分理论的深入研究,Podlubny教授发现对于被控对象为非整数阶时,采用分数阶控制器对其进行控制是必要的[8]。相较于传统PID控制器,通过引入2个可调参数λ和μ,使得分数阶控制器能够获得比传统控制器更优的控制效果,分数阶PIλDμ控制框图如图8所示。

图8 分数阶PIλDμ控制框图Fig.8 Fractional-order PIλDμ control block diagram

此外,随着各种智能优化算法的发展,可以实现灵活定制优化目标的控制器参数设计。为了进一步提高移相全桥变换器系统的运行性能,本文采用分数阶PIλ控制策略,通过智能算法对参数进行进一步优化,以获得最优的控制性能,其传递函数为

Gc(s)=Kp+Kis-λ,

(17)

式中:Kp为比例系数;Ki为积分系数;λ为积分阶次。假设分数阶PIλ控制器的输入、输出分别为e(t)、u(t),则

(18)

(19)

(20)

通过引入控制器Gc(s),分数阶移相全桥变换器的传递函数可以表示为

(21)

根据式(21),分数阶移相全桥变换器的性能与分数阶PIλ控制器参数(Kp、Ki和λ)的大小密切相关。考虑分数阶模型的非线性和复杂性,传统的频域分析方法无法获取最优参数。为了解决这个问题,普遍采用遗传算法作为一种全局寻优方法,以获得分数阶移相全桥变换器控制系统的最优性能,遗传算法具有全局搜索能力和操作方便性等优点,能够较好地处理非线性和复杂系统的优化问题。为了评估控制性能并选择最佳参数,常常采用误差积分准则,主要包括绝对误差积分(integral absolute error, IAE)、平均误差积分(integral square error, ISE)和ITAE等指标,它们的表达式可以表示为

(22)

由于IAE准则下难以确定最小系统误差,而ISE准则对误差过于灵敏而易产生振荡,ITAE准则综合考虑了时间、绝对误差和误差的积分,能够更全面地评估控制系统的性能,因此采用ITAE准则结合遗传算法作为控制器优化准则。为了避免控制器输出量u(t)太大导致系统不稳定,控制器参数优化目标函数定义为

(23)

式中的ω1、ω2为权值。

为了应对系统的超调问题,可以将超调量作为目标函数的考虑因素,即

(24)

式中的ω3为权值。

利用遗传算法来优化分数阶PIλ控制器的参数(Kp、Ki和λ),目标是找到使分数阶移相全桥变换器在式(23)或式(24)中的最优参数。通过这个过程,系统能够达到最佳的控制综合性能。为了更好地理解这一优化过程,可以参考文献[15]中给出的遗传算法优化过程示意图(图9)。该示意图具体展示了遗传算法在参数优化过程中的工作流程和关键步骤,有助于更好地理解优化过程中的各个环节。通过遗传算法的优化,能够找到最佳的控制器参数配置,从而实现系统的最优性能。

图9 遗传算法优化分数阶PIλ控制器示意图Fig.9 Schematic diagram of genetic algorithm PIλ optimization of fractional-order controller

3 仿真结果及分析

分数阶移相全桥变换器的电路参数见表2。

表2 分数阶移相全桥变换器电路参数Tab.2 Circuit parameters of fractional-order phase-shifted full bridge converter

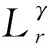
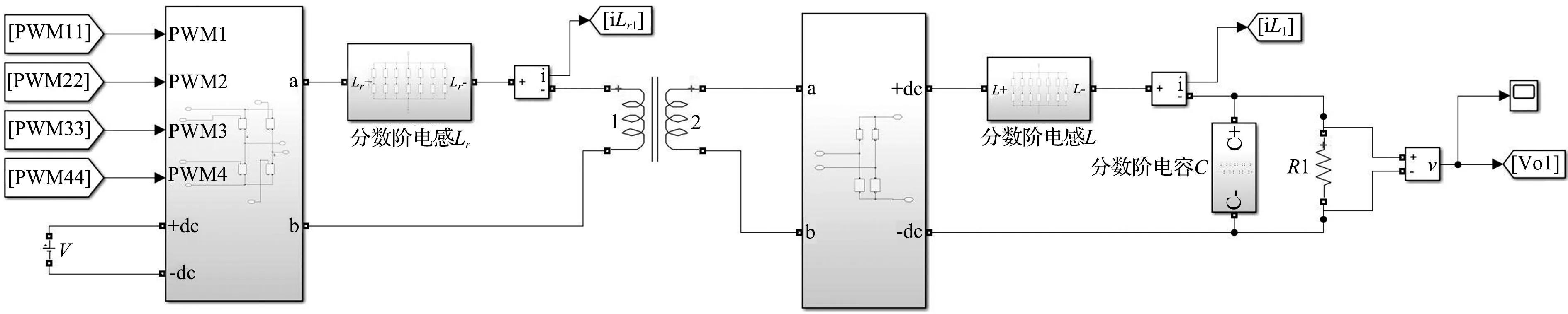
图10 分数阶移相全桥变换器仿真模型Fig.10 Simulation model of fractional-order phase-shifted full-bridge converter

基于分数阶PIλ控制和整数阶PI控制的分数阶移相全桥变换器控制系统状态响应如图11所示,系统的动态参数见表3。

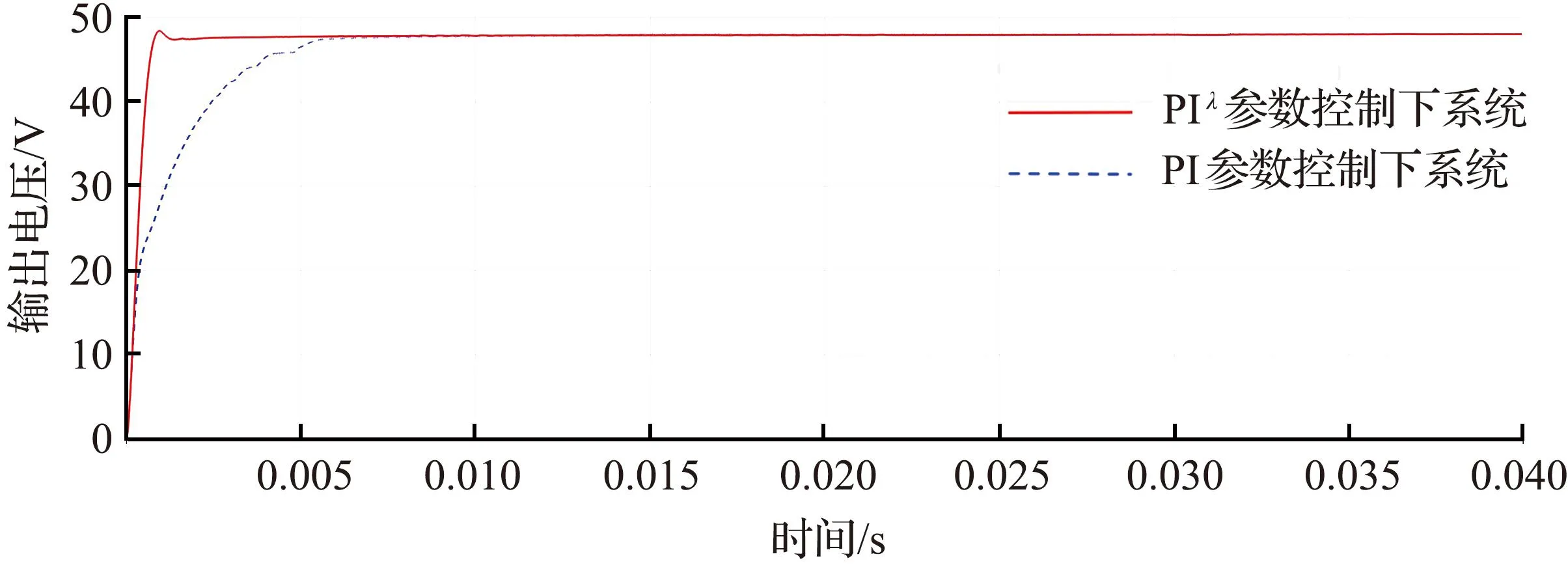
图11 不同控制方法下系统的阶跃响应Fig.11 Step response of the system under different control methods

表3 分数阶移相全桥变换器控制系统动态参数Tab.3 Dynamic parameters of the control system of fractional-order phase-shifted full-bridge converter

从图11和表3可以看出,与整数阶PI控制器相比,采用分数阶PIλ控制器可以带来更加显著的优势,显著减少系统的上升时间和调节时间,在经过短时的超调过程后,变换器快速到达期望的输出电压,超调量在5%以内。通过引入分数阶PIλ控制器,系统的控制性能和稳定性得到了显著的改善,使得系统能够更快速、准确地响应控制信号,从而提高了系统的整体效率和可靠性。而分数阶PIλ控制器的优越性在于其具备了可精确调节的分数阶微积分参数λ,使得分数阶PIλ控制器可以获得更优的控制效果。

系统稳定状态下,在仿真时间为0.02 s时施加系统等效负载扰动(通过并联一个同阻值大小的电阻R=1.92 Ω,使等效负载电阻减小),负载扰动时系统的动态响应如图12所示,负载扰动时系统的动态参数见表4。

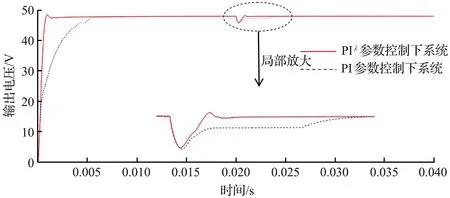
图12 负载扰动时系统的动态响应Fig.12 Dynamic response of the system under load disturbance

表4 负载扰动时系统的动态参数Tab.4 Dynamic parameters of the system under load disturbance

从图12和表4可以看出,当外部扰动发生时,分数阶PIλ控制下的移相全桥变换器具有更强的鲁棒性。在负载突然变化的时刻,分数阶PIλ控制器的应用使系统的输出电压在经历了微小的波动后能够迅速恢复到稳定状态,而且系统的动态降落和恢复时间都相对较小。这种控制策略赋予了系统较强的抗负载扰动能力,即使面对外界负载变化,系统也能够迅速调整输出电压,保持其稳定性,而整数阶PI控制下的系统恢复时间较慢,鲁棒性较差。

系统稳定状态下,在仿真时间为0.02 s时施加输入电压扰动(增大输入电压),输入电压扰动时系统的动态响应如图13所示,输入电压增大时系统的动态参数见表5。

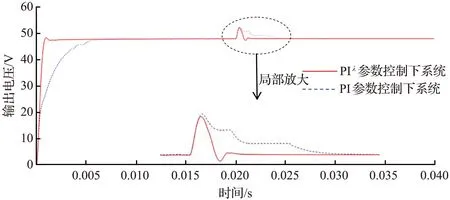
图13 输入电压扰动时系统的动态响应Fig.13 Dynamic response of the system with input voltage disturbance

表5 输入电压增大时系统的动态参数Tab.5 Dynamic parameters of the system when input voltage increases

从图13和表5可以看出,在仿真时间为0.02 s时进行输入电压扰动时,使输入电压由400 V升高到450 V,在采用分数阶PIλ控制器的系统中,动态降落现象较小,系统的输出电压V0经0.022 4 s调节后达到输出电压的期望值48 V。

在系统稳定状态下,在仿真时间为0.02 s时施加输入电压扰动(减小输入电压),输入电压扰动时系统的动态响应如图14所示,输入电压减小时系统的动态参数见表6。

图14 输入电压扰动时系统的动态响应Fig.14 Dynamic response of the system when the input voltage is disturbed

表6 输入电压减小时系统的动态参数Tab.6 Dynamic parameters of the system during voltage reduction

从图14和表6可以看出,在仿真时间为0.02 s时进行输入电压扰动时,使输入电压由400 V降低到350 V,在采用分数阶PIλ控制器的系统中,动态降落现象较小,系统的输出电压V0经0.022 2 s快速调节后达到输出电压的期望值48 V。

当系统面临输入电压增大或减小的扰动时,分数阶PIλ控制器能够快速作出调整,使得输出电压迅速恢复到设定值,这种优越的调节速度和抗干扰性能使系统能够有效地应对外界扰动,保持输出电压的稳定性和精确性。

根据前述控制系统的设计原则,当输出电压达到参考值后,在仿真时间为0.02 s时将期望输出电压由48 V增大为60 V,给定电压扰动时系统的动态响应如图15所示,给定电压扰动时系统的动态参数见表7。

表7 给定电压扰动时系统的动态参数Tab.7 Dynamic parameters of the system with a given voltage disturbance

从图15和表7可以看出,在采用分数阶PIλ控制器的系统中,参考电压发生改变时,突变瞬间系统输出有一定超调量,在5%以内,经小幅超调后系统稳定输出且调节时间比较短,系统的快速跟随性能良好。而在整数阶PI控制下,虽然参考电压发生改变时系统没有超调,但是系统的调节时间比较慢。

综合上述仿真分析,控制器结合遗传算法的优点,得到满足误差绝对值积分(ITAE指标)的最优分数阶PIλ控制器参数以及整数阶PI控制器的参数,分别对分数阶移相全桥变换器进行控制,并在仿真时间为0.02 s时刻对系统进行负载扰动、输入电压扰动以及给定电压扰动,通过对2种控制器下电路仿真模型的超调量、调节时间、恢复时间以及动态性能之间的比较,可以看到,分数阶PIλ控制器的灵活性和精确性使其能够更好地适应系统的特性和变化条件,能进一步提高系统的响应速度,因此,采用分数阶PIλ控制器的系统在动态性能和抗扰动能力方面具备明显的优势,能够有效地应对不同工况和负载变化的挑战,分数阶PIλ控制器控制下的分数阶移相全桥变换器的响应速度以及抗负载和输入电压扰动的鲁棒性更强。

4 结论

基于电感、电容实际阶次为非整数阶的特点,对分数阶移相全桥变换器的建模、分析和控制问题进行研究,得出以下结论:

① 利用状态平均模型推导得出分数阶移相全桥变换器占空比-输出电压、输入电压-输出电压的传递函数,通过绘制不同阶次下传递函数的Bode图与输出电压波形图,得出移相全桥变换器的频谱特性不仅与等效电阻、分数阶滤波电容、分数阶滤波电感、分数阶漏感的大小有关,而且与电感和电容的阶次密切有关,当分数阶阶次α、β、γ较小时,分数阶移相全桥变换器相对于整数阶移相全桥变换器表现出更卓越的性能。

② 结合分数阶微积分理论,基于所建立的分数阶移相全桥变换器模型,结合遗传算法的优点,利用ITAE误差积分准则将控制性能进一步优化,得到了ITAE指标最优的分数阶PIλ控制器以及整数阶PI控制器的控制参数。

通过对不同控制器参数进行整定,得到不同控制器对分数阶电路模型的性能比较,实验结果表明,相比于传统的整数阶PI控制器,分数阶PIλ控制器具备更出色的动态和稳态性能,能够有效减少系统负载扰动、输入电压扰动以及给定电压扰动的影响波动,进而实现更为稳定的控制效果,保持更好的抗干扰性能与更强的鲁棒性。