代码共享协议选择非合作-合作两型博弈模型①

李登峰, 江彬倩

(1. 电子科技大学经济与管理学院, 成都 611731; 2. 福州理工大学管理学院, 福州 350118)

0 引 言

新冠疫情的爆发与蔓延, 使得全球航空业遭到了史无前例的重创, 多家航空公司无法承受亏损, 已经申请破产保护, 例如, 澳洲第二大航空公司维珍澳洲航空、英国航空公司Flybe航空. 为有效防止疫情境外输入, 截止到2020年12月20日我国民航局已累计向中外航空公司发出“熔断”指令140次, 国际航空运输协会称预计全行业2020年将亏损1 185亿美元, 即每运载一名旅客将损失66美元. 为能在疫情下生存下来并保证航线的正常运营, 国内外许多航空公司纷纷选择进行合作, 而代码共享则是其中一种较为普遍的合作方式. 根据《国内航线航班代码共享管理办法》, 代码共享是指一家航空公司通过协议约定允许另一家或多家航空公司在其航班上使用各自航班代码进行经营行为. 国内外代码共享存在两种销售模式, 即包座销售代码共享与自由销售代码共享[1, 2]. 与包座销售代码共享相比, 自由销售代码共享不限制舱位销售数目, 且未售出舱位对应机票均可被任意航空公司销售, 是目前被采用较多的销售模式[3]. 然而, 相比于包座销售代码共享的研究[4-8], 自由销售代码共享研究非常少. 比如, Ito与Lee[1]仅对自由销售代码共享协议进行简单文字描述, 而未给出具体定价流程与模型刻画. 本文聚焦于自由销售代码共享协议优化选择与机票联合定价模型研究.

在航空业中, 机票定价一直是国内外学者关注的问题[9-14], 其中代码共享机票定价问题特别之处在于:若代码共享航空联盟享有反垄断豁免权, 则可选择单独定价或联合定价且共享利润. 对于单独定价的代码共享机票, Park[15]研究平行与垂直竞争的代码共享机票定价策略. Chen与Gayle[16]研究直飞航班与经停航班的代码共享机票竞争问题. Bilotkach[17]讨论低成本航空公司选择国内或国际航空公司作为代码共享合作伙伴时的定价策略. Oum等[18]与Lin[19]关注在包含价格领导者与跟随者的航空市场中各航空公司的定价策略. Hassin与Shy[20]考虑对代码共享机票具有不同偏好的乘客. 张辰与田琼[21]针对航空机票在线定价策略问题考虑了旅客忠诚度. 对于联合定价代码共享机票, Brueckner与Whalen[22]、Whalen[23]和Bilotkach[24]分析其定价策略, 但没有讨论联合定价后航空联盟利润如何分配. 郑士源与王浣尘[25]研究航空联盟横向与纵向联合定价, 但航空联盟利润是按照均分方式分配. Shen[26]提出以固定比例分配联盟利润的自由销售代码共享航空公司利润共享机制. Kimms与Cetiner[5]针对包座销售代码共享协议, 提出了航空联盟基于核仁的收益分配模型. 上述研究从不同角度对代码共享航空联盟定价策略进行分析, 但都忽略了一个关键性问题, 即代码共享协议是否能达成.

本文主要研究在利润共享机制下自由销售代码共享协议的优化选择问题. 按照决策时间顺序, 航空公司首先选择代码共享协议, 其次定价销售并获利, 其中联合定价的代码共享航空联盟可共享航空联盟利润. 由于上述过程包含了竞争与合作两种行为, 显然不同于文献[27-33], 这里的竞争与合作之间存在特定的耦合关联, 即航空公司为了最大化各航空公司最终所得利润, 代码共享协议是依据后续单独定价或联合定价的所得利润进行选择的, 因此非合作博弈或合作博弈都无法独立完整描述整个过程. 受Brandenburger与Stuart[34]提出的biform game概念启发, 本文创建一种新的博弈论研究范式:非合作-合作两型博弈. 非合作-合作两型博弈由非合作博弈部分与合作博弈部分按照先后固定顺序融通集成为一个统一的博弈. 这一研究范式的思想已结合具体管理情景, 开展了一些应用研究, 比如, 供应链库存管理策略选择[35-37]、双边链路形成策略优化[38, 39]与区块链共识达成[40]等. Hu等[4]对包座销售代码共享协议中的收益共享与舱位预定过程提出了两阶段博弈, 虽然同样包含了合作博弈与非合作博弈, 但博弈顺序与本文博弈顺序正好相反, 而且该两阶段博弈着重强调的是处理过程的阶段性, 并未关注收益共享与舱位预定之间的耦合关联性. 为此, 本文针对利润共享机制下的自由销售代码共享协议优化选择问题, 提出新颖的非合作-合作两型博弈模型, 并用非合作博弈部分、合作博弈部分分别描述航空公司选择代码共享协议与定价销售并获利过程, 显著不同于现有的所有研究工作, 如图1.

图1 非合作-合作两型博弈

针对代码共享机票定价的实际情景, 由于代码共享航空公司不一定能稳定地联合定价, 合作博弈中大航空联盟在不同竞争局势下可能是不同的, 并且一个航空联盟的利润(即特征值)会受其他航空联盟是否联合定价的影响, 即航空联盟的外部性. 这使得本文提出的非合作-合作两型博弈显著不同于现有所有研究工作[35-40]. 针对上述特点, 考虑到航空联盟最有可能的分裂过程, 本文构建了相应的合作博弈或带有层级结构合作博弈, 并利用Shapley值[41]或两步Shapley值[42]作为利润分配解, 验证了分配解的合理性. 为了更贴近现实, 本文还考虑了乘客对航空公司具有的不同偏好, 并细化了利润共享机制下自由销售代码共享机票定价过程, 这使得代码共享协议选择更具有说服力.

1 模型假设

考虑在两城市A与B之间直飞航线, 3家航空公司分别记作1、2与3, 可运营各自航班并销售该航线AB上的机票, 并将航空公司集合记作N={1,2,3}, 如图2所示.受Chen与Riordan[43]辐条模型启发, 本文构建了辐条模型, 用于描述乘客对航空公司的不同偏好, 如图3. 该辐条模型是由相交于一点O的三条线段L1O、L2O和L3O组成. 若点L与点L’同在线段LiO(i∈N),则符号|LL’|表示点L到点L’的距离;若点L与点L’分别在线段LiO与LjO, 则符号|LL’|表示线段|LO|与|OL’|距离的总和, 即|LL’|=|LO|+|OL’|. 线段LiO上的每个点表示第一偏好为航空公司i且第二偏好为航空公司j(j∈Ni)的一类乘客.

图2 直飞航线AB

由于每个乘客都有自己理想舱位, 虽然偏好某家航空公司的舱位, 但理想舱位与偏好航空公司的舱位可能存在一些偏好差异, 比如, 航程服务、航程时间以及舱位舒适度等. 这种偏好差异在辐条模型中通过乘客所在点与端点Li(i∈N)的距离体现. 设这些带有偏好的乘客均匀分布在线段上, 第一偏好为各家航空公司的乘客数相等, 即线段LiO长度相等且均为1, 即|LiO|=1(i∈N). 具体地, 位于线段LiO上的点L所对应乘客的理想舱位与其第一偏好航空公司i的舱位存在偏好差异|LiL|, 记作乘客(i,|LiL|), 而乘客(i,|LiL|)的理想舱位与第二偏好航空公司j舱位的偏好差异为|LjL|. 乘客(i,0)的理想舱位就是航空公司i的舱位, 与第二偏好航空公司j的舱位的偏好差距最大, 即|LiLj|=2, 称他们为最忠诚乘客(i,0). 对于乘客(i,1), 3家航空公司都是他的第一偏好航空公司, 相当于乘客(i,1)对3家航空公司没有偏好, 因此他们也被称为无偏好乘客(i,1). 除了这些最忠诚乘客, 乘客(i,|LiL|)的理想舱位与实际乘坐舱位都不一致. 当这些乘客最终购买任意一家航空公司舱位对应机票时, 他们需要克服一定的心理成本, 这使得他们对机票的支付意愿减小. 设最忠诚乘客(i,0)对航空公司i所售机票的支付意愿为vi, 无偏好乘客(i,1)比最忠诚乘客(i,0)需要克服心理单位成本t, 乘客(i,|LiL|)对航空公司i所售机票的支付意愿为vi-t|LiL|. 本文讨论的代码共享协议是在利润共享机制下, 因此航空公司可选择单独定价或联合定价. 设集合T(T⊆N)为联合定价的航空联盟, 并设pT为联合定价航空联盟所售机票价格. 为了方便叙述, 可将单干航空联盟{i}与航空联盟N{i}分别简记为i与Ni.航空公司i单独定价时, 所售机票价格记为pi.由于乘客对航空公司i舱位的效用随着机票价格升高而减少, 乘客(i,|LiL|)对航空公司i舱位的效用表示为

(1)

为简化问题, 提出以下假设.

假设1由于航空公司品牌知名度越大, 乘客的支付意愿越高. 最忠诚乘客(1,0)对所售机票的支付意愿为v, 且品牌知名度参数为θ(0<θ≤1),最忠诚乘客(2,0)(或(3,0))所售机票支付意愿相等, 即v1=v,v2=v3=2θv.航空公司与其他品牌知名度相当的航空公司代码共享合作中, 更容易在服务水平、机票定价、品牌建设与乘客福利等方面达成一致意见. 因此, 知名度相当的航空公司更容易达成航空联盟. 此外, 航空公司代码共享合作难易程度还受航线覆盖范围、航班调度决策与内部股权关系等因素的影响.本文假设在两家航空公司组成的联合定价航空联盟T(T⊂N,|T|=2)中,较容易达成航空联盟首先是知名度相当的航空公司2与航空公司3, 其次是航空公司1与航空公司3,再次是航空公司2与航空公司3.

根据上述假设1, 当0<θ<0.5时, 则航空公司1比航空公司2与航空公司3更知名;当θ=0.5时, 则航空公司1、航空公司2与航空公司3品牌知名度相同;当0.5<θ≤1时, 则航空公司2与航空公司3比航空公司1更知名.

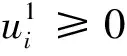
为满足假设2, 设航空公司联盟T(T⊆N)的机票价格pT满足

(2)

(a) (b)

当各个航空公司i(i∈N)分别单独定价时, 则可以推导出乘客对航空公司的偏好差异分别为

xij=(vi-vj+pj-pi)/(2t)+1,

xik=(vi-vk+pk-pi)/(2t)+1

(3)

不妨假设航线的市场占有率为1. 由于辐条模型的总长度为3, 容易得到, 辐条模型的密度为1/3, 则任一航空公司i(i∈N)的市场占有率为qi=(1/2)×(1/3)×(xij+xik), 即

qi=(2vi-vj-vk+pj+pk-2pi)/

(12t)+1/3

(4)

类似地, 当两家航空公司i与j(i,j∈N)联合定价时, 则可得乘客对航空公司的偏好差异分别为

xij=(vi-vj)/(2t)+1,

xik=(vi-vk+pk-p{i,j})/(2t)+1,

xjk=(vj-vk+pk-p{i,j})/(2t)+1

(5)

此时各个航空公司的市场占有率分别为

qi=(2vi-vj-vk+pk-p{i,j})/(12t)+1/3,

qj=(2vj-vi-vk+pk-p{i,j})/(12t)+1/3,

qk=(2vk-vi-vj+p{i,j}-pk)/(12t)+1/3

(6)

航空联盟{i,j}的市场占有率为q{i,j}=qi+qj.

同样地, 当3家航空公司联合定价时, 则可得乘客对航空公司的偏好差异分别为

x12=x13=(1-2θ)v/(2t)+1,x23=1

(7)

此时各个航空公司的市场占有率分别为

q1=(1-2θ)v/(6t)+1/3,

q2=q3=(2θ-1)v/(12t)+1/3

(8)

2 非合作-合作两型博弈模型构建

2.1 非合作博弈部分

表1 非合作博弈部分3家航空公司形成的可行竞争局势

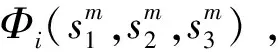
(9)

结合式(1)、式(3)、式(5)与式(7)可推出不同定价合作形式下不同乘客总剩余, 记作SmP. 在竞争局势Sm下, 社会总福利记做WmS, 由航空公司总利润PmA与乘客总剩余SmP两者组成, 即WmS=PmA+SmP.

2.2 合作博弈部分

航空公司要在非合作博弈部分中选择、确定纳什均衡局势, 需要预测3家航空公司在合作博弈部分中在不同竞争局势下所获得的利润. 本文讨论的是利润共享机制下的代码共享协议, 不妨假设代码共享航空公司可选择单独定价或联合定价, 非代码共享航空公司只能单独定价并获得各自的利润, 联合定价的航空公司将分得部分航空联盟利润, 单独定价航空公司所获得利润归各自所有. 具体地,从定价销售与共享利润两个过程进行研究.

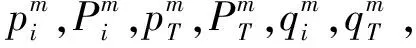
(10)

(a) (b)

(11)

(a) (b) (c)

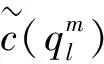
(12)

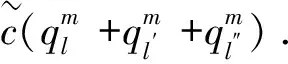
(13)

(a) (b) (c) (d) (e)

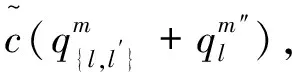
(14)

(15)

(16)

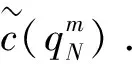
(17)

其次是共享利润. 在第一类竞争局势下, 由于没有代码共享航空联盟, 航空公司不能共享利润. 在第二类或第三类竞争局势下, 虽然存在代码共享航空联盟, 但代码共享航空联盟中的航空公司一旦意识到形成联合定价的大航空联盟不如形成单独定价的航空子联盟, 那么该航空联盟不稳定, 并且该航空联盟最有可能实现的分裂可描述为单干划分, 则航空公司也不能共享利润. 综上, 共享利润的充要条件为存在稳定的代码共享航空联盟, 或存在不稳定的代码共享航空联盟, 并且最有可能实现的分裂不是单干划分.

在非合作博弈部分中, 由于代码共享协议决定了航空公司之间长期合作关系, 选择代码共享协议应以稳定联合定价时的最优利润作为依据. 下面先给出了航空联盟稳定与最优划分的概念. 由于单干航空联盟无法再分裂, 因此一定是稳定的. 对于非单干航空联盟, 是否稳定取决于该航空联盟分裂后的航空子联盟能否获得更多利润. 于是, 若非单干航空联盟T(|T|≥2)所得最优利润不小于除了零划分以外的其余任意划分下航空子联盟的之和, 即

(18)

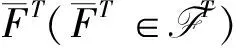
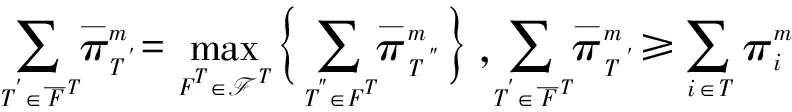
(19)

(20)

则划分{{1,3},{2}}比{{1,2},{3}}更有可能实现.

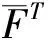
(21)

利用Shapley值分配方法, 可得航空公司i(i∈TP)在合作博弈部分所得利润分别为

(22)

υ(T)≥υ(i)+υ(Ti)

容易得到, 通过Shapley值分配所得航空公司的利润满足:集体有效性(即大航空联盟利润全部分配完、没有剩余)与个体合理性(每家航空公司分得的利润不小于单干时的利润), 即

(23)

这说明, 按照上述Shapley值分配过程进行航空公司利润分配是合理、有效的.

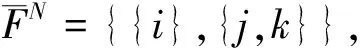
(24)

利用两步Shapley值分配方法对层级结构合作博弈(N,υ,L)进行求解. 具体地, 将航空联盟{i}与{j,k}分别视为两个整体, 记作[{i}]与[{j,k}], 此时大航空联盟仅包含两家航空公司[{i}]与[{j,k}], 记作⎣N」. 首先利用Shapley值分配方法, 将大航空联盟的利润υ(N)分配给两家航空公司[{i}]与[{j,k}];再利用Shapley值分配方法, 将航空联盟{j,k}的υ({j,k})分配给两家航空公司j与k, 航空公司j与k还能得到航空联盟{j,k}分给的利润与的差值Sh[{j,k}](⎣N」,υ)-υ({j,k}), 即3家航空公司在合作博弈部分所得利润分别为

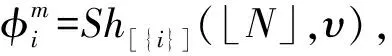
(25)

结合式(19)、式(20)、式(24)与式(25)可得, 两步Shapley值分配所得的利润满足:集体有效性与个体合理性, 即满足式(23), 因此利用上述两步Shapley值分配航空联盟的利润也是合理、有效的.

若航空联盟TP包含3家以上航空公司, 则类似可得航空联盟最有可能的分裂过程, 航空公司i(i∈TP)利用多步Shapley值[45]可得到相应的利润, 并可类似证明, 基于多步Shapley值的航空公司利润分配是合理、有效的. 不过, 因为航空联盟TP最多包含3家航空公司, 从而最多经过两次划分, 即r≤2,所以不涉及这种情形.

3 非合作-合作两型博弈模型求解

方法

在上述非合作-合作两型博弈模型中, 非合作博弈部分中航空公司的利润需要从合作博弈部分中分配得到, 因此需要先求解合作博弈部分的利润分配, 才能求解非合作博弈部分的纳什均衡局势.

3.1 合作博弈部分的求解方法

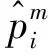
而运营总成本设为所有运营成本之和, 并记为

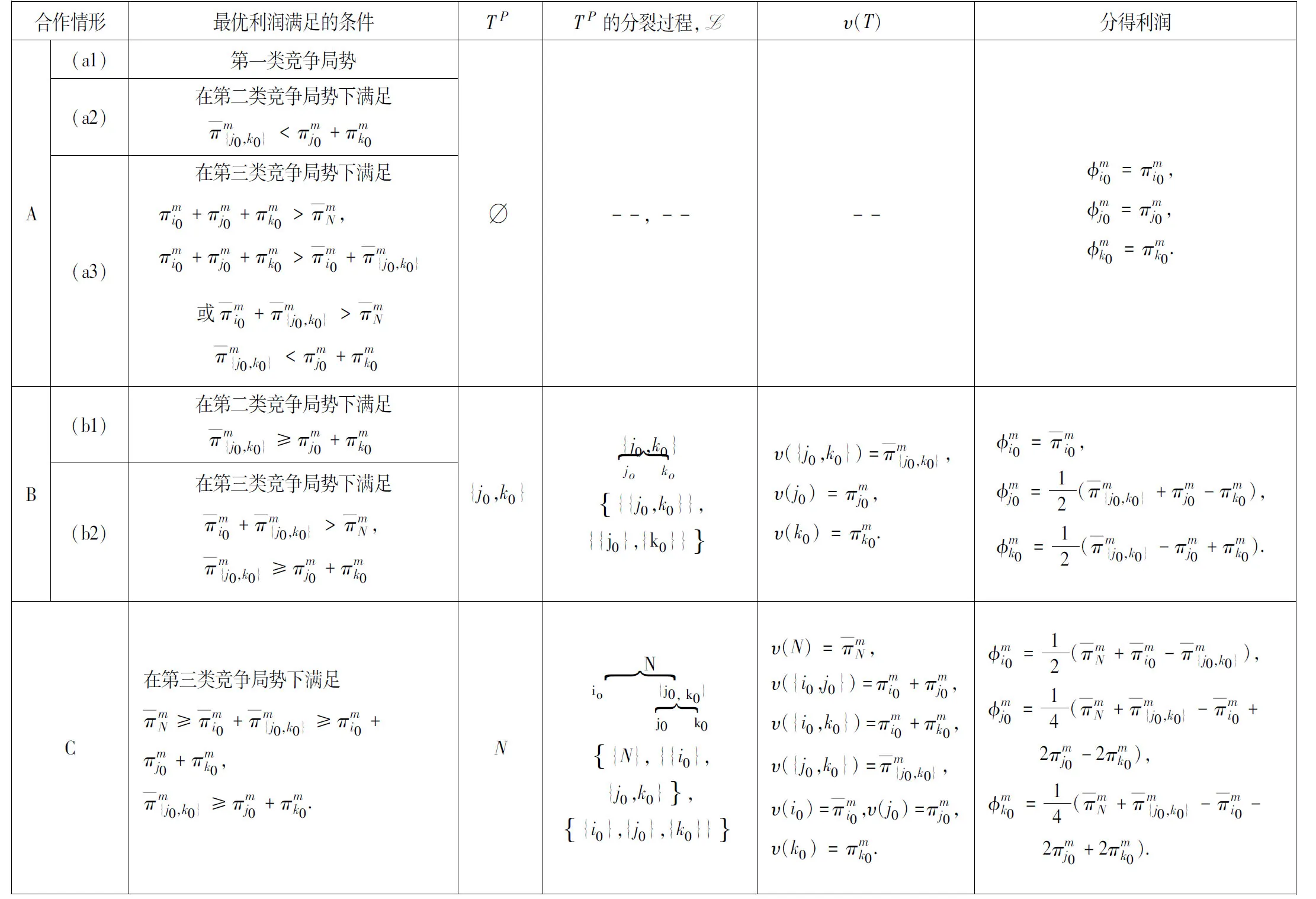
表2 合作博弈部分中的不同合作情形

续表2

3.2 非合作博弈部分的求解方法

由假设1可知, 航空公司2与航空公司3是对称的. 例如, 当航空公司1选择非代码共享航班时, 航空公司2选择市场方(或承运方)的情形等价于航空公司3选择市场方(或承运方)的情形, 可推出

(26)

因此, 本文只需要考虑竞争局势S0、S1、S3、S5、S6与S8下航空公司的最优利润, 可得到在非合作博弈部分中所有可能竞争局势下所有航空公司的利润, 如表3.

表3 非合作博弈部分中所有可行竞争局势下航空公司的利润

结合式(9)与表2, 可得如下定理1.

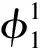
3.3 非合作-合作两型博弈模型求解方法与过程

对于上述自由销售代码共享协议优化选择非合作-合作两型博弈模型, 可以总结其求解方法与过程如下:

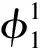
4 数值实例分析

表4 合作博弈部分的结果

表5 利润共享机制与利润独享机制下非合作博弈部分航空公司的利润

在表4与表5中, 对比利润共享机制与利润独享机制下的代码共享航空公司的结果可得:1)从票价上看, 未达成代码共享协议的竞争局势S0下市场平均票价最低;航空公司达成代码共享协议后, 与竞争局势S0的市场平均票价相比有所提高;若航空公司进一步联合定价并利润共享, 则市场平均票价虽仍高于竞争局势S0的市场平均票价, 但低于单独定价时的市场平均票价, 即

为进一步体现利润共享机制差异, 下面从3家航空公司、所有乘客以及乘客与航空公司的角度分别对所有竞争局势进行分析. 如图8所示, 其中两个柱体之和表示社会总福利, 柱体上的数值表示相应竞争局势中的乘客总剩余、航空公司总利润或社会总福利.

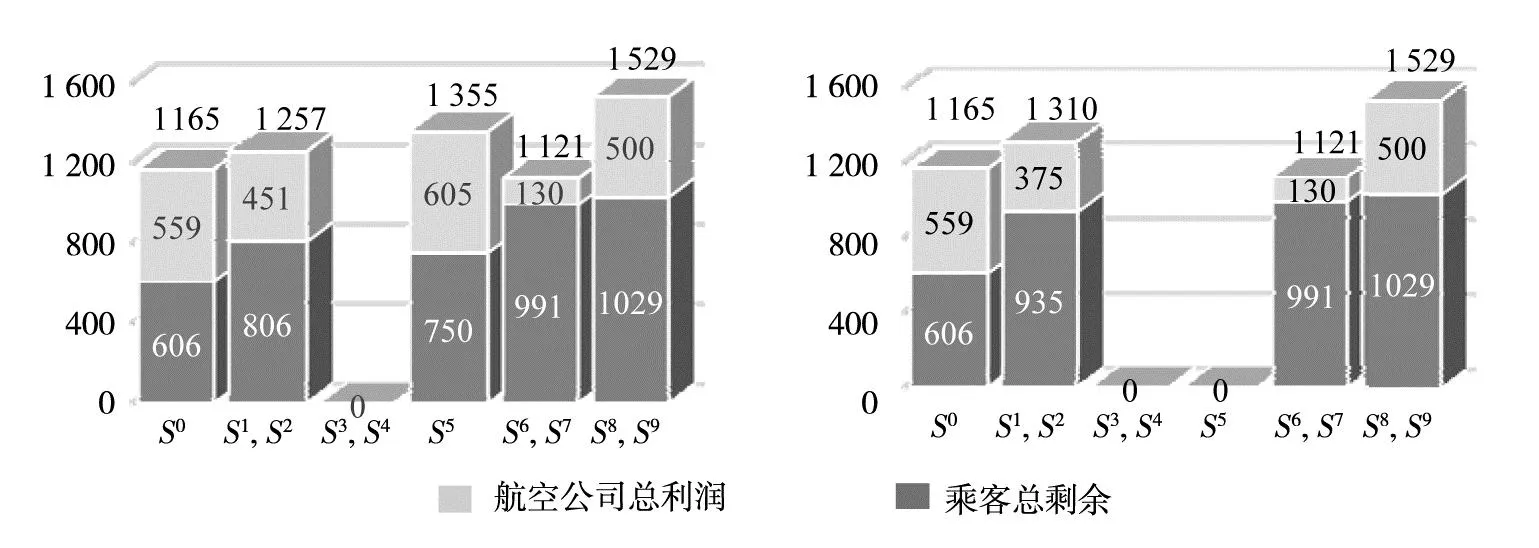
(a)在利润共享机制下 (b)在利润独享机制下

一方面, 利润共享机制改变了较优纳什均衡局势. 利润独享机制下, 较优纳什均衡局势为竞争局势S1与S2, 即政府从最大化社会总福利的角度将支持较不知名的航空公司2与航空公司3达成代码共享协议;利润共享机制下, 竞争局势S5的社会总福利高于所有纳什均衡局势, 较优纳什均衡局势转变为竞争局势S5, 即政府将支持3家航空公司达成代码共享协议, 并且较知名的航空公司1作为承运方. 另一方面, 利润共享机制改变了较优纳什均衡局势下的乘客总剩余、航空公司总利润与社会总福利. 对比利润共享与独享下的较优纳什均衡局势(即利润共享下的竞争局势S5与利润独享下的S1和S2), 虽然乘客总剩余减少了19.8%, 但航空公司总利润增长了61.3%, 社会总福利增长了3%, 这说明在本例中采用利润共享机制下更有利于整个社会.

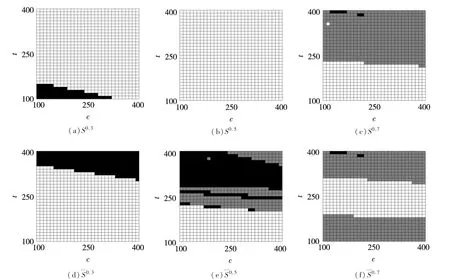
图9 利润共享机制与利润独享机制下较优纳什均衡局势Sθ与中的所属竞争局势类别

图10 实施利润共享机制后的社会总福利WθS与社会总福利变化量WθDS

5 结束语

应用辐条模型描述乘客对航空公司的不同偏好, 进而针对利润共享机制下自由销售代码共享协议的选择过程, 构建了非合作-合作两型博弈模型. 由于联合定价航空联盟在不同竞争局势中可能不一样, 且这些航空联盟具有外部性, 本文根据最有可能的分裂过程, 确定了最大联合定价航空联盟与各航空子联盟的特征值(利润), 并应用Shapley值与两步Shapley值分配方法, 获得航空公司在利润共享机制下的最优利润. 还应用数值实例验证了非合作-合作两型博弈模型能够有效地解决利润共享机制下自由销售代码共享协议的优化选择问题, 同时该模型还能预测各航空公司在选择代码共享协议后定价策略以及所获利润. 通过对票价、市场占有率、航空联盟总利润、运营总成本、纳什均衡局势、航空公司总利润、乘客总剩余与社会总福利等多方面的比较得知, 利润共享机制下自由销售代码共享协议是有优势的, 特别在只存在一家较知名航空公司的航空市场中更加明显. 本文主要对直飞航线上自由销售代码共享协议优化选择进行研究, 实际中中转航线上也存在自由销售代码共享协议, 将来会对这个问题进行深入研究. 另外, 代码共享属于共享经济的范畴, 受文献[46,47]启发, 结合政府干预或区块链的代码共享协议也是本文未来的研究方向.