PSM-DID在政策评价中的应用现状与改进方法①

蔡 俊, 杨 岚, 周亚虹

(1. 华中科技大学管理学院, 武汉 430074; 2. 西南财经大学统计学院, 成都 611130 ;3. 上海财经大学经济学院及上海财经大学滴水湖高级金融学院, 上海 200433)

0 引 言

最近十几年来,倾向得分匹配-双重差分(propensity score matching-difference in differences, PSM-DID)在政策评价因果效应识别和估计中得到了越来越多的关注.倾向得分匹配的基本原理是,将原本基于多维控制变量的处理组和控制组的匹配转变为基于一维倾向得分的匹配,从而使匹配维度大大降低,而匹配质量和效果却得到显著提升.基于匹配后的样本进行分析,能够克服样本自选择偏差,从而使得因果估计更为准确.而双重差分则可以通过控制时间和个体两个维度的不可观测异质性,在反事实的框架下来评估政策发生和不发生这两种情况下被观测结果的变化,得到因果推断.

本文统计和梳理了自2012年—2022年间国内部分经济学管理学权威期刊,即《经济研究》、《管理世界》、《管理科学学报》、《经济学(季刊)》、《世界经济》、《中国工业经济》中使用了倾向得分匹配的文章.在这十年间,共有169篇文章使用了倾向得分匹配方法,其中118篇将其作为主回归或者主回归之一,51篇使用该方法进行稳健性检验.通过文献梳理,本文发现:

第一,倾向得分匹配在经济管理各个领域的应用都较为广泛,特别是在政策评估时成为一种重要的因果效应估计方法而广为人知.由于通常能获取到的数据大多为观测数据,利用观测数据进行政策评价时首先要解决的问题就是样本的自选择性,而倾向得分匹配能够在利用已有数据的基础上较好的处理样本的自选择性.例如:孙亮等[1]采用PSM-DID方法,系统考察了我国资本市场中政府赋予型声誉的激励效果和作用机理.黄俊等[2]以第一巡回法庭和第二巡回法庭管辖范围内的上市公司为实验组,采用PSM方法构建对照组样本,探究巡回法庭的设立对企业投资的影响.吴要武[3]基于PSM方法估计跨省迁移者相比于省内迁移者真实的收入优势.贾俊雪和秦聪[4]利用2 126个村庄的调查数据进行倾向得分匹配实证检验,识别专业协会建立对处理组农户人均纯收入的平均处理效应.

第二,倾向得分匹配方法常与双重差分法结合使用.由于原理和模型设置容易理解和运用,双重差分法成为政策效应评估方法中的最流行的方法之一.十年间,使用倾向得分匹配-双重差分法(PSM-DID)进行反事实估计的文章有107篇,占到发文总数的63.3%(其中宏观政策效应评估有22篇,占20.6%;微观政策效应评估有85篇,占79.4%).例如:宏观政策层面的分析中,万海远和李实[5]采用倾向得分匹配与双重差分的方法来构造反事实,从而在拟实验环境下评估户籍歧视对城乡收入差距产生的影响.王庶和岳希明[6]使用PSM-DID评估退耕还林在农民增收、非农就业和扶贫开发等方面的政策效果.龙玉等[7]利用PSM-DID模型考察在高铁开通前后的高铁沿线各城市风险投资项目和投资金额的变化,来检验高铁对风险投资区域特征的影响.微观政策层面的分析中,孙文凯和王乙杰[8]采用PSM-DID方法估计父母外出务工对留守儿童自评健康的影响.张杰等[9]利用PSM-DID模型系统地检验了出口与生产率的关系.王桂军和张辉[10]使用PSM-DID评估了“一带一路”倡议对中国OFDI企业全要素生产率的影响.

第三,倾向得分匹配作为一种数据预处理方法,能让处理组和对照组的可观测特征尽可能接近,从而克服样本自选择带来的估计偏误,但是使用倾向匹配得分需要满足两个前提:一是平衡性假定,在计算倾向得分后,需要评估匹配的质量如何,即检验可观测特征是否均衡;二是共同支撑假设,也即评估控制组和处理组倾向得分的分布,若两组样本没有重合的倾向得分,或者重合的样本量太小,就会导致无法匹配或匹配偏差较大.在梳理文献时,本文发现仅有82篇文章(占比48.5%)在正文中汇报了平衡性假定检验的结果,有29篇文章(占比17.2%)未汇报具体检验统计指标,仅指出通过该检验或者检验结果备索,有58篇文章(占比34.3%)未进行平衡性检验.同时,本文还发现,十年间文献进行平衡性检验基本都是基于比较处理组和对照组样本均值是否存在统计意义上的差异,若两组的均值差的t统计量显示实验组和对照组均值没有显著差异,则认为通过平衡性检验,使用倾向得分匹配后得到的样本较为均衡.但是,仅仅基于均值的差异判断两组样本的平衡性较为片面,一种可能的情况是虽然均值较为接近,但是方差差异很大,例如处理组的方差较小,控制组的方差较大,此时,将两组进行比较得出的结论有较大偏差.因此,本文认为目前文献中广泛使用的平衡性检验方法存在不足,需要进行更多维度平衡性检验指标的检测,只有确保处理组和对照组的样本实现平衡后,基于匹配后的样本所估计的因果效应才有意义[11, 12].

鉴于该方法的广泛应用性和既有研究的不足,本文在梳理国内既有使用倾向得分匹配的文章的基础上,首先对目前广泛使用的平衡性测度指标进行总结,对文献中普遍使用的均值差t检验方法进行回顾并说明其缺陷,然后推荐了六种多维度测度指标,分别基于标准化距离和分位数距离的视角对平衡性进行测度.第二,利用两个实例(一个微观层面的实证分析,一个宏观层面实证分析)说明和验证既有平衡性测度指标的不足,并计算新的平衡性测度指标,基于这些指标判断样本间的平衡性,研究发现均值差t检验可能将非平衡的样本判定为平衡,因此单纯基于均值差t检验判定平衡性比较片面且可能有误导性.第三,若样本匹配后在多种平衡性测度指标的判断下显示为不平衡,传统估计方法将有较大偏误,本文创新性地提出了一种新的更稳健的估计方法:倾向得分匹配-逆概率加权-双重差分(PSM-IPW-DID),并基于蒙特卡洛模拟比较本文提出的PSM-IPW-DID估计量与传统PSM-DID估计量的优劣.最后对两个实例使用该新方法重新进行分析,以进一步说明使用PSM-DID和PSM-IPW-DID方法时估计结果的差异.

因此,本文的创新性体现在:一是明确指出既有文献中广泛使用的平衡性测度指标的不足,并给出了更为全面的平衡性测度指标.二是提出适用于非均衡样本的新的估计方法:倾向得分匹配-逆概率加权-双重差分(PSM-IPW-DID).逆概率加权(inverse probability weighting, IPW)由于其基于样本对总体的还原,可以使模型推断结果具有总体代表性,被广泛地应用于缺失数据时的统计分析和因果推断的计量估计中[13-15].文献中已有证据表明在倾向得分重合度(overlap)较好时,IPW方法比PSM方法占优(有更小的方差);在倾向得分重合度比较差时,PSM比IPW更稳健[16-18].本文提出的新方法结合倾向得分匹配和逆概率加权的长处,规避其短处,在不进一步删除样本的情况下得到一种综合更稳健的双重差分估计方法.另一方面,已有的文献或是单纯比较倾向得分匹配和倾向得分逆概率加权的联系与区别,如King 和Richard[19];或是探讨在一般回归模型中考虑倾向得分的使用,如Wooldridge[20]中的逆概率加权-回归调整的估计量(IPWRA);本文将PSM-IPW与DID回归模型结合起来,既考虑倾向得分重合度(overlap)对估计的影响,也为平衡多维控制变量提供了新的思路.(1)最新的相关文献为 Arkhangelsky和Imbens[21],他们发现在存在组间异质性时,逆倾向得分加权使固定效应模型估计值更加稳健.

1 平衡性的测度

本节首先介绍文献常用的平衡性检验实施方法,然后推荐6种本文认为应该更多关注的多维度平衡性测度.

1.1 文献中常用的平衡性检验

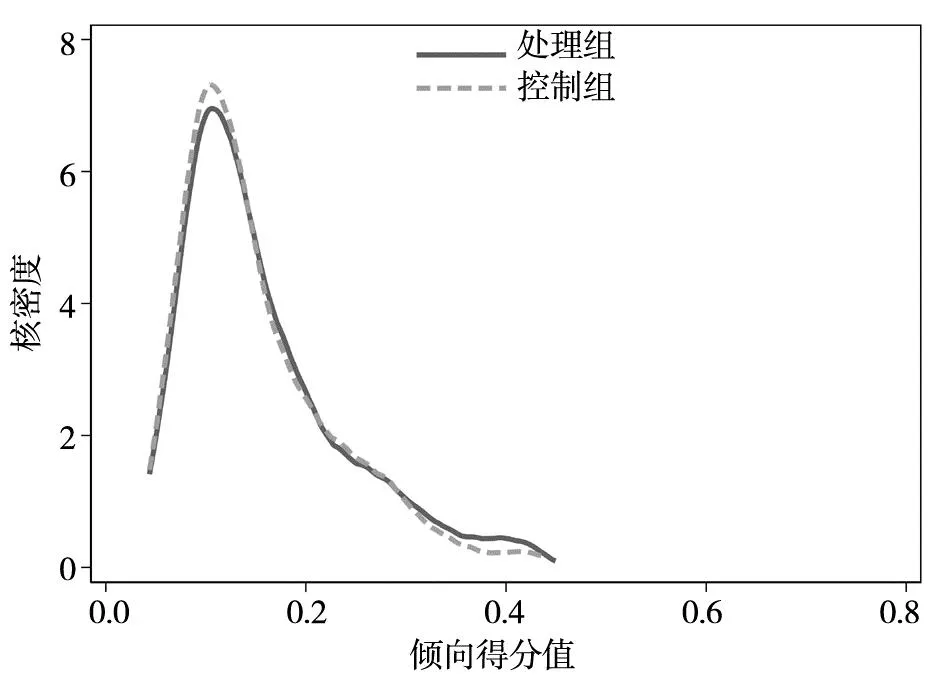
基于对既有文献的梳理和总结,本文发现既有文献一般将倾向得分匹配后样本每一个控制变量的处理组和控制组之间的加权均值差异(mean difference)进行t检验,以此作为平衡性检验.文献中该方法的流行得益于Stata中pstest命令的便利性,该命令输出结果呈现了各变量匹配前后的均值,并输出加权均值差t检验的结果(如表1).(2)Stata程序pstest一般在psmatch2后使用,其匹配权重也来自于psmatch2中的_weight.关于匹配权重详情,请见psmatch2的帮助文件.同时,文献中通常会画出匹配前后的倾向得分核概率密度分布图用以支持共同支撑假设(如图1和图2).基于这两步操作,既有文献认为验证了倾向得分匹配的有效性.然而,简单的匹配加权均值差t检验只能反映加权总体控制变量分布平衡性的一个维度,比较片面.而倾向得分概率密度图只是一种简单的图示,可能无法反映变量之间真实的匹配程度.

(a)匹配前

(a)匹配前

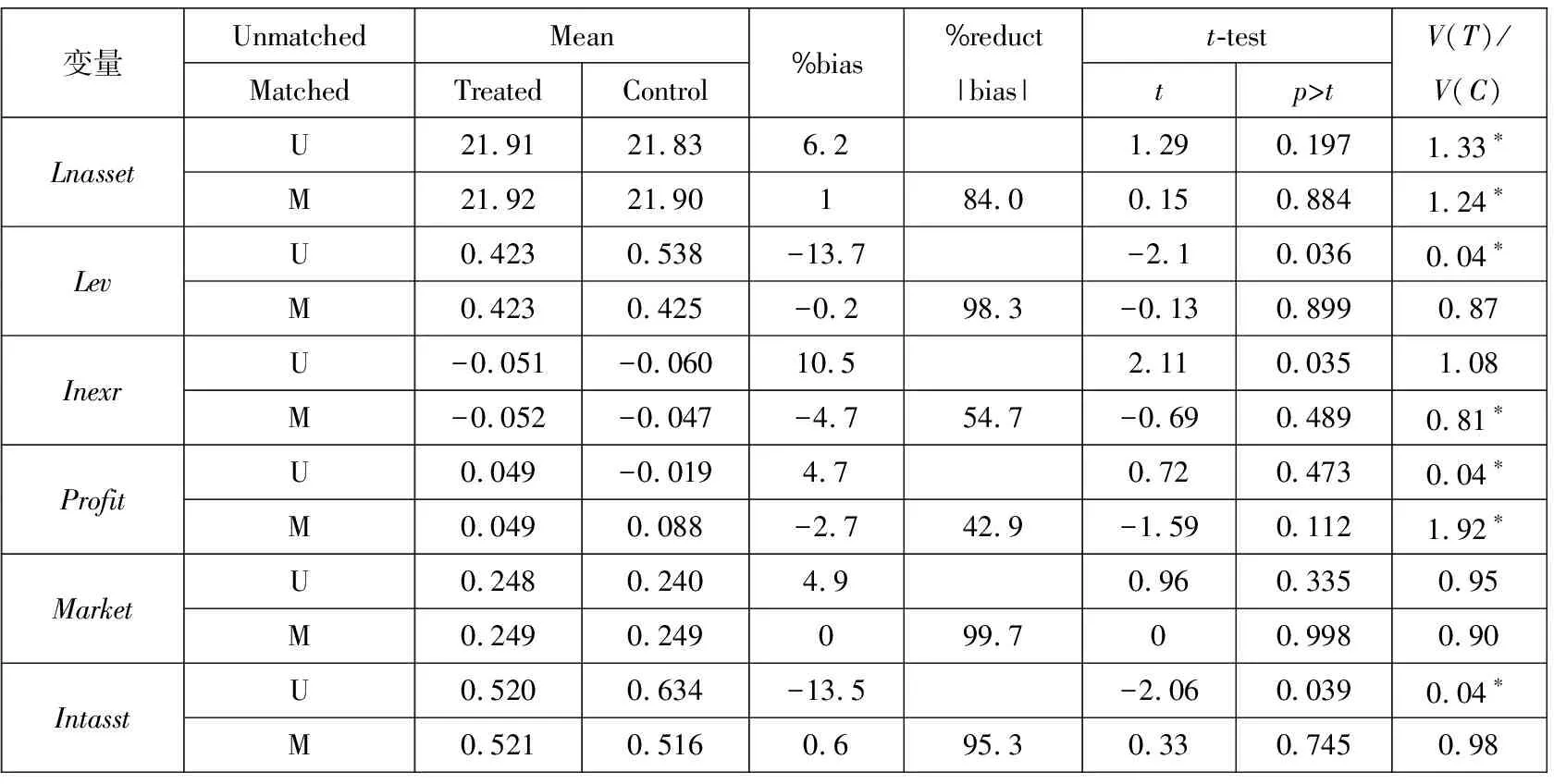
表1 匹配前后平衡性检验结果

1.2 值得关注的多维测度

简单的加权均值差异t检验,只能反映控制变量的均值在处理组和控制组之间有无显著性差异,且由于目标总体会随着匹配权数的选择而改变,容易忽略处理组和控制组样本数量的差异,忽略对处理组控制变量和控制组处理变量的方差、分位数、分布高阶矩等信息的考察.而平衡性要求(关键)控制变量的分布尽可能一致,所以仅仅依靠一种均值检验可能并不能说明平衡性的好坏,更无法判断研究设计的优劣.特别地,在实证研究中,由于倾向得分模型可能被误设,仅依靠倾向得分的平衡性并不足以判断研究设计如“准自然实验”构造的好坏,构造多种多维度的平衡性测度就显得尤为迫切.基于此,本文参考前沿文献[12],推荐以下六种值得关注的控制变量平衡性测度指标:

1.2.1 标准化均值差异

标准化均值差异是指经过处理组和控制组组间标准误标准化后的组间均值差异,具体公式如下

(1)

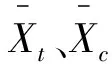
(2)

(3)

使用样本方差的优点是考虑了处理组和控制组之间的样本数量的差异.在大多数政策评价实例中,处理组的个体数量一般远小于控制组的个体数量.文献经验显示,标准化均值差异和平均处理效应(ATE)的估计偏差高度相关,绝对标准化均值差异(即标准化均值差异的绝对值)在百分之十以下才能认为是达到一个比较好的平衡性[22].

1.2.2 马氏距离

马氏距离(Mahalanobis Distance),也称马哈拉诺比斯距离,是一种有效的衡量两个样本相似度的测度.与欧氏距离不同的是它考虑到了各个控制变量之间的联系,并且是尺度独立的(scale-invariant).其表达式为

(4)

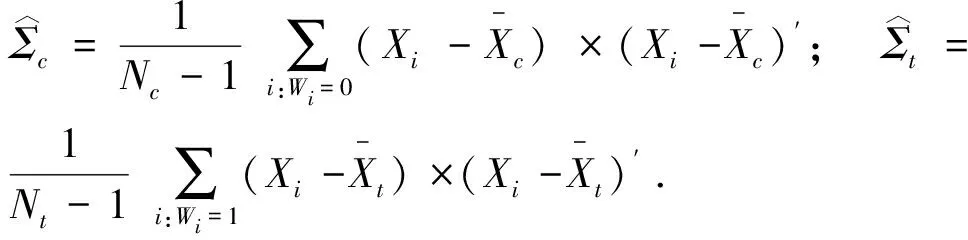
1.2.3 线性化倾向得分的标准化均值差

(5)

1.2.4 对数样本标准误比

对数样本标准误比(Ln Ratio of Standard Deviations),即对处理组与控制组控制变量样本标准误比值取对数,主要反映样本间控制变量的分散程度(spread dispersion)差异.数学表达式为

(6)

其中St、Sc分别为处理组、控制组的样本标准误.对数样本标准误比是一个控制变量分散度的测量,它也是尺度独立的.与简单的样本标准误差值或者样本标准误比值相比,对数样本标准误比值更接近于服从正态分布,便于下一步的判定.

1.2.5 分位数差异

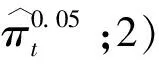
(7)

(8)

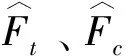
1.2.6qc&qt

与分位数差异类似,另外一种直接的测度就是基于线性化倾向得分的分位数差异qc&qt,用以测量控制组和处理组的共同支撑.若至少能找到一个对照组(i′∶Wi′=1-Wi)中样本和其有接近的线性化倾向得分值,也即线性化倾向得分差异小于一个门槛值lu(通常设为0.1或者0.05),定义二值变量ζi为1,否则为0.具体数学表达式如下

(9)

基于此,qc&qt具体表达式为

(10)

(11)

其中Nt是处理组样本数,Nc是控制组样本数,qc和qt反映的是控制组(和处理组)中能找到参照组中类似个体的样本数占该组总样本的比例.

总体上来看,以上推荐的六种测度中,测度(1)、测度(2)和测度(5)是针对每一个控制变量的度量;测度(3)、测度(4)和测度(6)是针对所有控制变量的多维平衡性测度.测度(1)～测度(4)是标准化距离的度量,测度(5)～测度(6)是控制组和处理组分位数差异的度量.这些测度方法更注重控制组和处理组整体分布的平衡性,比传统的(加权)均值t检验更加全面与客观.但是,要求所提出的六种平衡性检验全部满足在观测数据实证分析中难以实现,研究者可以根据样本量和研究需要,尽可能满足多种平衡性指标,如Imbens[22]和 Athey 和 Imbens[23]推荐至少满足标准化均值差异、对数样本标准误和分位数差异这三种指标.

2 实例分析: PSM-DID

通过两个实例来说明本文推荐的多种平衡性测度的有效性和实用性.

2.1 “营改增”试点对制造业经营多元化的影响

2.1.1 政策背景

为克服传统税制重复征税的缺陷[24],国务院批准自2012 年1月1日起,率先在上海实施了交通运输业和部分现代服务业营改增试点.在原有17% 和13%两档增值税税率下,新增了11% 和6%两档较低税率.在上海试点的基础上,2012年9月1日～2012年12月1日,“营改增”试点扩大至北京市、天津市、江苏省、安徽省、浙江省、福建省、湖北省与广东省8 个省份.一年后,“1+6”行业“营改增”推广至全国所有地区.并逐步推广至全国和其他服务部门.下面将基于我国“营改增”税制试点政策这一“准自然实验”,将2012年进行试点的上海市制造业上市公司作为处理组,使用PSM方法匹配其他未进行“1+6”行业“营改增”试点省份的制造企业作为控制组,探究税制改革对制造业经营多元化的影响.

2.1.2 数据与模型

1)数据来源

数据来源Wind数据库,使用2008年—2014年全部制造业行业的上市公司相关数据.从收集的数据中可以看出,非试点省份中有3 288个上市制造业公司观测值,政策处理节点2012年以前观测值1 794个,2012年以后1 494个;处理组(上海市)有475个上市制造业公司观测值,其中政策时间节点2012年以前观测值259个,2012年后216个.

2)实证模型

采用双重差分方法来估计“营改增”试点政策的因果效应,并应用倾向得分匹配(PSM)来构造可比较的处理组和控制组,即在上海的制造业上市公司和非试点省份的上市制造业公司,减少由于样本选择所带来的内生性风险.具体而言,使用的模型如下

PilotVATi=α0+α1Lnassetit+α2Inexrit+

α3Levit+α4Profitit+

α5Marketit+α6Intassetit+εi

(12)

Revstruraipt=β0+β1Treatp×Postt+

β2Xipt+ηi+γt+ζit

(13)

其中,下表i,p,t分别表示企业,省份和年份.具体地,方程(12)为估计倾向得分的选择方程(Selection Equation),是用于PSM匹配的Pooling Logit回归模型,被解释变量PilotVATi为是否加入政策试点的虚拟变量.若企业i位于“营改增”政策试点地区则为1,否则为0.参照已有文献[25],本文匹配变量选择了可能影响“营改增”试点地区选择的企业特征变量:Lnasset(对数资产总额),Inexr(投资支出比,用于购建固定资产、无形资产以及其他长期资产支付的现金与总资产之比),Lev(资产负债率,为企业年末负债总额与资产总额之比),Profit(利润率,营业利润与营业收入之比),Market(市场势力,用勒纳指数衡量,指产品价格与边际成本间的差额,本文采用主营业务收入减主营业务成本之差除以主营业务收入之比获得),Intasset(无形资产占比,企业的无形资产总额与总资产之比).

方程(13)是评估政策的结果方程(Outcome Equation),是一个双重差分模型.其中选取Revstrura(主营构成第一名在营业收入中占比)为因变量,反映制造业公司的营业集中度.Treat为政策试点地区的虚拟变量,如果制造业上市公司所在地为上海则Treat为1,否则Treat为0;Post为政策实施年份前后的虚拟变量,2012年以前年份为0,2012年及以后为1.因此,双重差分交互项Treat×Post前的系数为双重差分估计的“营改增”对试点地区制造业上市公司的净效应.Xipt为控制变量,即方程(12)中的6个企业特征(Lnasset、Inexr、Lev、Profit、Market、Intasset).在结果方程中,本文控制了公司层面个体固定效应ηi和年份固定效应γt.

2.1.3 倾向得分匹配结果

如前所述,本文先进行倾向得分匹配,在估计完倾向得分值之后,常用的匹配方法有以下几种:1)有放回的最近临近匹配,通常选择1∶4[26]或者1∶1(最优的情况,但是会损失一定样本)同时限制最大卡尺(Caliper)距离为0.05; 2)半径匹配,即选择一个倾向得分匹配所能允许的最大半径值,可以选择0.05或者选择一个倾向得分的标准误;3)核加权匹配,需要选择一个匹配的核函数,一般选高斯核函数(Gaussian)或者双权重核函数(Biweight).本文选择文献中常用的1∶1临近匹配方法(用psmatch2实现).(4)考虑到估计的倾向得分所带来的不确定性,1∶1近邻匹配严格意义上应该使用teffect psmatch程序包,但是使用teffect psmatch时无法获得控制变量的回归系数及显著性。鉴于此,本文采用了文献中常用的psmatch2程序包中1∶1匹配方法,得到基于均值平衡性检验表及倾向得分重合度检验图,并加上共同支撑假设进行样本删减,以便进行后续回归分析.匹配前后控制变量的均值差异如表1所示.

表1中第二列为匹配前后标识变量,U代表未匹配(Unmatched),M代表匹配后(Matched).第三列、第四列为匹配权重加权后的均值,第三列为处理组均值,第四列为控制组均值.第五列%bias是标准化平均值差异.公式为(Weighted Mean_T-Weighted Mean_UT)/SD,即用表格中处理组与控制组的加权均值之差,除以该变量加权样本的标准误.(5)这里的加权样本标准误为控制组和处理组加权样本方差的均值开根号,详见Stata软件中pstest帮助文件.第六列%reduct |bias|是匹配后标准化平均值差异下降的幅度,其数值是通过前面 %bias一列得到的,公式为(| UnMatched %bias |-|Matched % bias | ) / |UM%bias|,度量匹配之后处理组和控制组间的bias减少了多少.第七列、第八列的t-test,用于判断前述的 %bias 是否显著,若显著则说明针对该变量而言,处理组和控制组的加权均值差异是显著的.最后一列V(T)/V(C)为控制变量方差比.星号表示控制变量方差比值超过F统计量2.5%和97.5%分位值,表示值得关注的控制变量,详见Austin[27].

从上表中可以看出匹配完后的样本,加权均值差异的t检验都通过,加权均值差异在统计意义上都不显著,但是方差比值(Varianceratio:=V(T)/V(C))仍然比较显著,如Lnasset,Inexr,Profit,而且加权总体可能并不是政策研究所关注的总体.然而,在实证中这些通常被忽略.本文将在平衡性检验中使用更多的直观测度来检验控制变量的平衡性.

图1展示了匹配前后控制组和处理组倾向得分的核密度分布图.图1(a)中匹配前处理组的倾向得分分布和控制组的并不完全重合(特别是众数明显不一致),且有一些倾向得分较小或者较大的个体无法找到匹配个体(匹配奇异值).但是匹配后,从图1(b)中可以看出处理组的倾向得分分布和控制组基本重合(众数和分布区间基本一致),共同支撑假设基本成立.值得注意的是,匹配过程中删掉了36个匹配奇异值.下文实例分析中本文将基于此匹配样本比较常用的PSM-DID估计方法和本文提出的新方法.

2.1.4 平衡性测度

此处将第一章中推荐的六种平衡性测度方法应用到“营改增”的数据中,以期从多方面来衡量控制变量的平衡性,并从不同侧面考察控制组和处理组的可比性.

表2中前4列为控制组均值、控制组标准误、处理组均值和处理组标准误.从表2第5列开始,汇报了四种新的平衡性测度:标准化差值、对数标准误比、控制组5%分位点对应值和处理组5%分位点对应值.从表中可以发现,通过倾向得分匹配后,处理组与控制组均值和标准误都比较接近,但是从新的测度指标发现,有些变量并没有如预期的那样完全平衡.例如,对数资产总额lnasset标准化差值和处理组5%分位点对应值都比较高,说明控制组在2.5%分位数以下及97.5%分位数以上的制造业上市企业很难找到与其匹配的处理组;资产负债率Lev对数标准误比较大,说明尽管处理组和控制组均值接近,但是分布比较不均;利润率Profit和无形资产占比Intasst也存在类似的问题;最后,本文发现即使将所有控制变量单一化为倾向得分,估计的倾向得分在处理组5%分位点对应值为0.098,表明控制组的倾向得分在2.5%分位数以下及97.5%分位数以上的制造业上市企业很难找到与其匹配的处理组.(6)这对于估计ATT来说问题不大,但是对估计ATE或者ATUT来说会产生一些偏误.这从侧面反映匹配后的样本也存在一定程度的不平衡性.如果在实际测算中发现其值偏离0.05较多,则可依据更严格标准进行匹配或者加权.

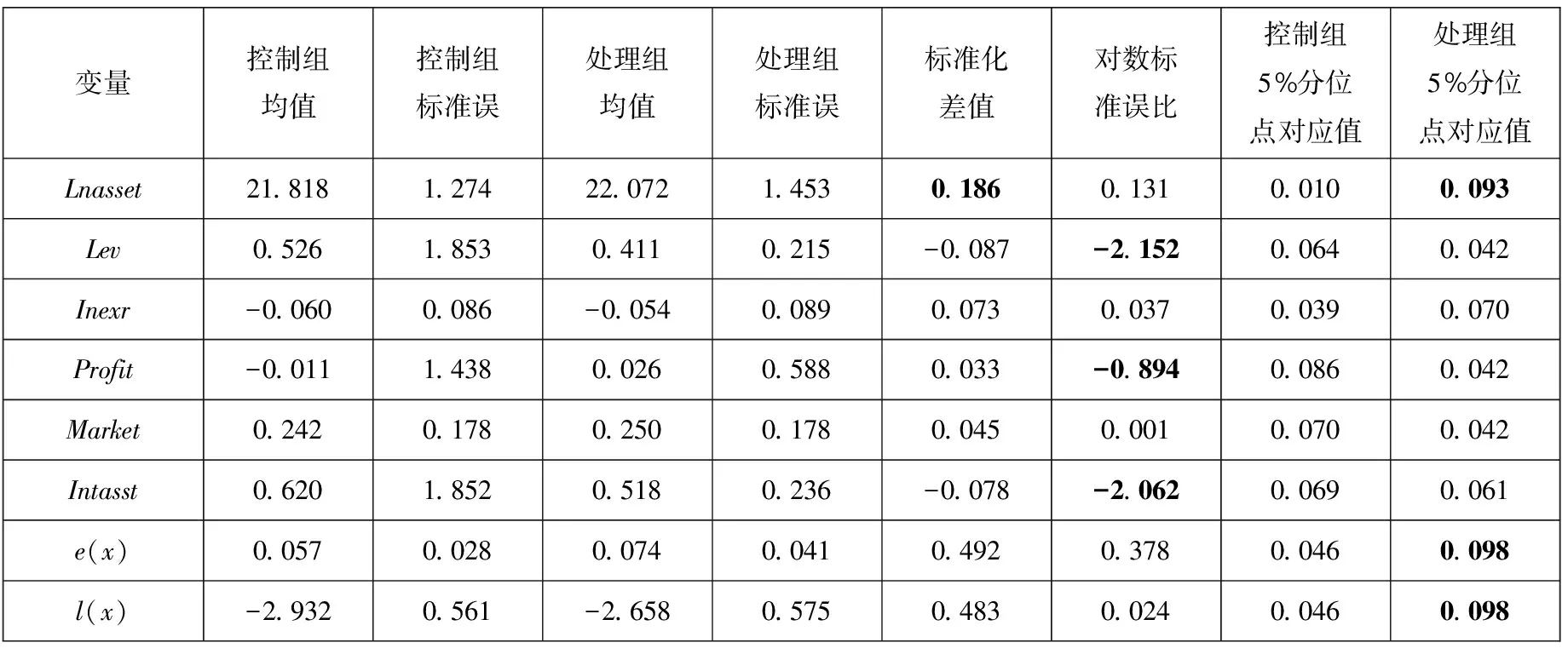
表2 多维度平衡性检验

本文还计算了其他两种平衡性的测度:Mahalanobis得分和qc&qt.计算得到的Mahalanobis得分是0.292 1,大于经验值0.1.当固定最大倾向得分间距为0.1时,得到qt=0.981,qc=0.979,即有1.9%的处理组个体找不到匹配的控制组个体,有2.1%的控制组个体找不到匹配的处理组的个体.这些都从不同侧面说明倾向得分匹配后样本的平衡性还有进一步提高的空间或者模型还有待进一步改进.

2.2 智慧城市试点对城市PM2.5排放量的影响

2.2.1 政策背景

2010年开始,中央及地方政府就分别从顶层设计到具体应用不断推出指导和鼓励智慧城市建设的相关政策.2012 年 12 月 5 日正式发布“关于开展国家智慧城市试点工作的通知”,并印发《国家智慧城市试点暂行管理办法》和《国家智慧城市(区、镇)试点指标体系(试行)》.首批国家智慧城市试点共涉及 90 个地、县级城市.本小节将基于我国首批智慧城市试点政策这一“准自然实验”,以首批试点城市作为处理组,采用PSM方法选择合适的非试点城市作为对照组,考察智慧城市试点对空气污染物PM2.5排放量的影响,从侧面检验数字化发展对环境保护的影响.

2.2.2 数据与模型

1)数据来源

PM2.5数据来自于哥伦比亚大学国际地球科学信息网络中心(CIESIN)所属的社会经济数据和应用中心(SEDAC)公布的相关数据.城市层面控制变量数据来自 2006年—2016 年《中国城市统计年鉴》.智慧城市名单来自住建部公布名单,将其与中国城市统计年鉴、PM2.5数据匹配,最终得到 2005年—2016 年中国 278个地级市 12年的面板数据3 332个样本.

2)实证模型

为探究智慧城市试点对城市PM2.5排放的影响,使用PSM-DID,基于具有可比性的处理组和控制组分析被处理城市的平均处理效应(ATT),减少由于样本自选择所带来的内生性风险.具体来讲,以省内试点城市为处理组,以省内非试点城市为对照组,构建模型如下

Smart_Cityc=α0+α1Popct+α3Economicct+

α4Financect+α5Urbanct+

α6Openct+εc

(14)

PM2.5ct=β0+β1TreatC×Postt+

β2Xct+δc+γt+ζit

(15)

其中,方程(14)为估计倾向得分的选择方程(Selection Equation),采用logit回归模型,被解释变量Smart_CityC为是否加入政策试点的虚拟变量:若城市c为试点城市则为1,否则为0.参考既有文献[28],本文控制了以下城市特征变量(Xct):人口规模(Pop),计算方式为ln(年末总人口);经济发展水平(Economic),计算方式为ln(人均地区生产总值);金融发展水平(Finance),计算方式为ln(年末金融机构人民币各项贷款余额);城市化水平(Urban),计算方式为100×非农业人口/年末总人口;市对外开放程度(Open),计算方式为外商实际投资额/地区生产总值.

方程(15)为评估政策的结果方程(Outcome Equation),基于匹配后样本进行双重差分回归.被解释变量为城市年平均PM2.5.TreatC为智慧城市二值变量:若为智慧城市试点城市,则为1,反之则为0.Postt为政策前后虚拟变量,若年份大于2011年,则为1,反之为0.因此,核心解释变量为双重差分交互项TreatC×Postt.Xct为城市层面控制变量.δc为城市层面固定效应,控制了不随时间变化的城市特征.γt为年份固定效应,控制了宏观趋势对回归结果的影响.

2.2.3 倾向得分匹配结果

由表3,对比倾向得分匹配完后的各变量的加权样本均值,实验组和对照组的均值差异在统计意义上都不显著(p值都大于0.1),因此若按照文献中广泛使用的简单比较均值差异将得出匹配后样本满足平衡性假定的结论.但是仅从表中信息看,城市化变量方差比值(Varianceratio:=V(T)/V(C))部分显著,显示出两组分布的非均衡性,然而在实证中方差比值通常被忽略.后文将在平衡性检测中使用更多的测度来检验控制变量的平衡性.

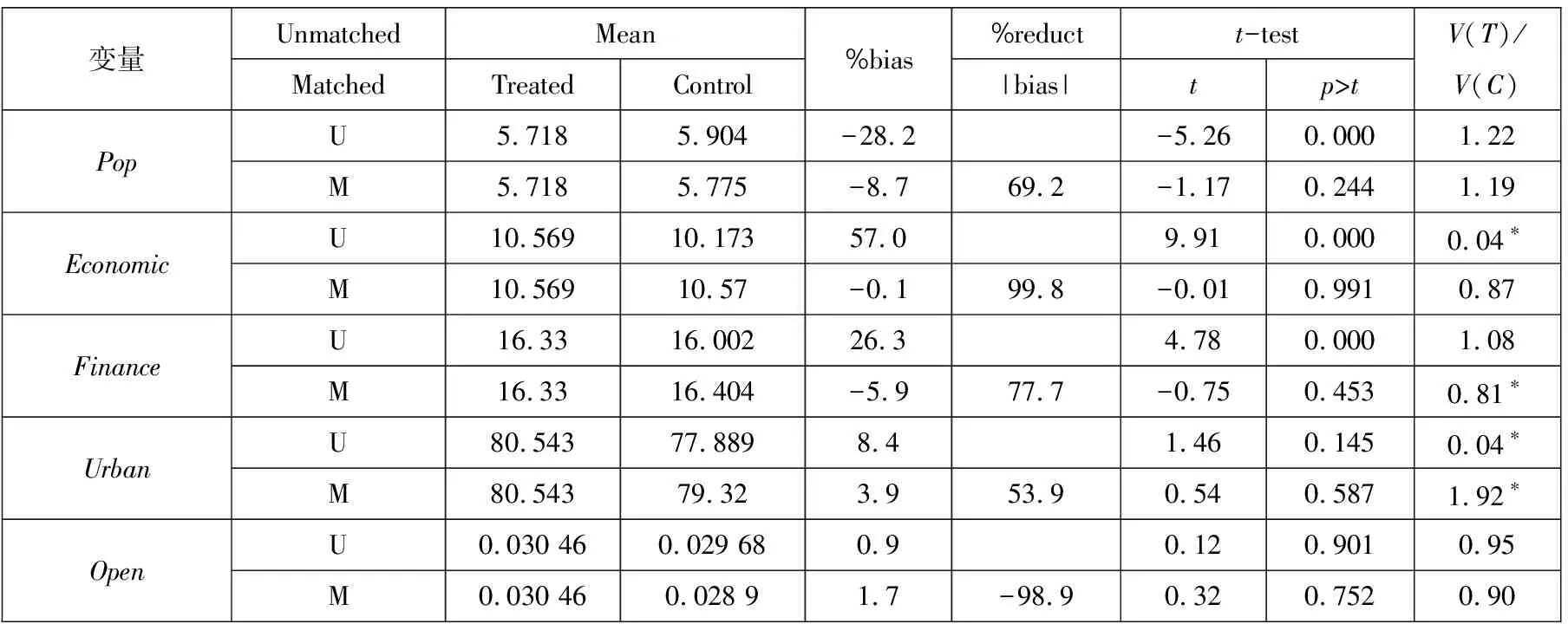
表3 匹配前后平衡性检验结果

更进一步,图2展示的是匹配前后控制组和处理组倾向得分的核密度分布图.图2(a)中匹配前处理组的倾向得分分布和控制组的并非完全重合,众数和均值表现出明显不一致,且存在匹配奇异值(Outlier),有一些倾向得分较小或者较大的个体无法找到匹配个体.但是匹配后,从图2(b)中可以看出处理组的倾向得分分布和控制组基本重合,众数和分布区间基本一致.值得注意的是,匹配过程中删掉了255个的匹配奇异值.类似地,在后文将基于此匹配样本对常用的PSM-DID估计方法与本文提出的新方法进行比较.

2.2.4 平衡性测度

在此将第一章中推荐的六种平衡性测度方法应用到本案例中,以期从多方面来衡量控制变量的平衡性,也从侧面考察控制组和处理组的可比性.

表4中前4列为控制组均值、控制组标准误、处理组均值和处理组标准误.从第5列开始,汇报了四种新的平衡性测度:标准化差值、对数标准误比、控制组5%分位点对应值和处理组5%分位点对应值.表4显示,经过倾向得分匹配后,处理组与控制组的均值和标准误都比较接近,然而考察新的测度发现,部分变量并未实现完全平衡.例如,除对外开放水平外,其余控制变量的标准化差值都较高,说明尽管处理组和控制组均值接近,但是分布比较不均.城市化、对外开放水平的对数标准误差比也都较高.经济发展水平、金融发展、城市化水平控制组5%分位点对应值都比较高,说明处理组的2.5%分位数以下与97.5%分位数以上的城市很难找到与其匹配的控制组.人口规模、经济发展水平处理组5%分位点对应值都比较高,说明控制组的2.5%分位数以下与97.5%分位数以上的制造业上市企业很难找到与其匹配的处理组.最后,表中结果显示即使将所有控制变量单一化为倾向得分,估计的倾向得分在控制组和处理组5%分位点对应值都较大(相对于理想情况0.05而言),说明处理组和控制组的倾向得分都在2.5%分位数以下与97.5%分位数以上的制造业上市企业很难找到与其匹配的处理组.

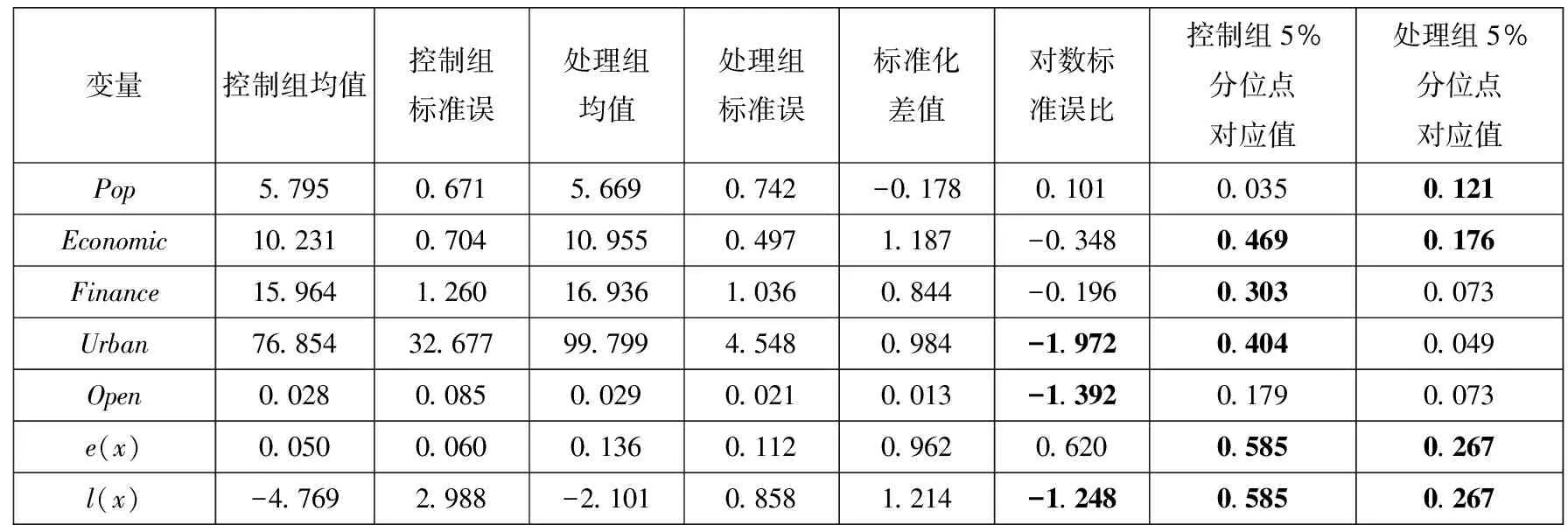
表4 多维度平衡性检验

本案例仍计算了其他两种平衡性的测度:Mahalanobis得分和qc&qt.计算得到的Mahalanobis得分是1.108,远高于经验值0.1.当最大倾向得分间距固定为0.1时,qt=0.988,qc=0.546,即有1.12%的处理组未能与控制组匹配,而有45.4%的控制组个体未能与处理组匹配,进一步说明了控制组与处理组之间样本的不平衡性.以上案例分析结论进一步验证了仅考察均值差异的片面性和误导性,显示出采用更为全面的平衡性测度指标的重要性和必要性.

3 改进的方法: PSM-IPW-DID

3.1 改进方法

通过前面的实例可以看出,仅仅只对均值差异(Mean Difference)做t检验只是一种方便性的选择,远不足以验证控制变量的(分布)平衡性.对于平衡性的检验,研究者需要从多个角度多个维度来衡量,例如本文推荐的标准化均值差,分位数测度和离算程度差异等等.但是由于研究中通常使用观测数据,使用多个平衡性测度后常常会发现有些控制变量不能完全平衡甚至分布相差很大,随之而来的问题就是:怎样提升平衡性呢?怎样提升所估计因果效应(Causal Effect)的可靠性呢?

在引入多种平衡性测度后,可能会出现PSM很难满足(绝对的)控制变量平衡性.为了达到更好的平衡性,一种直接的方法是使用严格的匹配的标准(Criterion),但是这样不仅会使得样本量大量减少,还可能导致后续的双重差分估计结果不显著.样本量的减少会使得估计结果没有代表性,双重差分结果不显著表明政策效应无法被干净的识别和估计.

为了克服以上问题,本文提出了一种倾向得分匹配-逆概率加权-双重差分(PSM-IPW-DID)的方法.逆概率加权(IPW)由Horvitz 和 Thompson[29]提出来(HT估计量),随后被计量经济学家广泛引用,如Hahn[30]、Hirano等[31]、Frölich[16]、 Huber 等[17]、Busso 等[18]等等.类似地,文献中用逆倾向得分概率加权来计算处理组和控制组的样本均值,这样能有效地去除处理组和控制组由于控制变量的不平衡性和差异性所带来的处理效应估计误差.具体来讲,在非混淆假设(Confoundedness)下,利用重复期望法则能得到

(16)

(17)

基于此,两个直接样本的估计量为

(18)

(19)

因此,所感兴趣的平均处理效应估计量(也是一个HT估计量)可写为

(20)

在实际操作中,可对逆倾向得分权重进行标准化处理,使得其加总和为1

(21)

(22)

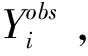
(23)

这是一种双重稳健(Double Robust)的分析,详见Sloczynski 和 Wooldridge[32].具体体现在

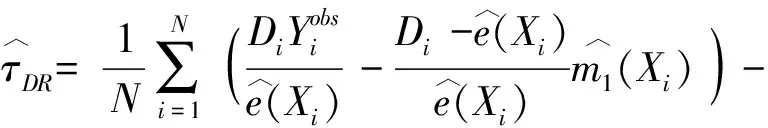
(24)

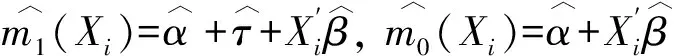
(25)

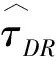
3.2 估计步骤

本质上,本文提出的方法结合了倾向得分匹配和逆概率加权的长处,规避了二者短处,得到了一种更为稳健的估计方法.倾向得分匹配会删除掉一些样本来增加控制变量的平衡性(从而克服样本自选择带来的内生性)和满足共同支撑(common support)的假设,而逆概率加权则可以在不减少样本的情况下控制变量的不平衡性,基于(已匹配)样本还原总体,通过概率加权的方法使得控制组和处理组更加可比,估计结果更有效.倾向得分匹配和逆概率加权的结合使用既能克服控制变量的不平衡性又能减少删除样本数量,而且克服了单独使用倾向得分匹配(PSM)不足以平衡所有控制变量的短板,也规避了单独使用逆概率加权(IPW)出现极端概率导致估计值方差过大的风险.具体来讲,本文提出以下估计方法:

第二步,运用本文提出的多种平衡性测度衡量控制变量的平衡性,选出需要特别关注的不能平衡的控制变量Xub(控制变量X的一个子集);(7)对于这些通过PSM不能平衡的控制变量,需要将其加入到后续的DID回归中,甚至考虑其高阶形式.为了方便起见,后续实例研究中,本文只比较了不加入控制变量和加入所有控制变量两种情况.

第四步,基于匹配后的样本S和得到的逆概率加权,进行包含控制变量X(包含Xub)的加权双重差分回归,如下所示

Yit=α0+α1Treat+α2Post+α3Treat×

Post+Xit’β+εit

(26)

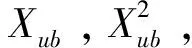
值得注意的是,本文提出的PSM-IPW也可应用于直接估计ATT的(均值相减)模型估计中.如引言中所述,在近十年发表在经济学管理学主要期刊上的169篇使用倾向得分匹配的论文中,62篇是将倾向得分匹配直接应用于均值相减的处理效应ATT估计中.对于这些实例,本文提出的方法只需将第四步的估计方法中双重差分模型改为一个加权均值相减模型使用加权最小二乘法(Weighted OLS)即可.

本文提出的方法既使用了逆概率加权,也加入了(不平衡的)控制变量进行回归,得到的估计量是一个逆概率加权-回归调整的估计量(IPWRA,详见Wooldridge[20]).如上文所述,在处理选择模型设定有误而回归模型是正确时,逆概率加权不会影响包含控制变量调整的回归模型分析;另一方面如果处理选择模型设定正确而回归模型有误时,逆概率加权可以纠正回归模型,得到一致性的估计值.从这个意义上来讲,该估计量沿袭了逆倾向得分加权回归的优点,具有双重稳健的性质(double robustness)[12].

同时,和其他DID的改进方法如Abadie[33]和Sant’Anna等[34]类似,本文提出的改进方法适用于面板数据,也适用于重复横截面数据(repeated cross sectional data).基于DID设计,在处理重复横截面数据时,需要构造一个“伪”面板数据(psudo panel data).如果不考虑DID设计,本文提出的加权方法也适用于截面数据,如文献中Soczyński等[35]文章中提出的在截面数据中适用的类似方法.具体来讲,首先估计倾向得分,以处理组为基础,通过倾向得分来匹配控制组样本,然后构造逆倾向得分权重(IPW),通过加权最小二乘回归(OLS)估计处理组的平均处理效应,即ATT.

3.3 数值模拟

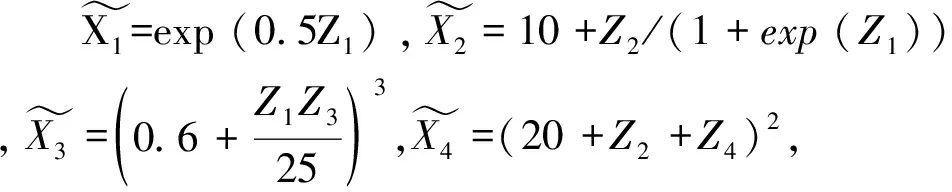
与Kang和Schafer[36]和Sant’Anna等[34]等文献类似,本文考虑以下四种数据生成过程(data generating process)

DGP1:Y0(0)=freg(X)+v(X,D)+ε0,

Y1(d)=2freg(X)+v(X,D)+ε1(d),d=0,1

D=1{p(X)≥U}

DGP2:Y0(0)=freg(X)+v(X,D)+ε0,

Y1(d)=2freg(X)+v(X,D)+ε1(d),d=0,1

D=1{p(Z)≥U}

DGP3:Y0(0)=freg(Z)+v(Z,D)+ε0,

Y1(d)=2freg(Z)+v(Z,D)+ε1(d),d=0,1

D=1{p(X)≥U}

DGP4:Y0(0)=freg(Z)+v(Z,D)+ε0,

Y1(d)=2freg(Z)+v(Z,D)+ε1(d),d=0,1

D=1{p(Z)≥U}

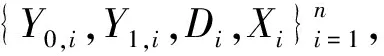
由于本文关注于所观测到的控制变量X线性加入到回归模型和logit倾向得分模型中的情景,因此DGP1中回归模型和倾向得分方程都正确设定,DGP2中只有回归模型是正确设定的,DGP3中只有倾向得分方程是正确设定的,DGP4中回归模型和倾向得分方程设定都不正确.蒙特卡洛数值模拟的结果如表5中所示.

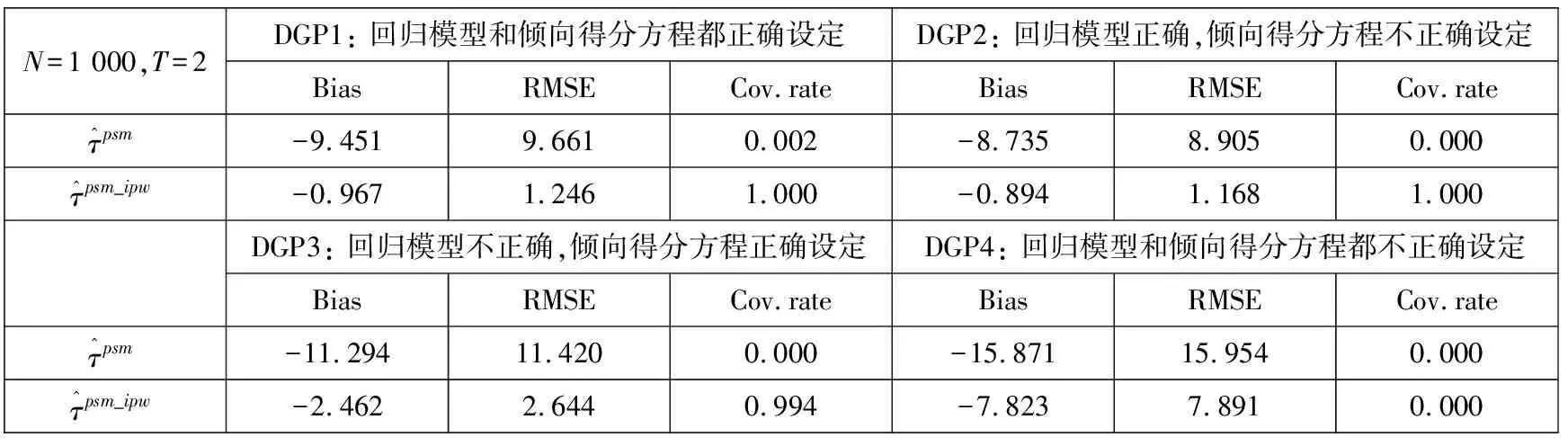
表5 PSM-IPW-DID与PSM-DID估计值数值模拟分析

DGP2a:Y0(0)=frega(X)+va(X,D)+ε0,

Y1(d)=2frega(X)+va(X,D)+ε1(d),

d=0, 1

D=1{p(Z)≥U}

DGP2b:Y0(0)=fregb(X)+vb(X,D)+ε0,

Y1(d)=2fregb(X)+vb(X,D)+ε1(d),

d=0,1

D=1{p(Z)≥U}

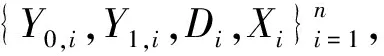
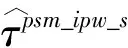
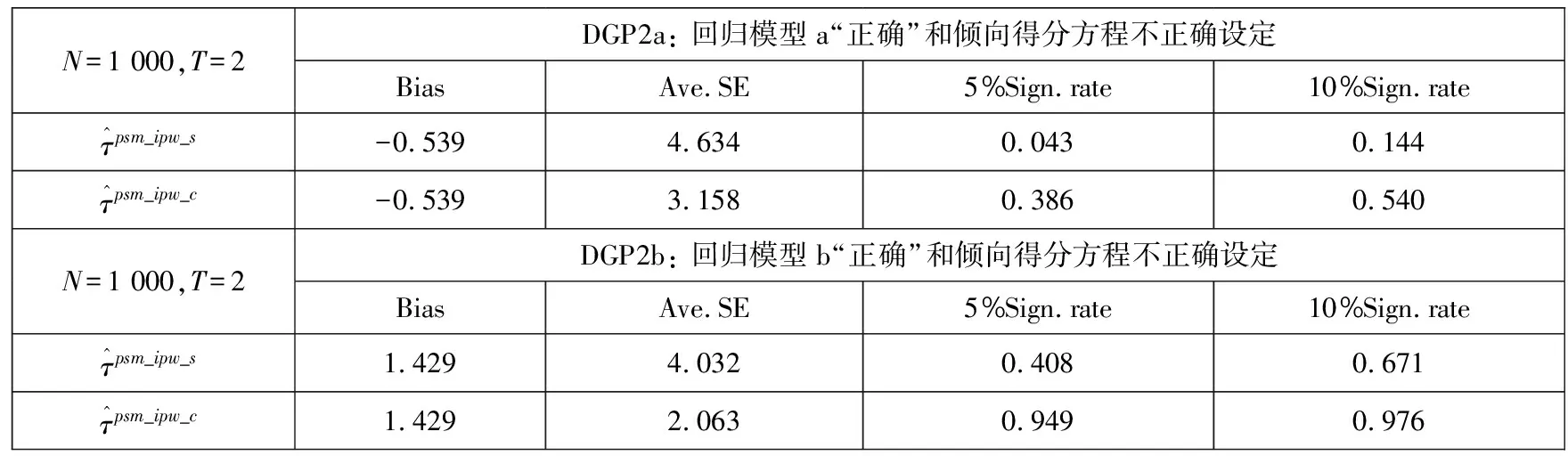
表6 非平衡变量对PSM-IPW-DID估计值影响分析

表6中数值模拟结果显示,控制非平衡变量的高阶项的估计值与只控制非平衡变量的线性项估计值相比,其大小相同且均存在一定偏误,但标准误更小,回归结果更显著.更小的标准误使得了无论是在5%还是10%显著性水平上,控制非平衡变量的高阶项的估计值都更显著.比较两种不同误设程度的回归模型DGP2a和DGP2b,可以发现,误设程度较高的DGP2b模型的估计值偏误较大(|1.429|和|-0.539|),但是一旦控制非平衡变量的高阶项后,标准误就极大降低,而且显著性水平极大提高.这些结论进一步验证了考虑控制非平衡变量的非线性函数关系的重要性,对实证分析也有重要指导意义.

4 实例分析: PSM-IPW-DID

本节将提出的PSM-IPW-DID方法应用于第二章所阐述的两个政策评估实例中,并与文献中常用的PSM-DID方法进行比较.通过实例对比研究,加深对本文所提出方法的理解和应用推广.

4.1 “营改增”实例分析

首先,利用第三节中倾向得分匹配成功并依据共同支撑假设进行删减后的样本进行双重差分估计,结果如下表7中第(1)列、表7第(2)列所示.表7第(1)列中是不包括控制变量的固定效应模型回归结果,表7第(2)列中是包含了控制变量的回归结果.回归结果显示,“营改增”政策对主营构成第一名在营业收入占比有显著的负向作用,其大小为3.4到3.7个百分点.在加入所有企业层面控制变量和企业层面的固定效应后,平均意义上来讲,“营改增”政策减少了试点地区上市制造业公司3.7个百分点的主营构成第一名在营业收入占比,这说明制造业上市公司有分散经营的动向.

表7 “营改增”对营业收入占比的影响

在表7第(3)列和表7第(4)列为使用本文提出的PSM-IPW-DID方法估计的政策处理效应.表7第(3)列中是不包括控制变量的固定效应模型回归结果,表7第(4)列中是包含了控制变量的回归结果.具体地,表7第(4)列加入了所有控制变量以及表2中非平衡变量Lev,Profit,Intasst的二次项,即Lev2,Profit2和Intasst2.回归结果显示,“营改增”政策对主营构成第一名在营业收入占比有显著的负向作用,其大小为4.1到4.3个百分点.在加入所有企业控制变量和企业层面的固定效应后,平均意义上来讲,“营改增”政策减少了试点地区上市制造业公司4.3个百分点的主营构成第一名在营业收入占比,这说明制造业上市公司经营更为多元化.

值得注意的是,表7中第(4)列是考虑了企业个体固定效应且加控制变量的IPW双重差分模型,与表7第(2)列相比,控制变量的显著性明显降低(表7第(2)列中有三个在1%的显著性上显著,表7第(4)列中只有一个在1%的显著性上显著).控制变量的显著性大幅减少能有效缓解由于双重差分模型误设所导致的估计偏误.这些都从实证上验证了本文所提出来的PSM-IPW-DID比PSM-DID更加稳健.

4.2 “智慧城市”实例分析

类似地,首先,利用倾向得分匹配成功的样本进行双重差分估计,结果如表8中第(1)列、表8第(2)列所示.表8中第(1)列、表8第(2)列为使用固定效应方法进行面板数据回归的结果,其中表8第(1)列未控制城市层面控制变量,仅控制了年份固定效应和城市固定效应,表8第(2)列在其基础上加入了城市控制变量.尽管表8第(1)列回归结果仍然显示该政策对城市PM2.5没有显著影响,但表8第(2)列为最为严格控制的模型,其回归结果显示相比非试点城市,试点城市的PM2.5显著降低0.904,所有城市PM2.5的均值为36.68,因此平均而言,城市的PM2.5显著降低2.5%.

表8 “智慧城市”对PM2.5的影响

随后,将本文提出的PSM-IPW-DID的方法应用在上述的“智慧城市”数据上,得到的结果如表8中第(3)列、表8第(4)列所示.表8第(3)列未加入城市层面控制变量,仅控制了年份固定效应和城市固定效应,表8第(4)列在其基础上加入了城市控制变量,并加入表2中非平衡变量Economic,Finance,Urban的二次项,即Economic2,Finance2和Urban2.回归结果显示,采用改进后的PSM-IPW-DID方法后,智慧城市试点政策对城市PM2.5的排放量没有显著的影响,表明原PSM-DID方法简单平衡性测度错误判断了匹配前后样本的平衡性,从而导致了估计结果并非真实的因果效应,呈现出了虚假的统计显著性,得出了智慧城市对城市PM2.5有显著降低作用的错误结果.

值得注意的是,表8中第(4)列加入控制变量和非平衡变量二次项的IPW双重差分模型与表8第(2)列传统双重差分模型相比,控制变量的显著性减少了一半(粗略比较,表8第(2)列有4个显著,表8第(4)列只有2个显著,且前者显著性明显高于后者),与表8第(3)列不加控制变量的IPW双重差分模型相比DID系数更加接近(-0.678和-0.332).控制变量的显著性大幅减少能有效缓解由于双重差分模型误设所导致的估计偏误.因此,本案例在城市层面的分析也验证了本文提出的PSM-IPW-DID比PSM-DID更加稳健,PSM-DID现有平衡性测度导致样本非均衡时可能呈现出虚假显著性的回归结果.

5 结束语

本文基于文献中常用的PSM-DID估计方法及其平衡性检验的不足,提出了多种平衡性测度方法,并在此基础上提出了一种更加稳健性的PSM-IPW-DID方法.在具体分析中,本文基于文献中研究较多的“营改增”及“智慧城市”的政策评价分析进行探讨,以期能提供更多可操作性的指引和建议.总结下来,本文建议: 1)选择合适的倾向得分匹配方法,如1∶4近邻匹配、半径匹配或者核匹配,以确保匹配后不丢失过多样本; 2)在进行倾向得分匹配后需要选用多种平衡性测度来检验控制变量的平衡性,简单的均值差异t检验是不全面的,本文推荐使用多种多维度平衡性测度; 3)如果发现平衡性无法满足,建议采用本文所提出的PSM-IPW-DID方法进行估计,以期在不进一步损失样本情况下得到更加稳健的估计结果.

本文关注的平衡性测度问题是在倾向得分匹配之后进行的.在未来的研究中,研究者可以关注于倾向得分匹配的具体匹配操作,如基于横截面估计的倾向得分在面板结构的数据如何进行精准匹配(Matching),最新的研究如谢申详等[37]就探讨了该类问题.另外,倾向得分在固定效应模型(不仅仅是双重差分模型)中的应用也是一个值得深入探讨和研究的领域,如Arkhangelsky和Imben[21].以上有益的尝试为未来倾向得分匹配方法的研究提供了新的视角和方向.