三维激光扫描技术与传统测绘技术的精度分析
2024-04-10李鸿奎李静孔维枢
李鸿奎 李静 孔维枢
(1.大连市自然资源事务服务中心,辽宁 大连 116011;2.解放军32023 部队,辽宁 大连 116023)
传统测绘技术,比如全站仪测绘、GPS 测绘等,是对地物完成单点测量,得到测量数据点的坐标信息[1],需要技术人员深入测区,不仅测量速度慢、劳动强度大,在地形复杂区域还存在人员安全隐患[2]。三维激光扫描技术是将实体信息迅速扫描为点云数据,使其变换为电脑可以识别处理的信息,这种信息更加丰富,便于存档[3]。该技术通过高速激光扫描测量,在不直接接触测量物的情况下,快速采集外业数据,获取目标对象表面的三维坐标信息,然后交由内业数据处理。和常规作业方式不同,该技术减少了外业人员的劳动强度,缩小了野外作业的工作周期,自动化程度明显提高[4]。凭借穿透性、高效率、不接触性、实时性强等特点,三维激光扫描技术在军民共建等领域得到广泛应用。
本文利用三维激光扫描技术开展空间数据采集,对获取到的点云数据进行拼接,将不同测站测得的点云坐标统一到同一坐标系下,然后用全站仪对相同地域进行传统数据采集,在两种测量方法的坐标系中找到不少于三对同名点坐标,求解七参数。利用求得的七参数将三维激光扫描仪的点云坐标转换为全站仪的坐标系,最后对数据精度进行对比分析。
1 三维激光扫描技术工作原理
三维激光扫描仪通过发射激光束到物体表面,再经过物体表面的漫反射使一部分激光束返回三维激光扫描仪[5],可计算出扫描仪与被测物体间的距离S。控制编码器同步可测量出激光路径与X 轴的角度观测值,和与Y 轴的角度观测值[6]。X 轴和Y 轴都在横向扫描面且相互垂直,Z 轴则与横向扫描面垂直,计算原理如图1 所示。

图1 地面三维激光扫描仪计算原理
依据图1,可计算出被测物体的三维空间坐标,具体计算公式如下:
公式(1)是以三维激光扫描仪扫描中心为坐标原点,在实际测量工作中需将测量的点云坐标放到实际坐标系统中[7]。
2 三维激光扫描技术在地形测绘中的应用
近年来,三维激光扫描技术发展不断成熟,在建筑物三维建模、水库桥梁变形监测、地籍测绘等领域都得到了普遍应用[8],尤其在地形测绘中,应用三维激光扫描技术,在测定扫描仪测站点定位和后视标靶坐标定向后,获得全景范围内可见面域空间点连续的三维坐标和影像,通过实时设站重新扫描,确保整个测区无遗漏。
获取点云数据后,对数据进行检验并分类处理,经过坐标转换、激光点滤波后,建立测区的DEM 数据,如图2 所示。与传统测绘方法相比,利用三维激光扫描技术获取DEM 数据,操作简单,快速便捷,节省人力物力。

图2 DEM数据
3 实际案例分析
3.1 三维激光扫描仪作业
3.1.1 数据获取
实验使用RIEGL VZ-1000 地面三维激光扫描仪,对道路及两侧地物进行扫描。扫描距离为600m,每秒最高可以发射30 万个激光脉冲,提供高达1.8 秒的角度分辨率。测区道路全长近1.7 公里,由于道路较长,无法一站完成作业,因此实验共设置了9 个测站点。为了便于后期进行数据拼接,相邻测站之间有部分数据重叠。三维激光扫描仪获取的道路点云数据如图3所示。

图3 三维激光扫描仪获取的道路点云数据
3.1.2 点云数据处理
利用三维激光扫描仪对采集的点云数据进行点云拼接,即将不同坐标系下的三维空间数据转换到同一个坐标系[9],将需要拼接的两站数据拖入视窗,点选手动拼接,将基准站放置在A 窗口、拼接站的站点放置在B 窗口,分别在两个窗口数据的共同区域选取四对位置一样的点,具体如图4 所示。

图4 手动拼接
由于三维激光扫描仪采用的是内置坐标系统,要将不同测站测量的数据拼接在同一个坐标系,拼接前后的图像如图5 和图6 所示。

图5 拼接前图像

图6 拼接后图像
3.2 全站仪数据采集
实验使用徕卡高精度全站仪采集数据,该仪器在平均大气条件下测角精度为2",测距精度高;与三维激光扫描仪测点精度相比,单点测量精度较高,且性能较为稳定。
(1)全站仪的布点与测量
在测区找到两个已知控制点K02 与K03,两点相距80 米左右,如图7 所示。在K02 架设全站仪,进行方向定向(即在全站仪中输入当前与后视点坐标),测量道路边界与两侧相关地物。
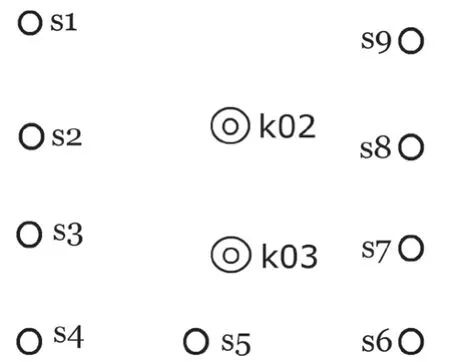
图7 同名点
(2)同名点布设
实验同时使用全站仪与三维激光扫描仪采集外业数据。为了对比两种方法的测量精度,需统一坐标,并以路灯为参照物,在测区布设9 个同名点S1~S9,具体如图7 所示。
3.3 解算七参数
为了将两个不同的坐标系转换到相同坐标系下,首先求出坐标转换所需的七参数,而解算坐标转换的七参数,至少需要三对同名点。这三对同名点要求精度高,分布均匀,并有较大的覆盖面。因此,本次选取S1、S5、S9 三对同名点,七参数结算完成后得到同名点转换前后坐标值,最终求得七参数,结果如表1所示。
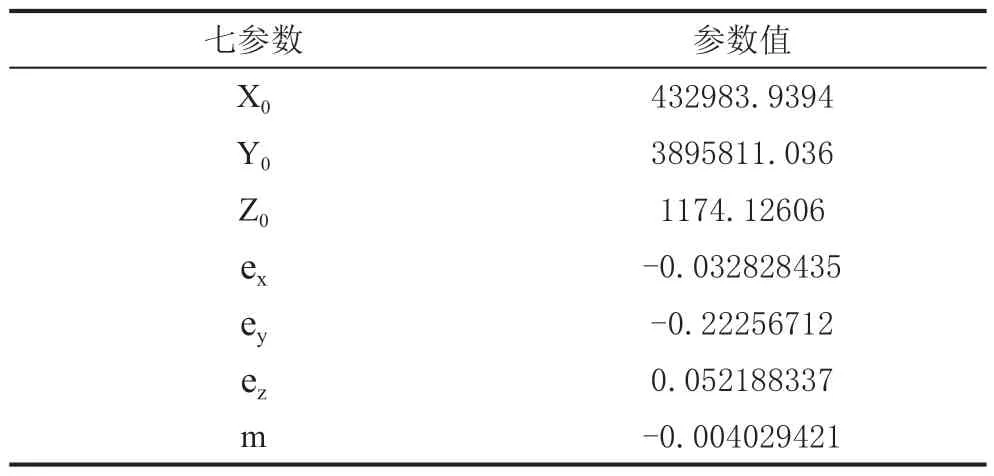
表1 七参数结果
3.4 坐标转换后的点位误差分析
布尔莎模型是一种用于描述地理空间不确定性及其传播机制的概率模型,在测绘领域被广泛用于估计和传播测量误差。实验采用布尔莎模型对特征点进行坐标转换,转换后的坐标与全站仪所测坐标有所不同,具有一定的误差。为了比较转换前后坐标差值的大小,整体评价转换后的点云精度,根据转换后的坐标较差Δx、Δy、Δz,计算三维激光扫描仪不同测站点之间的点位误差,并比较其精度与距离的关系。点位误差公式为:
在测区选取几个不同的点,选点要清晰明确,可在三维激光扫描仪和全站仪两种坐标系下找到对应的坐标值,同时点与点之间的距离尽量保持一致,使各点与三维激光扫描仪尽量在一条直线,如图8 所示。根据公式(2)计算出各点的点位精度值。

图8 与扫描测站不同距离的点
根据布尔莎模型,将D1 至D6 三维激光扫描仪下的坐标转换到全站仪下的坐标,根据公式(2)求出转换后的点位误差,结果如表2 所示,各点的点位误差与距离的趋势如图9 所示。
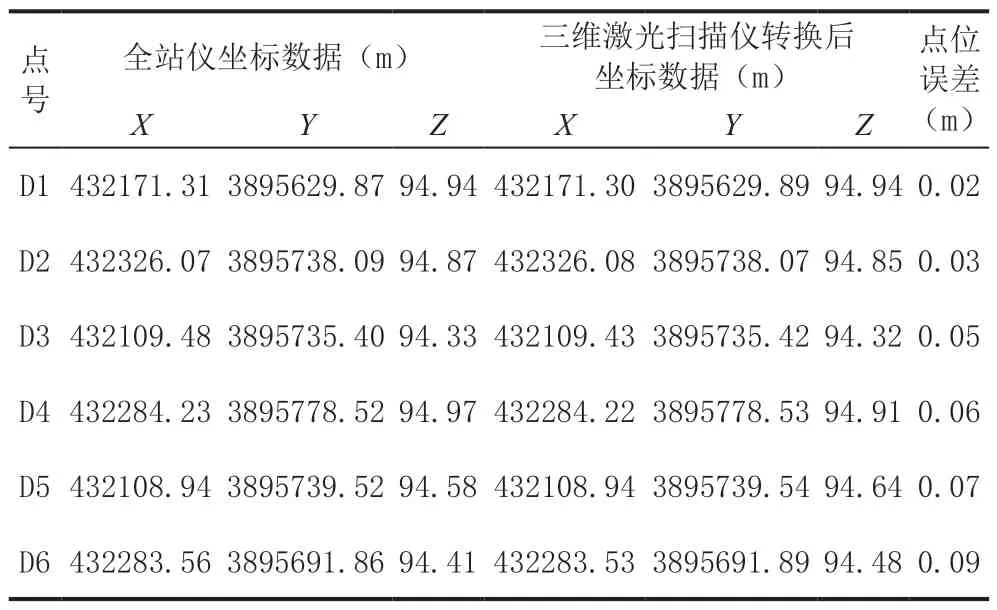
表2 坐标转换后的点位误差

图9 点位误差与距离趋势
通过实验数据与图表分析,可以发现三维激光扫描仪测量点坐标误差与其距离有关,随着距离的增大,误差呈增长趋势。
4 精度分析
实验分别利用全站仪和三维激光扫描技术对参照物进行数据采集。在使用全站仪对测区进行数据采集时,选取该地物边侧三个不同的点位进行观测,读取三个坐标数据,并求出中心点坐标,再根据七参数进行坐标转换,结果如表3 所示。

表3 中心点坐标
根据表3,点号SW 是在三维坐标下获取的路灯中心点,表3 第二行数据是三维激光扫描仪坐标系下的坐标值,第三行是经过坐标转换后相对应的坐标值。求出路灯边侧三个点与中心点的坐标值,如表4 所示,J128 至J130 是三个边侧点,ZD 是其中心点坐标,分别求出SW 与其余四个点的点位误差值。
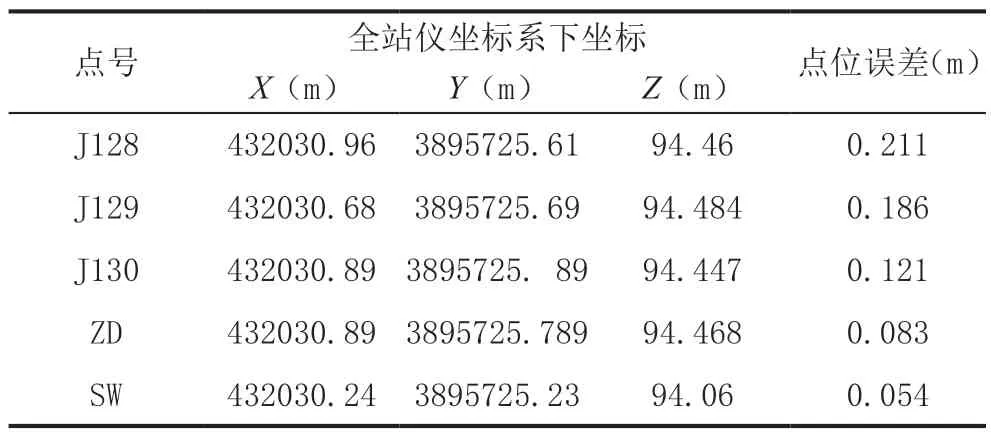
表4 中心点与边点的点位误差
通过数据分析可知,全站仪所测的边测点的点位误差大于其中心点位误差,因此可以得出,在同一测量精度下,全站仪的误差相对较大,而使用三维激光扫描仪获取的数据相对精确。
5 结论
本文通过实际案例和两种测绘方式的精度分析,发现三维激光扫描测量和全站仪测量在不同应用场景下各有优势。在近距离大型场景三维测量中,三维激光扫描技术采样速率快、点位精度高,在远距离测量时,坐标转换后的精度变低。在实际应用中应根据具体场景和需求选择合适的测量技术,提高测量精度和效率。
