融合Mar-G LSTM的流程生产工艺质量预测算法
2024-04-10阴艳超苏逸凡林文强蒲昊苒汪霖宇
阴艳超,苏逸凡+,唐 军,林文强,蒲昊苒,汪霖宇
(1.昆明理工大学 机电工程学院,云南 昆明 650500;2.云南中烟工业有限责任公司,云南 昆明 650024)
0 引言
流程工业对于国家经济的发展起到了至关重要的作用,影响力不容小觑,其安全高效生产及对生产过程指标变化趋势的准确预测已成为流程生产过程监控的重要任务,具有及其重要的战略意义[1]。与传统的离散制造有所不同,流程生产具有质量指标影响因素多且众耦合复杂,工艺参数时序特征显著,原料成分波动频繁等特点[2],也决定了流程生产在原料特性和生产工况等内外部条件变化时,如何及时感知预测工艺过程和产品质量发生的各种变化,进而通过反馈调控来调整工艺参数,保证生产全流程整体优化运行成为亟待解决的问题[3-4]。
传统的工艺质量指标预测方法大多依赖于对生产过程非稳定、非平衡和强非线性机理的理解,存在建模困难、预测精度低、可靠性难以保证等问题[5-8]。近年来,随着工业互联网技术的发展, 流程制造企业已采集了大量涉及生产运行、工艺、设备、过程、质量的历史数据[9-11]。

如何在不增加网络复杂度和深度的情况下,进一步提高模型的预测精度是构建工艺质量指标预测模型的核心工作。何俊强等[19]以马尔可夫链为基础建立了一种自适应的储能需求功率预测模型,该模型能够避免火电机组在调频时储能需求功率随机性强而导致难以实施监控的问题;WEI等[20]将马尔可夫链和正交分解法结合,提出一种能够在固态气流环境下预测空气中的气态污染物的方法,并运用于飞机机舱模型,结果证明了该方法的优势。以上研究都是基于相关实际工业数据开展,其构建的质量预测模型对制造业中产品质量预测均比较有效,也收获了大量有益的成果,但针对复杂生产线工艺数据的高维性和时序性特点,以及数据间强耦合性等问题,最终工艺质量的预测仍难以得到更为精准的预测结果。
为解决上述问题,本文提出一种基于马尔可夫优化的融合门控循环单元与长短期记忆网络(Markov chain Gate recurrent unit Long Short-Term Memory networks,Mar-G LSTM)的工艺质量预测模型。在工业生产流程中会产生大量的时序性工艺数据,各数据之间存在着强烈的相关性,门控循环单元网络适合处理具有时间关联的序列性数据,模型结构较为简单,训练参数相对较少,训练速度快,但会出现预测精度相对较低的情况。与门控循环单元网络相比,长短期记忆网络多一个“门”结构,模型参数多,内部结构相对复杂,训练精度高,因此将门控循环单元网络和长短期网络相结合,在提高预测精度和效率的同时解决了传统循环网络训练过程中易出现的梯度爆炸问题。考虑到生产流程中产生的数据具有很强的时序性,各时刻的质量指标数据都与历史工艺参数和质量指标之间有着非常密切的联系,利用马尔可夫模型可以从当前状态推断出未来的发展趋势,根据GRU-LSTM模型训练时产生的误差信息建立马尔可夫模型,在避免引入其他变量使模型更加复杂的情况下进一步提高工艺质量指标预测模型的预测精度。通过将Mar-G LSTM模型应用于某流程生产线的数据中进行验证,并与随机森林[21]、长短期记忆网络(LSTM)[22]、门控循环单元网络(GRU)[23]、卷积神经网络(Convolutional Neural Network,CNN)与门控循环单元组合网络(CNN-GRU)[24]以及与其他组合模型的预测结果相比,其预测精度具有显著提高,证实了Mar-G LSTM模型的有效性。
1 问题分析
近年来,大数据、物联网、人工智能等信息技术的快速发展,为流程制造车间带来了巨大的变革,其智能化水平得以显著提升,然而,如何在生产工程中精准地把控工艺质量,仍然是当今研究的热点问题。工艺质量指标预测需要以生产流程中大量的历史工艺数据作为输入,以此来准确预测产品的质量指标。以某制丝生产线为例,该生产线的松散回潮工序的工艺参数包括工艺热风温度、蒸汽自动阀门开度、工艺流量、加水累计量、加水流量和物料累计量,工艺质量指标包括出料温度和出料含水率。在实际生产过程中,流程制造过程复杂,容易受到多方面的影响,且传感器每6 s对数据进行采集并编制,每道工序将会产生大量的工艺数据,得到工艺数据集,各工序的工艺质量指标与历史工艺数据存在极强的相关性。但在实际应用中,数据间的时序依赖关系难以获取且数据量大,这导致无法提前对质量指标数据进行准确的预测,进而难以对生产过程进行合理的调控,最终成品的质量也无法获得保障。
工艺数据通常具有一定的时序性,传统的工艺质量预测模型难以捕获到时序信息,且数据量较大时训练速度难以得到保障,因而本文借助门控循环单元网络和长短期记忆网络模型进行工艺质量预测,它们共有的特征为在t时刻状态到t+1时刻进行更新,t+1时刻的输出由输入和先前的隐藏状态得来,以此来捕捉工艺时间序列中的依赖关系。门控循环单元网络模型内部每个隐层减少了几个矩阵相乘,加快了训练速度,而长短期记忆网络模型多出一个“门”结构控制信息的流动,其内部参数更多,拟合精度往往更高。由此将门控循环单元网络和长短期记忆网络模型结合,不仅可以提高预测效率,还可以保证预测精度,满足车间工艺数据在线预测的需求。尽管神经网络可以有效地处理复杂的工艺数据,但要想达到良好的预测效果,需要收集足够多的样本,以便于训练出更加稳健的网络结构,从而使得预测的准确性得到保障,若训练样本数据不足,预测结果往往会有所波动,影响预测准确性。针对以上情况,通过运用马尔可夫链分析神经网络模型的预测结果,根据真实值与拟合值之间误差的波动幅度和发展趋势得到状态转移概率矩阵,进而根据该矩阵对神经网络的拟合值进行修正,实现更加精准的工艺质量数据预测。
2 Mar-G LSTM深度时序网络模型
2.1 Mar-G LSTM网络结构
综合考虑工艺质量指标预测模型拟合精度和效率两个方面的原因,建立基于门控循环单元网络、长短期记忆网络与马尔可夫链的组合预测模型,具体包括3个部分:第一层结构采用门控循环单元网络,发挥其网络结构较为简单、参数少的优势,提高模型的训练时间和测试时间,从而保证组合模型的预测速度;第二层为长短期记忆网络模型,LSTM模型的参数较多,结构较复杂,对时序性数据预测具有较高的准确性,将二者结合能够同时提高预测精度并减少预测时间;第三层结构采用马尔可夫模型,利用马尔可夫模型能够捕获到神经网络训练过程中产生的预测误差,并根据误差划分为不同的状态空间,从而得到状态转移概率矩阵,根据矩阵对神经网络的预测值进行修正,以此进一步提升预测的准确性。 Mar-G LSTM网络结构如图1所示。

图1 Mar-G LSTM结构图
2.2 门控循环单元
流程工业生产中,伴随着大量设备和智能产品的流入,工业数据的存储量大规模增长。由于数据量庞大,各工艺之间有很强的时序性,工艺质量预测问题仅通过分析当下工艺数据很难精确地预测出未来的产品质量,从而使得工艺质量的预测变得更加困难,因此需要同时引入历史工艺数据集进行建模。传统的预测模型在处理数据量较大的问题时,往往训练时间较长,难以满足在线预测的要求,而以循环神经网络(Recurrent Neural Networks,RNN)为基础改进后的门控循环单元网络,不但能够避免RNN在时间步数较大或较小时引发的梯度爆炸和梯度弥散的问题,而且其内部结构相对于RNN网络的另一种变体长短期记忆网络模型少一个“门”结构,参数更少,训练速度更快。为保证在流程工业生产中进行实时预测,引入门控循环单元网络提高模型的训练时间。将历史工艺数据归一化后作为网络的输入,获取其潜在的深层关联时序信息。
门控循环单元网络GRU的单元结构如图2所示,它采用了隐藏状态来传递信息,并且建立在长短期记忆网络的基础上,将输入门与遗忘门合并成一个更新门,从而简化了模型的组成,极大地降低了模型的复杂程度,有效地加快了模型的训练进程。然而,实际应用中,由于其内部参数变得很少,很难达到理想的训练效果。

图2 门控循环单元网络结构图
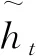
rt=σ(Wr·[ht-1,xt]+br),
(1)
zt=σ(Wz·[ht-1,xt]+br),
(2)
(3)
(4)
其中:Wr、Wz、Wh分别为重置门、更新门和隐藏状态的权重矩阵;br、bz、bh为偏差向量;σ为激活函数Sigmoid,用于将值控制在[0,1]之间;tanh激活函数用于调节流经网络的信息,并归一化在[-1,1]之间。
当更新门zt的值为0,重置门rt的值为1时,GRU的结构与RNN一致;当更新门zt的值为0,重置门rt的值也为0时,信息状态ht仅与t时刻输入的工艺数据xt有关;当更新门zt的值为1,重置门rt的值为0时,信息状态ht仅与t-1时刻的工艺数据输出信息ht-1有关。
2.3 深度LSTM网络模型
长短期记忆网络(LSTM)的工艺参数预测模型的单元结构如图3所示,共包括3个“门”结构和细胞状态信息,即输入门(Input gate)、遗忘门(Forget gate)、输出门(Output gate)、,3个“门”结构的存在有助于保护和控制信息,而其核心结构细胞状态则决定工艺信息保留的程度。
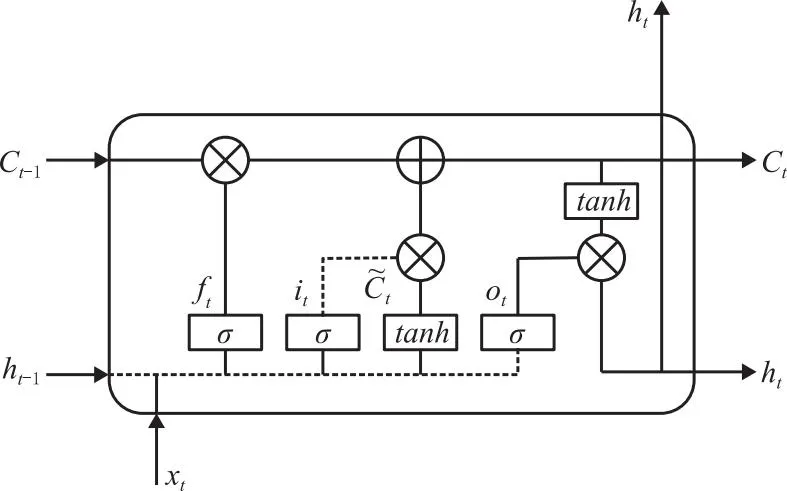
图3 长短期记忆网络结构图
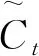
ft=σ(Wf·[ht-1,xt]+bf),
(5)
it=σ(Wi·[ht-1,xt]+bi),
(6)
(7)
(8)
ot=σ(Wo·[ht-1,xt]+bo),
(9)
ht=ot·tanh(Ct)。
(10)
其中:Wi、Wf、Wc和Wo分别为输入门、遗忘门、状态更新层和输出门的权重矩阵;bf、bi、bc和bo分别为输入门、遗忘门、状态更新层和输出门的偏差向量;σ为激活函数Sigmoid,用于将值控制在[0,1]之间;tanh激活函数用于调节流经网络的信息,并归一化在[-1,1]之间。
由于门控循环单元网络较为精简的内部结构,其预测精度难以得到保证,为进一步提升模型的预测精度,同时避免因部分产线工艺数据不足无法精准建模等问题,在门控循环单元网络的基础上融入长短期记忆网络模型[25]。长短期记忆网络模型使得信息在跨过多个时间步依然可以保存下来,同时也允许梯度跨过多个时间步进行传递,其结构较复杂,训练参数更多,预测精度往往更高。基于门控循环单元网络,利用长短期记忆网络对历史工艺数据中的时序信息进行提取,并使用Relu函数进行激活,最后添加Dense层,以增强时间序列与预测结果之间的关联,并将输出结果进行反归一化,从而得到GRU-LSTM组合网络的预测结果。GRU-LSTM结构图如图4所示。
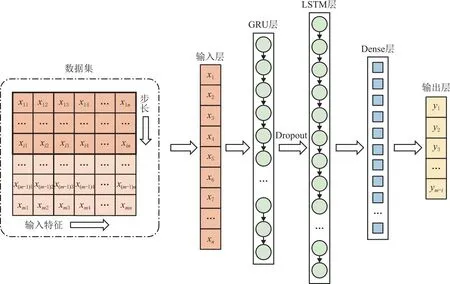
图4 GRU-LSTM网络结构图
2.4 G LSTM的马尔可夫优化
马尔可夫链(Markov chain)[26]也称为离散时间马尔可夫链(discrete-time Markov chain),最早是由俄国数学家安德雷·马尔可夫提出并对其进行研究,主要应用于分析当前和未来的变化趋势,以便更好地把握和预测未来的发展情况。马尔可夫链在工艺质量指标预测模型中具有以下概念:
(1)状态空间 事件在某时刻呈现的某种结果称为“状态”,所有“状态”构成的集合为状态空间。在Mar-G LSTM模型中,“状态”指GRU-LSTM模型拟合后的预测值与真实值之间的相对残差,根据相对残差的波动情况和趋势划分为不同的区间范围,构成Mar-G LSTM状态空间集合。
(2)状态转移 在事件发展的过程中,伴随时间的变化由一个状态向另一个状态转变,称为状态转移。
(3)状态转移概率 事件在t时刻处于某一状态,伴随时间的变化,在下一时刻转移到下一个状态概率称为状态转移概率。在工艺质量预测模型中指训练数据的相对残差随着采集时间的变化状态进行转移的概率。例如从状态⊗Sa转移到状态⊗Sb的状态转移概率的计算方式如下所示:
(11)
其中:Eab为从⊗Sa状态经过一步转移到⊗Sb状态的样本数,Ea为位于⊗Sa状态的样本数。
(4)状态转移概率矩阵 在时序性工艺数据中,每个时刻的数据都处于一种状态,而状态转移概率矩阵由各数据从当前时刻的状态转移到下一时刻状态所有可能的概率构成。假定共有n种状态,Pab为从状态⊗Sa经过一步转移到状态⊗Sb的状态转移概率,即可得到状态转移概率矩阵P:
(12)
若预测的工艺质量指标数据的相对残差在某一时刻处于状态⊗S1,则在下一时刻它可能转移到状态⊗S1,⊗S2,…,⊗Sn中的任一状态,状态转移概率Pab满足以下条件:
(13)
(14)
由于神经网络训练后的网络结构往往存在一定的不完全稳定性,影响模型的拟合效果,而根据马尔可夫链的性质可知,它能有效地预见并消除随机因素产生的误差。因此为了进一步提高工艺质量预测模型的精度,在GRU-LSTM组合网络完成预测后引入马尔可夫模型,通过计算训练数据工艺质量指标实际值序列和预测值序列之间的相对残差进而划分状态空间,根据状态空间计算训练数据的状态转移概率矩阵,以状态转移概率矩阵为依据预测工艺质量指标下一时刻可能所处的状态并进行修正,提高模型的拟合精度。具体如下:
(1)计算训练集实际值序列和预测值序列的相对残差序列,以波动性大且较为平稳的相对残差序列划分模型的状态空间,相对残差ηi和状态空间⊗Sa的计算公式分别为:
(15)
(16)
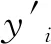
(2)根据相对残差序列确定每个训练数据所处的状态空间,结合数据间的状态空间变化情况计算出训练集样本的n步状态转移概率矩阵P(n):
(17)
(18)
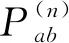
(3)根据求得的状态转移概率矩阵得到下一个时刻的工艺数据最大概率所处的状态空间,进而对GRU-LSTM模型拟合出的工艺质量指标预测值进行修正,得到更为精准的预测结果。具体修正方法如式(19)所示:
(19)
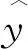
3 算例与结果分析
3.1 Mar-G LSTM深度时序网络模型的预测性能
3.1.1 实验环境
为验证Mar-G LSTM模型的普适性和精确度,笔者进行了多次实验。本次实验平台为个人计算机,CPU为Core(TM) i7-12700,配备32.0 GB的RAM,GPU为NVIDIA GeForce RTX 4090。并使用Window 11操作系统,通过在Keras框架下和Python 3.6的基础上,利用PyCharm社区版集成开发工具建立预测模型,以此来实现Mar-G LSTM算法模型的应用。
3.1.2 实验数据
本次实验以某企业流程生产线的一道工序时序数据作为数据集,该生产线的整体工艺流程包括:松散回潮、一级加料、二级加料、切叶丝、叶丝增温增湿、叶丝干燥和加香,实验针对松散回潮工序为主要案例进行分析。作为制丝生产工艺中首道工序,松散回潮是制丝生产过程中至关重要的一步,也是核心工序之一,它旨在通过调节烟片的含水率和温度来显著提升叶丝的耐加工能力,从而使得最终的卷烟产品具有更好的口感和更优良的质量。在制丝生产线上,传感器每6 s收集一次样本数据,并将其存储在制造执行系统(Manufacturing Execution System,MES)数据库中,以便获取历史记录,排除所有离散奇异点后,最终作为实验数据的主要来源。
为验证Mar-G LSTM算法的有效性,本实验使用生产线采集的2022年10月8日~2022年10月12日之间的数据作为数据集进行验证,数据集部分原始数据如表1所示,共5000组数据。在数据集中共包含6个工艺参数,分别为松散回潮的工艺流量、加水流量、工艺热风温度、加水累计量、物料累计量和蒸汽自动阀门开度,质量指标为松散回潮出料温度,每组数据都包含其采集的日期信息。由于神经网络模型需要大量的样本数据进行训练以保证网络结果的稳定,将采集的工艺数据按照4∶1的比例进行划分,其中训练集数据4 000条,测试集数据1 000条。

表1 数据集部分原始数据
3.1.3 实验参数
获取数据后,为避免各工艺参数之间因量纲的差异影响模型的拟合效果,首先对各工艺数据进行归一化处理,使得原始数据能够被统一到[0,1]范围内,从而更好地进行综合对比评价,具体计算方法见式(20)。GRU-LSTM模型的参数如表2所示。在工艺参数预测模型中,第一层为GRU模型,神经元个数设置为256个,激活函数为Relu,学习率为0.001,return_sequences参数设为True,Dropout率设为0.2;第二层为LSTM模型,神经元个数设置为256个,激活函数为Relu,学习率为0.001;batch_size为128,优化器选用adam,为防止网络层堆叠不稳定对预测结果产生影响,在最后加入Dense全连接层进行调节,层数为1层,将最终的输出结果进行反归一化,得到下一时刻出料温度的预测结果。
(20)
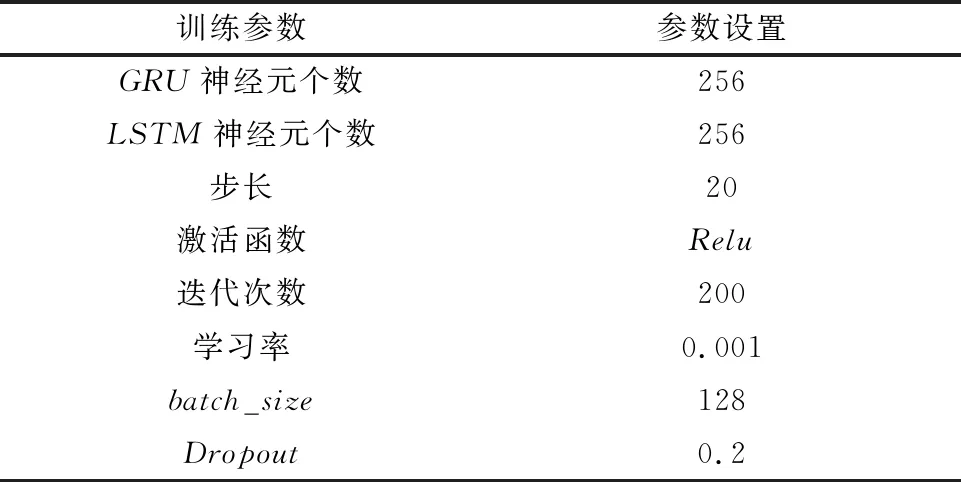
表2 训练参数设置
其中,Xmin、Xmax分别为原始各工艺数据序列中最小值和最大值;X为当前工艺数据值;Xscale为经过归一化后的工艺数据值。
在训练时间步长的设置上选取的参数n_steps=20,即用20组历史工艺数据来预测第21条的工艺质量指标,如此滚动计算直至遍历所有数据输出预测结果。当对步长进行选取时,应保持一个适中的范围,步长过大会导致模型忽略前期的数据,而步长太小又会使得模型难以捕捉到潜伏在时间序列中的信息,从而降低了网络模型的准确性。通过对模型进行调试认为将步长设为20预测效果最佳。
3.1.4 实验过程
首先,提取GRU-LSTM模型松散回潮工序出料温度的训练集拟合值,计算相对残差值(如式(15)),相对残差的结果侧面反映了拟合值预测误差的大小,其越接近0,则出料温度真实值与拟合值之间的误差越小。最终计算的相对残差结果如表3所示,按照2.4节所述对拟合值进行修正,具体如下:

表3 训练集的状态空间划分
(1)状态区间划分
根据训练集出料温度的实际序列和GRU-LSTM模型预测序列的差异,进而划分状态区间⊗Sa=[Sa1,Sa2]。本实验将拟合值划分为如下4个状态:①预测值状态(⊗S1):即相对残差在[-0.008,-0.003)之间;②预测值状态(⊗S2):即相对残差在[-0.003,0)之间;③预测值状态(⊗S3):即相对残差在[0,0.004)之间;④预测值状态(⊗S4):即相对残差在[0.004,0.014]之间。由此将拟合值划分到对应的状态空间,如表3所示。
(2)状态转移概率矩阵
根据表3中训练集所属的状态空间,可以得到松散回潮出料温度的一步状态转移概率矩阵:
(21)
(3)组合模型预测
由表3可知,第4000条出料温度处于⊗S2状态,由式(21)状态转移概率矩阵可知,经过一步转移后,第4001条出料温度最有可能处于⊗S2状态,据式(19)即可得到马尔可夫修正后的拟合值。在对第4002条出料温度的状态空间进行分析时,将第4001条出料温度所处的状态空间作为已知数据,按照上述方法重复,可以计算得到其余数据的马尔可夫修正后的拟合值,若测试集的相对残差超过划分的状态空间范围,则按⊗S1状态或⊗S4状态进行修正。马尔可夫修正前后拟合值如表4和图5所示,计算两种模型的相对残差得到平均相对残差值,如表5所示。
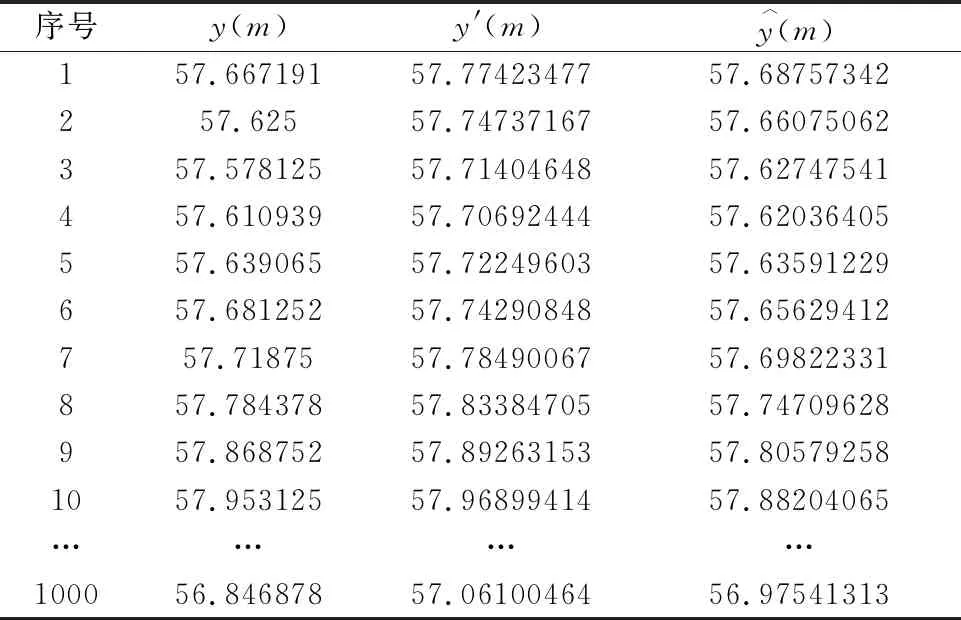
表4 测试集真实值、GRU-LSTM拟合值与马尔可夫修正值情况
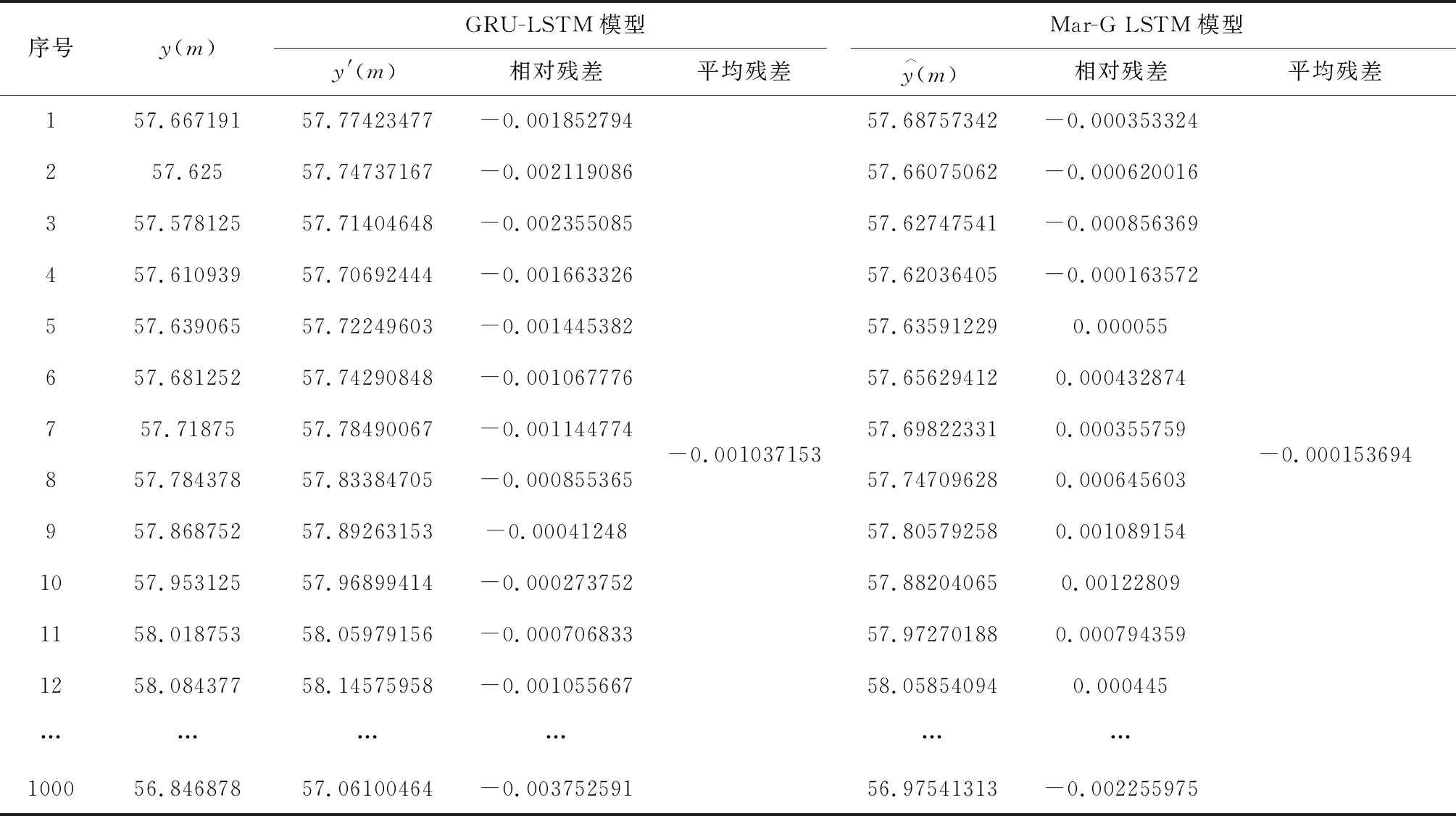
表5 GRU-LSTM和Mar-G LSTM预测结果相对残差对比
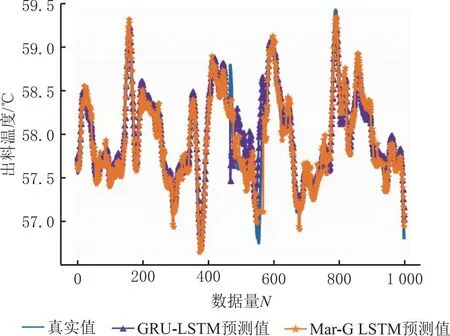
图5 GRU-LSTM和Mar-G LSTM与真实值拟合图
3.1.5 模型评价指标
为验证本文所提工艺质量指标预测模型的性能,选择使用决定系数R2、均方根误差RMSE、平均绝对误差MAE和均方误差MSE作为模型的评价指标。一般情况下,R2越接近1,则模型的拟合效果越好,RMSE、MAE和MSE的值越小,则回归分析的差异程度越低,模型的拟合性能越好。各指标的计算公式如下:
(22)
(23)
(24)
(25)
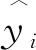
3.2 消融实验
本文通过消融实验验证Mar-G LSTM模型在提升工艺质量指标预测准确率方面的有效性,共使用5种模型训练同一组工艺数据,并将拟合结果进行对比,5种模型分别为传统神经网络门控循环单元(GRU)网络和长短期记忆(LSTM)网络,GRU-LSTM组合网络,以及分别经马尔可夫修正后的门控循环单元网络和长短期记忆网络。实验结果如表6和图6所示。消融实验各模型的相对残差对比结果如表7和图7所示。
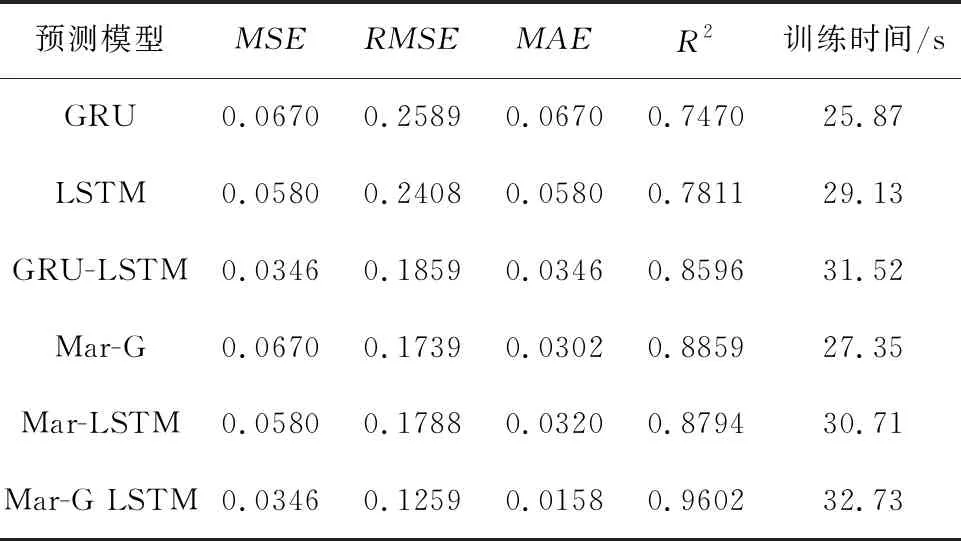
表6 消融实验预测分析表
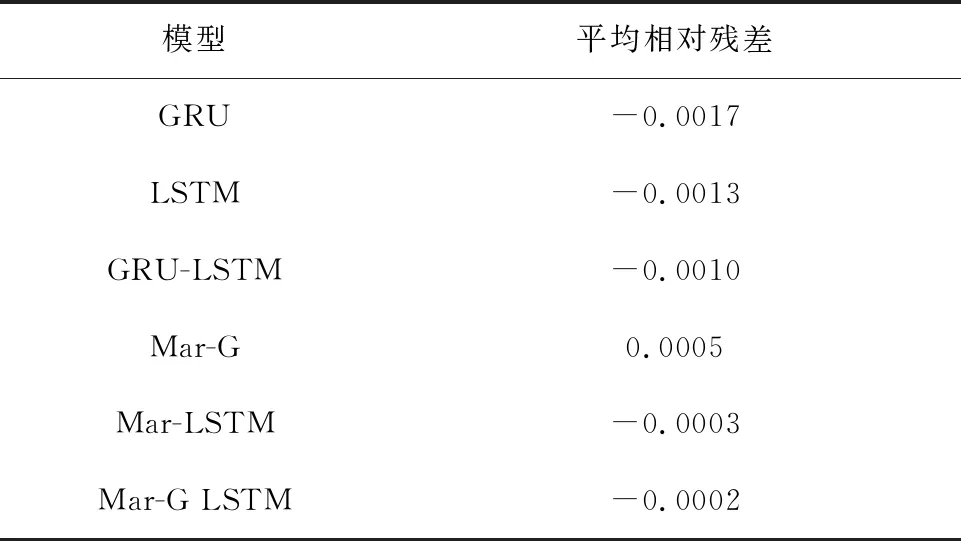
表7 消融实验平均相对残差对比
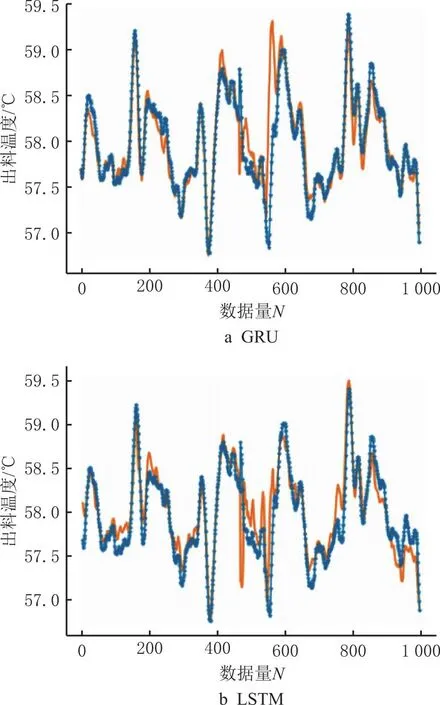
图6 消融实验预测结果对比
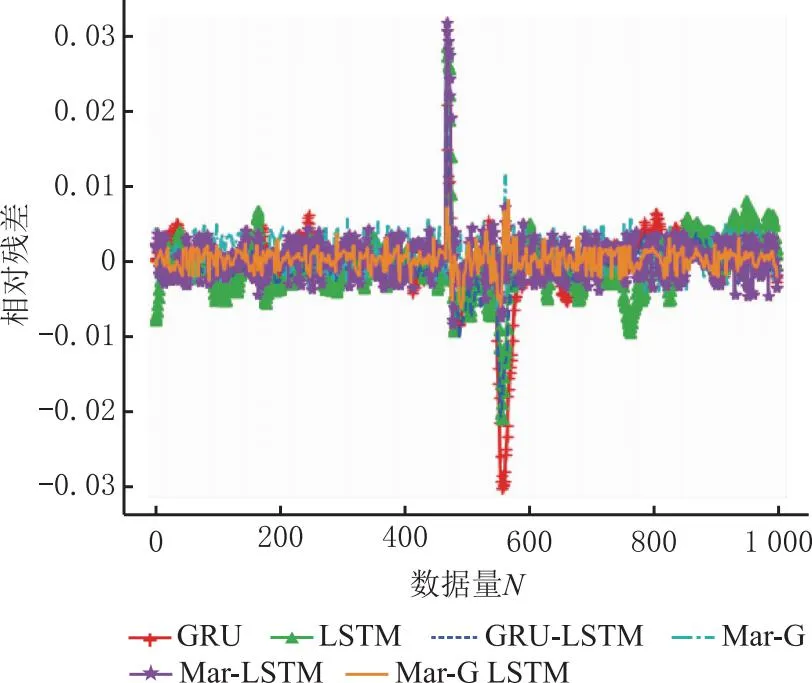
图7 消融实验相对残差对比
由表6中的实验结果比较可知,GRU-LSTM模型的预测精度优于单层门控循环单元和长短期记忆网络模型。虽然单层的网络结构参数较少,训练时间相对较短,但模型的学习能力相比于组合网络有所下降,相比之下,GRU-LSTM组合的网络结构复杂且参数多,而训练时间相比于预测性能较好的长短期记忆网络仅增加了2.39s。引入马尔可夫模型后,单层门控循环单元网络和长短期记忆网络的拟合度均有10%左右的提高,但训练时间仅增加了1.5s左右。由实验可证明本文所提Mar-G LSTM模型结合门控循环单元网络训练速度快、长短期记忆网络预测精度高和马尔可夫模型消除误差的优势,有效提高模型的预测精度和预测效率。
3.3 对比试验
为说明本文提出的模型在车间工艺质量预测中的优势,将本文提出的Mar-G LSTM模型的预测效果与传统的机器学习模型随机森林、XGBoost,神经网络预测模型RNN和CNN-GRU,以及利用马尔可夫修正后的组合模型Mar-RNN、Mar-CNN-GRU的拟合效果进行了对比,预测结果的各评价指标如表8所示,预测对比图如图8所示,各对比模型平均相对残差结果如表9所示,相对残差对比结果如果9所示。可见,在使用Mar-G LSTM模型进行质量指标预测时,其拟合度较其他6种模型均有明显提高,体现了本文模型在预测精度方面的优势。传统的机器学习模型虽然训练速度快,但在处理数据量较大的情况时,拟合度较低,无法保证预测精度;组合网络模型相比于单层神经网络模型,其内部网络结构复杂参数较多,因此在训练模型的时间上有所耗费。由表8可以看出,在保证85%以上的预测精度情况下,经过马尔可夫修正后的GRU-LSTM组合网络模型相较于修正后的RNN模型时间上仅增加了4.79 s,而拟合度提高了10%左右,相较于马尔可夫修正后的CNN-GRU模型,Mar-G LSTM模型训练时间缩短了1.33 s,拟合度提高了3.86%,可以说明本文模型在保证预测效率的情况下,提高了模型的预测精度。
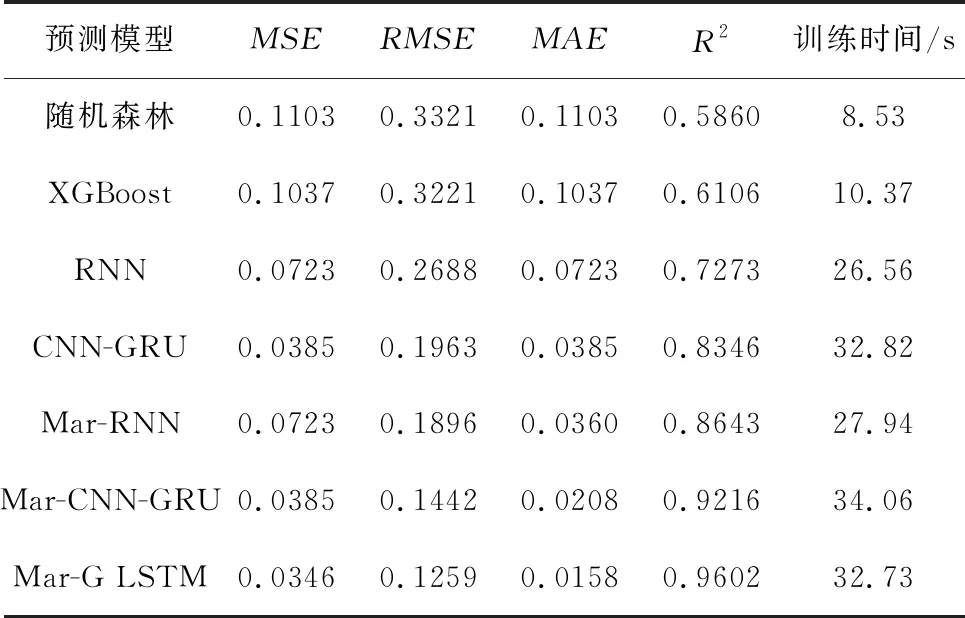
表8 对比模型预测结果评价指标
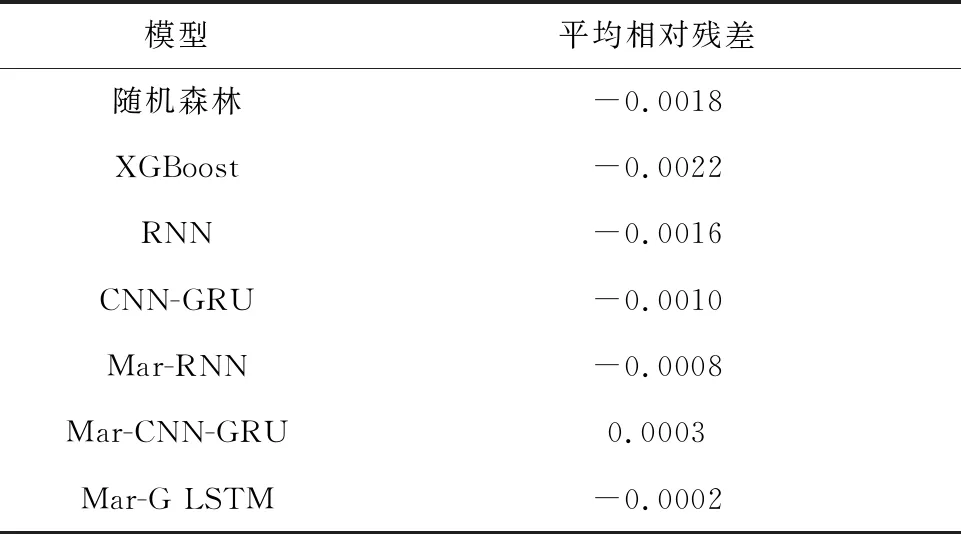
表9 对比模型平均相对残差

图8 对比实验预测结果对比
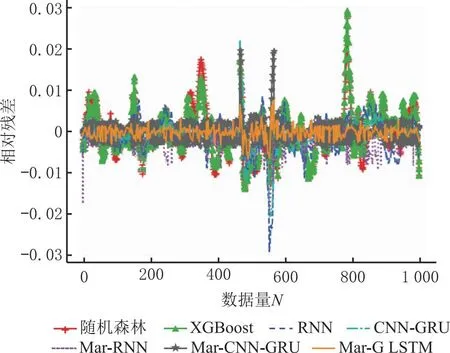
图9 对比实验相对残差对比
3.4 泛化性验证
在实际流程生产过程中,预测模型若仅适用于某道工序是无法进行应用的,模型的泛化能力也是判断模型是否适用于生产线的重要标准。为验证本文所提Mar-G LSTM模型的泛化能力,将模型应用到一级加料和薄板干燥工序中预测其质量指标。
(1)一级加料 该工序共包含7项工艺参数,分别为料液流量、料液累计量、料液温度、工艺流量、加水流量、物料累计量和工艺热风温度,工艺质量指标为出料温度,共收集5000条工艺数据生成新的数据集。
(2)薄板干燥 该工序的工艺参数共包含10项,分别为叶丝增温增湿工艺流量、切叶丝含水率、薄板干燥热风风速、薄板干燥热风温度、叶丝增温增湿蒸汽流量、叶丝冷却出料含水率、薄板干燥Ⅰ区筒壁温度、薄板干燥Ⅱ区筒壁温度、叶丝干燥筒壁Ⅰ区蒸汽阀门开度以及叶丝干燥筒壁Ⅱ区蒸汽阀门开度,工艺质量指标为出料温度,共收集5000条数据作为新的数据集。
本文提出的Mar-G LSTM模型在一级加料和薄板干燥两道工序上的测试结果如表10所示,拟合情况如图10和图11所示。由预测结果可以看出Mar-G LSTM模型在不同工序下的预测精度均在95%以上,证明该工艺质量指标预测模型具有良好的泛化性能,能够有效地应对制丝生产线不同工序的工艺变化。
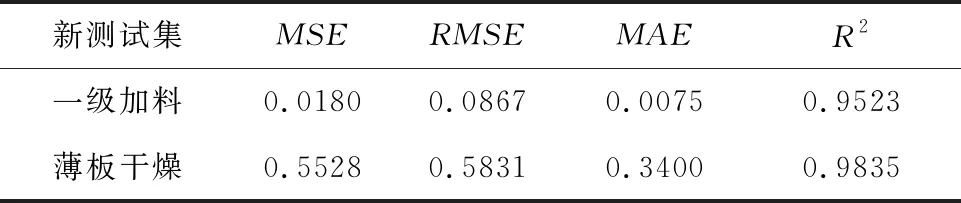
表10 不同工序Mar-G LSTM模型泛化能力测试结果
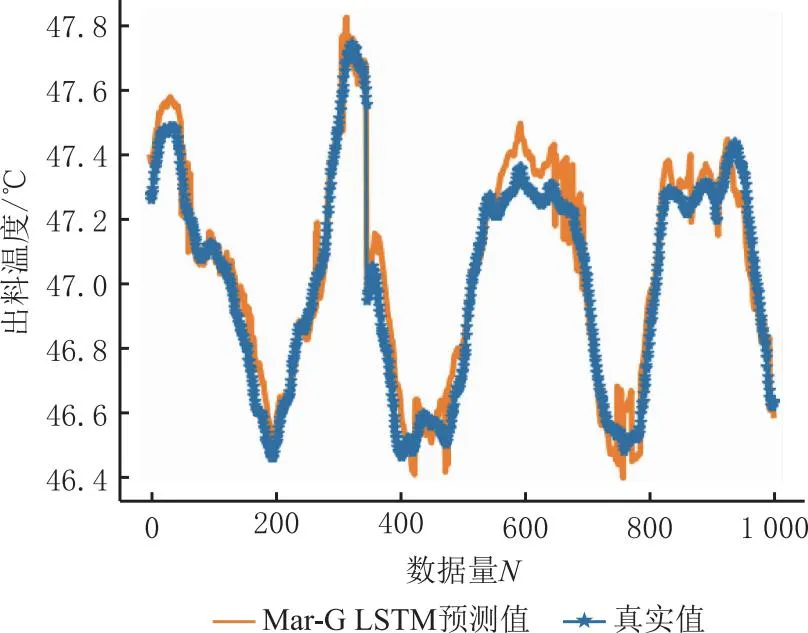
图10 一级加料预测结果对比
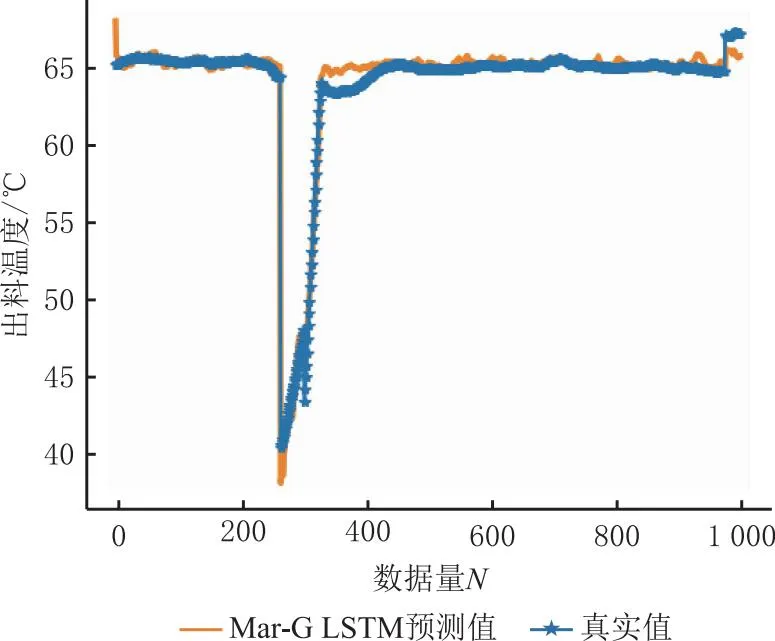
图11 薄板干燥预测结果对比
4 结束语
针对目前工艺质量预测模型对于具有关联性和时序性特征的数据进行预测时其精度较低且预测周期较长的问题,本文提出一种基于Mar-G LSTM的车间工艺质量预测算法模型,并对该方法的预测效果进行了实例分析和评估,主要结论如下:
(1)GRU-LSTM模型在工艺质量预测中能有效提升曲线拟合精度。在实验中GRU-LSTM模型的平均相对残差相对门控循环单元网络和长短期记忆网络模型分别下降了0.07%和0.03%,这一结果表明GRU-LSTM模型的工艺质量预测的准确性优于单层网络模型。
(2)在GRU-LSTM模型后引入马尔可夫模型进行修正,能够更加准确地描述工艺质量指标的变化规律,提高预测精度。在对比实验中,Mar-G LSTM模型的相对残差、RMSE、MAE、MSE均小于其他6种预测模型,决定系数R2明显大于其他预测模型。实验结果表明,本文所提预测模型在工艺质量指标预测中误差小,预测结果更为准确,对于在生产线中提高产品质量的稳定性具有一定的意义。
本研究验证了将基于深度学习的神经网络模型与马尔可夫链结合完成不同工序的车间工艺质量预测,为实际车间生产中完成在线预测提供了新的方向,未来将运用在线工艺数据验证本网络模型实用性并加以改进。
