基于K均值聚类算法的谐振接地系统故障区段定位方法

黄 劼 汪逸帆 林叶青 胡荔丹 王丹豪

基于K均值聚类算法的谐振接地系统故障区段定位方法

黄 劼 汪逸帆 林叶青 胡荔丹 王丹豪

（国网福建省电力有限公司福州供电公司，福州 350004）

现有的谐振接地配电网单相接地故障定位方法存在通信依赖过度、特征分析复杂和阈值设置困难等问题，现场运行的适用性较低。本文基于深度融合智能开关在配电网中的应用，研究三相电流变化量的波形特征，提出基于K均值聚类算法的就地选段方法。该方法提取各区段数据特征量，发挥K均值聚类算法无监督学习的优点，使各检测节点只需处理本地故障信号，从而减轻通信压力。利用仿真和现场数据验证该方法的可行性，结果表明，该方法在多种故障工况下都表现出较高的可靠性，并且能够较好地适应现场环境。

谐振接地系统；单相接地故障；就地选段；K均值聚类；非监督学习

0 引言

配电网和用户直接相连，其结构比高压输电网复杂，且电压等级多变。配电网发生故障的次数可占整个电力系统故障次数的80%以上，而单相接地故障占配电网故障的绝大多数[1-2]，因此如何快速切除配电网单相接地故障已成为影响电网安全稳定运行的关键因素。

故障选段方法可分为主动式和被动式两类：主动式选段，即在故障后通过注入特定频段信号实现选段；被动式选段，即利用故障前后电气量的变化实现选段。主动式选段成本较高、对复杂工况的适应性较差，因此被动式选段逐渐成为研究热点。

被动式选段基于稳态量或暂态量，基于稳态量的选段方法包括零序电流比幅法[3]、零序功率方向法和谐波电流法等。当配电网发生单相接地故障后，暂态过程通常持续1～2个周波，该过程波形特征明显[4]，可使用相分量或零序分量等进行故障选段，因此基于暂态量的选段方法[5-7]备受关注。分析暂态信号常使用傅里叶变换、希尔伯特-黄变换及小波变换等算法。

目前，大多数选段方法都存在一个缺陷：发生单相接地故障时，所有终端单元[8]都要将故障数据上传至主站再进行数据处理，但该过程传输的数据量很大，需要花费较多时间，若通信发生故障，则传统选段方法无法正常运行[9]。随着就地选段概念的提出，配电网一二次融合技术[10]随之发展，深度融合智能开关应运而生，该设备仅需采集本地信息，通过算法实现故障选段，无需与主站通信。

近年来，国内外研究人员将人工智能技术应用于故障选段中，实现对故障特征量的智能化识 别[11-13]，并取得了一定成果。本文采用三相电流变化量波形数据研究区段分布的波形特征，提取各区段的故障特征量，考虑多维评价指标，以降低故障选段的错误率。

本文首先分析暂态三相电流特征，然后介绍特征量融合和K均值聚类的基本原理，并详细说明利用K均值聚类算法进行故障区段定位的过程，最后使用仿真和现场数据对本文提出的方法进行验证。

1 暂态三相电流特征分析

配电网典型拓扑结构为辐射型网络，中性点接地方式采用经消弧线圈接地[4]，在不考虑线路阻抗的情况下，简化10kV谐振接地系统如图1所示。图1中，A、B和C为三相电源电压，L为流经消弧线圈的电感电流，和L分别为消弧线圈的电感和电阻，f为过渡电阻，C（=1, 2,…,）为第条馈线的对地电容。

故障发生前，配电网正常运行，此时任意区段首端的三相电流为

式中：u0为正常运行时的中性点对地电压；ijHA、ijHB、ijHC分别为流过区段j的三相电流；ijHAC、ijHBC、ijHCC分别为流过区段j的三相电容电流；ijHAL、ijHBL、ijHCL分别为流过区段j的三相负荷电流；CjA、CjB、CjC分别为区段j的三相对地电容值。对于同一三相电压源，各区段相电流的表示形式是一样的，因此各区段同相电流波形相似，只是幅值有所差异。

当馈线发生A相接地故障时，故障区段，即故障点上游和本区段，首端的三相电流为

健全区段，即故障点下游和健全馈线区段，首端的三相电流为

式中：iFA、iFB、iFC为流过区段的三相电流；iFAC、iFBC、iFCC为流过区段的三相电容电流；iFAL、iFBL、iFCL为流过区段的三相负荷电流；CA、CB、CC分别为区段的三相对地电容值。与区段的负荷电流特性一致，区段的负荷电流在故障后也保持不变，即iAL=iFAL=iHAL，iBL=iFBL=iHBL，iCL=iFCL=iHCL。

在工程中，故障选段易受到负荷干扰[15]。通过计算相电流变化量可去除负荷电流，避免其对选段造成影响，方法如下。

式中：D为故障前后一个周期的相电流变化量；0为故障发生时刻；为周期；(0+) 为故障后一周期的相电流；(0-) 为故障前一周期的相电流。

由式（1）、式（2）可得区段的故障相电流变化量为

设故障相为A相，故障电流f为

式中，∑为总对地电容值。式（5）可整理为

假设三相参数对称，中性点电压0=0，区段的故障相电流变化量可简化为

由式（1）、式（2）可得区段的非故障相电流变化量为

由式（1）、式（3）可得区段的三相电流变化量为

综上，发生单相接地故障时，三相电流变化量波形有以下特点：在故障区段，故障相与非故障相波形有较大差异，而非故障相波形基本相同；在健全区段，三相波形基本相同。

2 故障区段定位方法

2.1 相电流变化量的特征融合

为表征区段的故障特征，本文选段方法融合多种评估波形的特征量，采用余弦相似度、欧氏距离、偏移系数和奇异值这4种评价指标，实现相电流变化量的特征融合。

1）余弦相似度

余弦相似度用于评估两个向量的相似性，该特征量反映波形之间的相似程度。对于相电流变化量波形，其余弦相似度为

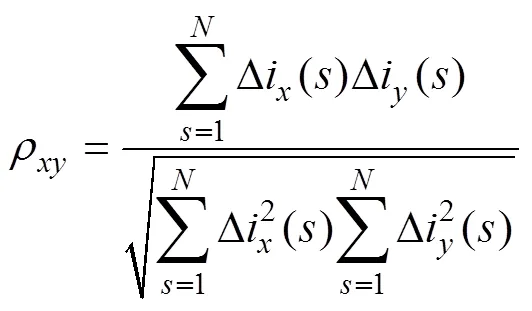
在故障区段，故障相与非故障相波形的相似性较低，余弦相似度通常为负数，而非故障相之间波形的相似性较高，余弦相似度接近1；在健全区段，三相波形的相似性较高，三个余弦相似度都较大。因此，将最小的余弦相似度作为第一维故障特征量。

2）偏移系数

偏移系数用于反映多个波形间的不平衡程度，该特征量不受信号正负影响，在工程中即使互感器极性接反，也不会干扰特征量。对于相电流变化量波形，其偏移系数为

式中：为波形间的偏移系数，越大表示波形之间的不平衡度越大；Di为相的电流变化量，即DA、DB和DC，通过式（13）对应得到A、B和C。

在故障区段，故障相与非故障相波形更不平衡，偏移系数约为1；在健全区段，三相波形较平衡，偏移系数较小。因此，将偏移系数作为第二维故障特征量。

3）奇异值

将相电流变化量波形数据表示为向量=[12…x]，对向量进行变换得到Hankel矩阵，再对矩阵进行奇异值分解，以提取波形的奇异值。

令+=，=0.3，=0.7，则有

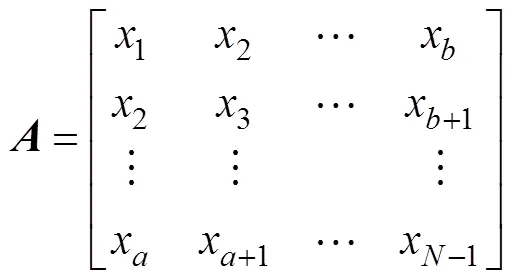
对进行奇异值分解得到

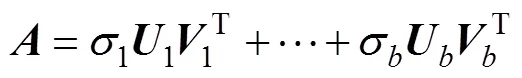
选取矩阵的任意一个奇异值作为描述相电流变化量波形的特征量，各区段可分别获得A、B和C三个奇异值。由于其他特征量的取值范围为[-1, 1]，为便于对比，对三个奇异值进行处理，使其取值也在[-1, 1]内，方法如下。

式中，表示奇异值，越大表示波形之间幅值差异越大。在故障区段，故障相与非故障相波形的幅值差异较大，接近于1；在健全区段，三相波形的幅值差异较小，接近于0。因此，将奇异值作为第三维故障特征量。

4）欧氏距离

欧氏距离用于衡量两点间的绝对距离，可评估波形之间的差异。为便于分析，首先对相电流变化量波形数据进行归一化。

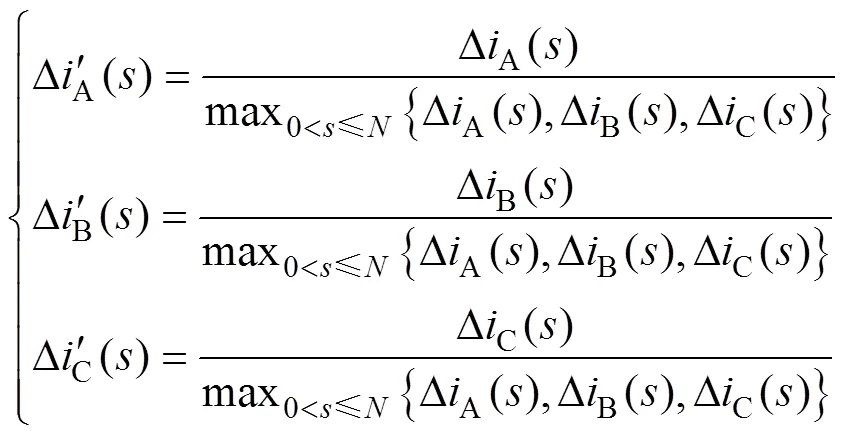
波形间的欧氏距离为

将式（18）求出的欧氏距离缩小为原来的1/10，使之符合前三个特征量的取值范围。在故障区段，故障相与非故障相波形相距较远，而非故障相之间相距较近；在健全区段，三相波形都相距较近。因此，将最大的欧氏距离作为第四维故障特征量。

将上述故障特征量融合，构建4维故障特征向量表示各区段的故障特性，再通过K均值聚类算法识别区段类型。该方法充分利用各种故障特征，改进了选段判断标准，降低了误报率，从一定程度上克服了以单特征量选段的局限性。

2.2 配电网一二次深度融合智能开关的应用

一二次深度融合智能开关（下称智能开关）能够对电压和电流数据进行采集分析，并进行智能化故障诊断。智能开关包括电压和电流传感器、重合闸、联动装置及控制终端等组件，如图2所示。当发生单相接地故障时，智能开关可以对现场数据进行分析判断，快速隔离故障区段，有助于保障非故障用户的持续供电，同时不依赖通信，提高运维人员的工作效率。

图2 一二次深度融合智能开关

智能开关识别出故障区段后，将根据阶梯原则执行保护动作[16]。保护时延通常在ms级别，为确保能快速准确动作，智能开关的切换时间约为30ms。智能开关数量越多，则疑似故障区域越小，但投资成本也相应提高，在兼顾可靠性和经济性的前提下，可只在故障率高的区段安装适当数量的智能开关[17]。

2.3 基于K均值聚类算法的区段定位过程

聚类分析是数据挖掘的主要任务之一，属于无监督学习，不需要训练过程，具有高效直观的优点，因此在许多领域得到广泛应用[18]。聚类算法不依赖现场故障数据，能更好地适应现场环境的复杂变化。本文采用K均值聚类算法，避免传统方法繁琐的训练过程，具体实现如下。

1）输入数据集：向各检测节点输入K均值聚类算法所需的4维故障特征向量。

2）初始化算法参数：将聚类数目设置为2，以区分区段类型。

3）初始化聚类中心：随机生成两个聚类中心。

4）数据聚类：找出离数据点最近的聚类中心，并将其归类。

式中：为第个输入数据；X为的第维数据；为第个聚类中心；C为的第维数据；表示聚类中心的维度，=4。

5）更新聚类中心：计算归类后所有数据的平均值，形成新的聚类中心。

6）迭代计算：继续进行数据聚类，更新聚类中心，直到聚类中心数值收敛。

7）输出结果：获得各检测节点的选段结果。

如果聚类算法仅使用本区段数据，那么将无法形成区内、外两个聚类中心，因此还需少量其他数据，与现场数据一起聚类，以确定该区段类型。基于K均值聚类算法的区段定位流程如图3所示。

图3 基于K均值聚类算法的区段定位流程

3 仿真研究

3.1 PSCAD/EMTDC仿真

基于PSCAD/EMTDC仿真软件搭建的10kV谐振接地系统仿真模型如图4所示，该模型包括110kV三相电源、消弧线圈、主变压器、配电变压器、Z型变压器、5条含架空线路和电缆线路的馈线及18个节点。图4中，o和c分别为架空线路长度和电缆线路长度。工频为50Hz，采样频率为10kHz，负载功率为0.5MW。

主变压器、配电变压器和Z型变压器的相关参数见表1，架空线路和电缆线路的相关参数见表2。

利用图4模型模拟不同故障位置F（=1,2,…, 18），如故障位置F1位于节点1和节点2之间，故障位置F2位于节点2和节点3之间，以此类推，故障依次沿着节点之间的连接路径发生。将仿真得到的数据分为历史样本和测试样本，历史样本用于生成两个聚类中心，样本参数见表3，各有180组数据。其中，为故障角。

典型故障样本参数及测试结果见表4，结果表明选段完全正确，说明仿真数据的故障区段和健全区段特征向量间存在显著差异，K均值聚类算法能够准确识别区段类型。

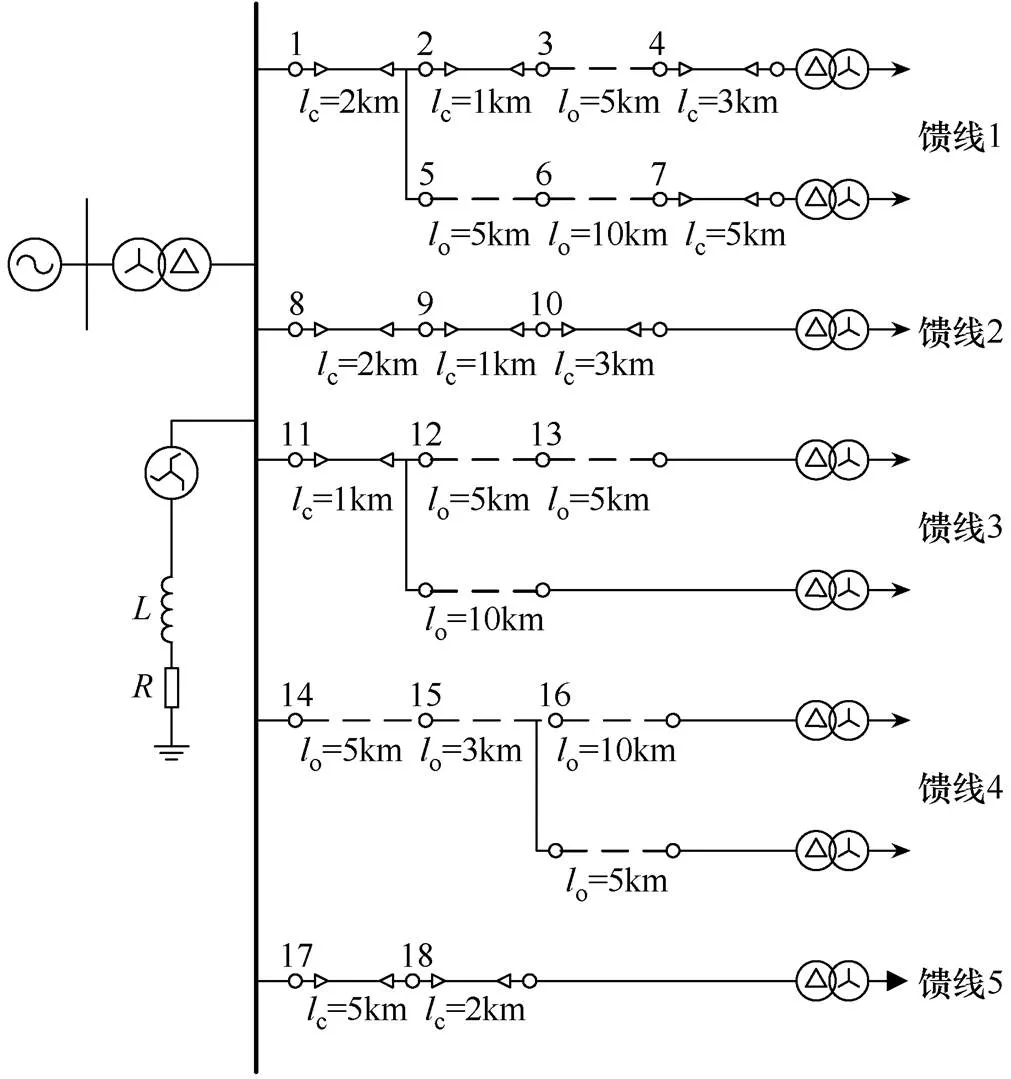
图4 10kV谐振接地系统仿真模型

表1 变压器参数

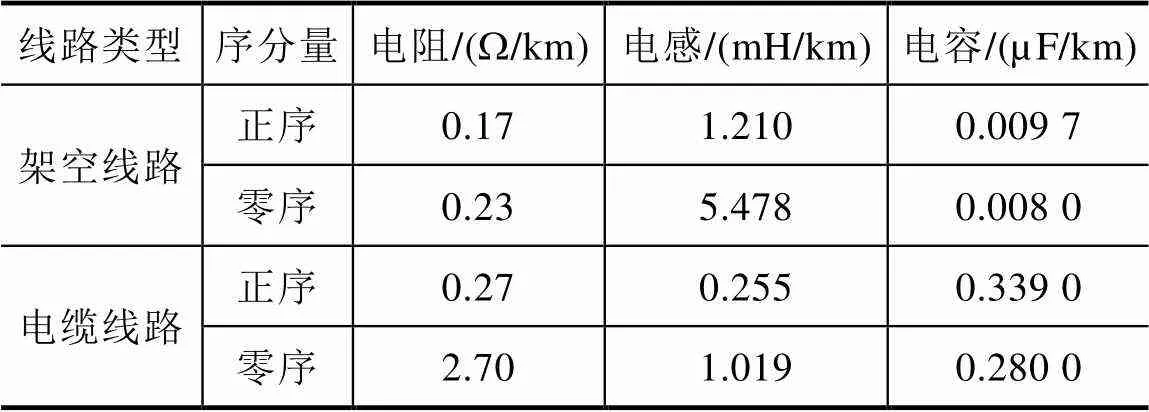
表2 线路参数

表3 历史样本和测试样本参数

表4 典型故障样本参数及测试结果

发生高阻接地故障时，由于故障信号微弱，容易导致选段错误。对高阻接地故障进行仿真，当故障位于F3时，选择两个故障区段和两个健全区段的数据，其三相电流变化量波形如图5所示，相应故障特征量见表5。

图5 高阻接地故障的三相电流变化量波形

表5 高阻接地故障的故障特征量

由图5可知，在故障区段，故障相与非故障相波形有较大差异，因此余弦相似度较小，偏移系数、奇异值和欧氏距离都较大；在健全区段，三相波形相似，因此故障特征向量的大小与故障区段刚好 相反。

3.2 实时数字仿真系统仿真

基于实时数字仿真系统（real time digital simulation system, RTDS）搭建的谐振接地系统仿真模型如图6所示，该系统包括8个节点，采样频率为10kHz，相关参数见表2。

利用该模型模拟12次单相接地故障，获得42组故障数据，仿真数据样本参数见表6。

当故障位于F2时，选择两个故障区段和健全区段的数据，其RTDS仿真的三相电流变化量波形如图7所示。与PSCAD/EMTDC软件的仿真波形相比，RTDS仿真波形不够平滑，但仍有类似的规律。

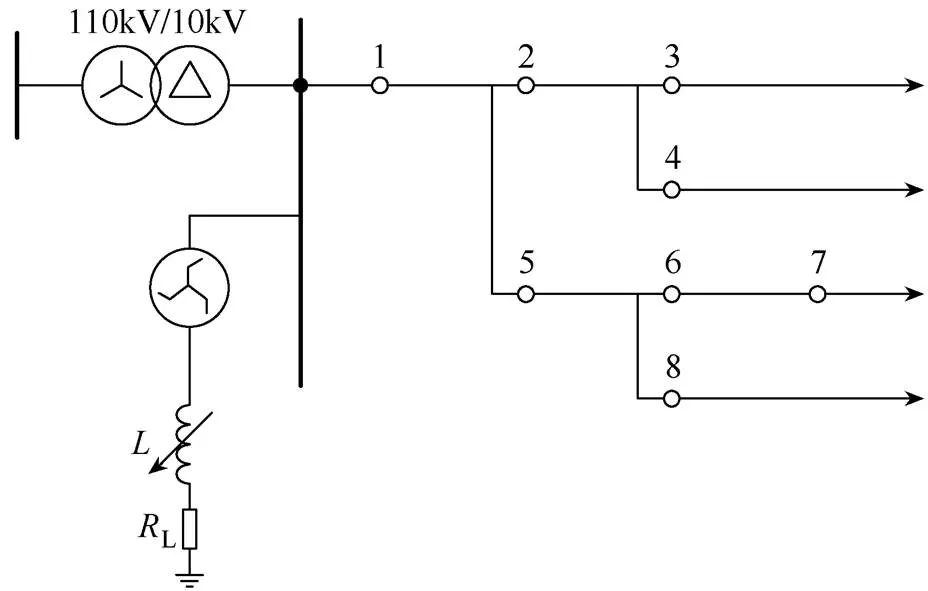
图6 谐振接地系统RTDS仿真模型

表6 RTDS仿真数据样本参数

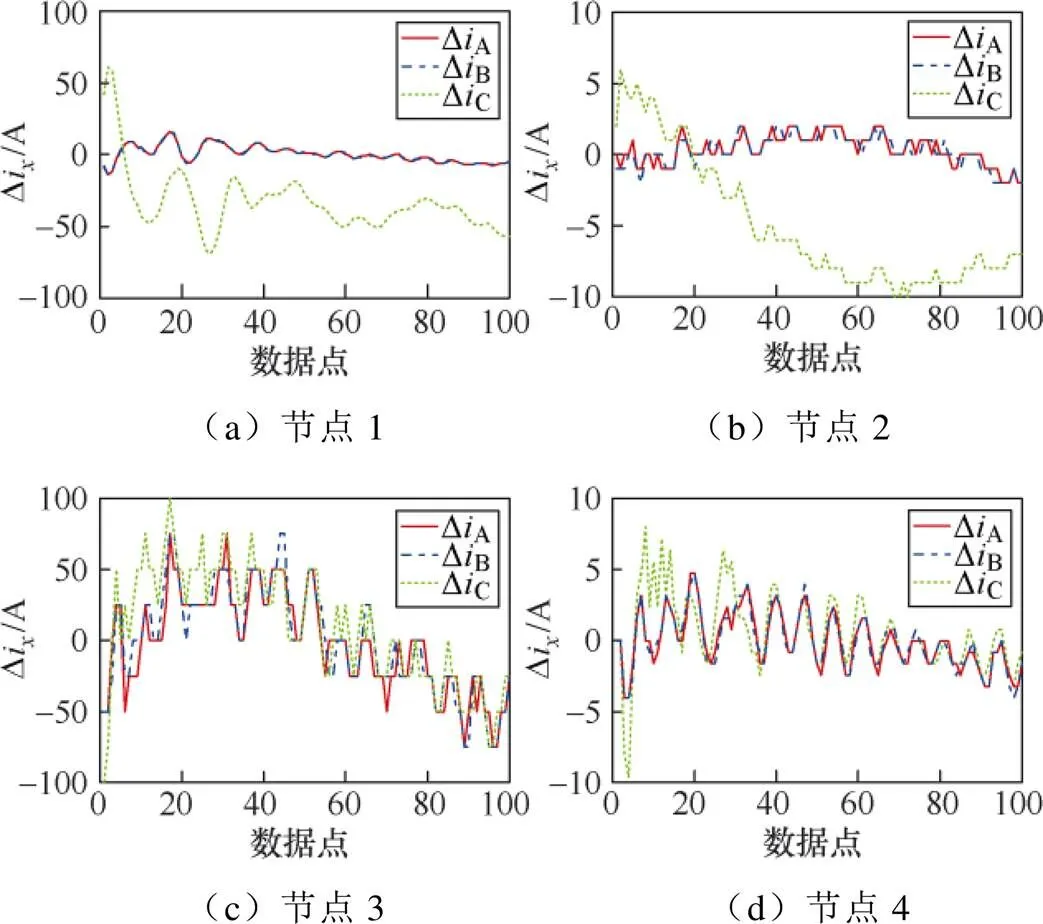
图7 RTDS仿真的三相电流变化量波形

从这4个检测节点的波形数据中提取4个故障特征量见表7。可以看出，故障区段和健全区段的余弦相似度、偏移系数、奇异值和欧氏距离都表现出较大的差异。

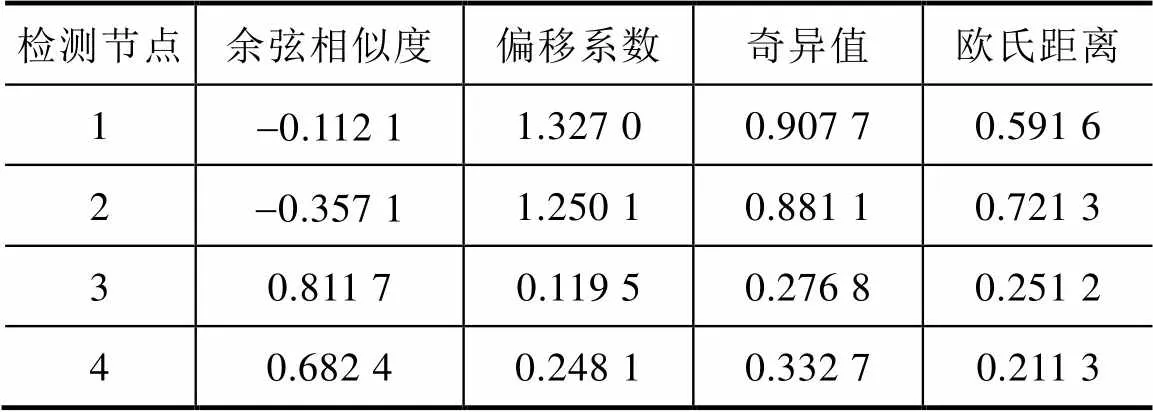
表7 RTDS仿真数据的故障特征量

将42组RTDS故障数据全部作为输入进行测试，历史样本同样来自RTDS仿真数据，测试结果见表8，准确率达到97.62%。以表3的历史样本输入RTDS进行测试时，准确率则下降至90.48%。结果表明，历史数据对K均值聚类算法的识别效果有很大影响，因此需要着重研究如何选择历史数据。

表8 RTDS仿真数据测试结果

3.3 现场数据验证

某10kV配电网结构如图8所示，该系统包括14个节点，采样频率为4kHz，获得3组故障案例，共22个故障样本。

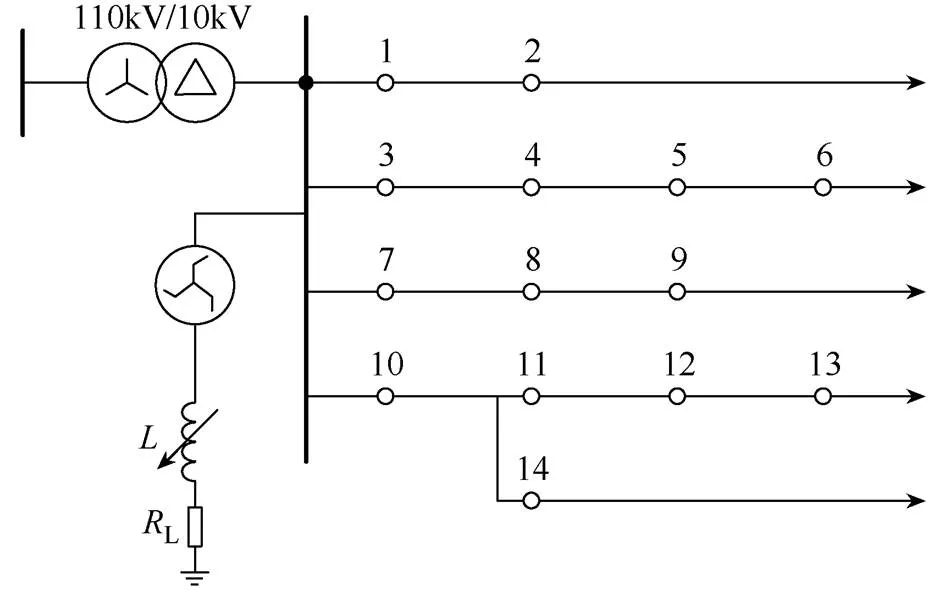
图8 10kV配电网结构

当故障位于F4时，选择两个故障区段和健全区段的数据，其三相电流变化量波形如图9所示。可以看出，与仿真波形相比，现场波形更加不规则，且由于噪声、三相参数不对称等因素的影响，故障特征更不明显，具体表现为：在故障区段，故障相与非故障相波形之间的差异减小，而非故障相波形之间的差异增大；在健全区段，三相波形之间的差异增大，提高了故障选段的难度。

图9 现场的三相电流变化量波形

从这4个检测节点的波形数据中提取4个故障特征量见表9。可以看出，虽然故障区段的偏移系数、奇异值和欧氏距离均比仿真小，但是仍与健全区段存在明显不同；故障区段的余弦相似度比健全区段小很多。

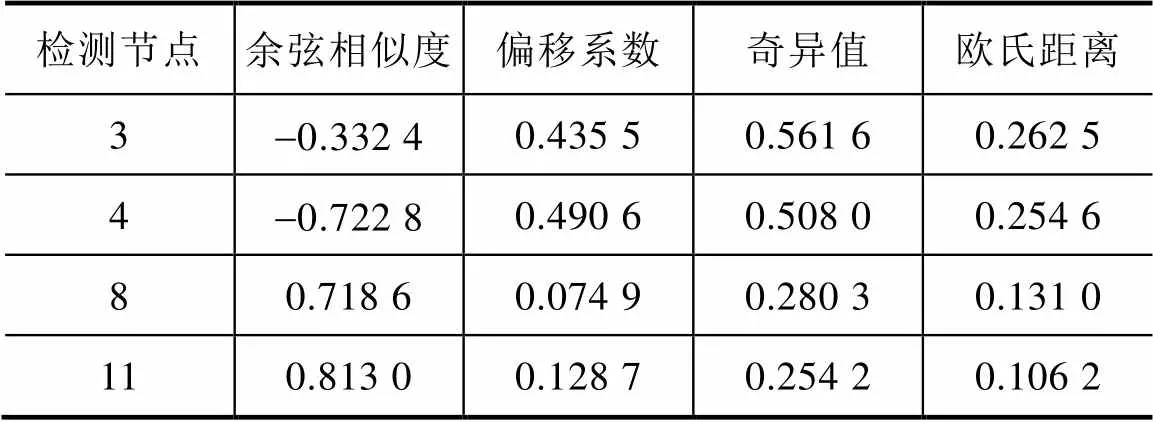
表9 现场数据的故障特征量

将现场数据输入K均值聚类算法进行测试，测试结果见表10，准确率达到90.91%。以表3的历史样本输入现场数据进行测试时，准确率下降至80.81%，说明在使用仿真模型时，需要考虑仿真数据和现场数据的潜在差异。

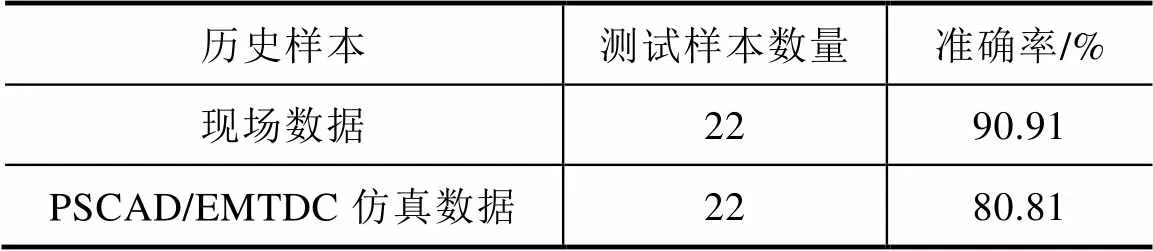
表10 现场数据测试结果

现场数据测试结果表明，本文所提选段方法能够较准确地识别现场数据。在后续研究中，需要更多地关注历史样本的选取，可将多种数据进行深度结合来提高选段方法对故障样本的识别能力。

4 结论

基于智能开关在配电网中的应用，本文提出了一种就地选段新方法，通过研究三相电流变化量波形特点，构建了包含余弦相似度、偏移系数、奇异值和欧氏距离的4维故障特征向量，将其输入K均值聚类算法进行区段定位。该方法无需训练或设置阈值，各智能开关仅需本区段数据，不用与主站通信。仿真和现场数据的测试结果表明，该方法具有较高的可靠性和适应性。

[1] 邓丰, 徐帆, 曾哲, 等. 基于多源暂态信息融合的单端故障定位方法[J]. 电工技术学报, 2022, 37(13): 3201-3212.

[2] 欧逸哲, 术茜. 基于SOM和K均值聚类的谐振接地系统故障选线及区段定位方法[J]. 电气技术, 2023, 24(10): 23-30.

[3] 王晓卫, 刘伟博, 郭亮, 等. 基于不同时段内积投影的灵活接地系统高阻故障选线方法[J]. 电工技术学报, 2024, 39(1): 154-167.

[4] 郭谋发. 配电网单相接地故障人工智能选线[M]. 北京: 中国水利水电出版社, 2020.

[5] 梁睿, 靳征, 王崇林, 等. 行波时频复合分析的配电网故障定位研究[J]. 中国电机工程学报, 2013, 33(28): 130-136.

[6] 李泽文, 刘基典, 席燕辉, 等. 基于暂态波形相关性的配电网故障定位方法[J]. 电力系统自动化, 2020, 44(21): 72-79.

[7] WANG Xiaowei, GAO Jie, WEI Xiangxiang, et al. Single line to ground fault detection in a non- effectively grounded distribution network[J]. IEEE Transactions on Power Delivery, 2018, 33(6): 3173- 3186.

[8] GU J C, HUANG Z J, WANG Jingmin, et al. High impedance fault detection in overhead distribution feeders using a DSP-based feeder terminal unit[J]. IEEE Transactions on Industry Applications, 2021, 57(1): 179-186.

[9] BARIK M A, GARGOOM A, MAHMUD M A, et al. A decentralized fault detection technique for detecting single phase to ground faults in power distribution systems with resonant grounding[J]. IEEE Transa- ctions on Power Delivery, 2018, 33(5): 2462-2473.

[10] 孙换春, 徐逸群. 高可靠性配网一二次融合技术[J]. 电工技术, 2020(1): 1-2.

[11] 喻锟, 胥鹏博, 曾祥君, 等. 基于模糊测度融合诊断的配电网接地故障选线[J]. 电工技术学报, 2022, 37(3): 623-633.

[12] 王康, 高伟, 杨耿杰. 基于高频分量的配电网高阻接地故障识别[J]. 电气技术, 2022, 23(2): 61-66, 87.

[13] GUO Moufa, ZENG Xiaodan, CHENG Duanyu, et al. Deep-learning-based earth fault detection using continuous wavelet transform and convolutional neural network in resonant grounding distribution systems[J]. IEEE Sensors Journal, 2018, 18(3): 1291-1300.

[14] 刘谋海, 王媛媛, 曾祥君, 等. 基于暂态相电流特征分析的故障选线新方法[J]. 电力系统及其自动化学报, 2017, 29(1): 30-36.

[15] 齐郑, 赵昕一, 陈艳波. 暂态与稳态相不对称信号相结合的配电网单相接地故障感知技术[J]. 高电压技术, 2022, 48(4): 1264-1276.

[16] 何乐彰, 何炳源, 徐俊杰, 等. 计及可靠性约束的配电网故障指示器优化布点方法[J]. 电力系统自动化, 2020, 44(18): 116-123.

[17] FARAJOLLAHI M, FOTUHI-FIRUZABAD M, SAFDARIAN A. Simultaneous placement of fault indicator and sectionalizing switch in distribution networks[J]. IEEE Transactions on Smart Grid, 2019, 10(2): 2278-2287.

[18] 林骏捷, 林佳壕, 郭谋发. 基于多暂态特征量聚类的配电网接地故障区段定位方法[J]. 电气技术, 2023, 24(5): 16-22.

Fault section location method in resonant grounding systems based on K-means clustering algorithm

HUANG Jie WANG Yifan LIN Yeqing HU Lidan WANG Danhao

(Fuzhou Power Supply Company, State Grid Fujian Electric Power Co., Ltd, Fuzhou 350004)

The current fault location method for resonant grounding distribution networks faces challenges such as excessive communication dependence, complex feature analysis, and difficulties in setting thresholds, resulting in reduced applicability for on-site operation. By studying the characteristics of three-phase current waveform variations, this paper, based on the deep integration of intelligent switches in distribution networks, introduces a local section selection method using the K-means clustering algorithm. This method extracts fault feature parameters, combining the advantages of unsupervised learning through the K-means clustering algorithm to identify section types. This approach allows each detection node to process only local fault signals, reducing the communication burden. The feasibility of this method is validated using both simulation and on-site data. Experimental results demonstrate that this method exhibits high reliability across various fault conditions and can effectively adapt to real-world environments.

resonant grounding system; single line to ground fault; local section selection; K-means clustering; unsupervised learning

国网福建省电力有限公司科学技术项目（521310230004）

2023-11-14

2023-11-24

黄 劼（1980—），男，福建长乐人，高级工程师，主要从事配电网调度自动化运行管理工作。