用于自动化仓库货位分配模式改进的数学模型设计

文/韦银幕 农建诚 蓝欢玉

1.自动化仓库货位分配模式改进数学模型设计

1.1 自动化仓库货位分配影响因素分析

仓库中货物空间的分配主要基于随机分配策略，重点考虑存储场所的精准匹配。利用空间分配算法建立了货物空间分配的优化方法。出于便于计算的目的，假设：

（1）仓库中的三个维度只有一个入口和出口点，每个巷道线宽都是协调一致的。（2）货物储存在托盘单元中，托盘单元形状是一个规则的矩形，重心位于其几何中心。

设货架层向集合为Q，且q∈Q；货架列向集合为S，且；存放货物的立体仓库的货架排向集合为R，且r∈R。共布置有ζR排货架在该立体仓库中，每排货架含ζs列∂Q层；设置（xrsq，yrsq，zrsq）为第r排第s列第q层的货位中心坐标（0，0，0）：仓库出入口坐标（0，0，0），第1排、第1列、第1层货架被规定为距离出入口最近的排、列、层。w0为巷道的宽度；，ls为第s列货架的长度，wr为第r排货架的深度，hq为第q层货架的高度，ψrsq为其货位位置；（ai，bi，ci）表示第i件货物的长宽高，周转率为pi，重量为gi，仓库内储存的货物集合用I来表示，i∈I。存储环境的位置临界值为ψi。当货物储存要求所需位置与实际储存位置精确一致时，应精确计算仓库中每个储存位置的实际位置。计算过程如下：

首先，在立体货架上，第r排第s列第q层的货位与所有位置计距离的集合用Drsq表示。将距离从最小到最大进行排序，然后使用货物位置中心附近的前一个位置计算货物的位置。在此计算的基础上，根据公式（1）确定负载位置中心与最近的仪表之间的距离d，drus∈Drsq。

其次，将两点之间位置的影响因素设定为两点之间位置差与两点之间距离的比值，并将从指定位置开始的位置的变化系数设置为所选m个位置之间m-1位置的平均影响因素。两个位置之间的距离d（ue，un）由公式（2）计算，位置的影响因素kue由公式（3）确定。

然后，结合位置与货位之间的距离drsq位置示数ψue以及位置变化系数kue，货位位置估计值按式(4）计算确定。

选取自动化仓库货位分配中影响因素评分排名较高的影响因素，作为优化变量代入改进数学模型中，用于进一步选取指标计算。

1.2 选取自动化仓库货位分配指标

为了实现自动化仓库货位分配数学模型的算法改进，在上述计算的基础上，在DATE系统中执行以下操作，选取自动化仓库货位分配指标：输入：相关货物、货物位置和位置数据。结果：优化后货运分配指标，得出目标函数值并终止迭代次数。步骤1：计算存储位置和进出口之间的距离，以及立体存储中所有存储中心的位置值，确定算法的性能参数和合规函数，根据存储位置编码规则创建初始分配指标N，每个初始分配指标应包括与限制M 相对应的分配指标。步骤2：在轮盘选择机制的基础上，从子分配指标中进行选择。随机数[0，1]是随机的，如果其数量小于1，则选择第一个存储站点分布方案。如果此数量大于1，选择第n个存储位置分配指标。重复选择N次，转步骤3，确保可用存储空间分配指标的数量不发生变化。步骤3：调整后的横交叉操作在步骤2中将所选择的分配指标在每个子组中两两配对，并且基于在每个分配指标中计算的一致性和使用最大横交叉操作和最小横交叉操作参数的选择操作的总一致性。如果数字小于1，则转入步骤4，如果数字大于1，则转入步骤6。步骤4：交叉操作，根据货物位置的部分协调和交叉操作、碰撞检测和映射关系处理规则，选择和转换货物。货位方案互换，以获得两个新的子代货物分配指标。步骤5：交叉操作合法性的确定，确定交叉操作后货物分配指标的大小和限制是根据约束条件进行判断的。如果同时满足尺寸和位置限制，则转入步骤6，否则转入步骤4，重新执行步骤4交叉操作。步骤6：根据方程（9）计算每个子群中每个个体对应的突变率。在[0，1]范围内的随机数，若该数小于1，转入Step 7，否则转入Step 4。步骤7：突变操作，根据反突变规则，在货运配送计划中对货位分配指标中的部分货物调整其储存地点。步骤8：确定变异的合法性，对进行变异操作后的货位分配指标按照约束条件约束尺寸判断进行判断，定义变异操作后的位置分配指标。若满足约束条件进入步骤9，如果没有，返回步骤7。步骤9：每个子群完成货运分配计划的更新，形成一个新的子群并转步骤10。步骤10：结束时的判断，确保最佳个体在代数中的行为已达到代数中的最少保持代数，并在其到达后终止，以实现仓库货位分配指标选取。

1.3 建立自动化仓库货位分配改进的数学模型

依照上述流程计算测量人员根据货物的不同位置计算出的货物的平均货位估计值m，作为最终货物的位置值。通过计算公式（5）来确定货位位置。

分别根据公式（6）和（7）计算总出入库距离和总重心高度。

由于f1、f2不适用于相同的范围，因此对f1、f2根据方程（8）和（9）进行标准化。

表示将所有货物放置在离进出口最近的外部存储场地产生的进出口距离，

方程（9）是为了减少货物进入仓库和距离仓库出口之间的总距离，以及作为优化目标的货物重心的总高度，方程（10）至（12）是货物分配过程中的尺寸限制。货舱配额限制方案不会造成货物或货舱之间冲突的情况。

模型的约束条件如下：

优化模型中涉及的模型参数含义如表1所示。

表1 参数含义

2.实验论证

为了验证本文方法的优越性，将本文方法与传统方法1和传统方法2进行对比试验，对基于三种方法的货位分配移动距离进行对比。

2.1 实验准备

本次实验截取立体仓库某一时刻的库存状况，进行一次出库货位分配以及一次入库货位分配。并使用所有空货位和满货位存储设施作为实验解集。每个目标函数相互影响，相关存储站点和外部存储站点的分布具有多个目标函数，无法找到优化每个函数的解决方案。需要一个单一的目标位置来分配存储位置。因此，有必要将几个目标函数转换为一个目标函数，以获得唯一的最优解。在上述计算的基础上，考虑到三维仓库的实际状态、不同目标函数的重要性以及每个目标函数对最终结果的影响，对目标函数的权重设置如表2所示。

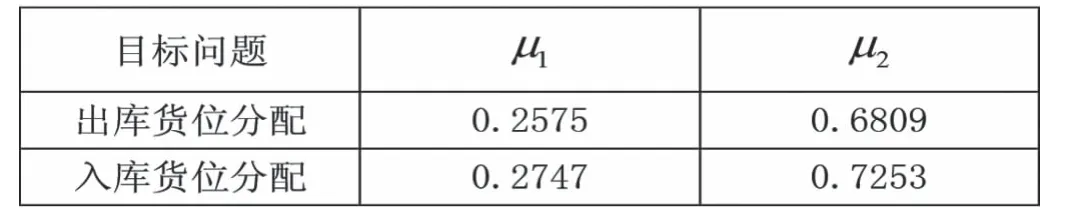
表2 目标权重设定表

具体实验结果对比如表3所示。

表3 三种方法货位分配移动距离

2.2 对比实验

根据表3数据可以得知，本文方法货位分配移动距离最短。比传统方法1平均缩短69.32米距离，比传统方法2平均缩短87.43米距离。通过对比实验可知，本文方法对于优化移动距离有一定提升。

3.结束语

综上所述，多品种小批量仓库包含多个小仓位，货物种类繁多，大量进出口货物存储的频率很高，存储运营的有效性已成为企业优化发展的重要目标。货运空间规划和分配是仓储工作的主要任务。文章以自动化仓库货位分配模式改进的数学模型设计为核心，探索了该模型在仓库管理中的应用过程，开发了一个仓库智能化模型，可以帮助相关人员按照标准的仓库管理要求从仓库中获取数据。