考虑电池寿命的电动物流车充电桩选址－路径优化

文/王彦冬

电动汽车作为一种新能源交通工具，已经被广泛地应用于各种物流场景。但是，现在仍有许多问题制约着电动汽车在物流配送领域的发展。多数学者是在有限地电池续航里程内进行路径优化或设施位置布局研究，或同时考虑两者。同时基于传统车辆路径问题研究的基础上，对EVRP进行了扩展，例如：考虑了容量加载约束[1]、客户满意度[2]、多车型电动汽车[3]、多车场、换电池模式、多类型充电桩、充电桩选址[4]等。现有研究旨在优化电动车辆的路径或是充电桩的选址，有学者对选址路径优化联合研究也没有考虑到电动车电池寿命对成本的影响。因此，针对电动物流车充电桩的选址－路径优化问题，本文将影响电池寿命的参数加入模型当中，提出了考虑电池寿命的电动物流车充电桩选址－路径优化问题，建立了该问题的整数规划模型，并设计带邻域搜索的遗传算法对其求解。最后，通过一个算例对模型和算法进行了测试和分析，证明了其有效性。

1.问题描述

本节构建了考虑电池寿命的电动物流车充电设施选址路径优化模型。具体问题可描述如下：某一物流企业有一个物流中心，需要使用电动物流车给N个客户配送货物，对于每个客户i都有对应的需求量qi和要求到达、离开的时间窗[ei，li]。如果电动物流车早于时间窗到达或者晚于时间窗离开都会支付相应的损失成本。每辆车均从配送中心出发，完成配送任务后返回配送中心。电动物流车的电池电量有限，在剩余电量不能到达下一个客户点时会选择相应的充电桩进行充电，同时，电动物流车在充电和行驶的过程中都会对电池造成损耗，降低电池寿命，增加成本。因此，要选择合适的位置建设充电桩并且规划电动物流车辆路径，使车辆能够完成配送任务并且让物流企业的总运营成本最小。本文考虑的客户点都是比较固定的，因此本文的充电桩选址是物流企业的长期决策。

2.模型建立

2.1 符号定义

充电桩选址－路径优化问题的变量定义如表2-1所示。

表2 -1 符号定义

2.2 模型构建

式（1）表示物流企业的总运营成本的最小值，包括：电动物流车的行驶成本、充电电池损耗成本、放电电池损耗成本、充电时间成本、电动物流车固定成本、充电桩购买成本和时间窗成本；式（2）表示充电造成的电池损耗成本；式（3）表示放电造成的电池损耗成本；约束（4）表示每个客户都被服务只被服务一次；约束（5）表示每辆车只使用一次；约束（6）表示保证了每辆车到达节点的次数与离开该节点的次数相同；约束（7）表示每辆车从配送中心出发完成任务后回到配送中心；约束（8）表示使用的电动物流车数量小于物流企业拥有的电动物流车数量；约束（9）表示电动物流车剩余的载货量；约束（10）表示电动物流车的最大载货量满足每条路径的需求量之和；约束（11）表示电动物流车在各点的电量；约束（12）表示电动物流车驶离充电桩后的车辆剩余电量；约束（13）表示电动物流车在充电桩的充电量为非负数，且充电后的电量小于等于电池最大容量；约束（14）表示电动物流车从配送中心出发时是满电状态；约束（15）表示电动物流车到达客户点和离开客户点时的电量不变；约束（16）表示电动物流车的电量能够满足剩余的配送任务；约束（17）表示如果电动物流车早于时间窗到达客户点时的等待时间；约束（18-20）表示电动物流车从离开节点到离开节点所使用的时间；约束（21）表示造成电池寿命降低的损耗历程所消耗的电量；约束（22）表示变量属性。

3.算法设计

针对电动物流车充电桩选址－路径优化问题，设计带领域搜索的遗传算法进行求解。算法具体流程如下：

3.1 编码设计。本文采用在遗传算法中加入变邻域搜索操作进行问题求解，应用混合整数编码的方式将一个可行解用客户、配送中心和充电桩共同编码来表示。

3.2 种群初始化。本文通过随机生成数列作为初始染色体，然后根据车辆负载和电池剩余容量等约束，使用插入充电桩等方式，对初始染色体分配车辆，生成一条符合配送需求的染色体。

3.3 适应度函数。适应度函数是用来计算染色体个体的适应度值，来判断个体的优劣。具体的计算公式如（23）所示

3.4 遗传操作

3.4.1 选择操作。本文根据初始种群中的每个个体的适应度值的大小，采用锦标赛策略进行父代个体的选择。使用锦标赛策略的优势在于，适应度值最大的个体，肯定会被选择成为父代，而适应度值越大的个体，被选中的概率就越大。

3.4.2 交叉操作。本文采用了子路径交叉的方式对染色体进行操作，表现为随机选择两个优秀的父代个体进行两两交叉。

3.4.3 变异操作。本文中的变异是采用Insert插入的方式来实现。具体操作如下：选择一个待变异的父代个体，随机生成两个染色体基因内的自然数x1和x2，在父代个体中删除x1，在x2+1的位置放入x1，形成新的子代。

3.4.4 VND邻域搜索。因为遗传算法本身具有良好的全局搜索能力，但是局部搜索能力较差，这就造成了其大多数情况下只能确定局部最优但是很少情况下会达到全局最优。所以本文在遗传算法的基础上，引入邻域搜索算法，邻域搜索算法的优点就是避免种群陷入局部最优，在达到局部最优时进行跳跃，在新的领域中生成后代，寻找全局最优解。本文引入了三种邻域搜索算子，分别是swap算子、2-opt算子和or-opt算子。这里只介绍2-opt算子。2-opt算子的操作如下：在遗传算法完成一次迭代后，取出此次迭代的最优个体，在个体中随机选择两个基因，将两个基因内的染色体顺序进行调换，形成新的染色体。比较新旧染色体的个体适应度值，保存适应度值较小的个体。

3.5 终止条件。当条件满足循环代数等于maxgen或满足连续30代种群中最优个体不变则终止遗传循环。

4.算例及结果分析

4.1 算例数据。为了验证本文建立模型的有效性和算法的能力，算例是包含1个配送中心，60个客户点，6个充电桩备选点，共67个节点的配送系统，有5辆电动物流车可提供配送服务。配送中心坐标为（35，35），具体数据见表4-1，遗传算法涉及参数设置如下：初始种群为300，迭代次数为500，交叉概率为0.9，变异概率为0.1。

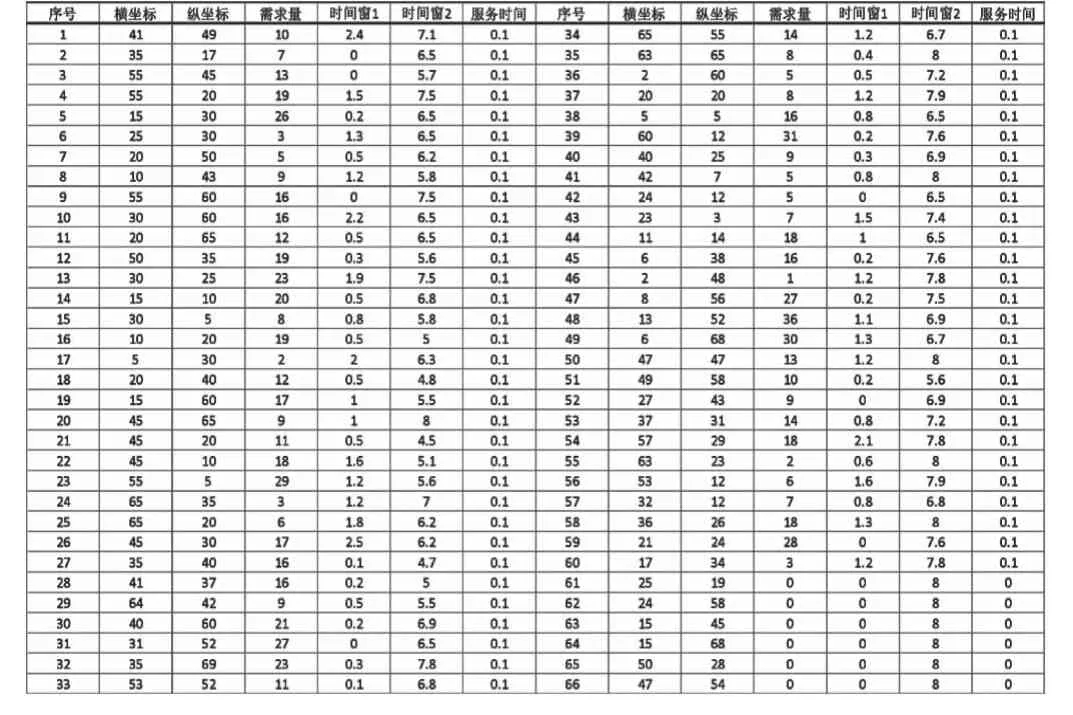
表4-1 节点详细信息

4.2 电动物流车充电桩选址路径－优化方案。考虑电池损耗的情况下，采用带邻域搜索的遗传算法对电动物流车充电桩选址路径－优化问题进行求解，运算结果如表4-2所示。

表4-2 配送路径及充电位置

4.3 结果对比分析。由表4-3可知，电动物流车行驶成本、电池损耗成本、充电成本均有所下降，总成本比模型二低了469.2027元。总成本节约了14.53%。充电成本节省了128.24%，电池损耗成本节省了141.54%。

表4-3 模型优化结果

结束语

本文在现有研究的基础上，以物流企业为研究对象，分别考虑了充、放电对电池寿命的影响，针对问题建立了相应的数学模型，统筹安排充电桩的选址位置和电动物流车的行驶路径，通过不同的优化策略，使得物流企业的总运营成本最低。同时，还设计了一种求解该问题的带邻域搜索的遗传算法。算例结果表明，考虑电池寿命和充电策略的电动物流车充电桩选址路径优化模型可以大幅降低电动物流车的电池损耗成本和充电时间成本，增加电动物流车电池寿命，达到降低运营成本的目的。