基于智能集成模型前胡切片微波真空干燥过程水分比预测
2024-04-09胡轶娟梁卫青童晔玲楼柯浪浦锦宝
胡轶娟 ,梁卫青 ,徐 攀 ,童晔玲 ,楼柯浪 ,浦锦宝 *
1.浙江省中医药研究院,浙江 杭州 310007
2.浙江省中药新药研发重点实验室,浙江 杭州 310007
干燥是中药材产地加工的重要环节,也是中药材品质和药性形成的关键步骤[1]。采用适宜的干燥工艺不仅可以促使中药材药用部位所含水分减失至有利于运输、贮藏,还可促使药用部位中药效物质的最大保留、毒性成分的有效降低和化学成分间的相互转化等物理化学变化[2]。由于干燥对中药材含水率的影响将打破中药材内部化学成分和分子结构的动态平衡,导致其形态、微观结构和有效成分发生变化,因此,中药材干燥过程中水分扩散以及含水率变化规律是研究中药材最佳干燥工艺的关键之一[3]。同时,含水率作为中药材干燥过程终点判定的关键指标之一,干燥过程含水率的实时反馈也是及时调整干燥参数、调控干燥过程和改进现有干燥工艺的基础条件之一。通过建立中药材干燥过程模型,可以揭示中药材干燥过程水分迁移的数学规律,实现干燥过程的含水率预测[4]。
目前,中药材干燥过程含水率的建模方法可以分为回归分析和人工神经网络,其中回归分析是主要方法[5-12]。基于回归分析的中药材干燥过程含水率预测模型存在以下不足:首先基于不同干燥方法或不同干燥参数建立的模型存在差异,导致模型缺乏普适性;其次,中药材干燥过程的含水率变化具有显著的非线性和时变性,且干燥过程由多种参数共同控制、影响,特别是对一些采用新干燥工艺的干燥过程机理认识不充分,导致模型预测精度不佳。人工神经网络作为一种智能化建模方法,具有良好的并行处理和自适应能力,能较好地反映干燥工艺参数与物料含水率之间的复杂非线性、时变性关系等优点,目前,已被广泛用于建立各种物料干燥过程含水率预测模型,但在中药材的应用还偏少[13-23]。
人工神经网络作为一种经验建模方法,其“黑箱”特性导致网络结构和训练参数的选择带有一定的主观性,在实际应用中一般采用遍历试错法寻找最佳的网络结构。该方法的前提条件是单一神经网络能挖掘出干燥过程数据集中包含的所有有效信息,而其它备选神经网络都是多余的,但是干燥过程的非线性和时变性导致单一神经网络对于干燥过程特性的提取能力非常有限,不可避免地存在模型稳定性和预测精度不足的问题。另外,人工神经网络的“黑箱”特性还存在泛化性(模型的外推能力)不足的问题。
为了提高干燥过程含水率预测模型的稳定性、泛化性和预测精度,拟开展基于智能集成模型的前胡切片微波真空干燥过程水分比预测研究。首先,开展不同干燥条件(微波功率、切片厚度和干燥层数)下的前胡切片微波真空干燥实验,通过收集实验数据构建用于干燥过程含水率建模的原始数据集,然后提出一种基于集成学习和反向传播(back propagation,BP)神经网络的智能集成建模方法,最后,采用该建模方法建立前胡切片微波真空干燥过程的水分比预测模型,并进行模型应用。研究工作以期为前胡切片干燥过程优化与控制提供重要技术支持,并为建立其它中药材的类似模型提供重要参考。
1 仪器与材料
1.1 仪器
NJZ07-9B 型微波真空干燥系统,主要由微波发射系统、冷凝收集系统、真空系统和控制面板所组成,微波真空干燥室为内径40 cm、深度25 cm 的圆柱形容器,微波频率为2 455 MHz,南京杰全微波设备有限公司;DQ-103 型台式方形中药切片机,温岭林大机械有限公司;DHG-9240A 型电热恒温鼓风干燥箱,上海一恒科学仪器有限公司;JM-B20002型电子天平,精度0.01 g,余姚市纪铭称重校验设备有限公司。
1.2 材料
考虑到干燥过程含水率建模对干燥实验原料的一致性要求,该批前胡药材的获取方式如下:2022年1 月采用同一批种子播种于浙江省淳安县中药材种植基地的同一地块,且该地块周边没有前胡栽培,并于2023 年1 月集中采挖。所有样品均经浙江省中医药研究院浦锦宝研究员鉴定,为伞形科前胡属植物白花前胡PeucedanumpraeruptorumDunn 的根。挑选表皮无机械损伤、无腐烂的前胡新鲜药材放入纸箱,随时用于产地趁鲜干燥加工。
2 方法与结果
2.1 微波真空干燥
2.1.1 实验设计 采用单因素实验法研究不同干燥条件(微波功率、切片厚度和干燥层数)下前胡切片干燥过程的含水率变化,具体实验方案如表1 所示。
实验因素及水平的选择均以大量前期实验结果为基础。为了使前胡切片干燥过程含水率变化较为明显,并扩大含水率预测模型的适用范围,适当增加了前胡切片的厚度间距。由前期实验结果可知,随着真空度的增加,干燥时间略有缩短,但差异并不显著,且过大的真空度会导致静电释放、缩短微波管寿命,因此,所有干燥实验的真空度都固定为800 Pa。
微波真空干燥实验的操作步骤如下:取出新鲜前胡药材,采用流水冲洗前胡药材,除去须根,选取相同部位(主根直径为0.8~1.7 cm)洗净,清洗干净后放过夜阴干表面水分。根据切片的厚度要求对切片机进行相应设置,用切片机沿前胡药材横截面切成圆形薄片。每组实验的前胡切片质量为200 g乘以干燥层数。首先,根据设计好的实验方案,选取相应厚度并称取相应质量的前胡切片,然后将第一层切片均匀平铺在干燥室托盘中,确保切片尽量在上下表面进行传质,若摊铺多层则将新切片继续均匀平铺在下一层之上,最后设置好相应的微波功率进行微波真空干燥实验,干燥过程中切片均放置于干燥箱同一位置。
由于对真空状态的干燥实验进行取样称定质量会破坏干燥过程的连续性,直接影响前胡切片水分的表面蒸发、内部扩散过程,不能真实反映干燥过程的连续动态,会对采用干燥过程取样称定质量的方法获取的前胡切片含水率数据造成不利影响,因此,设计了以下实验操作步骤:首先设定一组干燥参数组合进行前胡切片微波真空干燥实验,干燥至5 min 时停止实验取出所有前胡切片进行离线称定质量、不再继续干燥,得到干燥至5 min 的前胡切片质量数据,然后重复相似操作,可以依次得到在该干燥参数组合下干燥至其他5 min 整数倍时间(例如:10、15、20 min)的前胡切片质量数据。在该组干燥参数组合实验中,若相邻5 min 内前胡切片的2 次质量数据之差约小于初始质量的1%,则完成该干燥参数组合的干燥实验,同时,将最后1次实验的所有前胡切片取出放于烘箱内105 ℃烘干5 h 得到前胡切片干物质(达到绝干状态)的质量数据。每组干燥参数组合的干燥实验均重复3 次,取平均值用于干燥过程的含水率变化规律分析和含水率建模。
2.1.2 水分比 前胡切片的干基含水率是指前胡切片在干燥过程中某一时刻的水分质量与前胡切片中干物质质量的比值。任意干燥t时刻前胡切片干基含水率(Mt)的计算公式如下[24]。
Mt=(mt-m0)/m0
mt表示任意干燥t时刻前胡切片的质量,m0表示前胡切片干物质的质量
采用水分比(moisture ratio,MR)表示前胡切片在不同时刻的含水率。任意干燥t时刻前胡切片水分比(MRt)的计算公式如下[25]。
MRt=Mt/M0
M0表示前胡切片的初始干基含水率
2.2 水分比智能集成建模
2.2.1 BP 神经网络设计 选择目前常用且性能良好的BP 神经网络作为子模型,用于建立前胡切片干燥过程水分比智能集成模型。BP 神经网络由输入层、隐含层和输出层所组成,其结构参数包括输入层神经元个数、输出层神经元个数和隐含层的层数(包括各隐含层的神经元个数)等。
选择微波功率、切片厚度、干燥层数和干燥时间作为输入层神经元,将不同干燥时刻的前胡切片水分比作为输出层神经元,即输入层的神经元个数为4,输出层的神经元个数为1。由于已有理论证实,BP 神经网络在不限制隐含层神经元个数的情况下,只需1 个隐含层,就可实现输入到输出的非线性映射[16]。同时考虑到模型复杂性和模型训练时间等因素,可以采用单隐含层。用于预测前胡切片干燥过程水分比的BP 神经网络拓扑结构如图1 所示。
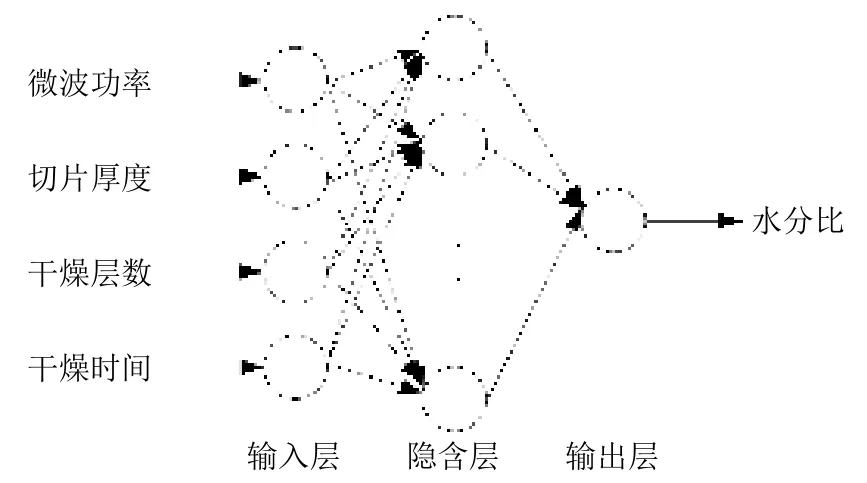
图1 用于预测前胡切片干燥过程水分比的BP 神经网络拓扑结构Fig.1 Topological structure of BP neural network for predicting moisture ratio of Peucedani Radix slices during drying process
隐含层的神经元个数设置对神经网络的性能影响较大,过多会导致网络复杂度增加、网络训练时间多长,过少则会导致生成的连接权组合个数不够、难以满足样本的学习要求。一般采用以下经验公式确定隐含层的神经元个数(l)[16]。
l=(p+q)1/2+a
p为输入层的神经元个数,q为输出层的神经元个数,a为1~10 的常数
等确定BP 神经网络的结构参数以后,还需要设置以下参数:输入层、隐含层与输出层之间的传递函数,网络训练函数,网络性能函数,最大训练次数和训练目标等[26-28]。为了大幅度降低编程工作量,采用MATLAB R2017b 软件的神经网络工具箱建立BP 神经网络模型。BP 神经网络的参数设置结果如表2 所示,表2 中的各种函数均为MATLAB软件神经网络工具箱中便于调用的内嵌函数。

表2 BP 神经网络的参数设置Table 2 Parameter setting of BP neural network
2.2.2 智能集成模型设计 集成学习是机器学习的一种重要方法,其设计思路是通过将一定数量且存在差异的基学习器进行组合,以提高单一学习器的稳定性和泛化性[29]。基于该设计思路可以设计一种基于集成学习和BP神经网络的智能集成建模方法,以提高模型的稳定性、泛化性和预测精度。
前胡切片微波真空干燥过程水分比智能集成模型结构如图2 所示。由图2 可知,该智能集成模型的水分比预测输出(MRint)按公式计算。
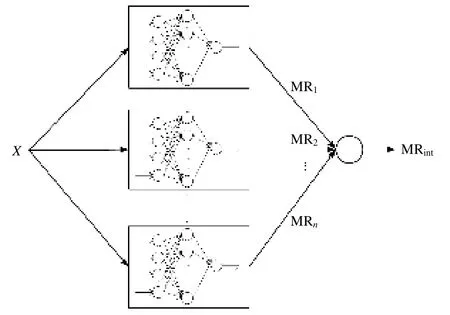
图2 前胡切片微波真空干燥过程水分比智能集成模型结构Fig.2 Structure of intelligent integrated model for moisture ratio of Peucedani Radix slices during microwave vacuum drying process
MRint=w1MR1+w2MR2+…+wnMRn
wi(i=1, 2, …,n)表示第i个BP 神经网络子模型的权重系数,MRi(i=1, 2, …,n)表示第i个BP 神经网络子模型的水分比预测输出,n表示用于集成的子模型总数
智能集成模型的建立流程包括集成方式选择与权重系数求取。集成方式可分为全集成和选择性集成,其中全集成是将所有神经网络子模型进行集成,选择性集成是选择部分神经网络子模型进行集成。当确定用于集成的BP 神经网络子模型规模以后,一般可以采用等权值法求取各子模型的权重系数,但考虑到各子模型之间的差异性,还可以采用熵值法。熵值法的设计思路是:若某子模型的预测误差序列变异程度越大,则其在集成模型中对应的权重系数就越小[30]。
第i个BP 神经网络子模型、第j个样本水分比预测值的变异系数采用预测相对残差(eij)表示。
Oij表示第i个BP 神经网络子模型、第j个样本的水分比预测输出,MRj表示第j个样本的水分比期望输出,j表示样本数目(j=1, 2, …,m),i表示BP 神经网络子模型数目(i=1, 2, …,n)
第i个BP 神经网络子模型的信息熵计算公式如下。
pij表示预测相对残差比重,Ei表示第i个BP 神经网络子模型的信息熵
各BP 神经网络子模型的权重系数wi计算公式如下。
2.2.3 实施流程 前胡切片微波真空干燥过程水分比智能集成建模的实施流程包括数据收集与分组、子模型建立、子模型集成和集成模型应用等,实施流程图如图3 所示。
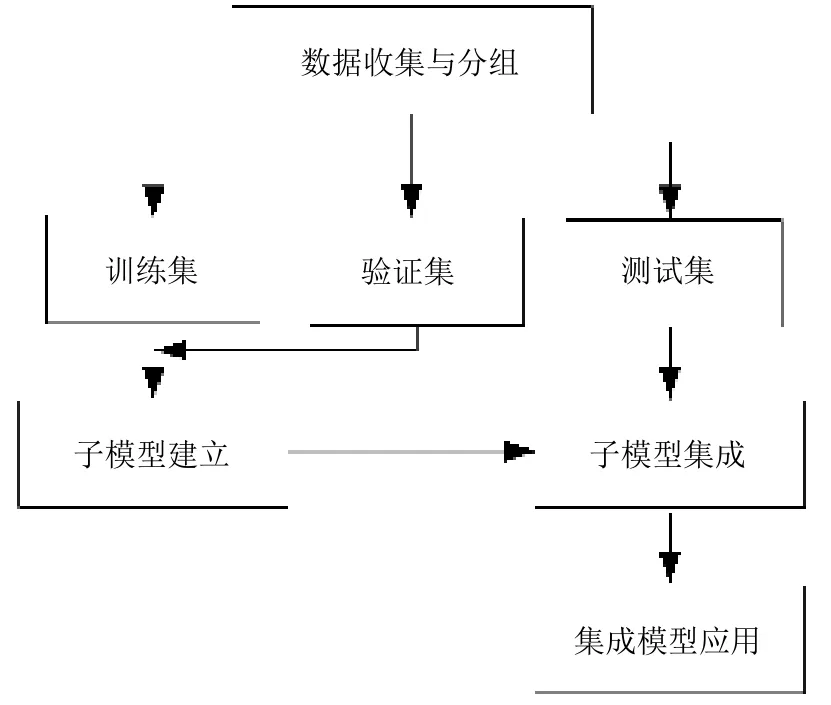
图3 前胡切片微波真空干燥过程水分比智能集成建模的实施流程Fig.3 Implementation process of intelligent integrated modeling for moisture ratio of Peucedani Radix slices during microwave vacuum drying process
(1)数据收集与分组:收集前胡切片微波真空干燥实验的所有实验数据构建原始数据集。为了避免输入输出数据的量纲和范围差异对模型训练带来不利影响(例如:tansig 函数饱和导致训练减慢或停止),在模型训练前需要先将输入和输出数据进行标准化处理,使其在[−1,1]范围内。
模型的泛化性是指根据有限样本得到的模型对新样本也具有良好的预测能力。为了提高模型的泛化性,将原始数据集合理划分为训练集、验证集和测试集,其中将表1 中序号为1、2、5、6、9、10的所有实验数据划分为训练集,表1 中序号为3、7、11 的所有实验数据划分为验证集,表1 中序号为4、8、12 的所有实验数据划分为测试集。
(2)子模型建立:按照表2 设置好模型参数,将标准化处理后的训练集输入BP 神经网络开展网络训练。当p=4 和q=1 时,BP 神经网络的隐含层神经元个数可以取3~12,由此可以采用训练集建立10 个BP 神经网络子模型。在BP 神经网络训练过程中,利用验证集、采用交叉验证方法避免模型的过拟合。
(3)子模型集成:当建立10 个BP 神经网络子模型以后,首先采用测试集得到所有子模型的评价指标数据,然后采用全集成方式将所有10 个子模型都用于集成,或者根据测试集的评价指标数据合理筛选用于集成的子模型,最后采用等权值法或熵值法求取各子模型(用于集成的)的权重系数,从而建立智能集成模型。
(4)集成模型应用:将建立的智能集成模型进行实际应用,一般是选取与实验方案差异较大的干燥参数组合。同时,还需要将智能集成模型的预测性能与所有子模型进行比较,以进一步验证智能集成模型的稳定性、泛化性和预测精度。
采用决定系数(R2)和均方根误差(RMSE)定量评价所有模型(包括子模型和智能集成模型)的预测性能。R2越接近于1,RMSE 越小,则表明模型的性能越佳。R2和RMSE 这2 个评价指标的具体计算公式分别如下[11]。
MRexp,i表示干燥实验得到的第i个水分比数据,MRpre,i表示各种模型计算得到的第i个水分比数据,N表示实验数据总数
3 结果与分析
3.1 干燥过程水分比变化规律
3.1.1 微波功率 根据表1 中序号1~4 的实验方案,可以得到当切片厚度为1 mm、干燥层数为1层时,不同微波功率下前胡切片水分比随干燥时间的变化曲线如图4 所示。当微波功率由300 W 逐渐升至600 W 时,总干燥时间由70 min 逐渐降至40 min。这是因为当微波功率增大,前胡切片内部水分吸收的微波能越多,可加速水分子间的摩擦和振动速度,更容易产生摩擦热,促进升温。同时,在真空环境下,水的汽化温度会因为蒸汽压的减小而降低,使得汽化速度加快,因此,提高微波功率可以提高失水速度、缩短干燥时间,从而提高干燥效率[31]。
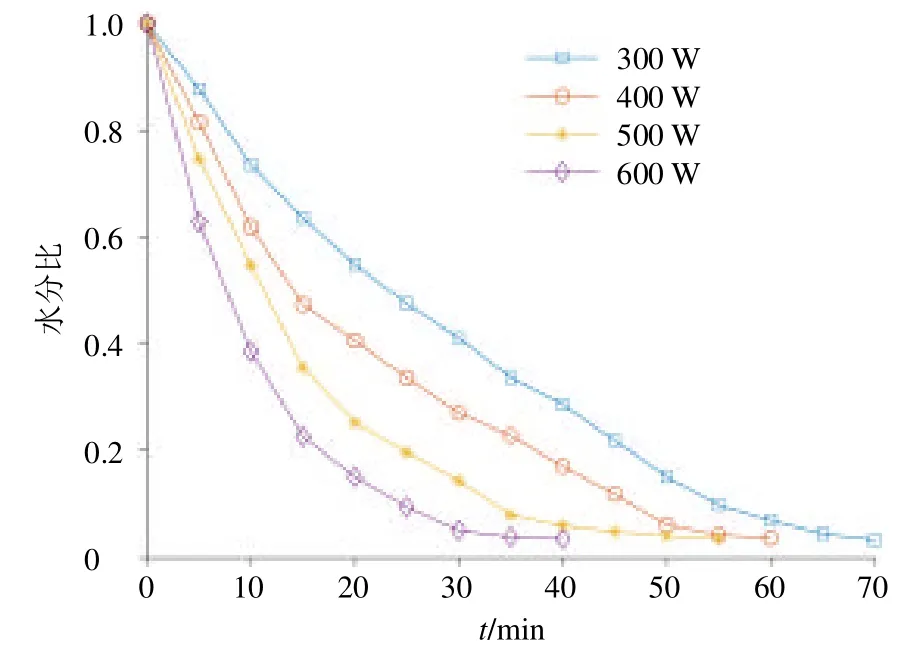
图4 不同微波功率下前胡切片水分比随干燥时间的变化曲线Fig.4 Moisture ratio curve of Peucedani Radix slices with drying time under different microwave power
3.1.2 切片厚度 根据表1 中序号5~8 的实验方案,可以得到当微波功率为400 W、干燥层数为2层时,不同切片厚度下前胡切片水分比随干燥时间的变化曲线如图5 所示。当切片厚度由7 mm 逐渐降至1 mm 时,总干燥时间由75 min 逐渐降至65 min。这是因为微波能量在前胡切片内部渗透过程中是不断衰减的,前胡切片厚度越薄,中心部分获得的微波能量越多,内部水分迁移扩散阻力越小,水分可以从切片内部更及时地迁移到其表面,然后蒸发去除,因此减少切片厚度可以缩短干燥时间[32]。
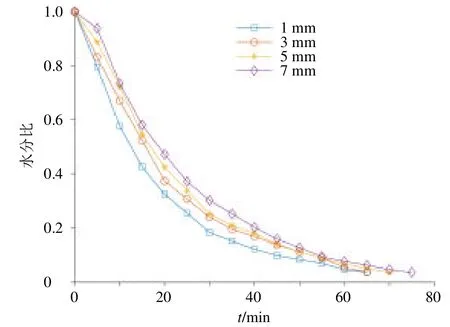
图5 不同切片厚度下前胡切片水分比随干燥时间的变化曲线Fig.5 Moisture ratio curve of Peucedani Radix slices with drying time under different slice thicknesses
3.1.3 干燥层数 根据表1 中序号9~12 的实验方案,可以得到当微波功率为600 W、切片厚度为3 mm 时,不同干燥层数下前胡切片水分比随干燥时间的变化曲线如图6 所示。
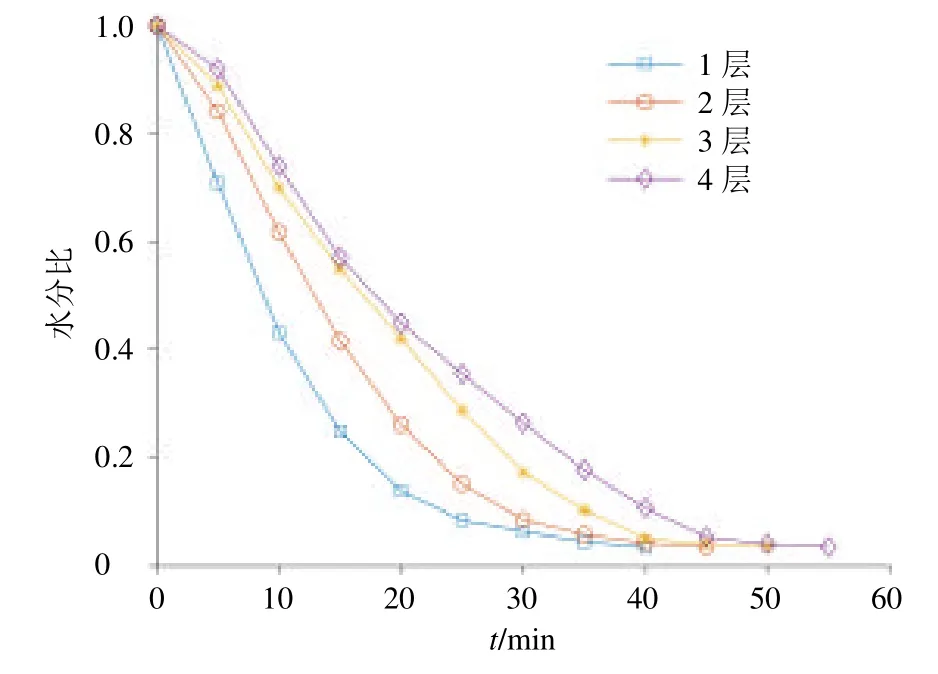
图6 不同干燥层数下前胡切片水分比随干燥时间的变化曲线Fig.6 Moisture ratio curve of Peucedani Radix slices with drying time under different drying layers
当干燥层数由4 层逐渐降至1 层时,总干燥时间由55 min 逐渐降至40 min。这是因为干燥层数越少,前胡切片中所需要去除的水分就相应地减少,单位质量前胡切片所吸收的微波能量相应地增加,同时干燥室内的气流可以更有效地循环,有利于去除前胡切片中的水分,因此,减少干燥层数可以缩短前胡切片的干燥时间[33-34]。
3.2 水分比智能集成建模与应用
3.2.1 子模型建立 通过开展前胡切片微波真空干燥实验,共收集得到150 组实验数据用于构建原始数据集。根据训练集、验证集和测试集的划分方法,训练集由75 组数据构成,验证集由38 组数据构成,测试集由37 组数据构成。
采用训练集建立了10 个BP 神经网络子模型,各子模型的隐含层神经元个数分别为3~12。以隐含层神经元个数3 为例,BP 神经网络训练过程的训练误差变化曲线如图7 所示。由于采用了交叉验证方法(有时也称为提前终止法),在训练初始阶段(训练次数小于17),随着训练次数的增加,训练集和验证集的均方误差(mean squared error,MSE)同时呈现下降趋势,此时属于网络的欠拟合阶段;等训练次数大于17 时,训练集的均方误差继续呈现下降趋势,而验证集的均方误差却呈现上升趋势,此时属于网络的过拟合阶段。当神经网络终止训练时,网络返回具有最小验证集误差(当训练次数等于17时)的权值和阈值。
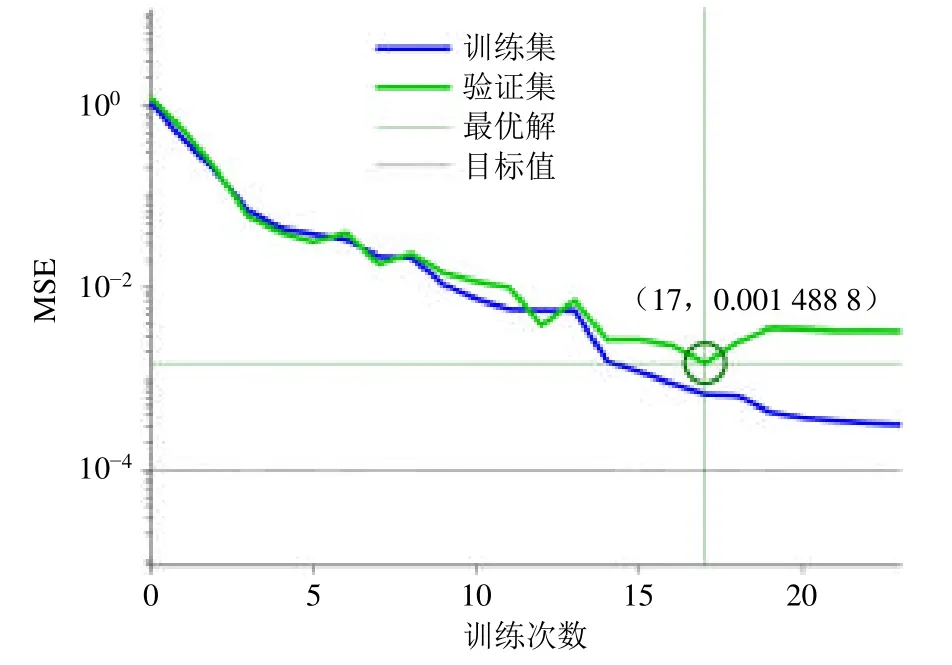
图7 BP 神经网络训练过程的训练误差变化曲线 (隐含层神经元个数为3)Fig.7 Training error curve of BP neural network training process (with three hidden layer neurons)
所有BP 神经网络子模型模型的性能指标数据(训练集和验证集)如表3 所示。不管是训练集还是验证集,所有BP 神经网络子模型的评价指标R2都大于0.96,这表明神经网络模型的训练效果是良好的,且不存在欠拟合状态,可以有效地表示输入端(微波功率、切片厚度、干燥层数和干燥时间)与输出端(前胡切片水分比)之间的非线性映射关系。

表3 所有BP 神经网络子模型的评价指标数据Table 3 Evaluation index data of all BP neural network submodels
由表3 还可知,对于不同隐含层神经元个数的BP 神经网络子模型,各模型的评价指标数据存在较大差异,且验证集的评价指标数据波动要大于训练集,这表明模型的稳定性较差。同时,对于相同隐含层神经元个数的BP 神经网络子模型,绝大多数的验证集评价指标数据要比训练集差。这是因为干燥过程的复杂性导致单一神经网络对于干燥过程特性的提取能力非常有限,单一神经网络无法较好地描述干燥过程的全局特性。与训练集相比,验证集属于模型外推的情形,验证集的评价指标数据表明单一神经网络存在稳定性和泛化性不足的问题。
3.2.2 子模型集成 将建立的10 个BP 神经网络子模型应用于测试集,各子模型的评价指标数据(测试集)如表3 所示。由于与验证集类似,测试集仍属于模型外推情形,因此,与训练集、验证集相比,测试集的所有子模型评价指标数据不仅要更差一点,而且还发生了更大波动,这进一步说明了单一神经网络模型存在稳定性和泛化性不足的问题。
除了采用全集成方式,将所有10 个子模型都用于集成,还根据测试集的评价指标数据,对子模型进行选择性集成。对于选择性集成,设置了R2>0.95作为优选条件,共优选得到5 个BP 神经网络子模型(神经元个数分别为3~5、7、11)用于模型集成。可采用等权值法或熵值法计算各子模型的权重系数。① 采用等权值法,全集成的各子模型权重系数均为0.1,选择性集成的各子模型权重系数均为0.2。② 采用熵值法计算得到全集成的各子模型权重系数(按照隐含层神经元个数从小到大)分别为w1=0.100,w2=0.102,w3=0.094,w4=0.098,w5=0.093,w6=0.098,w7=0.105,w8=0.106,w9=0.098,w10=0.106;选择性集成的各子模型权重系数(按照隐含层神经元个数从小到大)分别为w1=0.209,w2=0.216,w3=0.187,w4=0.183,w5=0.205。由熵值法的所有计算结果可知,各子模型的权重系数一般是0.1 附近(全集成)或0.2 附近(选择性集成),这表明各子模型差异性并不大。
根据集成方式和权重系数求取方法的不同,共建立了4 个前胡切片水分比智能集成模型,各智能集成模型的评价指标数据(测试集)如表4 所示。采用选择性集成方法建立的智能集成模型评价指标数据都优于全集成,但权重系数求取方法(等权值法和熵值法)对模型评价指标数据影响几乎一致,这可能是因为前胡切片水分比这个建模对象较为简单、无法完全体现熵值法的优势。通过对比表4(智能集成模型)与表3(子模型)的评价指标数据可知:选择性集成模型的性能要优于90%的子模型,且与最佳子模型(隐含层神经元个数为5)非常接近,这表明采用选择性集成方法建立的前胡切片水分比智能集成模型,具有良好的稳定性、泛化性和预测精度。
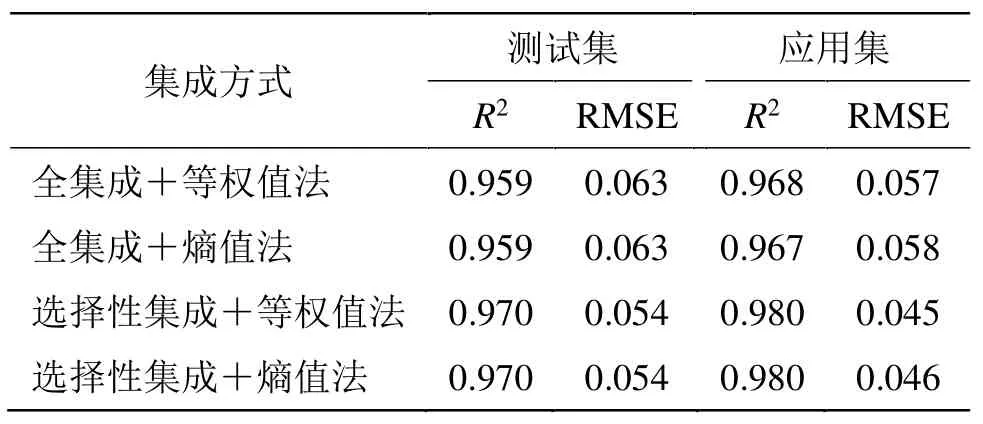
表4 所有智能集成模型的评价指标数据Table 4 Evaluation index data of all intelligent integrated models
3.2.3 集成模型应用 选取与实验方案差异较大的干燥参数组合,开展智能集成模型的应用工作,用于进一步验证前胡切片水分比智能集成模型的性能。原始数据集里已有干燥时间最短的干燥参数组合(微波功率为600 W,切片厚度为1 mm,干燥层数为1 层),这里选取干燥时间最长的干燥参数组合(微波功率为300 W,切片厚度为7 mm,干燥层数为4 层)。根据该干燥参数组合,按照相同的干燥步骤开展前胡切片微波真空干燥实验,将得到的实验数据作为应用集。
所有BP 神经网络子模型的评价指标数据(应用集)如表3 所示。由于应用集仍然属于模型外推情形,且子模型存在稳定性、泛化性不足的问题,导致应用集的所有子模型评价指标数据都发生了较大波动,且与表3 的测试集评价指标变化趋势较为吻合,即:对于相同的隐含层神经元个数,测试集的评价指标数据较差(例如:神经元个数为8 和10)或较好(例如:神经元个数为5 和11),则应用集的评价指标数据一般也较差或较好。
所有智能集成模型的评价指标数据(应用集)如表4 所示。4 种智能集成模型的评价指标数据差异较小,这表明智能集成模型的稳定性较好。同时,应用集仍属于模型外推情形,与表3 相比,表4 中选择性集成模型的性能要优于90%的子模型,且与最佳子模型(隐含层神经元个数为11)非常接近,这表明模型的泛化性较好。前胡切片水分比智能集成模型(选择性集成+熵值法)的应用集预测效果如图8 所示。
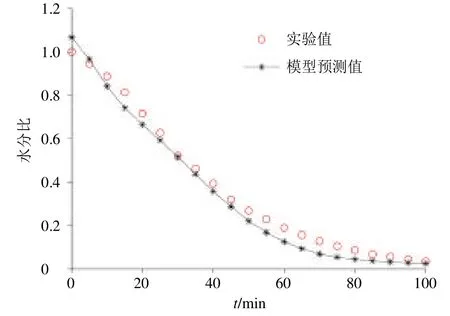
图8 前胡切片水分比智能集成模型 (选择性集成+熵值法) 的应用集预测效果Fig.8 Application set prediction effect of intelligent integrated model (selective integration and entropy method)for moisture ratio of Peucedani Radix slices
4 讨论
通过合理设计前胡切片微波真空干燥实验,探究了微波功率、切片厚度和干燥层数对前胡切片微波真空干燥过程水分比变化的影响。实验结果表明,提高微波功率或减少切片厚度都能够有效缩短总干燥时间,减少干燥过程真空泵的运行时间,达到提高干燥效率、节能的目的。与切片厚度、干燥层数相比,微波功率对总干燥时间的影响更为显著。同时,通过实验共收集了150 组包括干燥参数组合、干燥时间和水分比的实验数据,构建了用于前胡切片干燥过程水分比建模的原始数据集。另外,还收集了21 组实验数据用于进一步验证智能集成模型的稳定性、泛化性和预测精度。
为了克服单一BP 神经网络稳定性、泛化性和预测精度等不足的问题,提出了一种基于集成学习和BP 神经网络的智能集成建模方法,并通过子模型建立、子模型集成和集成模型应用等实施流程,建立了前胡切片干燥过程水分比的智能集成模型。该智能集成建模方法积极借鉴了集成学习的思想,通过合理集成多个不同隐含层神经元个数的BP 神经网络子模型,充分挖掘干燥过程数据中隐含的细节特征和高度非线性特征,减弱了单一模型的非线性程度,消除了单一模型的不确定性,在既保证各子模型相容性问题的同时,又保留了各子模型的差异性,能够较好地描述前胡切片干燥过程的全局特性。模型应用结果表明:智能集成模型具有较好的稳定性、泛化性和预测精度。
前胡切片干燥过程中水分比智能集成模型,较好地反映了微波真空干燥工艺参数与前胡切片水分比之间的复杂非线性关系,可以用于快速准确地预测干燥过程的水分比变化。另外,智能集成建模方法还为中药材干燥过程的建模提供了一种有效的建模新方法。研究结果不仅有助于准确掌握前胡切片干燥过程含水率的变化规律,还可以为前胡切片干燥过程优化和控制提供重要的技术支持,这对保证中药材干燥品质和降低能耗都具有重要的理论及现实意义。
前胡切片的品质评价不仅仅在于水分比这一指标,还应包括药材的性状(例如:颜色)、有效成分含量(例如:香豆素类成分含量)等诸多因素。笔者还开展了一些前胡切片微波真空干燥实验,用于研究干燥后前胡切片香豆素类成分含量变化,以及干燥过程前胡切片的色度变化,并得到了一些初步研究结果。香豆素类是前胡药材的主要有效成分,虽然这些成分相对较稳定,但是在干燥过程中也会发生不同程度的降解和转变[3]。由于微波真空干燥实验的温度变化范围为25.2~39.6 ℃,所有干燥条件(微波功率、切片厚度等)的变化对干燥后的前胡切片香豆素类成分含量影响均不显著,因此微波真空低温干燥技术可以减少香豆素类成分的损失,提高前胡切片的干燥品质。在微波真空干燥过程中,前胡切片由白逐渐变黑,由绿变红然后偏红程度逐渐保持稳定,由蓝变黄然后偏黄程度逐渐降低,总色差值逐渐增加。虽然增大微波功率可以缩短干燥时间,但会增加前胡切片的颜色劣变影响。今后可以在这些前期研究工作和本研究工作的基础上,进一步开展前胡切片微波真空干燥过程的质量综合评价、质量退化建模和工艺参数优化等研究工作。
中药材干燥过程建模不能仅局限于中药材的宏观干燥特性,还应该从微观角度深入揭示干燥过程的质热传递机理,并对干燥过程的有效成分变化进行模拟和定量分析。考虑到中药材干燥过程的复杂性,以后可以考虑采用智能模型与机理模型相结合的混合建模方法建立干燥过程的传热传质数学模型,以提升模型的准确性和可解释性。同时,还可以充分利用国内外新型的检测设备(属于直接检测法,例如:近红外光谱仪)或者软测量技术(属于间接检测法)以及新型干燥设备,以实现干燥过程重要数据(特别是中药材有效成分含量)的精准采集,并提高自动化和智能化水平,最终实现中药材加工生产过程的绿色、高效及高品质干燥[3]。
利益冲突所有作者均声明不存在利益冲突
