基于距离修正的小目标中波红外光谱辐射测温方法

李文凯, 周 亮, 刘朝晖, 崔 凯, 刘 凯, 李治国, 谢梅林

1. 中国科学院西安光学精密机械研究所, 陕西 西安 710119

2. 中国科学院大学, 北京 100049

引 言

随着红外辐射特性测量的深入研究以及红外技术应用的快速发展, 目前非合作目标的红外辐射特性信息受到了越来越广泛的关注。 在轨飞行的非合作目标的红外特性可直接反映出目标的物理特性, 获取非合作目标的红外特性信息可以反演目标的辐射亮度、 温度、 辐射照度等信息。 获取这些特征信息, 是空间目标深度识别的重要手段之一。 对高速运动的空间目标而言, 温度是表征其工作状态与性能的重要参数之一。 准确测量目标的温度对判别其运动状态、 预测其态势发展和完善空间目标态势感知获取手段具有重要的参考价值。

在实际工程应用中, 空间目标往往距离测量系统较远, 在探测器靶面上以少量像素呈现, 此时目标不能简单地当作面源目标或者点源目标进行处理, 必须作为小目标处理。 针对小目标红外辐射特性测量和温度特征提取这一领域, 国内外学者进行了大量研究。 1995年, de Jong[1]介绍了红外搜索与跟踪系统(infrared search and track system, IRST)的应用前景, IRST可以在远处警告来袭的小型目标, 如敌机和直升机等。 国内长春光机所的常松涛等[2]针对远距离小目标无法使用面目标和传统意义上点目标数据处理方法的问题, 提出了一种针对红外小目标的辐射特性测量方法, 适用于远距离小目标的辐射特性测量。 对于高温小目标而言, 田棋杰等[3]提出在测量过程中易受探测器饱和效应的影响, 为保证较高的测量精度, 使用辐射亮度定标模型时必须降低探测器积分时间, 当最低积分时间无法满足动态范围要求时, 则需要在光学系统中加入能量衰减装置, 对入射能量进行衰减。 因此, 在对高温目标进行高精度测量时, 其使用的定标模型存在着在单一积分时间下测温范围窄的缺点且辐射亮度测量误差最大在20%左右, 温度测量的最大相对误差在7%左右。

传统的利用辐射亮度来推测目标温度的方法测温精度较低, 而多光谱测温方法通过分析目标的光谱来获取目标的发射率和温度信息, 提升了测温精度, 在辐射测温领域应用十分广泛。 自Pyatt[4]在1954年提出多光谱测温法后, 经过数十年的发展, 我国在多光谱测温领域有了诸多研究成果。 哈尔滨工业大学的孙晓刚教授[5]将神经网络技术应用于多光谱辐射测温领域; 张福才[6-7]将优化的思想应用于多光谱辐射测温的数据处理; 2021年, 孙博君等[8]提出了一种多光谱真温快速反演方法。 但他们使用的多光谱测温装置为狭缝式光谱仪, 研究的目标多为短距离下的静态目标, 对远距离未知的动态小目标进行温度特征提取比较困难。

无狭缝光谱仪去掉了传统光谱仪的狭缝装置, 可大大降低对空间目标的跟踪和稳定精度的要求, 具有结构简单、 帧频高、 响应速度快等特点, 已经应用在天文观测[9]和航天器再入大气层观测[10]等领域。 本工作借鉴了基于传统辐射定标的模型, 结合了多光谱测温法测温精度高和无狭缝光谱仪的优势, 提出了一种减小成像距离影响的修正模型来对定标参数的上下界进行数值优化, 并进行了内外场试验验证, 结果表明可以有效地提高对目标的测温精度。

1 红外辐射光谱定标模型

目前常用的基于辐射亮度的红外辐射特性测量系统辐射定标模型[11]为

DN=αLt+B0

(1)

式(1)中,DN为红外探测系统的输出值,α为响应率,B0为偏置量,Lt为目标的辐射亮度。

为了更简便地分析目标的辐射特性, 以目标在一定窄波段内发射率近似相等为前提, 可将目标近似看作为灰体[12]。 红外光学系统采集目标的示意图如图1所示, 目标有效辐射面积为At, 温度为T, 发射率为εt。 目标发出的红外辐射被光学系统接收后会聚在探测器像面处, 通过信号处理模块将红外探测器采集到的辐射通量转换为灰度值。 红外探测器像元在线性区间内的辐射通量响应模型[13]为

(2)

图1 红外光学系统采集目标示意图

式(2)中,λ1、λ2为单像元对应的波长上下界,φt为目标到达光学系统像面处的辐射通量,DN0为由红外探测系统自身热辐射和背景辐射等因素引起的偏置值,a为响应率,τo为光学系统的透过率,R为目标与光学系统入瞳之间的距离,Ao为光学系统的入瞳面积,c1为第一辐射常数,c2为第二辐射常数。

在光学系统中引入光栅后, 需要考虑到光栅响应率对灰度值的影响, 还需要考虑到实际应用中大气衰减和红外探测器响应率的影响, 所以最终的红外辐射光谱定标模型为

(3)

式(3)中,τa为大气透过率,rID(λ)为红外探测器的响应率,rG(λ)为光栅的响应率。 光谱辐射定标即为获取某一窄波段范围内每一个波长λ对应的响应率a和偏置值DN0。 取该波段内a和DN0的最小值与最大值作为反演温度算法中所需输入a和DN0的上下界, 便可反演出目标的温度。

2 距离修正模型

根据式(1)常用的辐射定标模型, 往往使用在实验室中平行光管法标定的系数或者是在外场环境使用近距离扩展源法标定的系数。 尽管目标的温度与成像距离弱相关, 但随着成像距离R的增加, 其光谱识别特征表现得极为微弱, 若使用传统辐射特性测量的思路, 在不同成像距离处使用相同的定标参数, 将会增大对目标的测温误差。 而目标的红外辐射光谱表现的是灰度值随波长的分布, 其整体趋势基本不受成像距离的影响, 但是灰度值受成像距离R的影响较大, 由式(3)可知成像距离R的增大将会导致灰度值急剧减小。 为了减小成像距离R对测温精度的影响, 提出了一种对定标参数进行修正的模型, 建立了成像距离R与参数β的对应关系, 具体的函数表达式为

(4)

式(4)中,p1,p2为待测参数。 在对目标进行一维光谱处理时, 由于红外探测器和光栅的光谱响应为波长的函数, 优先消除红外探测器和光栅的光谱响应的影响, 则灰度值与波长的对应关系变为

(5)

根据式(5), 参数β、 响应率a与成像距离R三者之间的关系为

(6)

由式(3)可知, 当成像距离R取不同值时, 都会得到一组响应率a上下界的计算值, 再根据式(6)便可求得参数β上下界的计算值。 将成像距离R和参数β上下界的计算值代入式(4)便可得到参数β上下界对应的函数表达式βmax和βmin。 在拍摄目标时, 首先需要利用测距系统获取目标的距离信息, 将成像距离R代入βmax和βmin便可计算出该距离条件下参数β的上下界; 最后将成像距离R和参数β的上下界代入式(5)便可得到在该距离条件下响应率a上下界的计算值, 即完成对响应率a的数值修正。

3 实验部分

为了采集目标的红外光谱信息, 自主设计了基于无狭缝光栅光谱仪的试验样机, 实物图与实验光路示意图如图2所示。 利用黑体和平行光管模拟远距离小目标发出的红外辐射, 使其平行入射至光栅进行光谱分光, 再由中波红外热像仪采集目标的红外光谱图像, 由计算机对光谱数据进行存储。 所用黑体为便携式中温腔式黑体, 有效辐射直径为25 mm, 发射率为0.99; 平行光管焦距为3 m; 光栅为反射式衍射闪耀光栅, 尺寸为25.0 mm×50.0 mm×9.5 mm(W×H×D), 闪耀波长为3.5 μm, 刻线密度为300 Grooves·mm-1, 闪耀角为26.5°; 中波红外热像仪的工作波段为3.7～4.8 μm, 像元尺寸为15 μm×15 μm, 焦平面阵列像素为640×512, 镜头焦距为50 mm, F#为4。

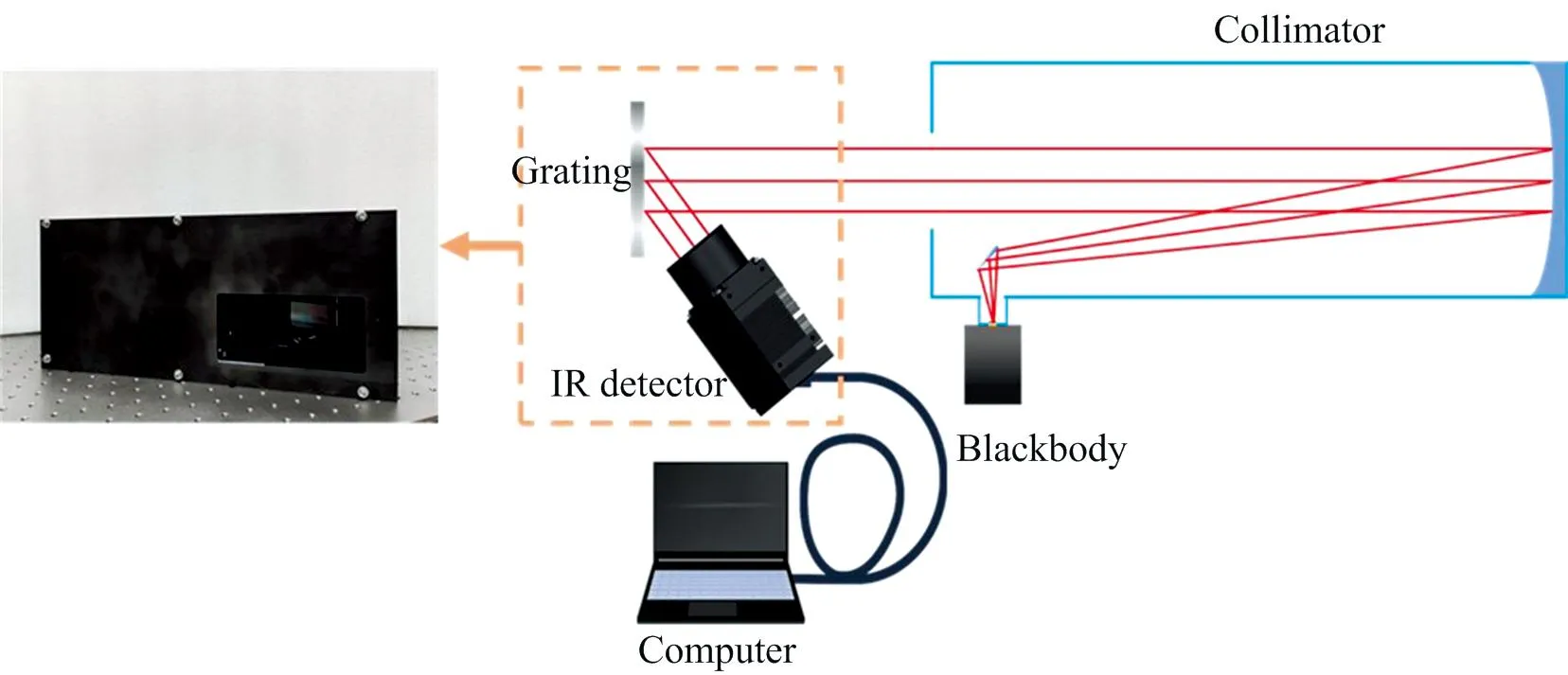
图2 基于无狭缝光栅光谱仪的实验光路图

利用试验样机开展光谱辐射定标实验, 设置红外热像仪的积分时间为1 ms, 采集不同温度条件下, 直径为10 mm的黑体靶标光谱图像, 光谱图像示意图如图3所示。 由于目标所处的环境不能保证完全相同, 且探测器易受自身的暗电流和热噪声的影响, 暗场噪声就不同, 因此在对样本进行分析时必须要减去暗场噪声的影响, 使得到的光谱更接近目标真实的光谱图像。 图4为经暗场噪声消除后的10 mm黑体靶标三维红外光谱。

图3 10 mm黑体靶标红外光谱图像

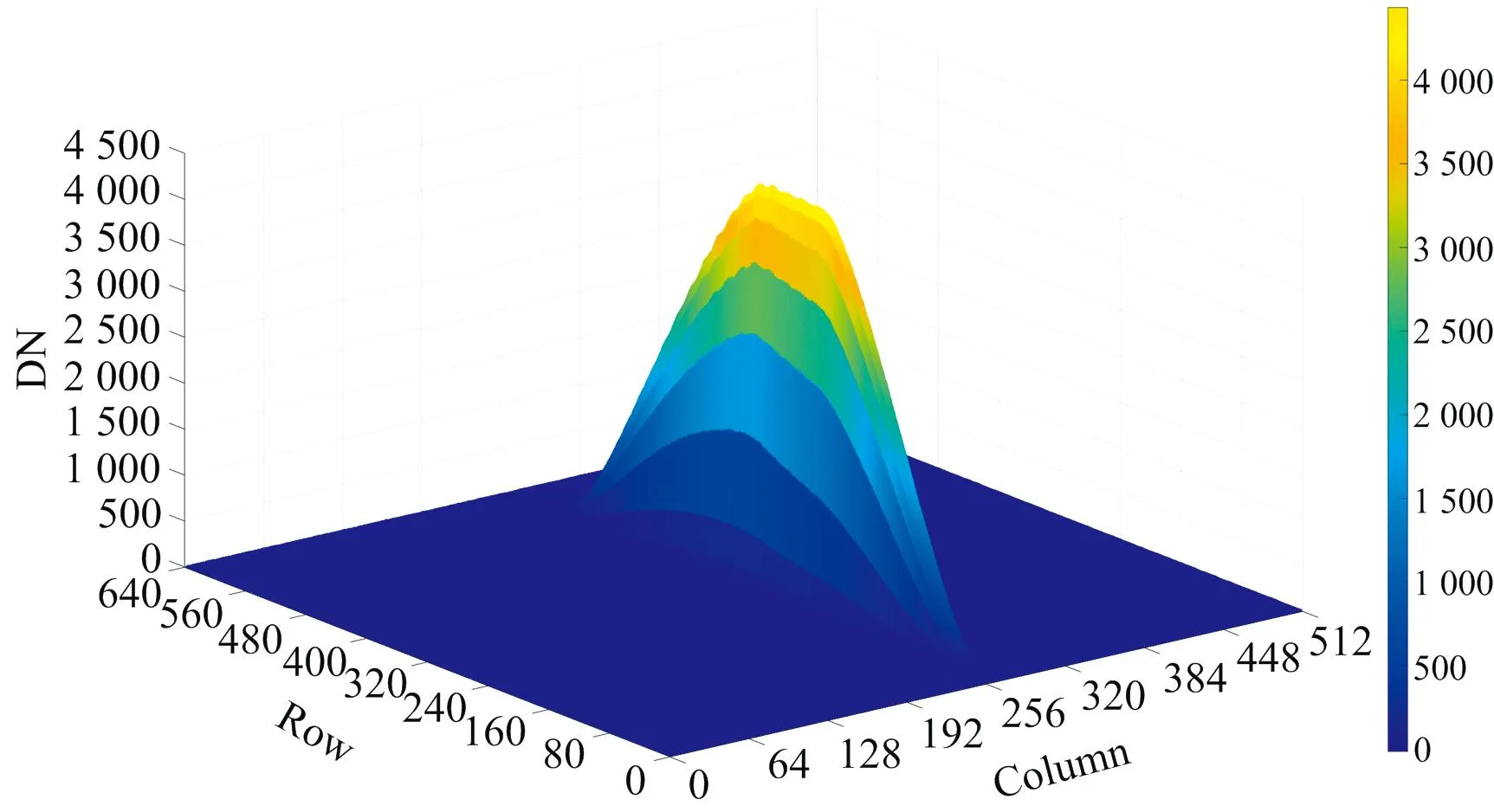
图4 消除暗场噪声的10 mm黑体靶标三维红外光谱图

将三维光谱数据进行抽谱处理, 得到目标的一维光谱曲线, 现在的一维光谱只是像素位置与灰度值的对应, 因此还需要进行波长校准, 求得像素位置与波长的表达式。 本文使用的波长校准的方法是根据中波红外滤光片的出峰位置建立像素位置与波长的对应关系, 黑体靶标通过滤光片后的出峰位置如图5所示。

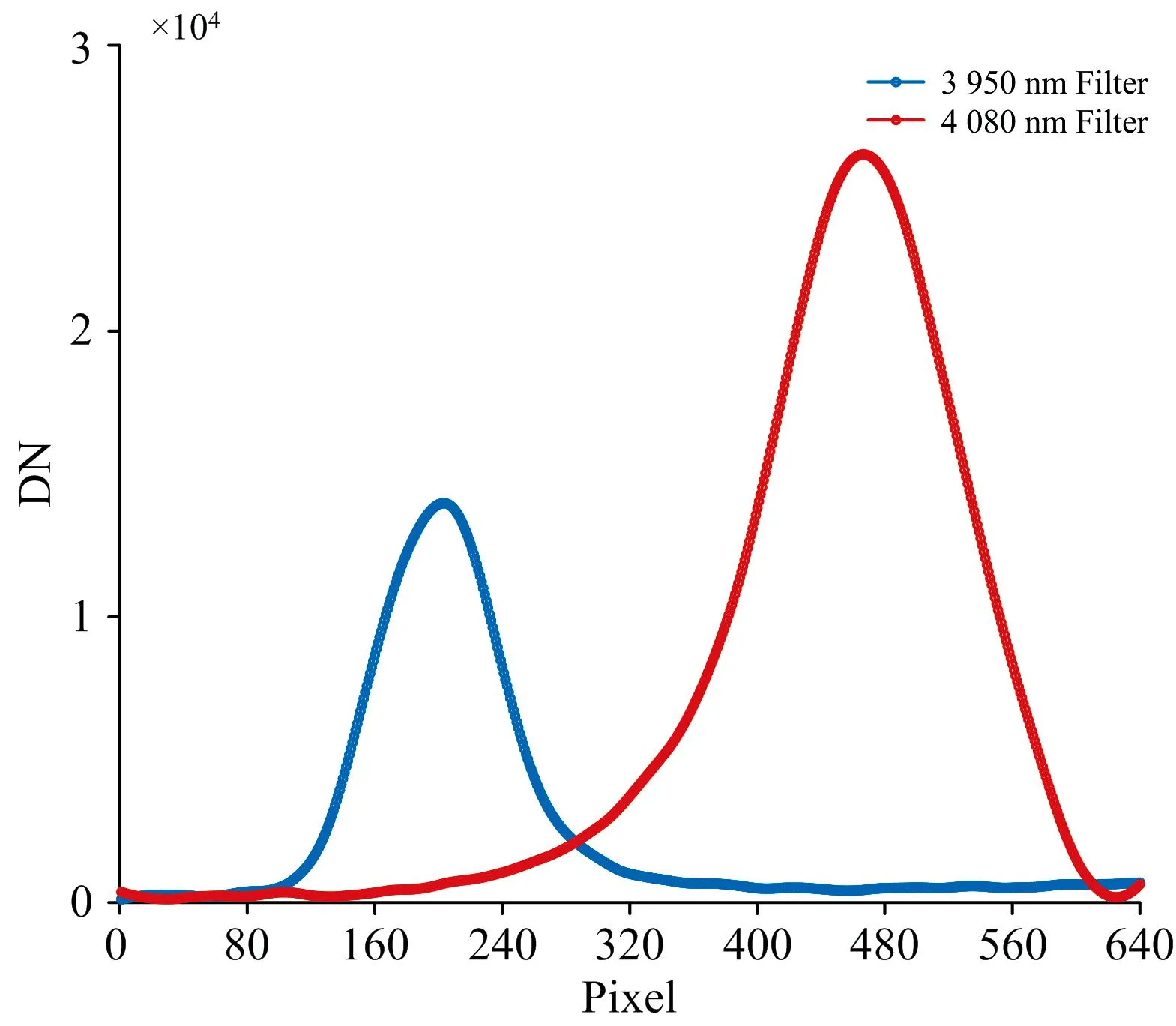
图5 滤光片与像素位置的对应关系

根据黑体靶标通过中心波长为3 950和4 080 nm滤光片的出峰位置, 确定的像素位置与波长的表达式为

λ(μm)=4.943 0×10-4pixel+3.849 7

(7)

根据式(6)便可以确定目标一维光谱的横坐标对应的波长数值。 目标在不同温度下的一维光谱如图6(a)所示, 黑体辐射特性曲线如图6(b)所示, 红外探测器和光栅的光谱响应曲线如图6(c)所示。

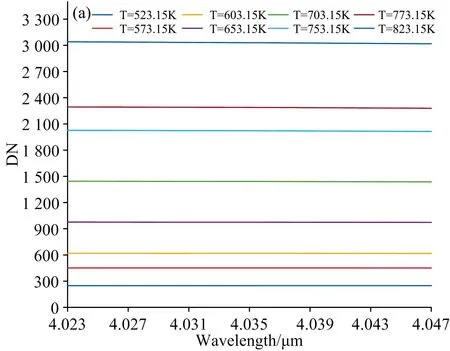
图6 (a) 目标在不同温度下的一维光谱; (b) 黑体在不同温度下的辐射特性曲线; (c) 红外探测器和光栅的光谱响应曲线

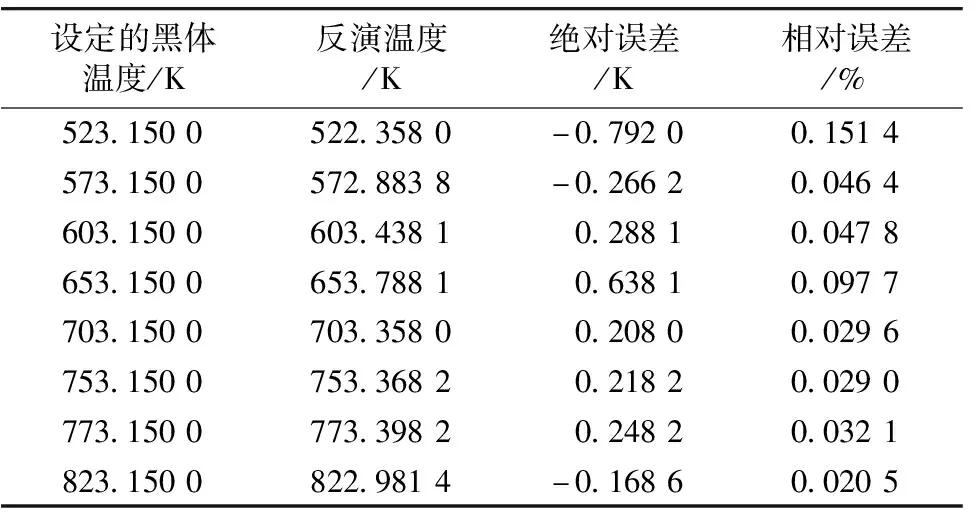
表1 计算的温度值

由表1可知, 在实验室环境对250～550 ℃温度范围的黑体靶标, 该算法反演的目标温度绝对误差在±0.8 K范围内, 平均相对误差为0.056 8%, 反演精度较高。

4 结果与讨论

在外场试验中, 针对10、 16、 28和60 m四个成像距离, 对25 mm的黑体靶标进行了光谱特性测量试验, 在图7中展示了目标在不同温度和不同距离条件下的灰度值。

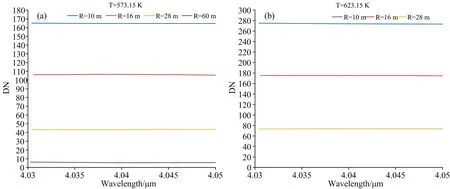
图7 不同温度下不同距离目标的灰度值

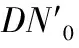
表2 使用实验室标定系数反演的温度结果

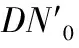
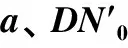
表3 不同距离下和β的计算值

由表3可知,βmin满足的表达式为

(8)

βmax满足的表达式为

(9)

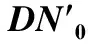
表4 修正a与后反演的温度结果

由表4所列结果可知, (1)10 m处的平均相对误差比16和28 m处的平均相对误差略大, 主要原因是10 m距离处的靶标尺寸在小目标所占像元数的临界值附近, 受抽谱方法的影响较大; (2)随着成像距离R的增加, 60 m处反演的温度最大相对误差为2.351 0%, 相比于使用实验室中标定的系数得到的24.736 8%的最大相对误差, 已有了很大的提升; (3)在四个成像距离内, 反演的目标温度整体平均相对误差为0.885 1%, 满足在实际应用过程中对小目标进行测温的精度需求。

5 结 论