基于高光谱数据的地表水化学需氧量反演

王雪映, 刘适搏, 朱继伟, 马婷婷

1. 中国科学院长春光学精密机械与物理研究所, 吉林 长春 130033

2. 中国科学院大学, 北京 100049

3. 长春长光格瑞光电技术有限公司, 吉林 长春 130102

4. 吉林省水文水资源局, 吉林 长春 130022

引 言

化学需氧量(chemical oxygen demand, COD)是水样在一定条件下, 氧化1 L水样中还原性物质所消耗氧化剂的量, 以mg·L-1表示, 它反映了水中受还原性物质的污染程度[1], 是水质评价的重要指标, 其数值越大, 代表水质越差, 受污染越严重[2]。 目前国际社会普遍公认的COD检测的经典标准方法为重铬酸盐法, 此外还有高锰酸钾法、 分光光度法、 快速消解法等检测方法。 这些方法虽检测精度较高, 但存在操作繁琐、 使用有毒试剂、 易造成二次污染等缺点。

高光谱技术是水质检测技术发展的新趋势, 具有检测快捷、 无需使用有毒试剂、 无二次污染等优点。 基于高光谱数据反演COD浓度早有研究, 林剑远等对嘉兴市主城区河网的COD等水质参数进行了反演, 基于航空和水表高光谱遥感数据, 对水质采样化验数据和水表反射率进行相关性分析, 计算出最佳波段组合并进行回归分析和拟合, 研究表明COD的最优拟合模型为二次多项式模型, 其决定系数R2和均方差RMSE分别为0.74和2.79[3]。 埃及的Elsayed等基于高光谱数据对卡龙湖中的多个水质参数进行了评估, 使用手持光谱仪采集水体光谱反射率, 利用已发布的光谱反射率指数、 新两波段光谱反射率指数和新三波段光谱反射率指数以及人工神经网络建立模型, 发现新三波段光谱指数与COD具有中等相关性,R2在0.52～0.64之间[4]。 董月群等以广东省鹤山市沙坪河为研究区域, 通过无人机高光谱成像遥感数据对城市河网的COD等水质参数进行反演研究, 通过分析水表反射率0阶导数、 一阶导数、 二阶导数与水质参数浓度的相关性选取相关性最高的波段组合, 并用统计回归的方法建立模型, 研究结果显示一阶导数对应的线性拟合模型具有较好的反演精度,R2介于0.85～0.96之间[5]。

上述对地表水COD浓度的反演, 多是采用无人机载高光谱成像仪于室外高空拍摄或在室外利用手持光谱仪获得光谱数据, 目前少有在室内环境下采集地表水高光谱数据并进行COD反演的研究。 为了填补这一研究领域的空白, 拓展高光谱水质分析技术的使用范围, 本研究以地表水样本理化分析的实测值结果为参考值, 在实验室内拍摄并提取出其高光谱数据, 以标准漫反射板为参照计算相应的光谱反射率, 通过Pearson相关性分析提取出原始光谱和导数光谱数据中与COD浓度相关性较高的特征谱数据, 利用粒子群算法优化的最小二乘支持向量机(particle swarm optimization-least squares support vector machines, PSO-LSSVM)算法, 基于原始光谱、 一阶导数全谱、 二阶导数全谱、 一阶导数特征谱、 二阶导数特征谱5种光谱数据建立不同的COD反演模型, 通过决定系数(coefficient of determination,R2)、 均方差(root mean square error, RMSE)和相对偏差(relative percent deviation, RPD)分析比较这几种模型的预测精度和可靠性, 为开发实验室环境下高光谱水质分析设备进行技术储备。

1 实验部分

1.1 样品

地表水样本来源于吉林省内的新立城水库、 太平池水库、 松花江等流域的23个站点, 水样COD浓度的实测值以相应的理化分析结果为参考。 剔除具有极端实测值的样本后, 数据集样本总量为129个, COD浓度范围为1～60 mg·L-1, 其中有56个样本浓度在10～20 mg·L-1范围内。 采用随机抽样的方法抽取32个样本做验证集, 剩余的97个样本点做训练集, 使得训练集和验证集的样本个数比约为3∶1, 具体划分情况如表1所示。

表1 地表水样本COD浓度统计分析

1.2 数据采集

检测装置如图1所示, 实验仪器主要有高精密电驱位移台及其控制箱、 高光谱成像光谱仪、 计算机等; 实验材料及用品主要有地表水样品、 标准漫反射板等。 高光谱成像光谱仪采用的是长春长光格瑞光电技术有限公司自主研发的GRS-400PG推扫型成像光谱仪, 分辨率约2.4 nm, 光谱范围为400～1 000 nm; 实验光源选用四个25 W钨丝灯泡置于成像光谱仪前端镜头四周, 以更好地模拟室外太阳光的均匀性; 盛样皿口径为12 cm, 容积为400 mL; 选用的标准漫反射板的反射率为50%, 尺寸为13 cm×13 cm。

图1 检测装置实物图

数据采集时, 每个水样的取样量为250 mL, 将高光谱成像光谱仪固定于位移台垂直上方约50 cm处, 盖上遮光布, 驱动位移台匀速移动, 同步拍摄每个水样及标准漫反射板的高光谱图像, 重复采集10次以减少测试误差。

1.3 数据预处理

1.3.1 反射率计算

根据实验室内拍摄的高光谱数据计算水体光谱反射率公式为

(1)

式(1)中,R(λ)为不同波长的水体光谱反射率, 下标λ表示波长。DN水为探测器输出的代表水体辐射光谱强度的DN值数据,DNboard(λ)为同步获得的50%标准漫反射板的DN值数据,Rboard(λ)为50%标准漫反射板的反射率[6]。

1.3.2 导数法处理

为了降低背景噪声干扰, 提升光谱数据对COD浓度的敏感度, 采用导数法进行处理。 参考文献[7-8]处理导数光谱的方法, 计算导数光谱的公式为

(2)

(3)

式(2)和式(3)中,R,R1st,R2nd分别为原始光谱反射率值、 一阶导数光谱反射率值、 二阶导数光谱反射率值;λ为波长。

1.3.3 特征谱提取

高光谱数据具有波段多、 数据量大的特点, 提取特征谱段可以提高计算速度, 减少冗余噪声影响。 相关性分析是判断两个或多个变量之间统计学关联的方法, 相关系数是用以反映变量之间相关关系密切程度的统计指标。 采用Pearson相关性分析方法, 对特征谱段进行分析并提取, 其相关系数计算公式为

(4)

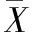
Pearson相关系数的范围为[-1, 1], 其值越接近于1或-1, 表明相关性越强; 相关系数越接近于0, 表明相关性越弱。

1.4 反演模型

最小二乘支持向量机(least squares support vector machines, LSSVM)是在支持向量机(support vector machine, SVM)中引入最小二乘线性系统作损失函数的机器学习方法, 用二次损失函数取代SVM中的不敏感损失函数, 通过构造损失函数将SVM的二次寻优变为求解线性方程。 该方法简化了运算复杂性, 提升了运算速度, 通过结构风险最小化原理可提高模型泛化能力, 可以有效解决传统学习方法处理有限样本数据、 非线性、 高维数等问题的困难, 越来越广泛地被应用于非线性复杂系统的建模中。 径向基核函数(radial basis function, RBF)应用广泛、 适用性强、 具有较宽收敛域, 对非线性系统具有很好的控制性能, 几乎任何情况(维数过高过低、 样本数据过多过少等)下, 均能表现出较理想的效果[9], 因此本研究选用RBF核函数作为模型的核函数。

在LSSVM模型中, 正则化参数和核函数参数的选择对构造回归函数是至关重要的, 直接影响着模型的学习和泛化能力。 优化模型参数的常用方法有遗传算法(genetic algorithm, GA)[10]、 粒子群算法(particle swarm optimization, PSO)[11-13]、 蝙蝠算法(bat algorithm, BA)[14]和灰狼算法(grey wolf optimizer, GWO)[15]等。 本研究选用了PSO算法来优化寻参, 它是一种模拟鸟群觅食的群体智能算法, 将只有位置和速度两个属性的粒子模拟为鸟, 每个粒子在空间中的极值作为潜在的最优解; 所有粒子根据评价函数决定的适应值不断调整各自的位置和速度, 以寻找最优解。

设置粒子种群数量为20, 最高迭代次数为50, 正则化参数γ和核函数参数σ的取值范围均设置为[0.01, 100], 采用K折交叉验证对数据集进行训练调整,K取值为5, 用交叉验证的均方差RMSE作为评价函数的适应值。 经过PSO算法计算, 可得到正则化参数γ和核函数参数σ的最优参数值, 将其代入LSSVM算法中, 可以使LSSVM算法有较强的适应能力和较好的预测精度。

1.5 模型评价

采用决定系数R2、 均方差RMSE和相对偏差RPD三个指标用于模型对比和评价

(5)

(6)

(7)

2 结果与讨论

2.1 水体反射率

图2(a)为样本水体的原始光谱曲线, 水体在波长400～620 nm处反射率较高, 在波长750～900 nm处反射率迅速下降。 使用导数法对原始光谱进行一阶导数、 二阶导数处理, 所得的地表水光谱反射率数据分布如图2(b)、 (c)所示。 对比分析可得: 导数处理有效强化了光谱曲线的特征, 呈现出较多的波峰、 波谷; 但仍无法直观判断出各波段水体光谱反射率与地表水样COD浓度间的明显线性关系。

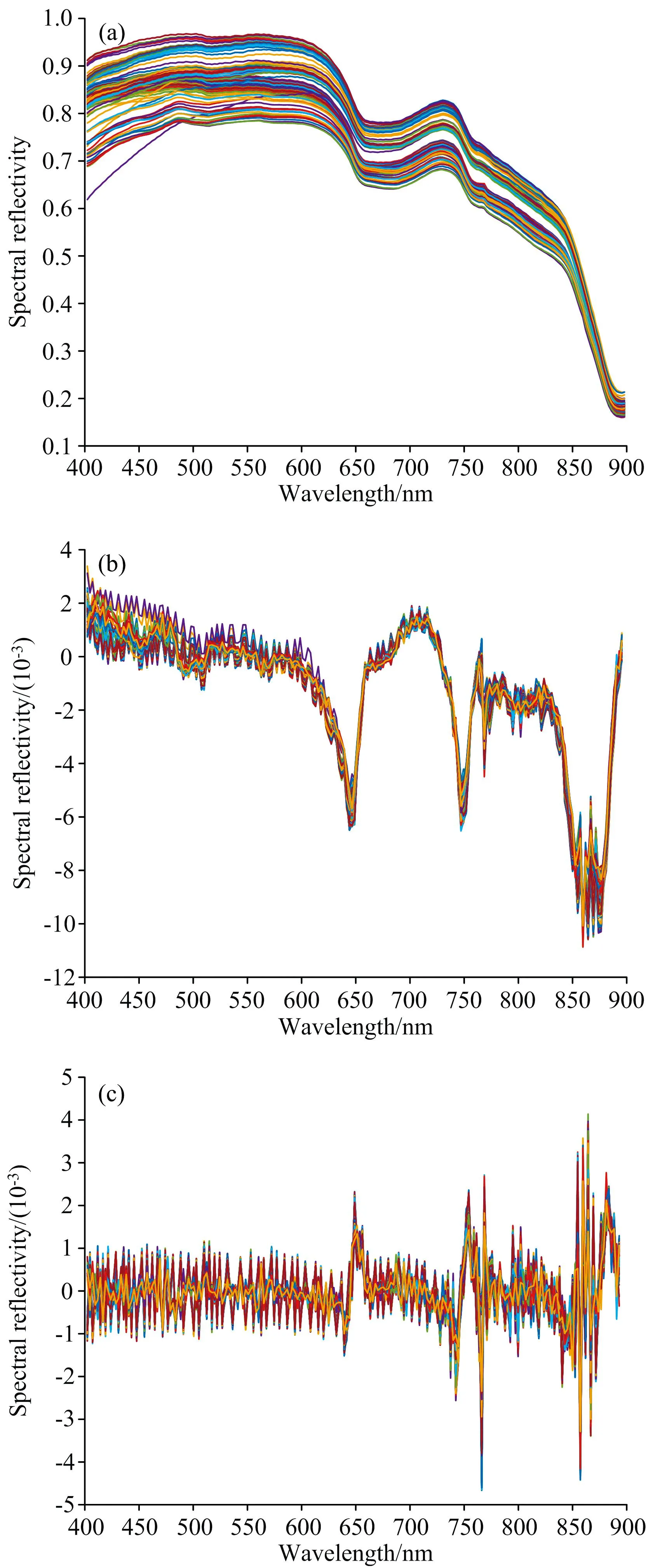
图2 水体光谱反射率

2.2 相关性分析与特征谱提取

以训练集样本数据为相关性分析对象, 对水样的光谱反射率数据和COD浓度实测值进行相关性分析, 所得Pearson相关系数如图3所示。 未经处理的原始光谱反射率数据的相关性较小, 整体变化趋势为相关性随波长的增大而增大, 在波长872 nm处相关性最大, 相关系数为-0.309 8。 一阶导数、 二阶导数光谱反射率数据存在相关性较大的波段, 无相关系数随波长变化的趋势。 其中, 一阶导数光谱在波长436 nm处相关性最大, 相关系数为-0.496 8; 二阶导数光谱的相关系数波动很大, 和一阶导光谱相比有更多明显的峰值, 在波长855 nm处相关性最大, 相关系数为0.483 5。 以上结果说明, 原始光谱对COD浓度变化的敏感度较低, 在本研究中导数光谱与地表水的COD浓度之间的相关性相对更高, 利用导数光谱数据建模可能具有更高的预测精度。

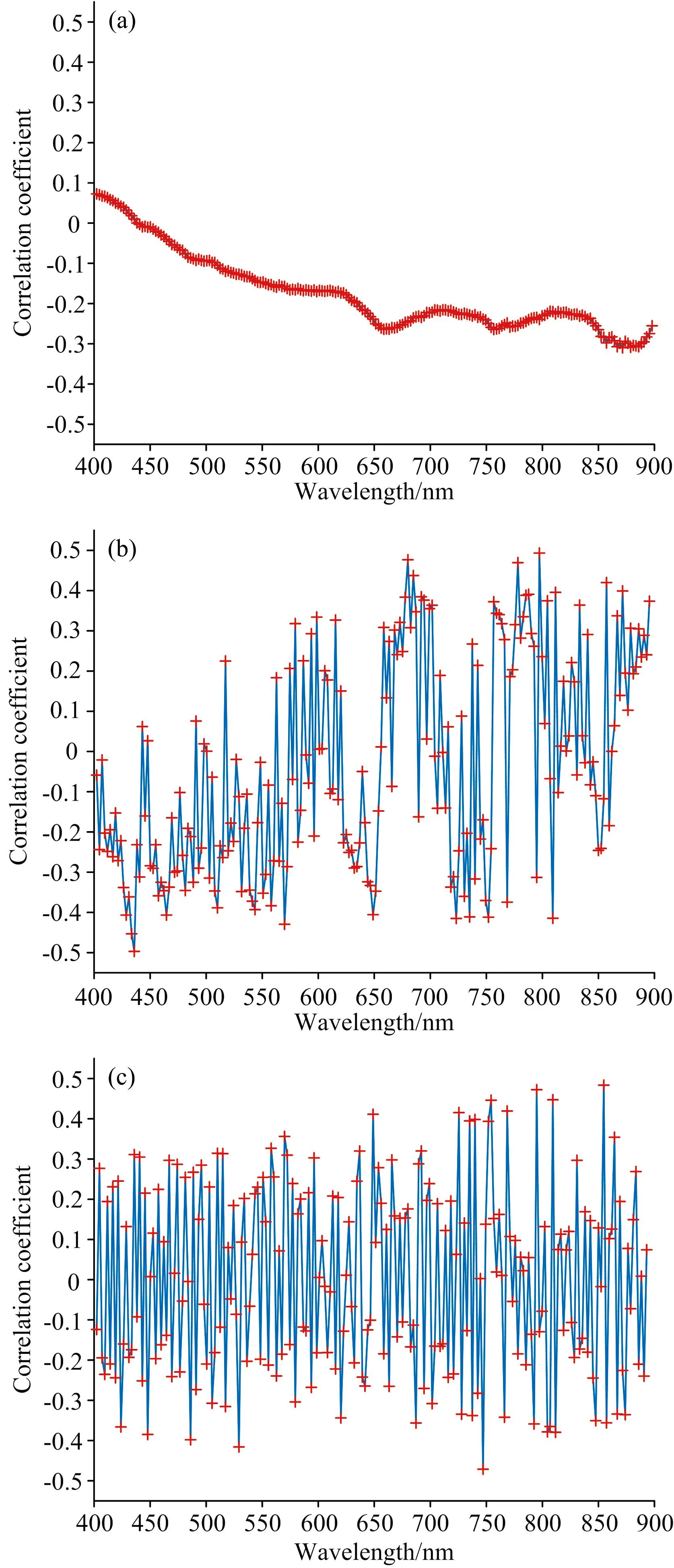
图3 训练集相关系数

基于上述相关性分析结果, 分别选出相关系数绝对值大于0.35的波段作为特征谱段, 对应的特征谱相关系数分布情况如图4所示。 一阶导数光谱相关性较好的波长共有38个, 主要分布在在648～811 nm处; 二阶导光谱相关性较好的波长共有24个, 主要分布在在725～811 nm处。

图4 特征谱相关系数

2.3 建模反演结果及对比

根据Pearson相关性分析结果提取特征谱数据, 利用PSO-LSSVM算法基于训练集数据建立COD浓度反演模型, 然后将验证集数据代入所建模型中加以验证以确定最优反演模型。 由于PSO-LSSVM模型的运行结果具有不确定性, 因此每组模型运行10次后取平均值来作为最终结果。

在采用全谱数据建模时, 对训练集原始光谱数据、 一阶导数光谱数据、 二阶导数光谱数据三类数据, 取其波长400～900 nm内全谱数据数据, 利用PSO-LSSVM算法进行建模, 训练集和验证集的预测结果分别如图5和图6所示。

图5 利用全谱数据建模的训练集预测结果

图6 利用全谱数据建模的验证集预测结果

在采用特征谱数据建模时, 因在对原始光谱数据进行相关性分析时未能找到特征波长, 故只对训练集一阶导数特征光谱数据、 二阶导数特征光谱数据进行建模与分析。 根据相关性分析结果, 以相关系数绝对值大于0.35为筛选准则确定特征光谱, 利用PSO-LSSVM算法进行建模, 训练集和验证集的预测结果分别如图7和图8所示。

图7 利用特征谱数据建模的训练集预测结果

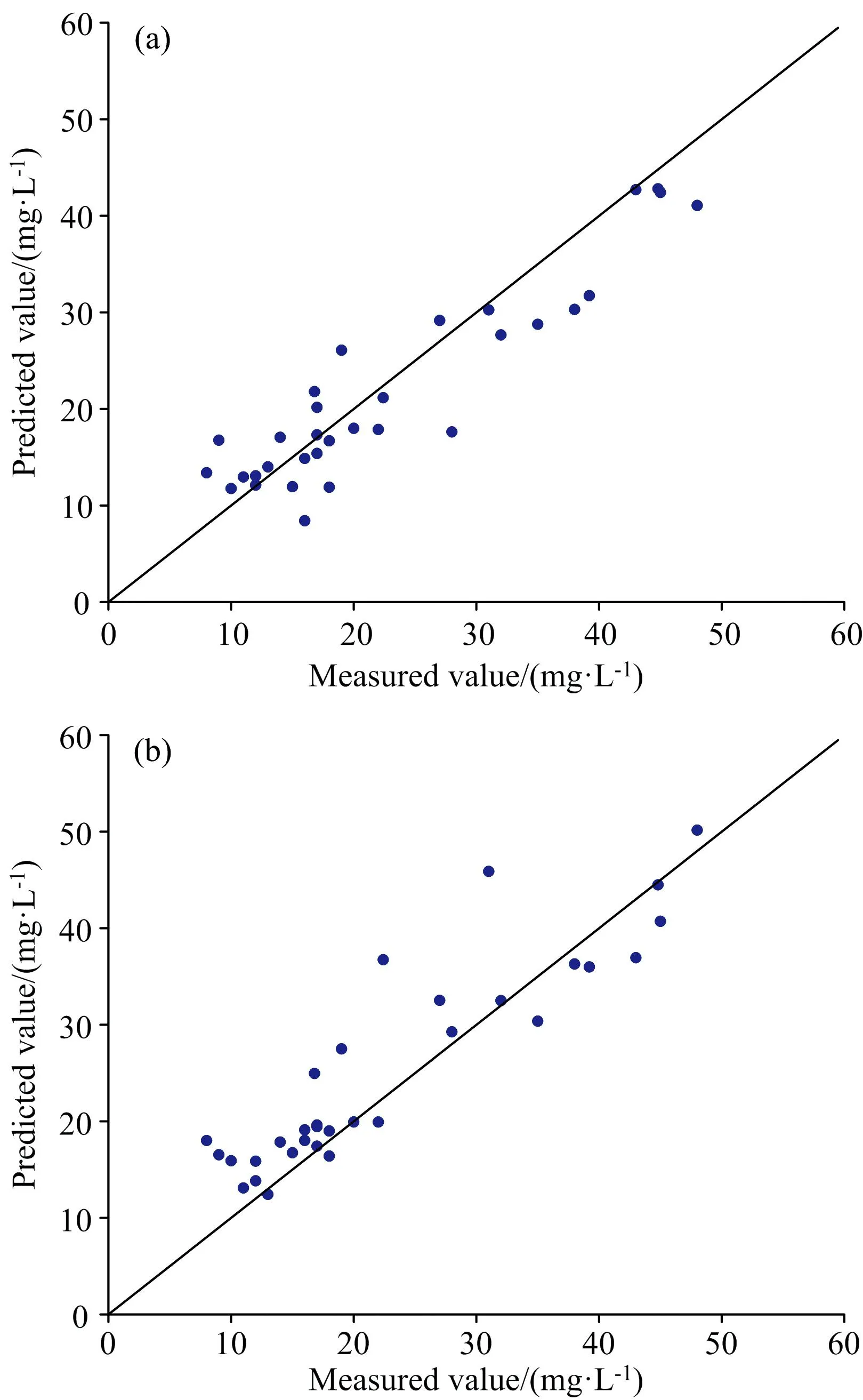
图8 利用特征谱数据建模的验证集预测结果

表2给出了利用全谱数据和特征谱数据建模时训练集和验证集预测结果的R2、 RMSE和RPD。 训练集的交叉验证结果中, 利用一阶全谱、 一阶特征谱、 二阶特征谱数据建模的R2均大于0.98, RMSE均小于1.5, RPD均大于9, 远远优于利用原始谱和二阶全谱数据建模的结果, 说明前三种模型具有较强的适应能力和较好的预测精度。 验证集的预测结果中, 利用原始光谱建模的R2和RPD较低, RMSE较高, 表明其预测效果较差; 利用导数光谱数据建模的R2和RPD较高, RMSE较低, 表明其具有较好的预测效果; 其中利用一阶导数特征谱建模时预测结果最好,R2和RPD最大, RMSE最小。 同时, 训练集的交叉验证结果和验证集的预测结果都出现了经同阶导数预处理后利用特征谱数据建模结果优于利用全谱数据建模结果的情况。

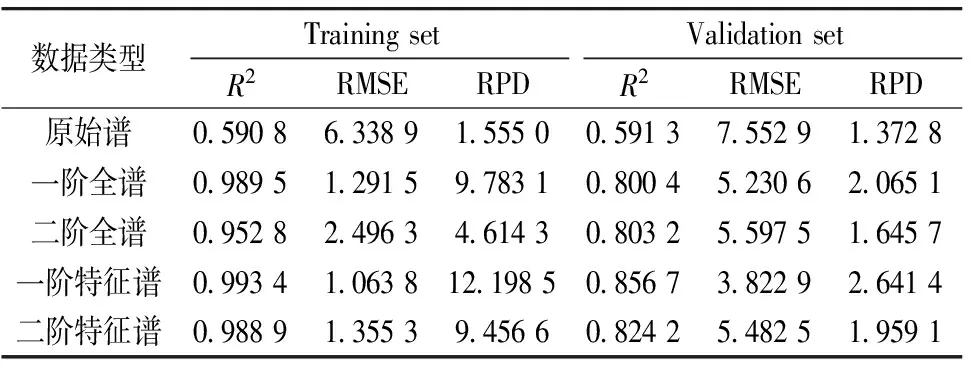
表2 地表水COD浓度的预测结果评价

实验结果表明, 利用原始光谱数据建模的模型预测能力较差, 而利用导数光谱数据进行建模可以提高模型的预测精度; 另外, 对于导数光谱数据, 提取特征谱数据所建立的模型比利用全谱数据建立的模型有更好地预测效果。

3 结 论

以吉林省的地表水样品为研究对象, 分析样品的高光谱数据和COD浓度实测值之间的相关性, 利用PSO-LSSVM算法建立地表水COD浓度的反演模型, 通过对相关反演方法的研究及对预测结果的分析, 得出如下结论:

(1)地表水COD浓度与原始光谱反射率的相关性较弱, 无明显特征波长。 经过导数法预处理后, 地表水COD浓度与光谱反射率的相关性明显增强。

(2)利用特征谱数据建模的结果要优于利用全谱数据建模的结果, 其中利用一阶导数特征谱建模反演地表水COD浓度的效果最好, 精度最高, 训练集的R2、 RMSE和RPD分别为0.993 4、 1.063 8和12.198 5, 验证集的R2、 RMSE和RPD分别为0.856 7、 3.822 9和2.641 4。

(3)在室内基于高光谱数据反演地表水COD浓度的应用具有可行性, 验证了所提出的基于PSO-LSSVM算法、 导数处理法、 Pearson相关性分析法建立的地表水COD浓度反演模型, 能达到较好反演精度。 并且, 未来随地表水样本数据量的不断积累, 在反演模型的适用浓度、 反演精度、 模型的稳健性等方面都将得到提升, 日后也将进一步探究基于高光谱数据和PSO-LSSVM算法估测其他水质参数的可能性。