基于权重的AHP判断矩阵一致性调整方法

耿正霖,吴佳妮,程兴华,包长春

(国防科技大学 气象海洋学院, 湖南 长沙 410073)

层次分析法[1](analytic hierarchy process,AHP)是一种综合定性与定量分析的多指标、多准则的综合评价方法,为定量分析定性事件提供了一种有效的技术手段,在经济、社会、管理、军事等诸多领域得到了广泛应用[2-8]。其基本原理是由决策者(decision maker, DM)对不同指标进行两两比较,构建一个判断矩阵(pairwise comparison matrix, PCM),通过判断矩阵进行分析得出不同指标的权重[1]。判断矩阵描述了决策者对不同比较因素的判决,但该判断通常有主观性,可能出现前后不一致的情况,即构造出来的判断矩阵可能不满足一致性要求[9-10],导致计算出的权重难以保证决策的可靠性。因此,计算权重前通常需对判断矩阵进行一致性检测和元素值调整与修正,减小主观不一致对决策造成的影响。

目前,对判断矩阵进行修正,通常考虑两点:①使得改进后的判断矩阵满足一致性要求;②尽量保证对原始判断矩阵的修改不违背决策者的初衷。也就是在保证判断矩阵满足一致性要求的前提下,调整判断矩阵的元素值,使得调整后的判断矩阵与原始判断矩阵的差异程度最小[11]。这里所说的判断矩阵满足一致性要求,通常是指判断矩阵的一致性系数(consistency ratio,CR)小于0.1[1],该评判标准已广泛用于AHP一致性评价中。而矩阵调整程度可采用不同的指标进行衡量[11],例如判断矩阵各元素总的变化量[12]、判断矩阵各元素调整最大值[11,13]、判断矩阵调整元素个数[14]、判断矩阵元素调整比例[15-16]等。这些方法均以CR满足一致性要求为目标,通过不同评价指标对应算法进行判断矩阵的调整,直至判断矩阵满足一致性要求。

但是,目前对判断矩阵信息保留程度的评价标准都是从判断矩阵出发,以判断矩阵调整前后的变化量衡量对原判断信息的保留程度,却没有考虑调整后判断矩阵残留的不一致性(CR≠0)对最终权重计算结果的影响。因为当CR≠0时,矩阵的逻辑不一致性[17]可能并未完全消除,会导致计算权重时判断矩阵还存在逻辑矛盾,而且矩阵的数值不一致性也会对权重计算产生影响。两者都会使得权重所表述的各因素之间关系与原始判断产生偏离,也就是说,目前的方法并不能完全衡量最终判断结果(权重)对原始判断矩阵的保留程度。

因此,本文从判断结果出发,提出一种基于计算权重的AHP一致性调整方法,以最终计算权重对应的完全一致矩阵与原始判断矩阵差异最小为优化目标,进行判断矩阵调整,使权重能最大程度保留原始判断信息。

1 问题描述

通常,层次分析法的应用过程如图1所示。

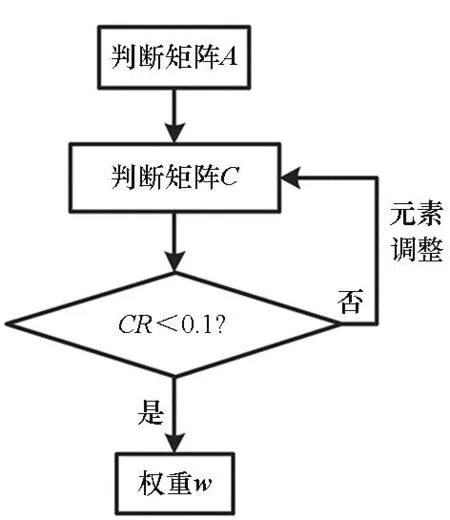
图1 层次分析法应用过程Fig.1 Process of AHP application

首先,决策者给出原始判断矩阵A,将A作为矩阵调整的初始值赋值给C,若C满足一致性要求(CR<0.1),则直接用C计算权重w;若C不满足一致性要求,则通过相应的准则进行矩阵调整,直至C满足一致性要求(CR<0.1),再根据矩阵C计算对应的权重w,以进行不同因素的重要性加权。

目前,大多文献关注的是矩阵调整前后的变化量X(X=C-A),以矩阵调整量的相应数据作为信息保留程度的衡量标准。但从层次分析法的应用看,最终目的是计算权重w,要使结果尽量保留决策者的判断,应该使最终计算得到的权重w所表示的元素之间的重要性关系能尽可能保留原始判断矩阵的信息,而不是调整后的矩阵C尽可能保留原始判断矩阵的信息。

权重w可以视为是根据判断矩阵所有元素得出的综合判决的结果,包含了各因素之间的重要性判断,其对应一个完全一致的矩阵B(B满足条件:对于任意的i,j,k,有bi,j=bi,kbk,j[18]),可以描述各因素两两之间的相对重要性。用完全一致矩阵B与原始判断矩阵A的差异来衡量判断矩阵元素调整对原始决策信息的保留程度更为合理。层次分析法过程中涉及的变量关系如图2所示。

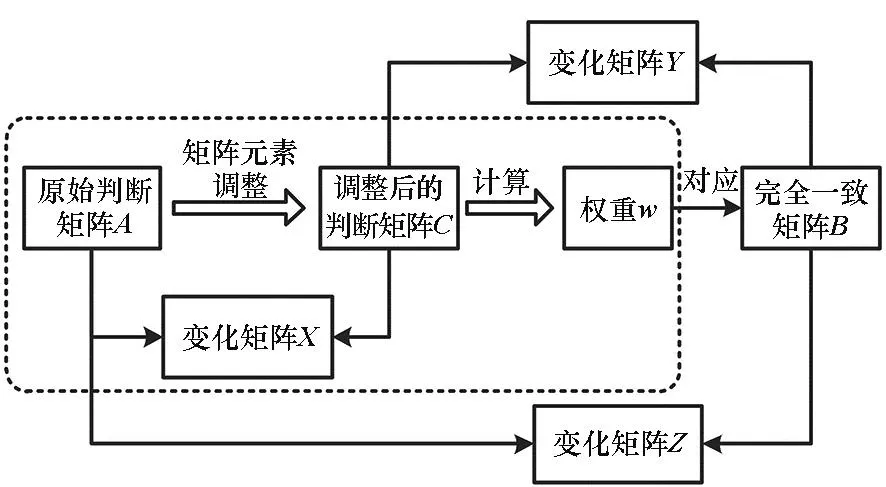
图2 矩阵相互关系示意图Fig.2 Schematic diagram of matrix interrelationships

在实际情况下,矩阵元素调整通常不能完全消除不一致性(CR≠0),此时,计算得到的权重所对应的完全一致矩阵B与用于计算权重的判断矩阵C存在差异,用矩阵Y表示(Y=B-C),该矩阵等效于将判断矩阵C进行调整得到一个完全一致矩阵B所进行的调整量。那么,权重所对应的完全一致矩阵B与原始判断矩阵存在的差异为矩阵X和Y的叠加,用矩阵Z表示,即Z=B-A。

可以看出,矩阵X是调整后的判断矩阵C相对于原始判断矩阵的改变量,而矩阵Z才是最终判断结果相对于原始判断矩阵的改变量。所以,通过矩阵Z更能衡量出判断结果即权重w对原始判断矩阵的改变程度或保留程度。因此,本文以矩阵Z各元素的平方和作为矩阵改变量的衡量标准,以其最小值为优化目标进行矩阵B的求解。

(1)

式中,N为元素个数。

此时,权重求解过程转化为求解一个完全一致矩阵,使其与原始判断矩阵差异最小的过程。这个完全一致矩阵与权重一一对应,求出矩阵就对应得到权重。权重w和完全一致矩阵B对应关系如下:

1)设w=[w1,w2,…,wN]T,则B可以由式(2)计算得到。

(2)

2)若已知完全一致矩阵B,则对其任意列进行归一化即可得到权重w。

(3)

从上述分析可知,本文目标就是通过矩阵元素调整,构造一个完全一致矩阵,使其相对于原始矩阵的改变量最小。

2 算法步骤

假设原始判断矩阵为A,表示为:

(4)

本文目的是求得一个完全一致矩阵B,使得A与B的差异最小,而B的任意列进行归一化后作为该判断矩阵计算得到的权重。这一过程也可以理解为一个带约束条件的优化问题:在保证最终结果为完全一致矩阵的条件下,使求得的矩阵与原始判断矩阵的差异程度最小。

显然,对于一个完全一致矩阵B,其秩为1,行列间相关,仅有N-1个独立的变量,只要确定N-1个独立的变量的值就能确定整个矩阵。不失一般性,可假设N-1个独立的变量为bm,m+1,其中1≤m≤N-1,则矩阵其他元素都可由这N-1个元素计算得到。矩阵B可依据式(5)构造:

(5)

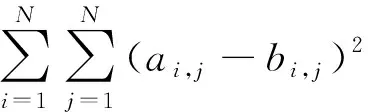
(6)

因为ai,i=bi,i=1,式(6)等效于:

(7)

要得到使得式(7)最小的bm,m+1(1≤m≤N-1),最简单的方式是通过在一定范围内遍历bm,m+1的取值,但该方法计算量较大,特别是当N较大时,若每个维度遍历数为M,总的遍历数量为MN-1。基于此原因,利用梯度最速下降法进行最优值的求解,主要步骤如下。

2.1 优化目标

2.2 梯度计算

计算p=f(b)的梯度,上式可以写为:

(8)

其中,bi,j对bn,n+1(1≤n≤N-1)求导得:

(9)

那么,计算得到1/bi,j对bn,n+1(1≤n≤N-1)求导的结果:

(10)

则可计算出p对bn,n+1(1≤n≤N-1)的导数:

(11)

那么,可根据式(11),求得p的梯度:

(12)

2.3 数据更新

传统梯度下降法对每一个参数的学习率是相同的,但实际中,不同参数的重要性不同,因此本文采用自适应梯度算法[19](adaptive gradient algorithm,AdaGrad)进行数据更新,对不同参数采用不同的学习率,使目标函数能更快收敛。

设梯度累计量为r,k表示迭代次数,k≥1,初始化r(0)=0,累计量的更新公式如下:

r(k)=r(k-1)+H(∇(k),∇(k))

(13)

式中,H(∇(k),∇(k))表示∇(k)和自身的Hadamard乘积。梯度的更新公式如下:

(14)

式中:γ为学习率;δ为一个极小量,避免分母为0。因为原始判断矩阵元素在[1/9,9]内分布,b初值各个元素也在[1/9,9]内分布,为避免调整量过大,可控制γ大小使得最大调整量在一定的范围内。

可以看出,AdaGrad算法第一次调整值约为学习率,如果学习率超过了初值或者很接近初值,会导致调整后的元素接近于0,其对应的倒数值会很大,使得结果不收敛或者收敛到错误结果。故初值和学习率的选择原则为:

1)采用原始判断矩阵的次对角阵元素为初值;在无其他信息时,原始判断矩阵具有较高的参考价值。

2)学习率的选择,可根据初值元素中的最小值设定,为避免调整后特别是首次调整后矩阵元素接近0,设置学习率为最小元素值的1/2。

2.4 迭代计算

计算b(k)对应的p(k),当|p(k)-p(k-1)|<ε停止迭代,其中ε为一个很小的正数。假设此时迭代次数为K,以此时的b(K)作为b的最终解。

2.5 权重计算

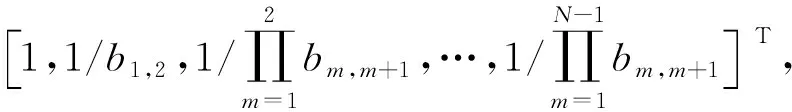
(15)

通过上述方法,可以根据梯度大小自动调整变化量的大小和方向,加快矩阵调整速率,使得b较快收敛到最小值点,得到改变量较小的矩阵B,同时得到对应的权重w。

3 算例分析

利用MATLAB对上述算法进行验证分析,并与其他几种参考算法进行比较。计算经典算例下本文所述的完全一致矩阵改变量大小,以此衡量算法的性能。传统算法通常只计算得到一个满足一致性条件的判断矩阵,进而计算权重;本文利用权重计算其对应的完全一致矩阵,将其与原始判断矩阵进行比较。进行比较的算法如表1所示。

表1 主要比较算法

3.1 算例1

文献[20]、文献[11]和文献[13]均通过算例1进行算法性能的比较,其初始判断矩阵为:

3.1.1 文献[20]方法

文献[20]所述方法得到的调整后的判断矩阵为:

计算得到权重及对应的完全一致矩阵为:

将其与原始判断矩阵进行比较,总的改变量为54.981 7,最大改变量为6.996 7(a2,3)。

3.1.2 文献[11]方法

采用文献[11]所述方法得到的调整后的判断矩阵为:

计算得到权重及对应的完全一致矩阵为:

将其与原始判断矩阵进行比较,总的改变量为32.061 5,最大改变量为4.052 7(a2,3)。

3.1.3 文献[13]方法

采用文献[13]得到调整后的判断矩阵为:

计算得到权重及对应的完全一致矩阵为:

将其与原始判断矩阵进行比较,总的改变量为31.003 3,最大改变量为4.312 7(a2,3)。

3.1.4 本文方法

设小常数δ为10-7,循环停止条件ε为10-5,本文方法不同条件计算得到的结果如表2所示。

表2 算例1本文方法计算结果

从表2中结果看,不同的初值对最终的结果影响较小;随着学习率的下降,迭代次数增加。其总的矩阵改变量相比其他方法显著减小,最大改变量为a1,4。这里以表中条件1(起始值为原始判断矩阵次对角元素,γ=0.25)和条件4(起始值为全1矩阵,γ=0.25)的结果进行分析,其余条件下计算结果与之相似。

第1种条件下,对应完全一致矩阵为:

计算得到权重为:

参数收敛情况如图3所示。

图3 条件1参数收敛情况Fig.3 Convergence of parameters in case 1

第4种条件下,对应完全一致矩阵为:

计算得到权重为:

参数收敛情况如图4所示。

图4 条件4参数收敛情况Fig.4 Convergence of parameters in case 4

取不同起始值时权重差值为:

可以看出,不同的起始值条件下,随着迭代计算,b逐渐收敛到最终结果,两种情况下最终得到的权重差异很小。但采用全1列向量作为初始值时,其与收敛结果的差距较大,迭代次数较多。

3.2 算例2

以参考文献[13]和文献[17]采用的算例进行算法的比较。原始判断矩阵为A2。下面对几种典型方法的计算结果进行比较。

3.2.1 基本回路法[17]

根据文献[17],采用基本回路法对判断矩阵进行修改,得到修改后的矩阵为C5,该矩阵的CR=0.082 2,满足一致性要求,矩阵总的改变量为34.642 9,最大改变量为5.537 4(a3,7);利用此矩阵,计算得到权重,再得到对应的完全一致矩阵B5,将其与原始判断矩阵进行比较,总的改变量为224.428 1,最大改变量为9.854 7(a8,4)。

3.2.2 边界优化法[13]

采用边界优化法进行修改后的矩阵为C6,此时,矩阵的CR=0.099 8,满足一致性要求,总的改变量为13.103 8,最大改变量为0.718 6(a8,2);虽然矩阵的改变量很小,但此时的CR是相对较大的,说明此矩阵存在较大的不一致性,即判断存在一定的矛盾,以此得出的权重可靠性不高。此外还可以看出,调整后a3,7逻辑不一致并未改善。以此矩阵计算权重,得到其对应的等效完全一致矩阵B6,相对于原始判断矩阵,总的改变量为242.358 5,最大改变量为10.228 7(a8,4)。

3.2.3 本文方法

本文计算了不同参数条件下本文方法的计算结果,得到对应的迭代次数、矩阵改变量以及完全一致矩阵。其中设小常数δ为10-7,循环停止条件ε为10-5。结果如表3所示。

表3 算例2本文方法计算结果

不同条件下计算结果近似,仅迭代次数随学习率的减小而增加,这里取条件1(起始值为原始判断矩阵次对角元素,γ=0.100)和条件4(起始值为全1矩阵,γ=0.100)的结果进行分析,其余条件下的结果不再赘述。

条件1下,计算得到的完全一致矩阵如下B7,1所示;条件4下,计算得到的完全一致矩阵如下B7,2所示。

可以看出,选择不同的迭代初值,对最终收敛结果影响较小,以等效完全一致矩阵的改变量为衡量标准,用本文方法计算得到的矩阵总的改变量约为92,最大改变量约为5.3,远小于基本回路法和边界优化法的结果,可见本文方法更能保留原矩阵的信息。

4 结论

本方法通过权重构建一个完全一致矩阵,将其与初始判断矩阵进行拟合,采用梯度下降法求得矩阵调整量最小的完全一致矩阵,最大程度保留了原始判断矩阵信息。该方法在限定最终得到的矩阵为完全一致矩阵的条件下进行,得到的结果同时满足逻辑一致性和数值一致性。而且在计算过程中,不需要反复检验判断矩阵是否满足一致性要求,计算更为便捷。