SEAD场景异构无人机配置与任务规划联合优化方法

王建峰,贾高伟,辛宏博,郭 正,侯中喜

(国防科技大学 空天科学学院, 湖南 长沙 410073)

无人机作为无人系统的“集大成者”,被广泛应用于不同任务场景。大型全能型无人机平台存在任务效费比低、系统容错性差和升级周期长等缺陷[1-2],异构无人机系统旨在将大型平台功能分散到空间分布的低成本单元,通过合理调度实现不同单元的动态组合和密切协作,在兼具经济性的基础上达到甚至超过大型平台能力水平。

对敌防空压制(suppression of enemy air defenses, SEAD)场景是当前异构无人机协同应用的典型场景,受到了广泛关注[3]。当前该场景的研究多在给定无人机配置下进行,并集中于完善场景建模[3-4]与提升求解效率[5]。无人机配置是确定参与任务的无人机类型及数量[6],任务规划是协调各单元以获得执行方案,二者存在递阶关联性,合理的无人机配置可以提升机间协同效率,在满足任务需求的同时避免无人机资源浪费[6]。

SEAD场景中无人机配置和任务规划联合优化问题属于异构车队车辆路径问题(heterogeneous fleet vehicle routing problem, HFVRP)范畴,即寻找最佳异构车队组成和任务路线[7-8]。HFVRP是在车辆路径问题(vehicle routing problem, VRP)的基础上将车队组成也作为变量,较VRP这一NP-hard问题计算复杂度更高。HFVRP包含多种扩展[9-10]——多次访问、站点依赖、时间窗口、资源限制、非对称路径等,本文问题包含类似限制[3,11]:对同一目标顺序执行多种任务;存在时间窗口约束和资源需求;航程和资源载荷有限,且有返航需求;任务执行要求和动力学约束使得任务路径不对称。这些限制极大增加了问题求解难度。

考虑无人机配置对任务执行的影响:文献[12]针对协同搜索与攻击场景,选择不同数量的无人机组合进行仿真,发现增加无人机可以降低任务时间但也增加任务协调成本,数量过多反而降低整体效能;文献[13]针对协同对地打击场景,对比了不同机型组合及数量配置的体系贡献率,发现高速与高隐身无人机体系贡献率较高,无人机数量增加会提高贡献率,但存在饱和。考虑无人机配置与任务规划的递阶关联性,确定合理的无人机配置:文献[14]利用分层策略处理无人机配置与任务分配问题,对比了基于进化算法的同时求解和分层求解的效果,证明了分层策略的有效性;文献[15]针对广域侦察场景,利用聚类方法将目标划分成簇,根据簇群数量确定无人机数量并进行任务指派;文献[16]针对无人机武器配置和打击路径优化问题,设计了基于局部搜索策略的启发式算法,在确定各个目标的毁伤需求的基础上优化无人机任务路径,验证了启发式算法的计算优势。

本文针对SEAD场景特点,建立了异构无人机编队路径问题(heterogeneous UAV fleet vehicle routing problem, HUFVRP)模型,在任务规划问题基础上将各类型无人机数量也作为决策变量,充分表征目标、任务和无人机的多种约束,优化无人机使用数量与任务执行时间指标。建立了双层联合优化方法求解模型:上层调整无人机配置,设计了任务衔接参数引导无人机数量调整;下层求解任务规划,改进遗传算法能够有效处理多种约束,并根据无人机数量变化针对性调整执行方案;双层相互协调以获得无人机配置和执行方案。

1 联合优化问题建模

本节首先介绍SEAD场景想定,然后建立目标、任务和无人机模型,最后给出HUFVRP模型相关数学描述。

1.1 SEAD任务场景想定

场景目标为位置已知的雷达站,毁伤要求和时间窗口已经明确,为简化计算做出如下想定:

1)任务场景为二维区域,不考虑地形障碍、禁飞区、突发威胁等干扰因素,目标和无人机均视为点目标。

2)目标包含多个任务,每个任务由一架无人机执行,不能忽略任务执行时间。

3)无人机存在资源和航程限制,不能无限执行任务,任务完成后需返回起飞点。

1.2 基础模型构建

1.2.1 目标与任务模型

T={T1,…,Ti,…,TNTarget}为目标集合,数量为NTarget。MTi表示目标Ti所属任务集合,包含侦察C、攻击A和评估V三类任务,c∈{1,2,3}为对应类型序号。

MTi⊆{C,A,V}

(1)

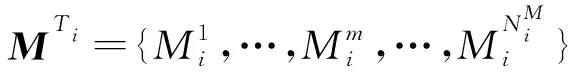
全部任务按照目标序号排列形成任务总集合MAll={MT1,…,MTi,…,MTNTarget},任务总数量为:

(2)

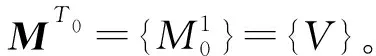
1.2.2 任务耦合关系

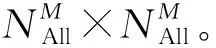
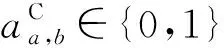
对于某一任务,关联矩阵中对应列的非零项为其依赖的任务,称为前序任务,前序任务全部完成后该任务方可执行;关联矩阵中对应行的非零项为受其影响的任务,称为后续任务,该任务完成后后续任务方可执行。式(3)为侦察、攻击和评估任务的关联矩阵,第3列表示评估任务的前序任务为侦察和攻击任务。

(3)

1.2.3 无人机模型

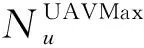
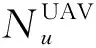
(4)

1.3 问题求解模型

在上述模型的基础上,借鉴异构车队车辆路径问题[7,10]与无人机任务规划[3-4]的部分研究建立HUFVRP模型。定义图模型G(V,A),其中V={T0,T1,…,Ti,…,TNTarget}为起飞点和目标点的集合;A={(i,j)|0≤i,j≤NTarget,i≠j}为无人机目标间转移顺序的集合,(i,j)表示无人机从目标Ti转移至目标Tj。模型相关变量如下:

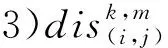
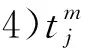
该问题需要寻找合理的无人机配置方案和对应执行方案,因此针对性设置无人机数量F1和任务平均完成时间F2两个优化目标,具体如下:

F1=NUAV

(5)

(6)

模型约束包含任务执行要求、任务时序耦合约束和无人机能力限制三类,建模如下:

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

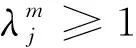
其中:式(7)约束目标包含的任务均分配给无人机执行;式(8)～(9)约束无人机从起飞点出发,执行完任务后返回出发点;式(10)约束无人机按方案顺序执行任务;式(11)确保无人机在任务开始前到达目标位置;式(12)确保任务时间满足时间窗约束;式(13)确保任务时间满足时序耦合约束,其中Y为无穷大值;式(14)确保无人机有能力执行所分配的任务;式(15)确保无人机所执行任务的资源需求不超过其机载资源限制;式(16)确保无人机不超过航程限制;式(17)确保各类无人机使用数量不超过最大数量。

2 双层联合优化方法

2.1 联合优化问题求解分析

无人机配置与任务规划联合优化问题包含多种类型的变量,且变量之间存在递阶关联性,求解十分困难[14]。因此,本文设计了双层联合优化方法,上层进行无人机配置计算,下层进行多无人机任务规划计算,具体见图1。

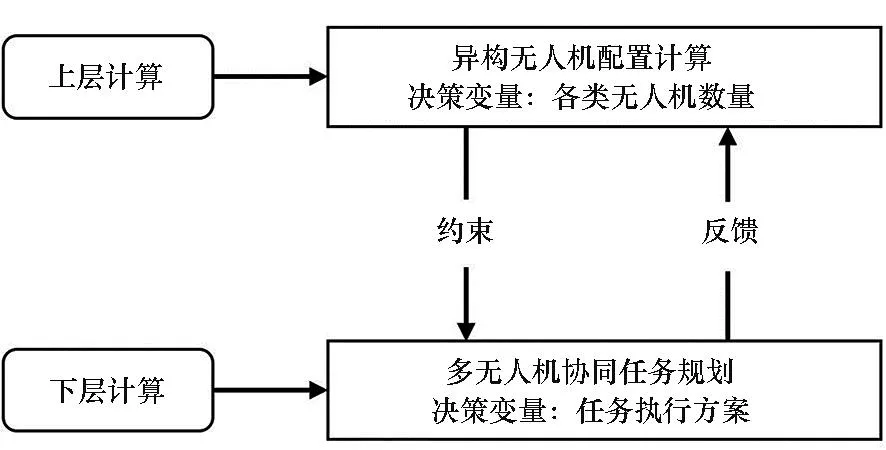
图1 双层联合优化方法结构Fig.1 Structural diagram of the two-level joint optimization method

在上层中,根据任务时间表和无人机使用率设计了任务衔接参数,精确评估各类型无人机需求,指导无人机配置方案调整。在下层中,使用改进遗传算法在给定无人机配置下进行任务规划计算,能结合无人机数量变化精确调整执行方案,在有限时间内能够以更高概率获得高质量执行方案,提升对无人机配置方案的评估准确性。

双层联合优化方法可以通过有限次数的迭代获得满足要求的无人机配置及任务执行方案,避免了无人机配置与任务规划同时求解造成的问题空间非线性扩展,在有限的计算时间内可以获得更高质量结果。

2.2 上层:无人机配置计算

2.2.1 任务衔接参数

(18)

(19)

(20)

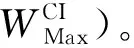
(21)

本文在任务等待时间的基础上设计了任务衔接参数指标δCI,以评估各类型无人机需求情况。某类任务的衔接参数高,说明对应的无人机数量不足,计算如下:

(22)

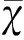
可以根据任务衔接参数的变化判断无人机数量是否饱和:无人机增加会影响对应任务完成时间,进而影响其后续任务的最早允许开始时间。若后续任务对应无人机数量不足,参数将上升;若无人机数量充足,参数将不变,此时不需增加该类无人机。

2.2.2 无人机配置调整流程

无人机配置将在给定的初始配置方案基础上进行调整,每次增加1架无人机,如图2所示,具体流程如下:

图2 无人机配置调整流程Fig.2 Flow chart of UAV configuration adjustment

步骤1：输入初始无人机配置方案。

步骤2：调用下层任务规划,计算当前无人机配置方案下的最优执行方案。

步骤3：根据式(18)～(22)计算任务衔接参数,根据参数对各类型无人机进行倒序排列,形成无人机增加列表。

步骤4：判断各类型无人机是否达到其最大数量限制,若达到则从列表中删除该类无人机。

步骤5：若上次无人机配置迭代时,任务的前序任务对应无人机增加后,该任务衔接参数没有变化,则将对应无人机从列表中删除。

步骤6：选择列表中排在首位的无人机,在当前无人机配置方案的基础上增加1架该类无人机,然后更新无人机配置方案。

步骤7：判断是否满足迭代终止条件,若满足则停止迭代,否则返回步骤2进行计算。

2.3 下层:任务规划计算

下层改进遗传算法主要包含任务编码与调整、任务时间表计算、局部搜索算子三部分,计算流程见图3。

图3 任务规划计算流程Fig.3 Flow chart of mission planning calculation

2.3.1 任务编码与调整

任务编码包含目标序列、任务序列和无人机序列三部分,编码长度与任务总数量相同,按照编码顺序从左至右计算。多层编码情况如图4所示,第一列表示目标T2的攻击任务A由无人机U1执行。

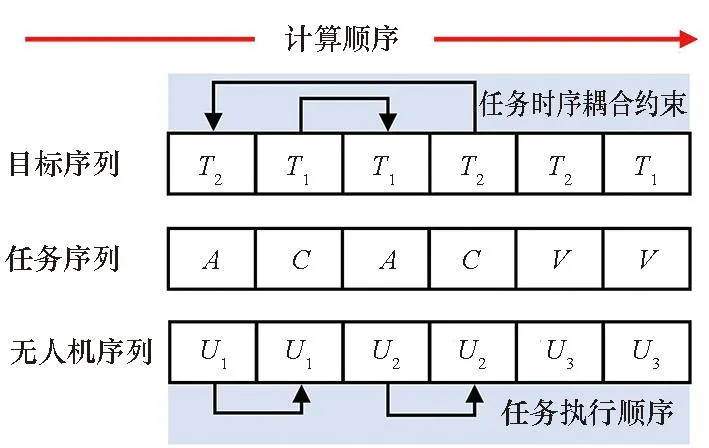
图4 多层编码示意图Fig.4 Multi-layer coding schematic

由于存在时序耦合约束,若某一任务先于其前序任务执行,可能出现“死锁”情况,导致无人机陷入无休止的等待[11]。如图4所示,第1列和第4列分别为目标T2的攻击和侦察任务,任务执行顺序与任务时序耦合约束矛盾,导致前四个任务陷入“死锁”。对此,本文设计了基于任务关联矩阵的“死锁”调整流程,具体如下:

步骤1：在原编码基础上生成空白的新编码。

步骤2：根据编码顺序对原始编码中的任务逐一进行判断——其关联矩阵对应列是否全部为0。

步骤3：若出现任务满足上述条件,则立即停止判断。将该任务从原始编码中删除并将其关联矩阵对应行设为0。

步骤4：将该任务插入新编码的当前第一空位,若编码为空则放置于首位,无人机映射关系不变。

步骤5：判断原始编码是否为空,若是则输出新编码,否则返回步骤2。

该方法只对存在时序耦合约束的任务进行调整,其他任务的对应顺序不变。

2.3.2 任务时间表计算

任务时间表将根据调整后的编码顺序进行计算,每个任务的计算过程包含无人机选择、任务执行路径和任务时间协调三部分。

(23)

2)任务执行路径:采用末端航向松弛的Dubins方法[17]计算任务路径,在满足无人机动力学约束和任务执行需求的基础上,将任务规划寻优和任务路径计算部分解耦,降低整体计算复杂度。计算过程如图5所示,侦察无人机(A点)和攻击无人机(B点)对目标T1和T2执行侦察和攻击任务。蓝色实线为侦察路径:无人机需绕目标盘旋(红色区域)搜集信息,其转移路径为当前位置进入盘旋航线的最短路径,可以使用几何切线方法计算其转移路径,评估任务与侦察任务计算相同。攻击无人机路径为红色实线:无人机需要到达目标上方进行攻击,目标位置将作为无人机转移路径的终点进行计算。

图5 无人机任务路径计算示意图Fig.5 UAV path calculation schematic

3)任务时间协调:根据上述路径可以获得无人机到达时间,然后根据式(18)与前序任务时间和时间窗口进行协调计算任务开始时间。计算完成后需要判断是否满足无人机航程约束,若不满足就选择无人机列表中下一架无人机进行计算,若满足则按照编码顺序计算下一项任务。

2.3.3 局部搜索算子

局部搜索算子将根据无人机配置变化对前序无人机配置下的完成时间较短的方案进行调整。主要将原方案中的部分未完成任务和等待时间较大任务添加至新增无人机执行列表,流程如下:

步骤1：选择一个完成时间较短的任务方案,将其作为基础方案进行调整。

步骤2：选择新增无人机可执行的全部任务,将其中未完成任务和等待时间大于0的任务加入待调整任务列表。

步骤3：为新增无人机增加一个任务——按照待调整任务列表顺序,分别将任务列表中的任务调整至基础方案中新增无人机的执行列表末尾,形成多种新执行方案。

步骤4：计算生成的全部执行方案,选择最优方案。

步骤5：判断最优方案是否优于基础方案,若占优则执行步骤6,否则执行步骤7。

步骤6：将此时最优方案作为基础方案,并从待调整任务列表删除最优方案中已调整的任务,返回步骤3。

步骤7：输出此时的基础方案。

3 场景仿真验证

本节对无人机配置和任务规划联合优化方法进行仿真。分析了无人机配置过程和不同场景下的普适性;验证了任务规划方案的可行性与规划方法的求解效率。

3.1 场景及参数配置

仿真场景区域范围为150 km×150 km,起飞点为[0,0],目标随机分布在[10,140] km×[10,140] km的区域。考虑到任务背景,目标会远离起飞点,因此限制目标与起飞点的最小距离为60 km,目标间最小距离为20 km。目标所属任务集合包含侦察、攻击和评估三个任务。攻击任务存在时间窗口,资源消耗数量为1;评估任务与攻击任务需间隔一定时间以避免烟尘干扰。表1为无人机的性能数据[4]。任务衔接参数中等待时间调节参数为1/3,平均任务数控制系数为0.01。

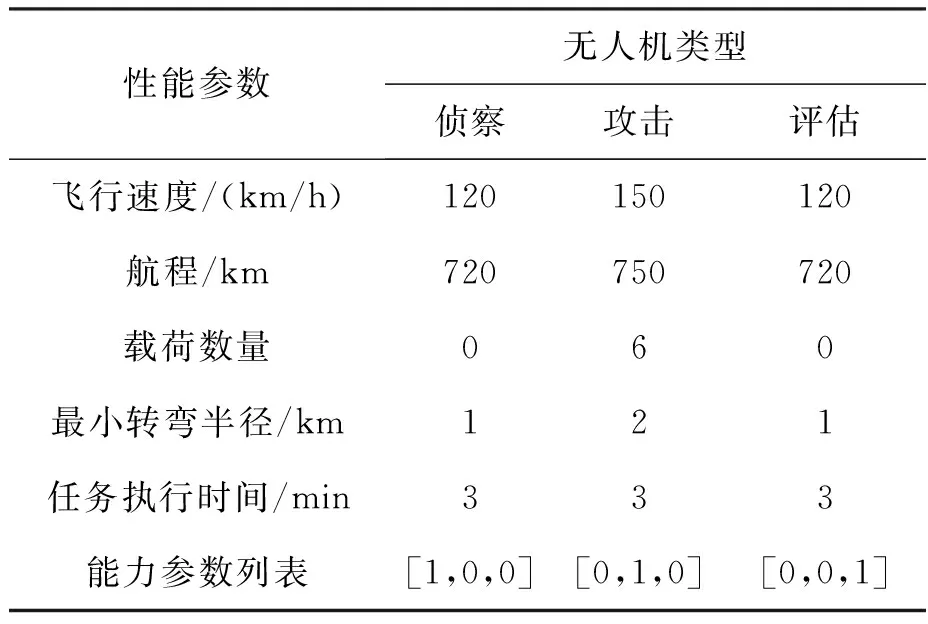
表1 无人机性能数据

3.2 无人机配置方法仿真验证

3.2.1 无人机配置过程分析

场景包含8个目标,初始无人机配置为5架无人机(1侦察、3攻击、1评估),上层无人机配置迭代次数为10。攻击任务时间窗前端分布在[10,30] min,后端分布在[150,180] min,评估任务与攻击任务间隔为1 min。

为验证本文无人机配置方法的有效性,设计了一种对比方法:在迭代时增加衔接参数最小任务所对应无人机,生成一组对比方案。结果如下:

1)无人机配置与任务衔接参数:图6为两种方法的无人机配置方案对比,两种方法的无人机总数量相同,不同类型的无人机数量存在差异。图7表示本文方法的任务衔接参数变化。如图6和图7所示,随着无人机数量增加,任务衔接参数呈下降趋势,第2次迭代时增加了侦察无人机,对应衔接参数下降,其后续的攻击和评估任务的参数上升且变化较大,说明两类无人机数量不足,同样情况也在第4、6、8和9次迭代时出现,但后续任务的衔接参数波动持续减小,说明无人机数量已经较为充足。这表明无人机配置过程中观察无人机增加对任务衔接参数的影响是有意义的。

图6 无人机配置方案对比(左侧为本文方法,右侧为对比方法)Fig.6 Comparison of UAV configuration plans (left is the method in this article, right is the comparison method)

图7 任务衔接参数变化图Fig.7 Chart of connection impact indicator

2)无人机配置与无人机使用率:图8为攻击无人机使用率的变化(其余无人机均全部使用):除初始配置外,本文方法中无人机均全部使用;而对比方法在第2～4次迭代时攻击无人机未全部使用,这是由于无人机比例不合理,侦察无人机数量过少影响侦察任务执行,使得后续攻击任务错过时间窗口,造成攻击无人机资源浪费。在本文方法生成的无人机配置方案中,侦察型多于评估型,攻击型最少。侦察型和评估型无人机性能相同,但侦察任务影响整体任务的执行,故数量较多;攻击无人机速度最快,可以承担更多任务,故数量较少;配置方案与无人机性能参数相符。

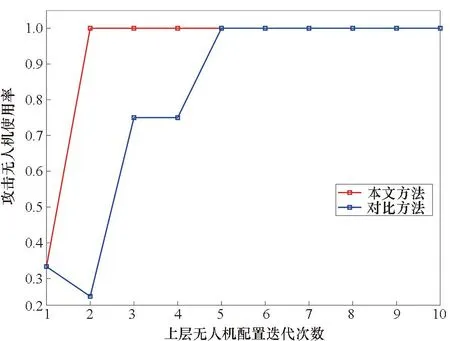
图8 攻击无人机使用率对比Fig.8 Comparison of attack UAV usage rates

3)无人机配置与任务平均完成时间:图9为任务平均完成时间对比,随无人机数量增加,任务平均完成时间持续减小,前期下降快,后期平缓,说明无人机数量增加呈现边际效应。本文方法始终占优,第2次迭代时本文方法中任务已全部完成,但对比方法中存在未完成任务,因此差距较小;迭代后期,两种方法调整基础相同,增加无人机的影响降低,使得差距逐渐减小。

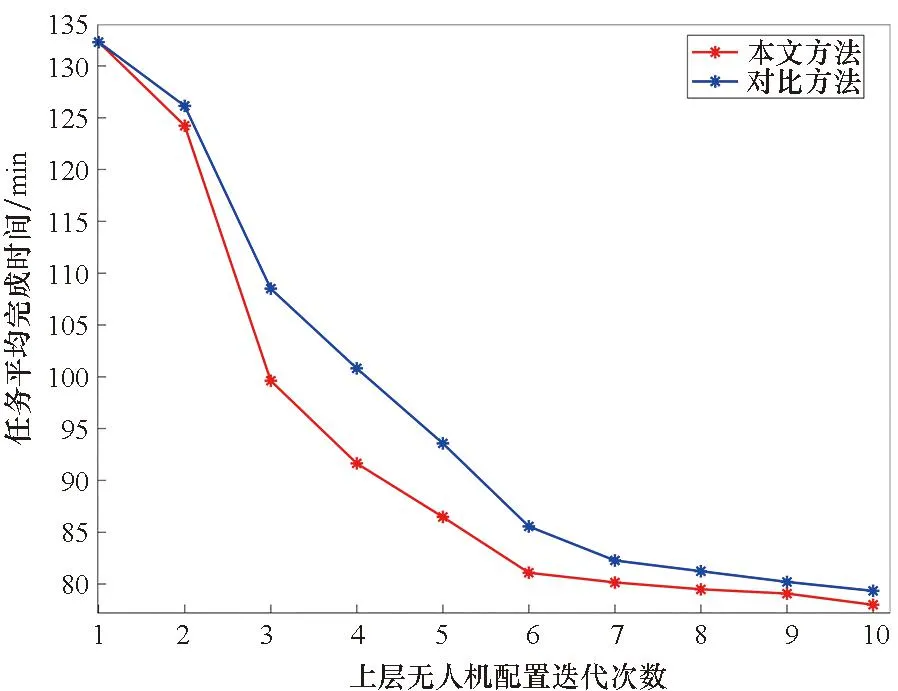
图9 任务平均完成时间对比Fig.9 Comparison of average mission completion time

4)无人机配置与未完成任务:表2为未完成任务情况,图10为未完成数量对比图。在第1次迭代时存在部分攻击和评估任务未完成,本文方法在第2次迭代时增加了侦察无人机,调整后任务全部完成;对比方法增加了攻击无人机,但任务依旧未完成,说明本文方法中分类处理未完成任务的策略是有效的。

表2 未完成任务情况

图10 未完成任务数量对比Fig.10 Comparative chart of uncompleted missions

3.2.2 多场景下无人机配置方法验证

为验证本文方法在不同场景的有效性,进行如下仿真:在目标和任务数量不变的情况下,随机生成100组目标位置和对应时间窗口,在无人机总数量为7～16这十种情况下随机生成无人机配置方案(这一范围内变化明显),运行本文方法和对比方法,对比任务平均完成时间变化。

图11为不同场景下调整后与原方案时间比值的平均值,图中数字为调整前无人机总数量。可以看出本文方法较对比方法始终占优,说明本文方法不同场景中均能够实现对无人机配置的高效调整。在无人机数量为7～9之间时,对比方法的数据存在波动,这是由于此时无人机数量较少且配置方案随机生成,存在部分未完成任务。随着无人机数量增多,增加无人机的积极效果逐渐降低,这与图9中任务平均完成时间的变化趋势相似。

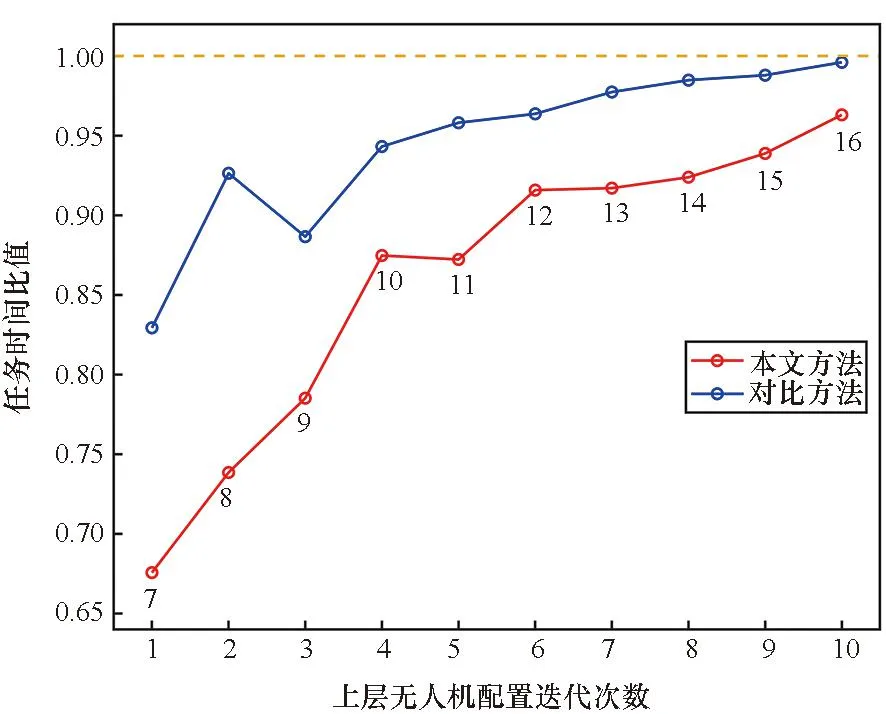
图11 任务时间比值对比Fig.11 Comparative chart of the task time ratio

3.3 多无人机SEAD任务规划仿真验证

3.3.1 任务规划方法可行性分析

选择3.2.1节第5次迭代时生成的任务执行方案进行分析,包含9架无人机(3侦察、3攻击、3评估)。图12为任务执行甘特图,图中序号6-1中6为目标编号,1为任务类型。相同颜色的色块为同一目标任务,粉色色块代表任务执行时间,红色三角表示任务时间窗口。可以看出同一目标的多个任务按顺序执行,满足时序耦合约束;任务均在时间窗口内完成,满足时间窗约束;无人机在留空时间限制内返回出发点,满足航程约束。

图12 任务执行甘特图Fig.12 Mission execution Gantt chart

3.3.2 任务规划方法求解效率分析

为验证本文任务规划方法的求解效率,设置了多种算法进行对比。首先在给定无人机配置方案下分析了算法收敛性能,然后对比不同场景下的算法求解性能。相关算法参数见表3,算法种群数量为100,迭代次数为100。

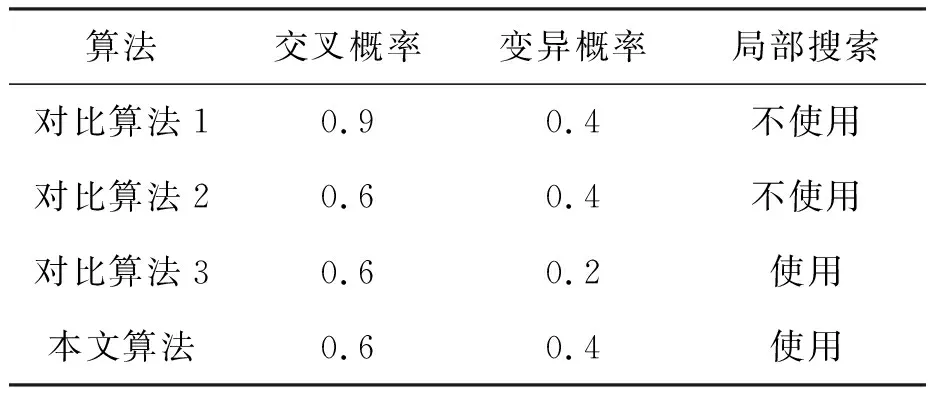
表3 算法参数设置

图13为四种算法在9架无人机(3侦察、3攻击、3评估)时的任务平均完成时间变化,其横坐标为任务规划算法的迭代次数。可以看出,相较于算法1和算法2,本文算法通过增加局部搜索算子,加速了算法收敛并提升了求解质量。本文变异操作主要调整等待时间较长的任务,相较于算法3,本文算法寻优速度更快。

图14为100组场景下的无人机配置调整和任务规划计算:横坐标为上层无人机配置迭代次数,纵坐标为算法最终解与初始最优解的比值,算法使用相同初始种群,比值越小解性能越好。由于第1次迭代时无前序执行方案,无法使用局部搜索算子,故不进行对比。相较于算法1和算法2,由于存在局部搜索算子,本文算法始终占优。计算后期单架无人机承担任务数量较少,局部搜索算子可调整任务数量下降,因此算法之间差异下降。相较于对比算法3,本文算法整体占优但相差很小,与图13中两种算法收敛至相同解的情况相符合,为确保任务规划的求解效果,本文使用了较大的变异概率。

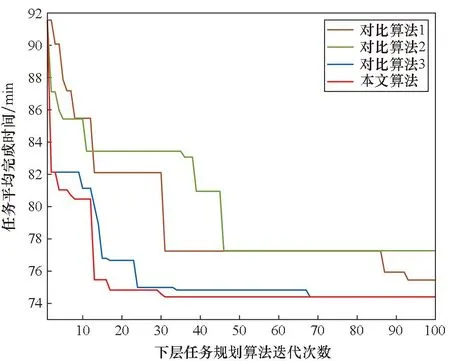
图13 算法收敛性能对比Fig.13 Comparison of the algorithms convergence

图14 多场景下算法效果对比Fig.14 Comparison of the algorithms in multiple scenarios

4 结论

本文针对SEAD场景中无人机配置和任务规划联合优化问题进行研究,在任务规划问题基础上将各类型无人机数量也作为决策变量,充分表征目标、任务和无人机的多种约束,建立无人机编队路径问题模型。设计了双层联合优化方法,将无人机配置与任务规划进行分层处理:上层通过分析无人机数量对任务时间的影响设计了任务衔接参数,评估各类型无人机需求并指导无人机配置调整;下层利用改进遗传算法进行任务规划求解,能够满足多类型约束获得任务执行方案;并设计了局部搜索算子,能够结合无人机数量变化调整执行方案以提升算法寻优效率。

仿真结果表明,无人机数量增加呈现边际效应,合理的无人机配置能够充分发挥各类无人机能力。本文方法能够通过有限次数的迭代获得满足要求的无人机配置及任务执行方案,可以避免无人机配置与任务规划同时求解造成的问题空间非线性扩展,在同等无人机规模下执行方案效果持续占优。该方法为SEAD场景中无人机资源配置与任务规划提供了一套完整的解决方法,可以提高多无人机协同的指控效率。