新能源接入下电网调峰机组负荷优化配置方法研究
2024-04-07冯凯辉宋晨辉宋兆欧
周 倩,汤 林,冯凯辉,宋晨辉,宋兆欧
(1.国网重庆市电力公司,重庆 400000;2.国网重庆市区供电公司,重庆 400000;3.国网能源研究院有限公司,北京 102209;4.国网重庆市北供电公司,重庆 400000)
0 引言
当前,各国家社会经济的发展均离不开能源开发与利用。随着不可再生能源资源的逐步枯竭,能源危机、环境污染问题凸显。为了解决这些问题,需要大力开发与利用可再生清洁能源[1]。我国电力领域正处于能源转型的关键时期,对于电力系统运行的安全性和稳定性的要求逐步提升。随着新能源的开发和接入,电网失稳风险增加。因此,为了提高新能源接入下的电网综合能力,需要针对电网调峰机组负荷优化配置展开研究[2]。
针对这一问题,罗正亮等[3]提出基于改进生物地理学优化-动态规划(improved biogeography-based optimization-dynamic programming,IBBO-DP)模型的水电机组负荷优化分配方法。该方法结合实际情况,搭建IBBO-DP模型,将机组组合是否发生变化作为判断条件,并建立机组出力波动约束;结合IBBO-DP模型,实现机组负荷优化分配。但是该方法并未考虑到其他接入对于机组负荷产生的影响,导致电网风光电发电受阻量较高,实际应用效果不理想。魏文等[4]分析了故障风险类型、负载率水平和天气状况等因素,确定了这些因素对电网调峰机组负荷产生的影响。该方法根据分析结果建立调峰经济模型和风险量化模型,从而确定深度调峰过程中机组的燃料需求和损伤。该方法建立深度调峰经济优化配置模型,以实现负荷优化配置。但是该方法应用后的火电机组和风电场发电出力较低、负荷优化配置效果差,应用效果不理想。刘钢等[5]设计基于深度学习及混沌优化的燃机电站机组热电负荷优化分配方法。该方法以深度学习中的长短时记忆(long short-term memory,LSTM)神经网络为基础,对燃机电站机组能耗进行分析,以获取不同约束参数。该方法采用混沌优化算法对LSTM神经网络模型进行训练,利用训练好的模型进行负荷优化分配。但是在实际应用中发现,该方法由于并未考虑到新能源接入量与电网调峰机组深度调峰之间的关系,使得所建立的目标函数并不合理,负荷优化配置质量下降。王香兰等[6]利用Apriori频繁项集算法,通过分级挖掘分析冷水机组运行参数与最低运行能耗之间的关联规则。该方法根据机组运行总能耗情况建立最优负荷配置目标函数,并利用粒子群算法对目标函数进行求解,以此实现负荷优化配置。但是采用粒子群算法求解目标函数容易陷入局部最优,导致负荷优化配置效果变差。
新能源接入电网会令调峰机组负荷产生较大波动,导致电网调峰机组负荷优化配置难度增加。为了有效解决这一问题,本文设计了新能源接入下的电网调峰机组负荷优化配置方法。该方法重点分析了新能源接入量与电网调峰机组深度调峰之间的关系,解决了传统方法因未考虑该关系使得所建立的目标函数不合理的问题。在此基础上,该方法建立电网调峰机组负荷优化配置目标函数,利用多目标粒子群算法求解目标函数。多目标粒子群算法具有流程简单、收敛速度快、搜索效率高、能够求解多目标优化问题、不容易陷入局部最优等优势,因此所得求解结果具有可靠性和科学性,能够为电网调峰机组负荷优化配置研究与分析提供技术指导。
1 新能源接入量与深度调峰关系
①接入量指标。
本文以电网历史运行的新能源出力数据为基础,根据不同时段计算新能源接入量,并分析不同场景中新能源的接入量特性。
本文设Dy为一个年度中的新能源平均接入量。
(1)
式中:Ei,j为第i天的第j个小时的新能源接入量,kW;m为一天中新能源接入的小时数;n为一年中新能源接入的天数。
本文设Ds为一年某个季度中的新能源平均接入量。
(2)
式中:Es,i,j为某季度第i天的第j个小时的新能源接入量,kW;ns为某季度中新能源接入的天数。
本文设Dm为一个月的新能源平均接入量。
(3)
式中:Em,i,j,k为第k个月的第i天、第j个小时内的新能源接入量,kW;nm为一个月中新能源接入的天数。
本文设Dd为某一天的新能源平均接入量。
(4)
根据上述计算结果,可获得新能源在电网中的接入情况。
②数据分析。
本文设ei,j、ξi,j,k分别为新能源接入量在第i天的第j小时与第k个月的最大值。
(5)
式中:Ep为新能源在电网调峰机组中的总装机容量,kW;h为新能源接入数量。
通过深度调峰可以提升电网调峰能力,进而提高能源在电网中的接入率[7-8]。因此,需要深入分析新能源接入量与电网调峰机组深度调峰之间的关系。本文设Vi,j为新能源接入数据构成的时间序列、Gi,j为深度调峰过程中机组运行时间构成的序列、OVG,i,j为深度调峰时间序列。
(6)
式中:A为深度调峰过程中机组的极限调峰电量,kWh。
当Vi,j、Gi,j的值相等时,表明两者之间存在“与”关系,即OVG,i,j=Vi,j∩Gi,j。
2 电网调峰机组负荷优化配置方法
2.1 目标函数设计
本文考虑新能源接入、风电机组、火电机组在运行过程中产生的相关费用[9-10],将电网调峰机组运行能耗最小化作为研究目标,建立电网调峰机组负荷优化配置目标函数。
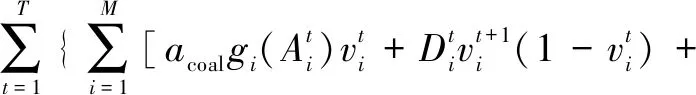
(7)
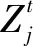
电网调峰机组负荷优化配置目标函数的约束条件如下。
①负荷率约束。
(8)
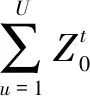
②功率平衡约束。
(9)
③风电机组在电网中的出力约束。
(10)
④火电机组在电网调峰过程中的输出功率约束。
(11)
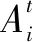
2.2 负荷优化配置实现过程
多目标粒子群算法具有流程简单、收敛速度快、搜索效率高、能够求解多目标优化问题、不容易陷入局部最优等优势。因此,本文采用多目标粒子群算法[11-12]求解上述目标函数,以实现电网调峰机组负荷优化配置。具体过程如下。
①确定电网调峰机组的相关数据。
②设置最大迭代次数tmax、种群数p、粒子在种群中的初始位置x0和速度v0。
③在外部档案Archive中按照顺序加入粒子初始位置x0,并在x0中选取支配解建立初始解集。
④对粒子展开迭代,通过式(12)计算个体在外部档案Archive中的拥挤距离fi′。
(12)
式中:Q为目标数量,个;gi′+1,j′、gi′-1,j′分别为在粒子群中第(i′+1)个和第(i′-1)个粒子对应的第j′个目标值;gj′max、gj′min分别为第j′个目标对应的最大和最小适应度值。
通过轮盘赌策略可以在外部档案Archive中根据粒子的拥挤距离fi′选择最优个体Gbest。
⑤更新粒子对应的速度v和位置x。
(13)
式中:ξ为惯性权重;xi′d,k、xi′d,k+1,vi′d,k、vi′d,k+1分别为第i个粒子在第k次和第(k+1)次迭代过程中生成的第d个位置向量和速度向量;c1、c2分别为两个不同的常数;rand()为随机数;gbest为全局最优位置;pbest为局部最优位置。
⑥针对外部档案,利用非支配解对其展开更新,根据粒子的拥挤距离过滤处理外部档案。
⑦设置多目标粒子群算法的最大迭代次数。如满足条件,则停止迭代。此时,获取式(8)~式(11)的最优解,即负荷率最大、功率最为平衡、风电机组出力以及输出功率最佳。重复上述过程,对目标函数进行求解,以获取电网调峰机组运行能耗最小化目标的最优解。该结果即电网调峰机组负荷优化配置目标函数的最优解。如不满足条件,则引入模糊决策方法获取电网调峰机组负荷优化配置目标函数的最优折中解,从而完成电网调峰机组负荷优化配置。
3 试验与分析
为了验证新能源接入下电网调峰机组负荷优化配置方法的整体有效性,需要对其开展测试。
此次试验设备选用Simulation模拟新能源(风能、太阳能等)。
系统结构如图1所示。
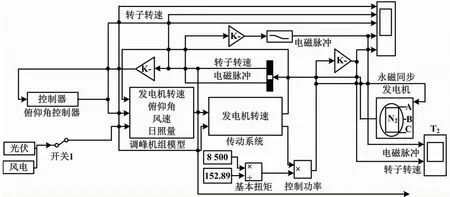
图1 系统结构图
仿真软件与simulation试验电路相连接。通过设置不同的仿真参数模拟单个风力、光伏发电情况。本文将所提方法编辑成相关的执行程序,将不同方法在程序驱动仿真软件中运行,得到所提方法在不同数量风电、光伏发电接入后的控制功率变化曲线。
风电接入后的控制曲线如图2所示。
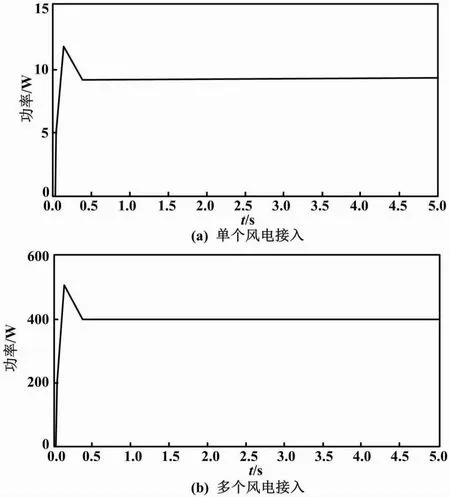
图2 风电接入后的控制曲线
光电接入后的控制曲线如图3所示。
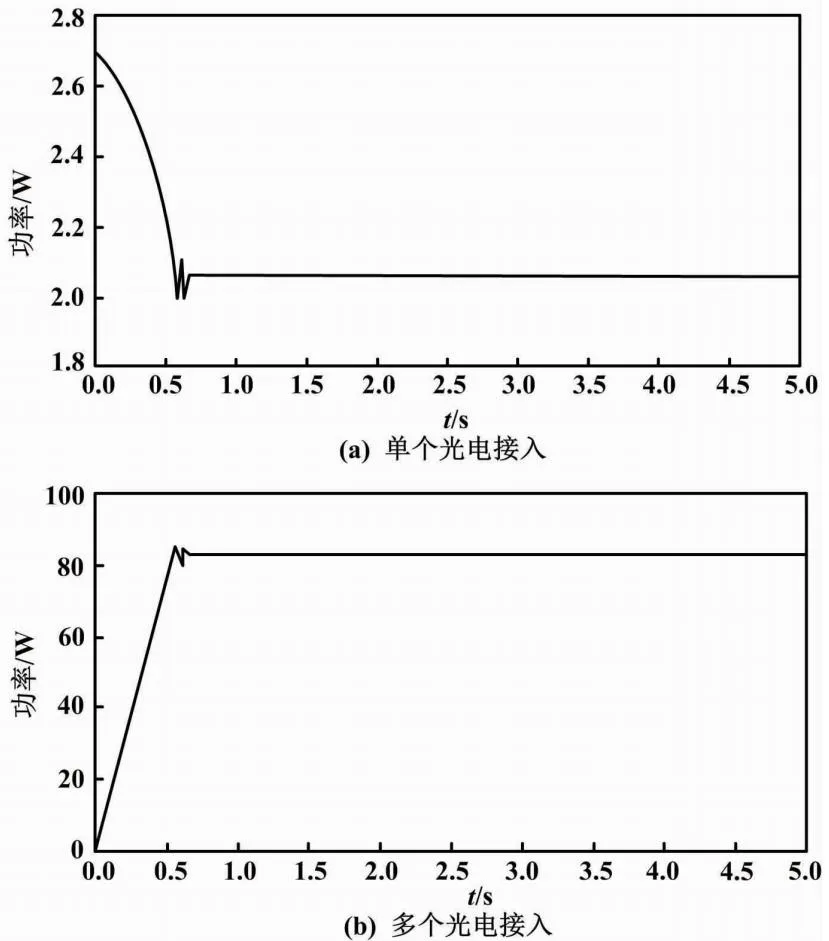
图3 光电接入后的控制曲线
由图2、图3可知,本文方法可以很好地控制接入后的波动情况。在发生波动后,本文方法根据分析结果将优化参数设置为负荷率、功率、风电机组出力、输出功率、电网调峰机组运行能耗。这些系统参数初始值均为0。本文利用多目标粒子群算法求解电网调峰机组负荷优化配置目标函数,以获取目标函数最优解,从而保证电网调峰机组负荷优化配置。
文献[3]方法和文献[4]方法是电网调峰机组负荷优化领域较新、较具代表性的研究成果。因此,试验采用所提方法、文献[3]方法和文献[4]方法对电网调峰机组展开负荷优化配置,以对比不同方法在调峰控制过程中的受阻风电量。
不同方法的风光电发电受阻量如图4所示。
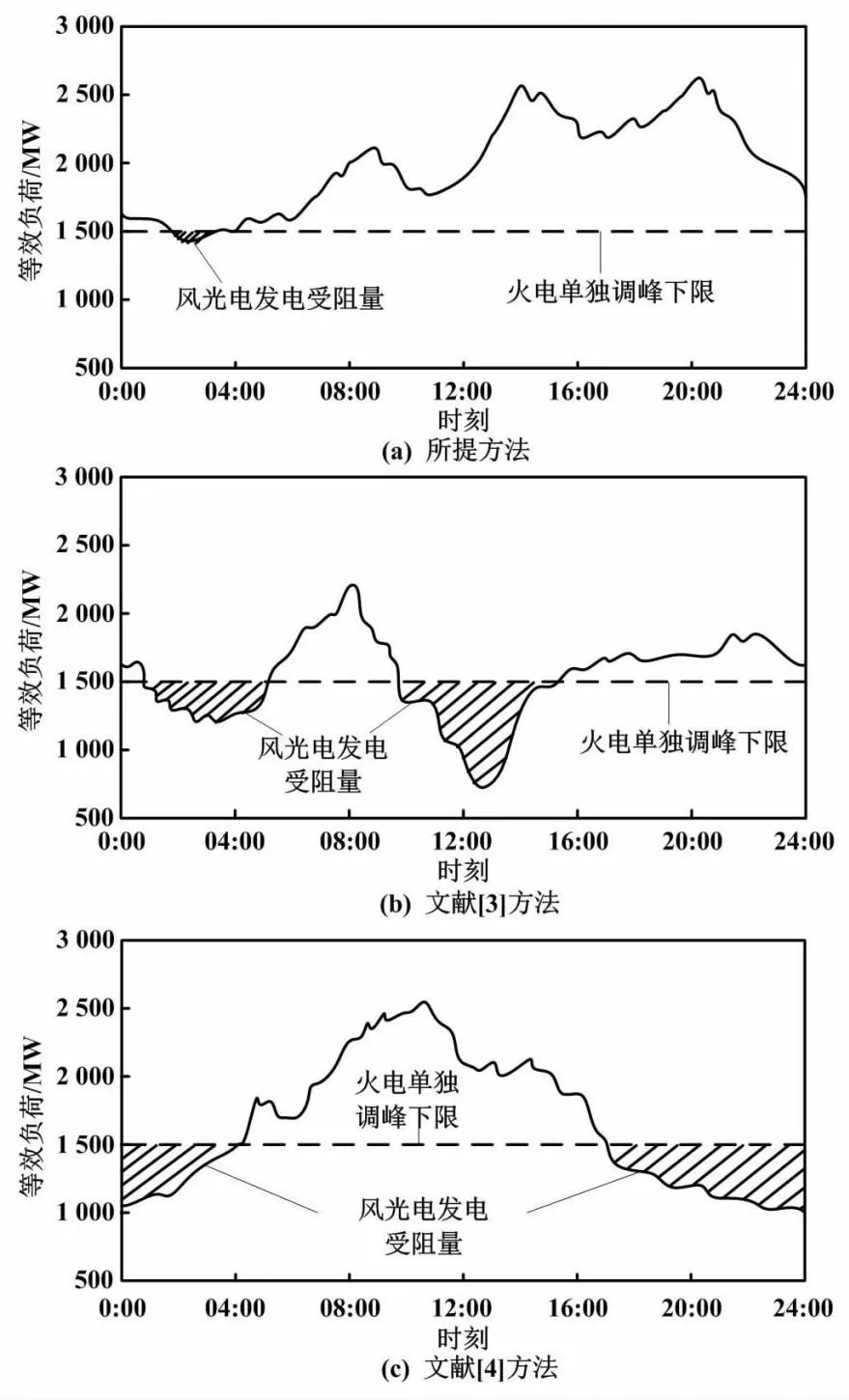
图4 不同方法的风光电发电受阻量
图4中,等效负荷指发电机组实际发出的电量除以发电机组实际应有发电量(能力)的比值。分析图4可知,在调峰机组负荷优化配置初期,所提方法控制电网调峰机组负荷时出现了小部分的风光电发电受阻量。文献[3]方法控制电网调峰机组负荷时,在配置前期和配置中期出现了大量的风光电发电受阻现象。文献[4]方法控制电网调峰机组负荷时,在配置前期和配置后期出现了大量的风光电发电受阻现象。对比三种方法的负荷优化配置结果发现,所提方法的负荷优化配置效果优于另两种方法。
在上述测试环境中,本文将仿真软件与Simulation试验电路建立连接,通过设置不同的参数模拟火电机组和风电场运行情况。试验将所提方法、文献[3]方法和文献[4]方法编辑成相关的执行程序。本文利用不同方法的程序驱动仿真软件运行,以此获取不同方法的火电机组和风电场出力情况。
不同方法的出力情况如图5所示。
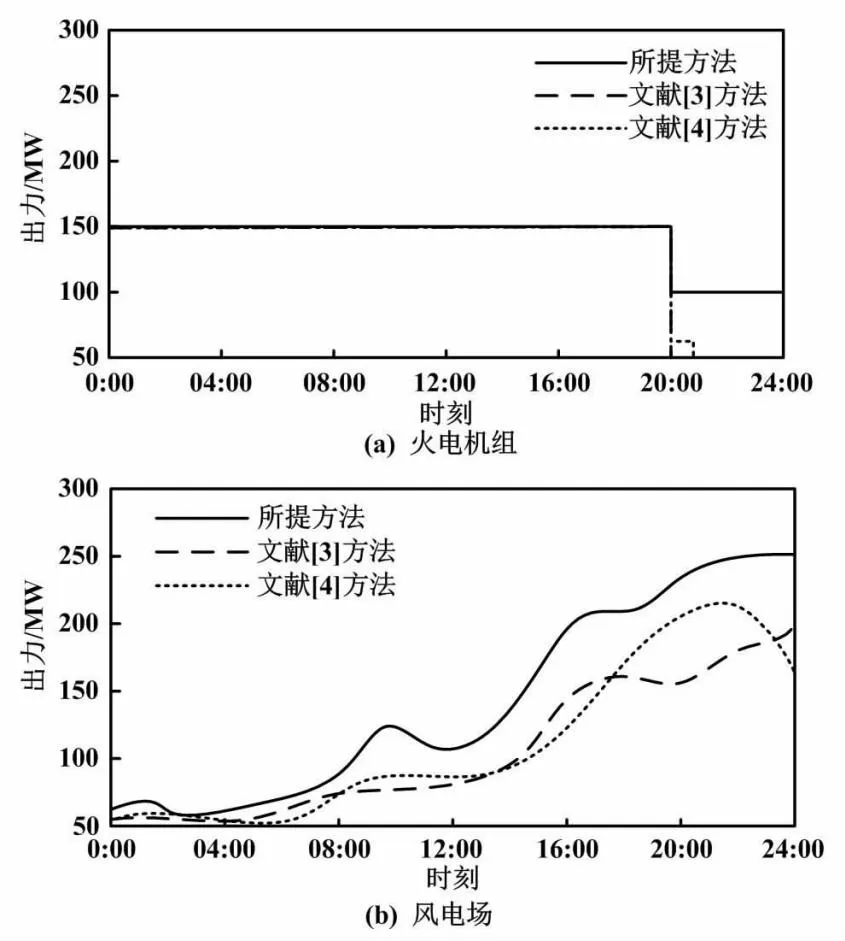
图5 不同方法的出力情况
分析图5可知,在0∶00~20∶00,火电机组在三种方法的控制下均正常运行,且风电场出力不断增高。在20∶00之后,电网的用电负荷有所下降。此时:文献[3]方法和文献[4]方法控制下的火电机组进入停机状态;所提方法控制下的火电机组出力下降至100 MW,并继续出力。通过上述分析可知,所提方法具有灵活的调峰能力。其原因是所提方法在构建电网调峰机组负荷优化配置目标函数之前,考虑了新能源接入问题、分析了新能源接入量与电网调峰机组深度调峰之间的关系,以此实现调峰机组负荷的灵活控制。
不同方法的调峰裕度值如图6所示。
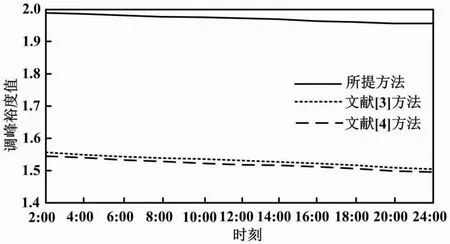
图6 不同方法的调峰裕度值
由图6可知,与其他两种方法相比,所提方法具有较高的调峰裕度值。这表明所提方法具有良好的负荷优化配置效果,可以保证电网运行的安全性和稳定性。
本文将调峰裕度值作为指标,测试三种方法的负荷优化配置效果。调峰裕度值越高,表明负荷优化配置效果越好。
4 结论
当前方法没有考虑到新能源出力在负荷优化配置过程中的波动性和随机性,存在风光电发电受阻量高、出力低和调峰裕度值低的问题。本文提出新能源接入下电网调峰机组负荷优化配置方法。该方法在电网调峰机组负荷优化配置过程中考虑了新能源接入问题。该方法通过建立目标函数实现负荷优化配置,能够有效解决目前方法中存在的问题,具有良好的负荷优化配置效果。
