考虑节能减排的分布式光伏储能容量配置研究
2024-04-07郁丹,吴君,唐人
郁 丹,吴 君,唐 人
(浙江华云电力工程设计咨询有限公司,浙江 杭州 310014)
0 引言
随着智能电网建设水平的不断提高,对于以光电等清洁能源为基础的电网运行稳定性以及电力设备运行节能水平的要求越来越高。近年来,光伏储能技术在智能光电网络建设以及绿色清洁新能源网中的地位越来越高,在节能减排过程中发挥着重要作用[1]。分布式光伏电源的储能功能在很大程度上缓解了能源危机,为保护环境、实现节能减排提供了帮助。但是大规模分布式光伏电源节点接入配电网后,在为光伏行业发展提供便利的同时,因储能不合理造成的浪费使能源损耗上升。在光伏储能成本相对昂贵的市场环境下,需要将不可控电源转化为可控电源,以保证供电质量、减小分布式电源接入的波动性,使分布式光伏储能系统具有更好的应用前景[2]。实际上,光伏电源储能容量的合理配置,能够在降低前期投入的同时,一定程度地控制成本、减少非必要的浪费。但是,分布式光伏电源的工作时间、功耗各不相同,导致其储能非正常损耗较快,不易于大规模存储。一旦分布式光伏储能节点的容量配置不合理,很容易造成能源浪费。因此,分布式光伏储能容量配置问题在新能源推广中受到了众多学者以及电网工作人员的关注。为了维持系统频率和电压的稳定、促进可再生能源的广泛应用,本文考虑节能减排,对分布式光伏储能容量配置方法进行了研究。该研究对提高电能质量具有重要的现实意义。
1 分布式光伏储能容量配置方法
为了完成分布式光伏储能容量配置,使分布式电源持续稳定发挥作用,本文首先建立分布式光伏发电模型,获取分布式光伏电源的参数以及最大功率点输出功率,对光伏发电量进行预测,以保证电网安全与稳定运行;接着计算每日发电供应量和需求量的差值,确定分布式光伏储能容量,并且设定具体的功率支撑条件,以保证储能在突发故障时可以实现快速响应;最后以节能减排为目的设定约束条件以及目标函数,完成分布式光伏储能容量配置,从而提高光伏能源利用率,达到节能减排的目的。
1.1 建立分布式光伏发电模型
分布式光伏发电系统由多块光伏电池板组合而成。为了确定某一段时间内光照幅度的概率分布,需要搭建概率密度函数。该函数的表达式为:
(1)
式中:fu(c)为beta函数;c为一段时间内的太阳辐射强度;γ(·)为Gamma函数;β和α均为beta函数分布的参数[3]。
β和α的计算式为:
(2)
式中:λ为c的平均值;φ为c的方差。
分布式光伏发电的输出功率与光伏阵列组件安装位置的辐射度、温度以及组件参数有关,因此需要计算在c下的最大功率点输出功率。此情况下,组件温度、额定电流、额定电压、功率比以及最大功率点输出功率等参数的计算式如下。
(3)
式中:T为组件温度;Ta为环境温度;T0为标准工作温度;I为组件工作额定电流;IS为组件的短路电流;Ci为电流温度系数;U为组件工作额定电压;Umax为最大功率点处电压;US为开路电压;CU为电压温度系数;f为组件工作功率比;Pmax(c)为最大功率点输出功率;N为分布式光伏电源组件数量。
根据式(3)可得到分布式光伏电源的参数以及最大功率点输出功率,从而实现分布式光伏发电模型的搭建[4]。
1.2 预测光伏发电量
为了使储能容量配置满足大规模、大范围的用电需求,以提高系统的综合性能,需要充分发挥分布式光伏的储能优势,使储能的使用性更灵活。为此,针对分布式光伏发电的随机小扰动和处理波动问题,本文选取研究区域某年全年的光照历史数据作为参照进行光伏出力预测[5]。本文在不同倾斜角幅度条件下,计算光伏发电板的辐射量hx。
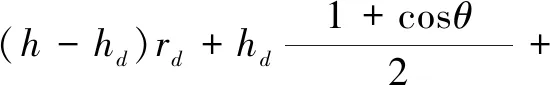
(4)
式中:hd和h分别为水平面的散射量和总辐射量;δ为接收面的反射率;rd为倾斜面与水平面直射量的比值;θ为光电板倾斜角[6]。
(5)
由此预测分布式光伏发电板的发电量为:
(6)
式中:η为转换效率;s为光伏阵列的面积。
通过上述计算,即可获取预测的分布式光伏发电量,从而为解决分布式光伏出力所存在的随机性和不确定性问题提供参考,以保证电网安全与稳定运行。
1.3 储能容量估计
为了保证供电可靠性的同时实现节能减排,确定分布式光伏储能容量非常重要[7]。为了有效实现这一目标,需要计算每日发电供应量和需求量的差值,并根据差值计算结果确定分布式光伏储能容量,从而为后续储能容量配置提供较为可靠的依据。本文根据电网发电量和需求量曲线,计算每日发电量和需求量的差值。
(7)
式中:Pc(i)为第i日的预测光伏发电量能量差;Ps(i)为第i日光伏系统的输出能量;Pm(i)为第i日光伏发电量负荷需求预测结果;P[x=Pc(i)]为第i日预测光伏发电量输出能量正确的概率;pi为第i日的预测正确概率值。
在储能容量选取时,光储系统储能容量估计结果Pr需满足:
Pr∈[qmax,qmin]
(8)
式中:qmax、qmin分别为光储系统储能容量上限与下限。
一般情况下,光储系统储能容量估计结果Pr取值必须满足上、下限要求。为了保证储能在突发故障时可以及时提供功率支撑,需设定具体条件。
PM≥ΔPK
(9)
式中:PM为分布式光伏系统提供的功率;ΔPK为重要负载的最大功率缺失值。
由此能够保证储能大功率充放电在短时间内实现快速响应的效果[8]。
1.4 建立储能容量配置模型
在确定了光伏发电量和储能容量之后,本文需要根据节能减排目标,设置合理的目标函数以及控制变量和约束条件,以实现储能容量配置,保证能源被最大化利用。本文设置控制变量X为储能装置容量的变化量Δq,以q0作为单位容量,通过以下映射关系将离散的变量连续化,以表示储能装置容量。
(10)
式中:qc为单位储能成本。
本文将光伏发电估计量越线概率以罚函数的形式在目标函数中体现,以实现不等式约束的可控。本文经过迭代计算得到目标函数最小时的控制变量,从而得到最优储能装置容量。
(11)
式中:k1为存储容量约束函数;k2为网损系数;Δqloss为光伏系统网损值;Δqc为单位储能成本变化值;ρ为罚函数因子;pVlim为光伏发电估计量越限的最大概率限制值;Umin为电压的最小值;pU为光伏发电估计量越限的基础概率。
Δqloss的计算式为:
(12)
式中:Ui′为节点i′的电压幅值;Uj为辐射量为j时的电压幅值;Mi′j为节点导纳阵元素的实部;vi′j为节点i′的电压相角;Di′j为节点导纳阵元素的虚部[9]。
在不等式约束条件下,本文考虑光伏系统的状态变量约束,将支路功率偏差概率、支路容量均限制在约束范围内。控制变量约束为:
(13)
式中:pl为波动偏差的概率;pllim为极限偏差概率。支路容量约束为:
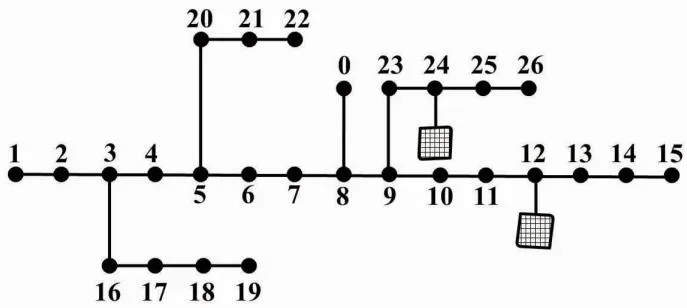
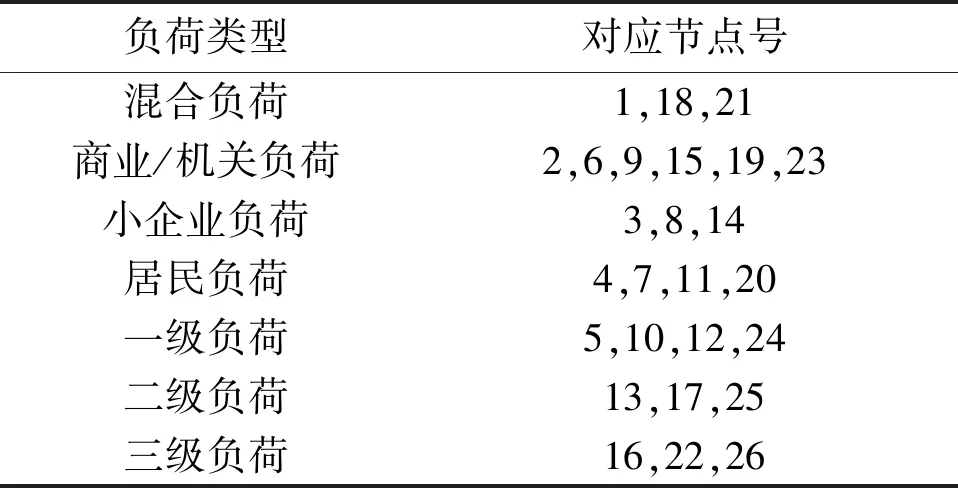
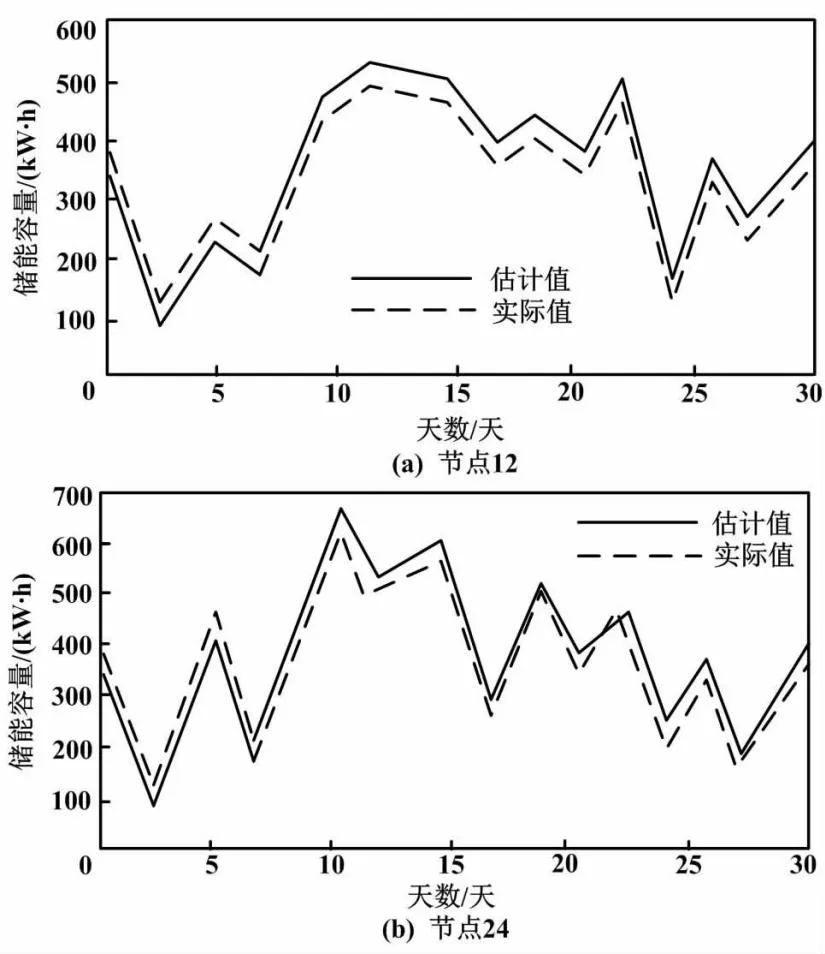
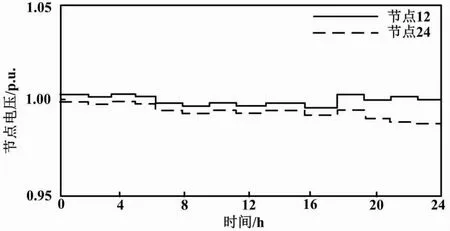
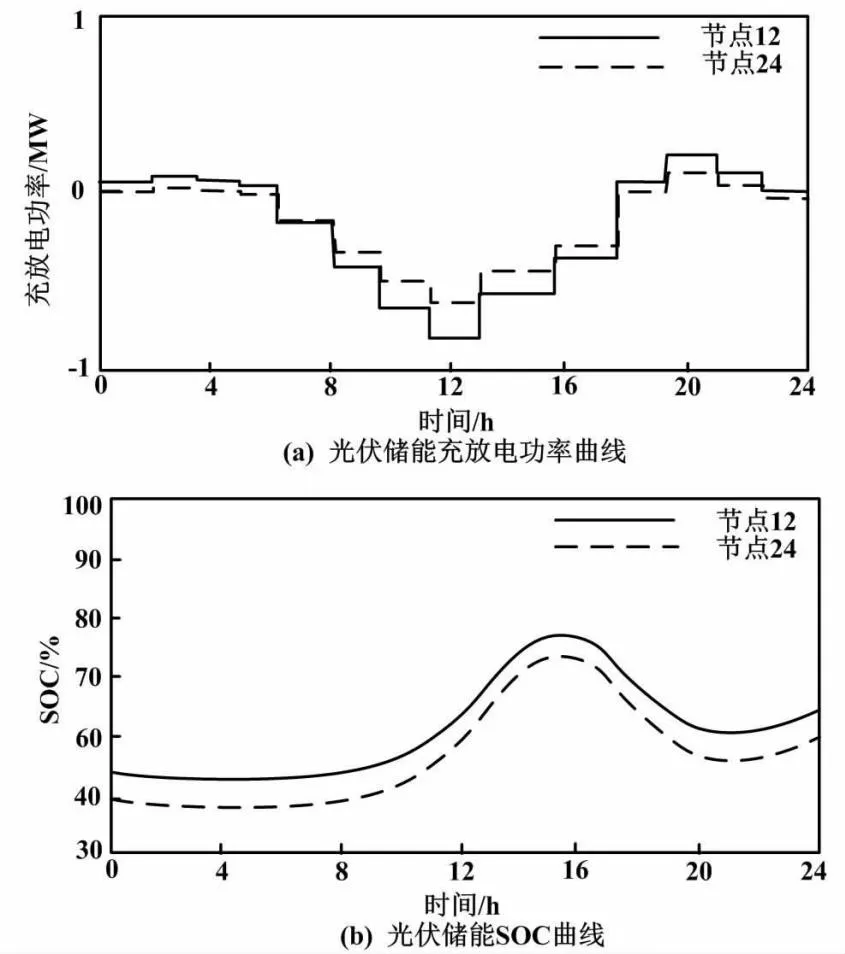
Ei″ (14) 式中:Ei″max为支路i″上的支路容量极限;Ei″为支路i″上的支路容量;m′为光伏系统的支路数量。 经过原始数据的读入,本文初始化迭代次数,计算适应度值后将其限制在约束范围内,并将电压越限概率引入目标函数中。达到最大迭代次数后,本文判断终止条件,并输出结果。记录的最优位置即最优储能容量,以此完成储能容量的配置[10]。 本文选取了某省分布式光伏发电配网系统作为网架结构。该系统中有26个节点。其中:节点0为平衡节点;节点12和节点24均为分布式光伏发电并网节点。 配电节点测试系统结构如图1所示。 图1 配电节点测试系统结构 由图1可知本文测试系统节点位置及数量。其中:节点12和节点24的光伏峰值功率分别为1 200 kW和1 000 kW。 各节点负荷类型如表1所示。 表1 各节点负荷类型 由表1可知各节点负荷类型。本文根据光伏出力特性划分,将节点12和节点24的光伏储能并网点电压划分为3个阶段,设定电池所处的运行区间在0.1~1.0之间。 试验参数设置如下:T=45±3 ℃;Ta=21±12 ℃;To=25 ℃;I=9.75 A;IS=36.91 A;Ci=4.3;U=110 V;Umax=32.26 V;US=24.63 V;CV=4.5;f=3.7;Pmax(c)=13.97 kW;N=12;hx=6 986~7 540 MJ/m2;η=0.7;s=1.745 km2;qmax=600 kWh;qmin=100 kWh;k1=0.86;k2=0.77;Δqloss=12~86 kWh;Δqc=4.56元;ρ=0.36;ρVin=10 Wh;Umin=3.69 V;pV=0.13。 本文利用部分试验参数构建分布式光伏发电模型,将hx、η以及s代入式(7),得到不同日期的光伏发电量预测结果。Pr满足式(8)中Pr∈[qmax,qmin]的约束。结合该结果,本文将k1、k2、Δqloss、Δqc、ρ、plim、Vmin、pV代入式(11),结合式(11)的计算结果进行分布式光伏储能容量配置。 本文试验共分为两部分。第一部分试验对光伏系统处理预测的结果进行验证,以分析本文方法的处理预测效果。在系统真实发电数据中,试验对光伏系统出力情况进行预测,对比实际处理与预测处理结果,评价预测可信度。第二部分试验对容量配置效果进行分析。通过分析系统节点电压曲线、光伏储能充放电功率曲线、光伏储能荷电状态(state of charge,SOC)曲线,可以对本文方法的可行性和合理性进行深入检验,以此分析容量配置效果。 试验使用以下指标对所提方法的分布式光伏储能容量配置效果进行评价。 ①储能容量估算值。 (15) 式中:Pc、Pdc分别为储能系统充电功率、放电功率;εc、εdc分别为储能系统是否充放电的二进制数,取值为0或1;ηc、ηdc分别为储能系统充、放电效率。 ②节点电压。 节点电压指在电路中任意选取一个节点作为参考节点,并令其电压为0后,考虑其余节点与该参考节点之间的电压。其控制性能高,计算简便。电压曲线的波动越平缓,说明电压稳定性越高。 ③充放电功率。 (16) 式中:PB为储能系统充放电功率;PG为交互功率;PL为负荷功率;PPV为光伏电源输出功率;η′为储能系统整体电效率。 ④SOC。 (17) 式中:ΔPr为储能系统的SOC;Prate为储能系统的额定容量。 夏季和冬季为用电高峰期,会出现明显的用电增长。因此,本文选用节点12和节点24发电量为试验数据。节点12发电量为冬季某月全月数据。节点24发电量为夏季某月全月数据。本文将分布式光伏储能容量估计值和实际值进行对比。 容量估计值与实际值对比如图2所示。由图2可知,本文方法的分布式光伏储能容量估计曲线与实际储能容量曲线的变化趋势基本一致,且误差较小。对于节点12,分布式光伏储能容量估计值和实际值对比的最大误差值为48 kW·h。对于节点24,分布式光伏储能容量估计值和实际值对比的最大误差值为56 kW·h。由于天气状况存在较大的随机性,产生了一定的误差。但总体来看,运用本文方法得到的储能容量估计结果仍有价值。其估计结果的可信度较高,能够为后文合理地进行储能容量配置提供较为可靠的依据。 图2 容量估计值与实际值对比 电压幅值标幺值为1.05。本文将全天不同时段的测试系统的节点电压数据和光伏储能运行状态数据进行汇总。 系统节点电压曲线如图3所示。 图3 系统节点电压曲线 图3中电压曲线的波动较为平缓。同时,节点12和节点24均规避了电压越限的风险,证明系统电压稳定,能够保证供电稳定性。 一般情况下,光伏储能充放电功率合理范围在-1~+1 MW内。通常情况下,SOC区间会在中间部分(即30%~80%),出现过充和过放问题的可能性较小。 分布式光伏储能运行状态如图4所示。图4清晰地展示了分布式光伏储能装置的运行状态。在24 h的运行时间中,光伏储能的最大输出功率始终处于合理范围内,避免了过度的电量消耗。SOC也始终在30%~80%这一合理区间内,说明这种情况下分布式光伏储能出现过充和过放问题的可能性较小,以此有效减少了全天的网损电量。全天充放电平衡满足约束条件,达到了节能减排的目的。由此可见,本文方法具有可行性和合理性。 图4 分布式光伏储能运行状态 本文通过构建分布式光伏发电模型,获取分布式光伏电源的参数以及最大功率点输出功率,根据最大功率点输出功率预测光伏发电量。本文在得到光伏发电量预测结果后,将节能减排作为目标,设置分布式光伏储能容量配置的约束条件以及目标函数,完成分布式光伏储能容量配置。经试验论证分析,本文方法的分布式光伏储能容量估计值与实际值相差较小,光伏储能的最大输出功率以及SOC始终处于合理范围内,避免了过度的电量消耗,能够实现节能减排的目标。本文解决了分布式光伏储能系统中如何分配储能容量的问题。通过合理地配置储能容量,可以有效提高光伏发电效率,从而提升能源利用效率和经济效益。因此,本文为清洁能源利用的研究者和实践者提供了借鉴,具有一定的理论和应用价值。未来还将进行复合储能配置的研究,使本文方法更具可靠性和实用性。2 试验论证分析
2.1 试验准备及过程
2.2 光伏储能指标
2.3 光伏系统出力预测结果
2.4 容量配置效果
3 结论
