P-Frobenius问题与p-对称数值半群
2024-04-04应皓天小松尚夫
应皓天 小松尚夫
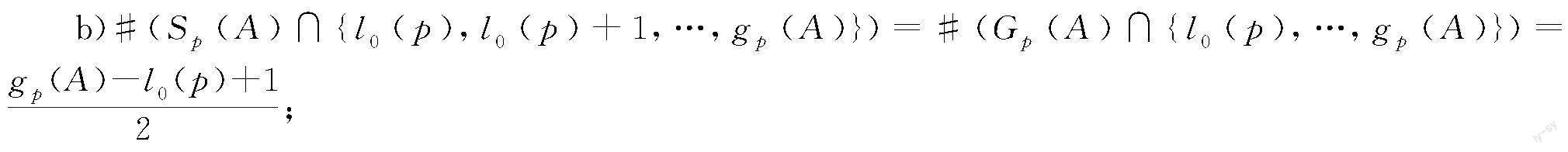
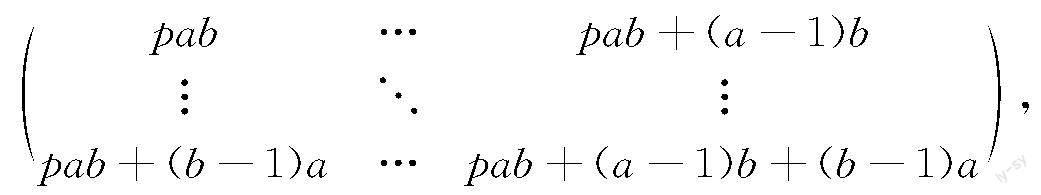
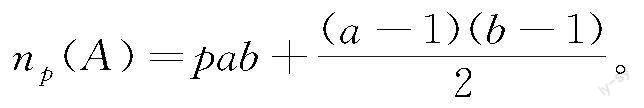
摘 要: 针对p-Frobenius问题中出现的非对称性问题,利用数值半群理论以及Apery集等工具研究了p-Frobenius问题对应的p-对称数值半群。首先利用数值半群和Apery集等工具对p-Frobenius问题进行预处理,得到了对应数值半群和Apery集的各个变量;并将这些变量与对称数值半群和Frobenius问题进行对比,由此定义了p-对称数值半群,并给出了p-对称性的刻画。在此基础上,首先给出了两大类p-对称数值半群,其次研究了对称数值半群与p-对称数值半群的p化关联性。这两类p-对称数值半群给出了大量具体实例,而p化关联性则可用于处理p-Frobenius问题中出现的非对称问题。
关键词: 数值半群;线性丢番图方程;Apery集;对称性;Frobenius问题
中图分类号: O156.7
文献标志码: A
文章编号: 1673-3851 (2024) 03-0265-06
P-Frobenius problem and p-symmetric numerical semigroup
Abstract: In order to deal with the non-symmetry in p-Frobenius problem, we use the theory of numerical semigroup and Apery set to research the corresponding p-symmetric numerical semigroup. We first use the numerical semigroup and the Apery set as tools to get all kinds of variables of the p-Frobenius problem in advance, then we compare these results with the symmetric numerical semigroup and Frobenius problem. Then we can define the p-symmetric numerical semigroup and obtain its properties. On the base of these properties, we find two kinds of p-symmetric numerical semigroup and then research the relationship between the symmetric numerical semigroup and the p-symmetric numerical semigroup. These two kinds of p-symmetric numerical semigroups give lots of examples and the properties can do help to research the non-symmetry in p-Frobenius problem.
Key words: numeical semigroup;linear Diophantine equation; Apery set; symmetry; Frobenius problem
0 引 言
線性丢番图Frobenius问题是数论中的一个经典的古老问题,是由Ferdinand Frobenius于20世纪初提出的。令{a1,…,am}为一组给定的非负整数组,考虑线性丢番图方程a1r1+…+amrm=n是否存在正整数解,其中:n为给定自然数,ri为正整数未知元。当n足够大时,这样的方程一定有正整数解,也称n可由{a1,…,am}表示。Frobenius问题就是寻找不能由该给定的非负整数组所表示的最大自然数的问题,而这个最大自然数则被称为Frobenius数,记为g(a1,…,am)。
Assi等[1]提出,所有可由{a1,…,am}所表示的自然数的集合其实就是一个由{a1,…,am}生成的数值半群,且g(a1,…,am)恰好就是该数值半群的Frobenius数,所以研究Frobenius问题等价于研究一个特殊的数值半群。目前研究数值半群的核心课题之一就是研究对称数值半群,因为所有数值半群都可以进行不可约分解,因此研究一般数值半群的性质可简化为研究不可约数值半群的性质,而不可约数值半群一定是对称数值半群或拟对称数值半群。以上分解可参见Rosales等[2]文献。
在Frobenius问题的基础上,进一步考虑解的数目,Komatsu[3]研究了推广的p-Frobenius数。令{a1,…,am}为一组给定的非负整数组,考虑可由{a1,…,am}所表示且其表示方法至少有p种的自然数所组成的集合,称该集合为p化数值半群。该p化数值半群的Frobenius数被称为p-Frobenius数,其恰好等于不能被至少p种{a1,…,am}所表示的最大自然数,而这样的问题被称为p-Frobenius问题。研究Frobenius问题及其对应数值半群,一般会先对对应数值半群进行不可约分解,再研究该数值半群的对称性。然而事实上,对称数值半群在p化后得到的p化数值半群却不一定保持对称性,因此难以利用以往的对称数值半群相关性质来研究和分解一般的p化数值半群。
为了研究p化数值半群的的不对称性,本文利用数值半群与Frobenius问题的密切联系,以及Apery集等工具研究p化数值半群,将对称数值半群的定义进行了p化推广,从而定义p-对称数值半群并研究了其相关性质。在此基础上,给出了两类p-对称数值半群,并得到对称数值半群与p-对称数值半群的p化关联性。这两类p-对称数值半群给出了大量具体实例,而p化关联性可解决p-Frobenius问题中出现的难以处理的非对称问题。
1 p-对称数值半群的定义及其性质
1.1 p-对称数值半群的定义
给定一组非负整数A={a1,…,am}且a1<… 一个数值半群S(A)被称为是对称的,如果它满足:对一切不属于S(A)的整数x有g(A)-x∈S(A)。 对每个k∈S(A)*S(A)\{0},定义k相关Apery集为: Ape(S(A);k){s∈S(A)|s-kS(A)}={m0,m1,…,mk-1}。 其中:mi为S(A)中满足mi≡i(modk)的最小元素;第一个等号后为Apery集的第一种定义;第二个等号后为第二种定义。以上两种定义等价,详细证明可参见文献[4]。由第二种定义,显然Ape(S(A);k)恰好含有k个元素;特别地,令k=a1时,记Ape(Sp(A);a1)中最小的元素为l0(p)。 一个p化数值半群Sp(A)被称为是p-对称的,如果它满足:对一切不属于Sp(A)的整数x有l0(p)+gp(A)-x∈Sp(A)。注意到当p=0时有l0(p)=0,所以p-对称数值半群包含了对称数值半群,是对称数值半群的p化推广。 例1 令A={3,10,17},则S1(A)={20,23,26,27,29,30,32,33,…},其中…表示之后的整数都属于S1(A)。故l0(1)=20,g1(A)=31,由定义易知S1(A)是1-对称的。S2(A)={30,33,36,37,39,40,42,43,…},故l0(2)=30,g2(A)=41,由定义易知S2(A)是2-对称的。S3(A)={40,43,46,47,49,50,…},故l0(3)=40,g3(A)=48,由于44S3(A)且44+44=88= l0(3)+g3(A),故S3(A)不是3-对称的。 1.2 p-对称数值半群的性质 令Gp(A)为所有不属于Sp(A)的整数的集合。由p-对称数值半群的定义显然有: 引理1 给定一个p化数值半群Sp(A),以下条件等价: a)Sp(A)是p-对称的; c)若x,y为非负整数且满足x+y=l0(p)+gp(A),则x,y其中一个属于Sp(A)而另一个属于Gp(A)。 证毕。 定理1 p化数值半群Sp(A)是p-对称的,当且仅当2d1=d2。 证毕。 对于给定的一组非负整数A={a1,…,am}且a1<… 证明 Punyani等[7]给出了以下用k相关Apery集中元素表示的Sylvester数公式: 对于p-Sylvester数,利用a1相关Apery集Ape(Sp(A);a1)中元素可得: 等號两边同乘2,并将右边的第一项求和中的mpi重新排序组合后求和,可得: 最后等号两边同除2。 证毕。 2 两类p-对称数值半群及其p化关联性 本节将给出两大类p-对称数值半群,并研究这两类p-对称数值半群与其初始数值半群之间的p化关联性。首先,采用标准表示研究二元情形下的一类p-对称数值半群及其p化关联性,然后利用定理2来研究三元特殊情形下的一类p-对称数值半群及其p化关联性。 2.1 二元情形 不妨设a 引理3 对于n的标准表示n=ax0+by0有: a)0≤y0≤a-1; b)对于任意整数n∈S(A),n∈Sp(A)当且仅当x0≥pb。 证明 a)如若不然,则y0<0或y0≥a。y0<0不满足方程n=ax+by(y≥0)中y的要求,而y0≥a时x不是最大所求整数。故假设不成立因此0≤y0≤a-1。 b)先证明充分性。如若不然,则有n=ax0+by0且x0 再证明必要性。由x0≥pb,n=ax0+by0=a(x0-b)+b(y0+a)=…=a(x0-(p-1)b)+b(y0+(p-1)a)=a(x0-pb)+b(y0+pa),则n至少有p+1种表示,故n∈Sp(A)。 证毕。 定理3 对一切非负整数p,给定A={a,b}且a,b互素,则Sp(A)是p-对称的。 证明 由引理3,Sp(A)中最小元素为pab且其后ab-1个元素可按如下排列: 其中纵向逐行增加a,横向逐列增加b。注意到从pab+ab-a-b+1开始,所有整数都属于上述排列,故属于Sp(A)。由定义易得gp(A)=pab+ab-a-b。 此外,在此情形下有k=a1=a,故由定義知l0(p)=pab。 由Komatsu等[8]的结果,有以下关于二元情形的p-Sylvester数公式: 故有gp(A)+l0(p)+1=pab+ab-ab-pab+1=2pab+(a-1)(b-1)=2np(A),由定理2知,此时Sp(A)是p-对称的。 证毕。 特别地,由Assi等[1]可知,A={a,b}且a,b互素时,对应数值半群S(A)都是对称的,故有以下关于对称数值半群与p-对称数值半群的p化关联性的推论: 推论1 对于二元情形A={a,b}且a,b互素,所有对称数值半群S(A)在p化后变为p-对称数值半群Sp(A)。 2.2 三元等差数列情形 对于高维一般情形,无论是Frobenius问题还是对应数值半群,相关研究都十分困难,目前许多文献都研究一些特殊情形下的性质,如Marin等[9]研究了Fibonacci数列情形,Robles-Prez等[10]研究了三角形和四面体情形,Rosales等[11]研究了纯元数组情形。本节主要研究三元等差数列情形,先给出一类p-对称数值半群,再研究其p化关联性。 定理4 令a为大于等于3的偶数,d为大于0的整数且a,d互素,A={a,a+d,a+2d},则当p=a/2-1时Sp(A)是p-对称的。 证明 由l0(p)的定义可知,当a为偶数,p=a/2-1时,l0(p)=2p(a+d)。此外,Robles-Prez等[12]给出了三元等差数列情形下关于p-Frobenius数和p-Sylvester数的公式: 其中:[]表示取整。 证毕。 特别地,由Binner[13]知,a为偶数,d为大于0的整数,且a,d互素,A={a,a+d,a+2d}时,此时数值半群S(A)是对称的,故有以下推论: 推论2 令a为大于等于3的偶数,d为大于0的整数且a,d互素,A={a,a+d,a+2d},则当p=a/2-1时,对称数值半群S(A)在p化后是p-对称的。 此外,当p=a/2-1时,难以求得l0(p),故无法利用上述方法考察Sp(A)的p-对称性及其p化关联性,但是通过计算和计算机辅助考察了许多例子后发现,Sp(A)也是p-对称的。而且这种情况不仅存在于三元等差数列情形,经实验还发现,一般的高维对称数值半群在p化后仍保持p-对称,故本文猜测,一切对称数值半群在p化后是p-对称的。 3 结 论 本文利用数值半群理论以及Apery集等工具,研究了p-Frobenius问题以及p-对称数值半群。通过链长度和Sylvester数等数值半群不变量,给出了p-对称数值半群的两种等价刻画,并以此为基础研究了二元情形与三元等差数列情形,找到了两大类p-对称数值半群。在这两种特殊情形下证明,对称数值半群在p化后会变为p-对称数值半群;但对一般的高维情形,难以给出严格的数学证明。在这些基础之上,可继续研究一些特殊的情形,发现更多的p-对称数值半群及其性质,以助于研究一般高维情形的p-对称性。 参考文献: [1]Assi A, D'Anna M, García-Snchez P A. Numerical Semigroups and Applications[M]. Cham: Springer International Publishing, 2020:138. [2]Rosales J C, Garcia-Sanchez P A. Numerical Semigroups[M]. New York: Springer-Verlag, 2009:181. [3]Komatsu T. On the number of solutions of the Diophantine equation of Frobenius-general case[J]. Mathematical Communications, 2003,2(8):195-206. [4]Apery R. Sur les branches superlineaires des courbes algebriques[J]. Comptes Rendus Hebdomadaires Des Seances De L Academie Des Sciences, 1946, 222(21):1198-1200. [5]Watanabe K. Some examples of one dimensional Gorenstein domains[J]. Nagoya Mathematical Journal, 1973, 49: 101-109. [6]Kunz E. The value-semigroup of a one-dimensional Gorenstein ring[J]. Proceedings of the American Mathematical Society, 1970, 25(4): 748-751. [7]Punyani P, Tripathi A. On changes in the Frobenius and Sylvester numbers[J]. Integers, 2018, 18B: A8. [8]Komatsu T, Zhang Y. Weighted Sylvester sums on the Frobenius set[J]. Irish Mathematical Society Bulletin,2021, 87: 35-44. [9]Marin J M, Alfonsín J L, Revuelta M P. On the Frobenius number of Fibonacci numerical semigroups[J]. Integers, 2007(14A): 7-13. [10]Robles-PrezA M, Rosales J C. The Frobenius number for sequences of triangular and tetrahedral numbers[J].Journal ofNumber Theory, 2018, 186: 473-492. [11]Rosales J C, Branco M B, Torro D. The Frobenius problem for repunit numerical semigroups[J]. The Ramanujan Journal, 2016, 40(2): 323-334. [12]Robles-Prez A M, Rosales J C. The Frobenius problem for numerical semigroups with embedding dimension equal to three[J]. Mathematics of Computation, 2012, 81(279): 1609-1617. [13]Binner D S. The number of solutions to ax+by+cz=n and itsrelation to quadratic residues[J]. Journal of Integer Sequences, 2020, 23:206-225.
