卧式单轴捏合反应器结构对流体流动与混合特性的影响
2024-04-04杨立森张先明
杨立森 张先明

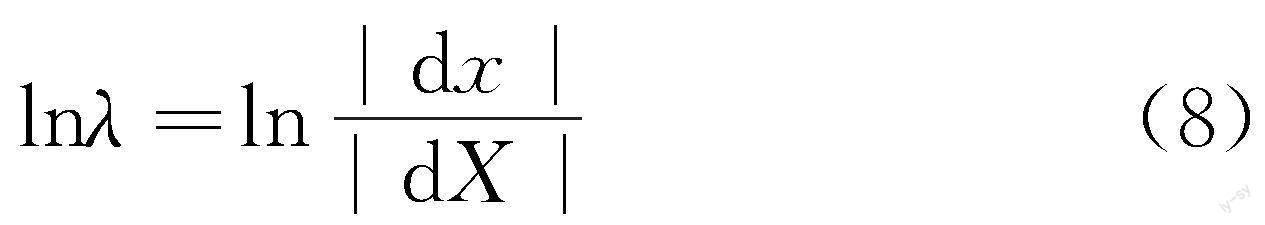
摘 要: 為进一步分析卧式单轴捏合反应器内流体流动与混合特性,采用有限元方法与粒子示踪技术,通过数值模拟方法研究了高黏牛顿流体在不同结构卧式单轴捏合反应器内的流动与混合过程。首先,采用有限元方法对不同结构反应器内流体流动过程进行模拟,以分析反应器结构变化对流体速度分布、剪切速率分布和混合指数分布的影响规律;然后,采用粒子示踪技术对不同结构反应器内流体混合过程进行分析,以探究反应器结构变化对流体分布混合过程、拉伸率及混合效率的影响规律。结果表明:分布混合的实验结果与数值模拟结果吻合较好;高速度、高剪切区域的面积随捏合杆侧边长度的增加而增大;反应器内混合指数分布大于0.7所占的比例,随静态捏合杆数目和捏合杆侧边长度的增加而先增大后减小;增加静态捏合杆数目有利于强化分布混合过程;平均对数拉伸率随静态捏合杆数目和捏合杆侧边长度的增加而增大;平均时均混合效率随静态捏合杆数目的增加而先增大后减小,随捏合杆侧边长度的增加而增大。该研究得到的反应器结构变化对流体流动与混合特性的影响规律,可为卧式单轴捏合反应器的优化设计提供理论指导。
关键词: 单轴捏合反应器;数值模拟;反应器结构;分布混合;混合效率
中图分类号: TQ320.5
文献标志码: A
文章编号: 1673-3851 (2024) 03-0161-13
Influence of the structure of horizontal single-shaft kneader on fluid flow and mixing characteristics
Abstract: To further study the fluid flow and mixing characteristics in the horizontal single-shaft kneader, the finite element method (FEM) and particle tracer technique were combined to study the flow and mixing processes of highly viscosity Newtonian fluid in a horizontal single-shaft kneader with different structures by numerical simulation. Firstly, the FEM was used to simulate the flow process of fluid in kneader with different structures, so as to analyze the influence of kneader structure changes on the fluid velocity distribution, shear rate distribution and mixing index distribution. Then, particle tracer technology was used to analyze the mixing process of fluid in kneader with different structures, so as to explore the influence of kneader structure changes on the fluid distributive mixing process, length of stretch and mixing efficiency. Results show that the experimental results of distributive mixing are in good agreement with the numerical simulation results; the area of high velocity and shear region increases with the increase of kneading bars side length; the proportion of mixing index distribution greater than 0.7 in the kneader firstly increases and then decreases with the increase of the number of static kneading bars and the length of kneading bars; increasing the number of static kneading bars is beneficial to strengthening the distributive mixing process; the average length of stretch increases with the number of static kneading bars and the side length of kneading bars; the average time average mixing efficiency firstly increases and then decreases with the increase of the number of static kneading bars, and increases with the increase of the length of the side of the kneading bars. The influence law of kneader structure changes on fluid flow and mixing characteristics obtained can provide theoretical guidance for design and optimization of horizontal single-shaft kneaders.
Key words: single-shaft kneader; numerical simulation; kneader structure; distributive mixing; mixing efficiency
0 引 言
聚合反应过程通常具有高黏、变黏的特性,高黏度聚合物熔体的混合是制备和加工聚合物的重要步骤之一。双螺杆挤出机和卧式单轴圆盘反应器已广泛用于聚合物的制备和加工。双螺杆挤出机具有自清洁效果和捏合作用,但反应空间较小;相比之下,卧式单轴圆盘反应器具有较大的反应空间,但几乎没有捏合作用和自清洁效果[1-3]。为解决该问题,瑞士List公司通过周期性捏合反应器内桨叶上旋转的捏合杆与壁面上固定的捏合杆来强化混合过程,设计了一系列具有较大反应空间的单轴自清洁设备。该系列设备已成功应用于聚合物脱挥、蒸发、聚合等过程[4],但国内对相关设备的研究报道较少。
近30年来,卧式单轴反应器的研究得到了一定的发展[5]。在实验研究方面,马青山等[6]以烯烃气相聚合卧式单轴搅拌反应器为研究对象,考察了转速、装料量、粉体密度等因素对搅拌功率的影响规律,拟合了粉体搅拌的功率准数关联式。Fleury[7]提出了一种新型卧式单轴捏合反应器,并在反应器中进行了甲基丙烯酸甲酯的自由基聚合实验,对得到的实验数据进行分析,确定了在给定聚甲基丙烯酸甲酯分子量的情况下引发剂和链转移剂的最佳浓度。尽管实验研究可以精准考察所研究设备的操作参数与性能参数间的关系,但反应器内的流动、传热、混合等特性难以完全依靠实验方法来获得,因而获得的影响规律难以用于设备优化和放大过程。计算流体力学(Computational fluid dynamics, CFD)方法则可以有效获取反应器内的流动、传热、混合等特性[8]。王嘉骏等[9]采用CFD方法,通过数值模拟研究卧式单轴格子桨搅拌槽内监测点处示踪剂浓度达到整个搅拌槽内的平均浓度所需的混合时间,发现转速是影响混合时间的关键因素。罗彬彬[10]结合动网格技术与多相流模型,研究了不同黏度流体下重力对卧式单轴自清洁釜内气液分层流流场的影响,并考察了搅拌转速、物料流动速度等因素对釜内平均对流传热系数的影响规律。单纯[11]基于滑移网格技术和RNG k-ε湍流模型对卧式单轴自清洁搅拌釜的流场进行数值模拟,研究发现搅拌釜内高速度区域的面积随搅拌转速增大而增大,物料的停留时间受搅拌翅螺旋角大小、搅拌转速等因素影响。目前反应器结构变化对卧式单轴捏合反应器内流体流动与混合特性影响的研究较少。
有限元方法(Finite element method, FEM)适用于计算复杂结构装置的混合过程,很多捏合反应器和螺杆挤出机的数值模拟研究表明该方法适用于研究反应器的混合过程[12-14]。本文采用有限元方法和粒子示踪技术,模拟了不同结构卧式单轴捏合反应器内高黏牛顿流体的流动与混合过程,并通过分布混合实验对数值模拟的可靠性进行验证。首先利用有限元方法探究反应器结构对反应器内流体速度分布、剪切速率分布和混合指数分布的影响,然后通过粒子示踪技术考察反应器结构对反应器内流体分布混合过程、拉伸率及混合效率的影响。本文研究反应器结构变化对流体流动与混合特性的影响规律,期望对卧式单轴捏合反应器的优化设计提供一定的理论指导。
1 卧式单轴捏合反应器的几何结构
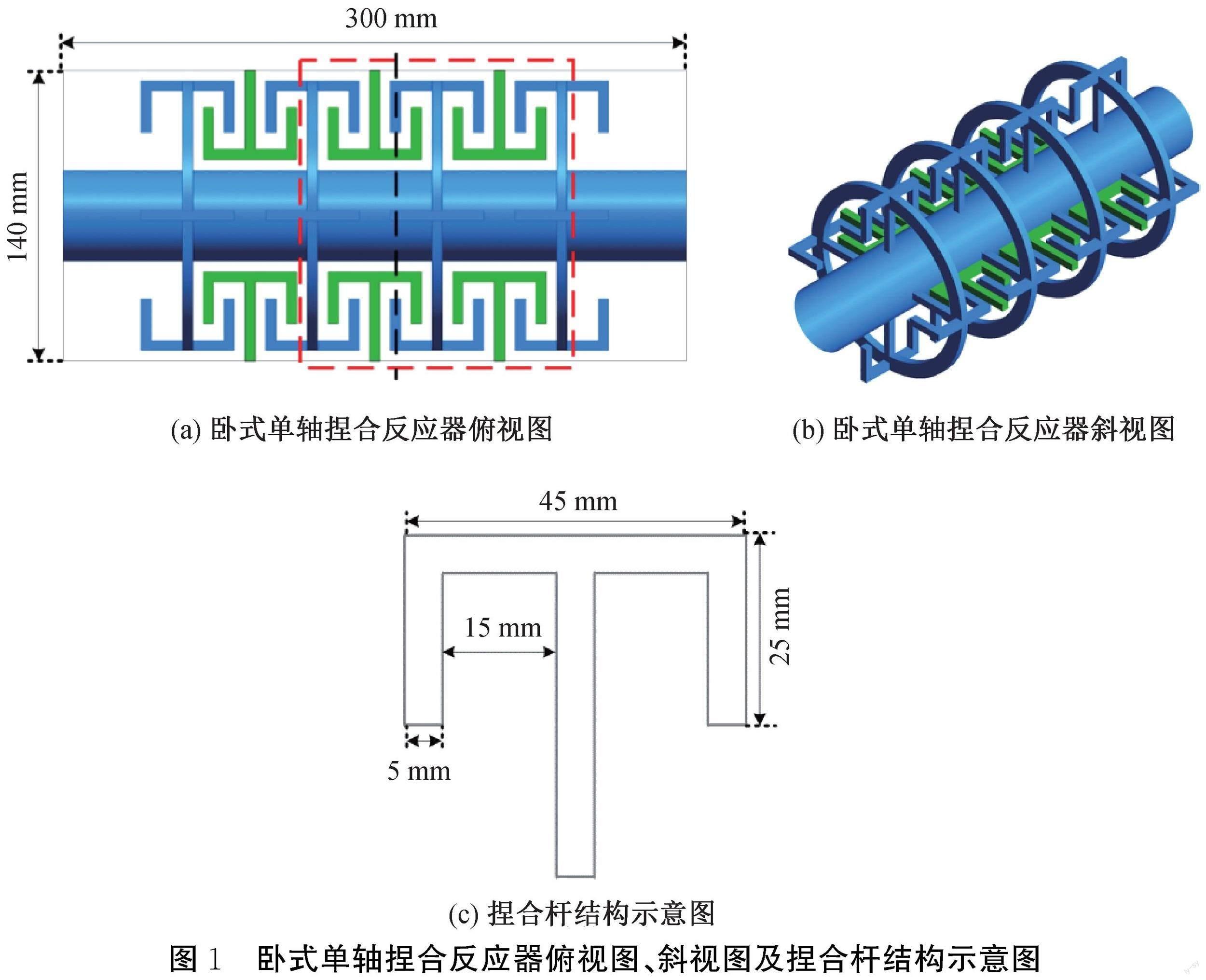
本文的研究对象是一种新型卧式单轴捏合反应器(Single-shaft kneader,SK),其结构示意图如图1所示。反应器半径70 mm,总长300 mm,搅拌轴半径22 mm,桨叶半径65 mm,圆环厚度5 mm,宽度10 mm。捏合杆上侧长度45 mm,侧边长度25 mm。反应器内均匀排列4个搅拌桨叶,每个桨叶由1个圆环和4个动态捏合杆组成,反应器壁面两侧分别等间距设置3个静态捏合杆,静态捏合杆的结构尺寸与桨叶上的动态捏合杆相同。
为了减小计算时长,将计算域限制在图1(a)中红色虚线所围区域,并考虑6种卧式单轴捏合反应器结构,分别记为SK1、SK2、SK3、SK4、SK5和SK6,其结构示意图如图2所示。其中,SK1、SK2、SK3和SK4中的动态捏合杆数目和捏合杆侧边长度相同,静态捏合杆数目分别为0、4、8个和12个;SK2、SK5和SK6的动静态捏合杆数目相同,捏合杆侧边长度分别为25、15 mm和5 mm。具体特征参数见表1。
2 数值模拟及混合特性表征
本文采用计算流体力学软件Polyflow2020R2,使用有限元方法对6种卧式单轴捏合反应器流体流动与混合过程进行模拟,考察不同结构反应器内流体流动与混合特性。
2.1 控制方程
模擬过程中采用广义牛顿流体的Galerkin混合公式,忽略热效应的影响。
连续性方程为:
Δ·v=0(1)
其中:v为流体速度,m/s。
动量守恒方程为:
其中:T为应力张量;p为压力,Pa;ρ为流体密度,kg/m3;t为流动时间,s;f为体积力,N。
通过网格叠加技术处理运动单元的周期性运动。具体地,分别对流道和运动单元进行网格划分,然后按已设定的时间步长将两者的网格叠加[15]。将惩罚项H(v-vp)加入动量守恒方程:
其中:H为从0跳变到1的奇异函数。H=1时,网格点在运动单元内部;H=0时,网格点在运动单元外部。vp是运动单元的速度,m/s。
2.2 计算域网格划分
选取图1(a)中的计算域,使用Gambit 2.4软件分别对流道和运动部件进行六面体网格划分。由于捏合杆末端与壁面间隙较小,流体在此处的速度梯度较大,因此对壁面区域网格进行多层加密。图3(a)为流道网格,图3(b)为运动部件网格,图3(c)为两者叠加网格。选取SK2的网格模型,调整其网格尺寸,划分数目为198970、334244个和529900个的网格模型进行网格无关性验证。选取点(0.022 m, 0.022 m, 0 m)与(0.022 m, 0.022 m, 0.140 m)之间的线段来分析网格数目对速度的影响。不同网格数目下局部速度随轴向距离的变化曲线如图4所示,从图中可以看出:当网格数目大于334244个,速度基本不发生变化。为了兼顾计算时间和准确度,基于SK2中的网格尺寸,划分SK1至SK6的网格数目分别为323084、334244、349004、363764、327844个和321609个。
2.3 模拟策略
模拟物料采用麦芽糖浆,黏度为68 Pa·s,密度为1472 kg/m3。采用Polyflow 2020R2软件并结合有限元方法对卧式单轴捏合反应器内流体的间歇流动和混合过程进行了瞬态模拟,桨叶转速为30 r/min,反应器内速度场的计算采用Mini-element插值,残差设置为10-3。在模拟过程中作以下假设:a)流体流动状態为等温层流流动;b)考虑体积力;c)流体不可压缩;d)流道壁面无滑移。
2.4 混合特性表征
为研究反应器内的流体分布混合过程、拉伸率及混合效率,本文首先采用有限元方法求解流场,然后采用粒子示踪技术分析粒子的运动过程,再通过后处理计算得出分离尺度、平均对数拉伸率及平均时均混合效率。
将粒子随机放置在反应器中;将反应器某一特定区域的粒子浓度设为1,其余区域粒子浓度设为0;当桨叶转动时,不同浓度的粒子之间进行分布混合。为定量分析分布混合过程,本文采用分离尺度Ls进行计算[3],其定义可用式(4)表示:
其中:R(r, t)表示在相同浓度下找到一对相隔一定距离的点的概率,其定义可用式(5)表示:
其中:M为相隔一定距离的点对数目;c′j和c″j为第j对粒子点的浓度;c-为粒子的平均浓度;样本方差σ可用式(6)定义:
相关系数R(r, t)的取值范围为[-1,1]。R为1,表明相隔一定距离的粒子对之间具有相关性(两个粒子浓度相同);R为-1,表明相隔一定距离的粒子对之间不存在相关性(两个粒子浓度相反)[2]。
为研究反应器内的拉伸作用,本文通过动力学方法来跟踪流体单元在运动过程中的局部拉伸变形量[14],进而计算拉伸率λ。在混合初始阶段,流体单元的初始面积为|dX|,一段时间后,流体单元变形后的面积为|dx|,λ可用式(7)表示:
对数拉伸率为:
平均对数拉伸率为:
其中:N为示踪粒子的数目。
瞬时混合效率值eλ为1表示能量耗散用于材料的拉伸,eλ为-1则表示能量耗散用于材料的压缩[16]。eλ可用式(10)表示:
其中:D为应变速率张量。
瞬时混合效率的平均值为:
时均混合效率为:
时均混合效率的平均值为:
为研究反应器的分散混合性能,本文采用混合指数λMZ来反映流场类型对反应器的分散混合性能的影响[16]。λMZ取值范围为[0,1]。当流体流动为纯旋转流时,混合指数为0;为纯剪切流动时,混合指数为0.5;为纯拉伸流动时,混合指数为1。λMZ越接近1,则分散混合性能越好,但同时也应考虑剪切速率的影响。λMZ可用式(14)表示:
其中:Ω为涡量张量。
3 分布混合实验验证
为验证数值模拟的可靠性,搭建了分布混合实验装置,并进行了分布混合实验。分布混合实验装置照片如图5所示,反应器长度和半径分别是300、70 mm,反应器底部到桨叶顶端高度为135 mm。沿搅拌轴等间距放置4个桨叶,每个桨叶上安装4个动态捏合杆,反应器壁面两侧分别等间距安装3个静态捏合杆,动静态捏合杆的结构和尺寸均相同。实验材料为高黏麦芽糖浆(德安府糖业有限公司)和质量分数为2%的羧甲基纤维素钠溶液(上海麦克林生化科技有限公司),其黏度分别为68 Pa·s和58 Pa·s,其密度分别为1472 kg/m3和1012 kg/m3;选取红曲米做示踪剂。实验过程中将桨叶浸没在液体中,模拟设置的物料特性与实验选取的物料特性一致。
利用粒子示踪技术模拟计算粒子的运动过程,并与分布混合实验结果对比,以验证模拟结果的可靠性。糖浆和羧甲基纤维素钠溶液的分布混合实验与数值模拟示意图分别如图6和图7所示。在轴向分布混合实验中,将纯的糖浆、羧甲基纤维素钠溶液以及掺有红曲米的糖浆、羧甲基纤维素钠溶液分别置于反应器的左右两侧区域。在数值模拟中,将红色粒子放在反应器的右侧区域,如图6(a)和图7(a)所示。在径向分布混合实验中,将掺有红曲米的糖浆、羧甲基纤维素钠溶液以及纯的糖浆、羧甲基纤维素钠溶液分别置于反应器的上下两侧区域;在数值模拟中,将红色粒子放在反应器的上侧区域,如图6(b)和图7(b)所示。
从图6和图7中可以看出,分布混合实验结果与数值模拟结果吻合较好。在轴向分布混合实验中,两种颜色流体的界面几乎不发生变化;在数值模拟中,红色粒子基本不向左侧运动,表明没有发生轴向混合,可将捏合杆改装成螺旋结构使其具备轴向推动力。在径向分布混合实验中,桨叶转动带动红色流体运动到下侧区域,两侧不同颜色流体逐渐发生混合,随着桨叶的旋转,更多的红色流体运动到下侧区域;在数值模拟中,随着混合时间的增加,越来越多的红色粒子运动到下侧区域,并分布于整个反应器中,这表明动静态捏合杆间的捏合作用强化了径向分布混合过程。
从整体上看,在两种不同类型流体的径向分布混合实验中,处于上侧区域的红色流体随着混合时间的增加,最终都较为均匀地分布于反应器中,表明卧式单轴捏合反应器能有效强化高黏牛顿流体与非牛顿流体的径向分布混合过程。
4 模拟结果与讨论
本文首先通过有限元方法模拟了不同结构反应器内高黏流体的流动过程,得出反应器结构变化对速度分布、剪切速率分布、混合指数分布的影响规律;然后采用粒子示踪技术对不同结构反应器内高黏流体的混合过程进行分析,得出反应器结构变化对分布混合过程、拉伸率及混合效率的影响规律。
4.1 速度分布
不同结构反应器在Z=0.05 m平面上的速度矢量图如图8所示。从图8中可以看出:物料在桨叶的带动下顺时针转动,动态捏合杆末端的流体速度较高,靠近搅拌轴处的流体速度较小。反应器内并无明显死区,避免了物料因局部滞留而产生热降解[7]。
t=1.0 s时不同结构反应器在Z=0.05 m和Y=0 m平面上的速度分布云图分别如图9和图10所示。从图9和图10中可以看出:高速度区域分布在动态捏合杆末端,搅拌轴及静态捏合杆区域速度较小。随着捏合杆侧边长度的增加,高速度区域的面积随之增大。捏合杆侧边长度的减小导致捏合间隙增大,从而使静态捏合杆附近低速度区域的面积增大。随着静态捏合杆数目增加,高速度区域的面积变化不大,搅拌轴及静态捏合杆附近的低速度區域的面积有所增大。此外,SK2、SK3、SK4、SK5和SK6的动静态捏合杆之间存在相互捏合作用,因此其自清洁效果优于SK1。
4.2 分散混合
t=1.0 s时不同结构反应器在Z=0.05 m和Y=0 m平面上的剪切速率分布云图分别如图11和图12所示。从图11和图12中可以看出:由于捏合杆末端速度较大,高剪切速率区域分布在动态捏合杆末端。此外,高剪切区域的面积随着捏合杆侧边长度和静态捏合杆数目的增加而增大。动静态捏合杆相互捏合时,在反应器内形成间歇区域,速度梯度较大[17],因此SK2、SK3、SK4中高剪切区域的面积大于SK1,更有利于强化分散混合性能。
拉伸流动是比剪切流动更有效的分散混合流动;混合指数越接近1,分散混合性能越好[18]。t=1.0 s时不同结构反应器在Z=0.05 m平面上的混合指数分布云图如图13所示。表2为不同结构反应器在t=1.0 s时混合指数分布大于0.7所占的比例。从图13中可以看出:高混合指数区域出现在相邻动态捏合杆之间,这是由于相邻动态捏合杆之间存在较大的速度梯度,流体在此区域不断地被拉伸和折叠。SK1中的高混合指数区域的面积小于SK2、SK3、SK4,这表明动静态捏合杆间的捏合作用有利于反应器内分散混合性能的提升。高混合指数区域的面积随静态捏合杆数目的增加而先增大后减小。从表2也可看出,反应器内混合指数分布大于0.7所占的比例随静态捏合杆数目的增加而先增大后减小,这表明过多的静态捏合杆降低了反应器内的拉伸流组分。这与Marschik等[19]有关结构对混合器内混合指数的影响类似,该研究发现数目过多的搅拌翅也会导致拉伸流的损失。从混合指数分布云图来看,随着捏合杆侧边长度的增加,对高混合指数区域的面积影响较小;但由表2可以看出,反应器内混合指数分布大于0.7所占的比例随捏合杆侧边长度的增加先增大而减小,这表明捏合杆侧边长度增加能在一定程度上强化反应器的分散混合性能。
4.3 分布混合
为研究反应器内的分布混合过程,在反应器中随机放置5000个粒子,黄蓝粒子各占据反应器内的半部分区域,其中:黄色粒子的浓度为1,蓝色粒子的浓度为0。观察黄蓝粒子的混合过程并计算分离尺度。
SK2的轴向分布混合过程示意图如图14(a)所示,从图中可以看出,黄蓝粒子间的界面基本不随混合时间增加而变化。从轴向与径向分离尺度随时间的变化曲线(图15)可以看出,轴向的分离尺度并没有明显变化。SK2的径向分布混合过程示意图如图14(b)所示,从图中可以看出:在桨叶的带动下,两侧粒子互相交换。t=4.0 s时,反应器内的黄蓝粒子仍存在团聚分层现象。随着混合时间的增加,动静态捏合杆间的捏合作用使粒子的径向分布混合过程得到了强化,两侧粒子的分布逐渐均匀。从图15中可以看出,径向分离尺度在0.0~4.0 s内迅速下降,在9.0 s左右趋于最小值。
不同结构反应器在t=4.0 s时的径向分布混合过程示意图如图16所示,其初始状态与图14(b)初始状态一致。当t=4.0 s时,SK1到SK6的分离尺度分别为0.00840、0.00766、0.00448、0.00335、0.00614 m和0.00532 m。从图16中可以看出:此 时SK1、SK2中的黄蓝粒子仍存在各自团聚、相互分层的现象。随着静态捏合杆数目的增加,分布混合效率得到提升,反应器内黄蓝粒子的均匀化程度更高;随着捏合杆侧边长度的减小,分布混合效率略有提升。
不同结构反应器的径向分离尺度随时间的变化曲线如图17所示。t=2.0 s时,SK1到SK6的分离尺度分别为0.01558、0.01442、0.01091、0.00820、0.01377 m和0.01140 m。t=5.0 s时,SK1到SK6的分离尺度分别为0.00670、0.00522、 0.00349、0.00290、0.00490 m和0.00445 m。不同静态捏合杆数目下反应器的径向分离尺度随时间的变化曲线如图17(a)所示,从图中可以看出:在2.0~5.0 s内,随着静态捏合杆数目的增加,分离尺度下降速率更大,分离尺度更小,分布混合效率更高。这是因为随着静态捏合杆数目增加,捏合频率增大,更容易打破粒子的团聚状态。当混合时间大于16 s时,SK2、SK3、SK4的分离尺度差异不大,但SK1的分离尺度仍处于较高值,这是因为SK1几乎不存在捏合作用,无法对粒子团簇进行有效分散。不同捏合杆侧边长度下反应器的径向分离尺度随时间的变化曲线如图17(b)所示,当捏合杆侧边长度增大时,静态捏合杆占据的空间增大,粒子的运动空间减小,所以从图中可以看出:在2.0~5.0 s内,捏合杆侧边长度的减小使分离尺度下降速率略有增大,总体来看捏合杆侧边长度对分布混合的影响较小。
4.4 拉伸率与混合效率
不同结构反应器的平均对数拉伸率随时间的变化曲线如图18所示。拉伸率随混合时间增加呈指数形式增长,这是有效层流混合的必要条件[14]。混合初始阶段,粒子在动态捏合杆的推动下由静止状态开始运动,更容易被拉伸,所以此时曲线斜率较大,大概3.0 s后,曲线斜率减小并逐渐稳定。当t=60.0 s时,SK1到SK6的平均对数拉伸率分别为7.01、14.40、16.28、16.91、13.83、11.29。不同静态捏合杆数目下反应器的平均对数拉伸率随时间的变化曲线如图18(a)所示,随着静态捏合杆数目的增加,高剪切区域的面积增大,捏合频率增大,粒子所受到的拉伸作用更强,因此从图中可以看出:平均对数拉伸率随着静态捏合杆数目的增加而增大。不同捏合杆侧边长度下反应器的平均对数拉伸率随时间的变化曲线如图18(b)所示,从图中可以看出:平均对数拉伸率随着捏合杆侧边长度的增加而增大。这是因为捏合杆侧边长度增加,高剪切、高速度区域的面积增大,且动静态捏合杆之间的间隙减小,捏合作用增强。
不同结构反应器的平均时均混合效率随时间的变化曲线如图19所示。反应器的平均时均混合效率随混合时间增加一直为正值,表明间歇混合过程中存在较强的重定向作用[14]。粒子由静止开始运动时,平均时均混合效率先迅速提升而后逐渐下降并趋于平稳。不同静态捏合杆数目下反应器的平均时均混合效率随时间的变化曲线如图19(a)所示,从图中可以看出:当混合时间小于30.0 s时,SK1的平均时均混合效率大于SK2、SK3、SK4,这是因为静态捏合杆的存在使反应器内低速区域的面积增加,混合效率降低。动静态捏合杆间的周期性捏合使混合过程得到强化,所以随着混合时间的增加,SK2、SK3、SK4的平均时均混合效率大于SK1。当t=60.0 s时,SK1到SK6的平均时均混合效率分别为0.03503、0.04540、0.04580、0.04366、0.04420,0.04079。随着静态捏合杆数目的增加,高剪切区域的面积增大,捏合频率增大,更容易对粒子团簇进行有效分散,所以平均时均混合效率增大。然而,当静态捏合杆数目过多时,粒子运动空间受限,平均时均混合效率有所下降。不同捏合杆侧边长度下反应器的平均时均混合效率随时间的变化曲线如图19(b)所示,从图中可以看出:平均时均混合效率随着捏合杆侧边长度的增加而增大。这是因为捏合杆侧边长度增加时,高速度、高剪切区域的面积增大,捏合作用增强。
5 结 论
本文采用有限元方法和粒子示踪技术,对高黏流体在不同结构卧式单轴捏合反应器内的流动与混合过程进行了模拟,并通过分布混合实验对数值模拟的可靠性进行了验证,主要得到以下结论:
a)卧式单轴捏合反应器内并无明显死区,动静态捏合杆间的捏合作用使反应器具有一定的自清洁效果。高速度、高剪切区域分布于动态捏合杆末端,且高速度、高剪切区域的面积随着捏合杆侧边长度的增加而增大,静态捏合杆数目的增加会增大高剪切区域的面积及搅拌轴附近的低速区域的面积。
b)相邻动态捏合杆之间存在较大的速度梯度,流体在此区域不断地被拉伸和折叠,因此在此区域内高混合指数区域的面积分布较大。动静态捏合杆间的捏合作用增强了分散混合性能。随着静态捏合杆数目和捏合杆侧边长度的增加,反应器内混合指数分布大于0.7所占的比例先增大后减小;过多增加静态捏合杆数目和捏合杆侧边长度将使拉伸流组分损失,不利于分散混合性能的提升。
c)动静态捏合杆间的捏合作用有效强化了径向分布混合过程。捏合杆侧边长度对分布混合影响较小;随着静态捏合杆数目的增加,捏合频率增大,更容易打破粒子团聚状态,从而强化了分布混合过程,分离尺度随之减小。
d)拉伸率随混合时间增加呈现指数形式增加,平均时均混合效率随混合时间增加一直为正值。平均对数拉伸率随着静态捏合杆数目和捏合杆侧边长度的增加而增大;静态捏合杆数目和捏合杆侧边长度的增加都使平均时均混合效率得到提升,但当静态捏合杆数目过多时,混合效率呈现下降趋势。
本文研究了反应器结构变化对卧式单轴捏合反应器内流体流动与混合特性的影响规律,对卧式单轴捏合反应器的优化设计具有理论指导意义。
参考文献:
[1]Cheng W K, Wang J J, Gu X P, et al. Film formation and mass transfer characteristics in a horizontal self-cleaning twin-shaft kneader with highly viscous Newtonian fluids[J]. Industrial & Engineering Chemistry Research, 2021, 60(3): 1405-1411.
[2]成文凯, 张先明, 王嘉骏, 等. 反向旋转卧式双轴捏合反应器混合特性的数值模拟[J]. 化工学报, 2022, 73(1): 162-174.
[3]Cheng W K, Ye Y, Jiang S X, et al. Mixing intensification in a horizontal self-cleaning twin-shaft kneader with a highly viscous Newtonian fluid[J]. Chemical Engineering Science, 2019, 201: 437-447.
[4]成文凯. 卧式双轴搅拌脱挥设备的成膜特性与传质过程强化[D]. 杭州: 浙江大学, 2019: 9-10.
[5]焦海亮, 包雨云, 黄雄斌, 等. 高黏度流体混合研究进展[J]. 化工进展, 2007, 26(11): 1574-1582.
[6]马青山, 冯连芳, 顾雪萍, 等. 卧式单轴粉体搅拌反应器的搅拌功率[J]. 高校化学工程学报, 1999, 13(1): 31-37.
[7]Fleury P A. Bulk polymerisation or copolymerisation in a novel continuous kneader reactor[J]. Macromolecular Symposia, 2006, 243(1): 287-298.
[8]成文凯, 王嘉駿, 顾雪萍, 等. 聚合物搅拌脱挥设备及其 CFD 模拟研究进展[J]. 化工进展. 2016, 35(5): 1283-1288.
[9]王嘉骏, 顾雪萍, 冯连芳, 等. 卧式搅拌槽内流体混合的实验与模拟研究[J]. 中国科技论文在线, 2008, 3(12): 911-914.
[10]罗彬彬. 卧式单轴自清洁搅拌釜气液分层流和传热过程数值研究[D]. 天津: 天津大学, 2017: 36-50.
[11]单纯. 卧式单轴自清洁搅拌釜数值模拟[D]. 天津: 天津大学, 2013: 42-56.
[12]韩海川, 刘谨, 李开国, 等. 双螺杆啮合元件与反螺纹元件对流场影响的仿真[J]. 工程塑料应用, 2020, 48(6): 74-77.
[13]刘杨, 朱向哲. 新型偏心三螺杆挤出机流体混合特性分析[J]. 中国塑料, 2022, 36(7): 150-156.
[14]Cheng W K, Xin S C, Chen S C, et al. Hydrodynamics and mixing process in a horizontal self-cleaning opposite-rotating twin-shaft kneader[J]. Chemical Engineering Science, 2021, 241: 116700.
[15]Xin S C, Cheng W K, Yang L S, et al. Hydrodynamics and mixing performance in a continuous miniature conical counter-rotating twin-screw extruder[J]. International Journal of Chemical Reactor Engineering, 2022, 20(11): 1117-1130.
[16]辛思成, 成文凱, 张先明. 反向旋转微型锥形双螺杆挤出机混合性能的数值模拟[J]. 浙江理工大学学报(自然科学版), 2021, 45(4): 527-533.
[17]成文凯, 张先明, 王嘉骏, 等. 卧式单轴捏合反应器流动与混合特性的数值模拟[J]. 化工学报, 2022, 73(5): 1995-2007.
[18]Pandey V, Maia J M. Comparative computational analysis of dispersive mixing in extension-dominated mixers for single-screw extruders[J]. Polymer Engineering & Science, 2020, 60(10): 2390-2402.
[19]Marschik C, Osswald T A, Roland W, et al. Numerical analysis of mixing in block-head mixing screws[J]. Polymer Engineering & Science, 2019, 59(s2): E88-E104.
