基于多视角图像三维重建与点云配准的着装间隙量表征

卢志洁 侯珏 杨阳 刘正

摘 要： 为了分析人体不同姿势下的着装间隙量，采用多视角图像三维重建方法获取净体和着装的三维点云，利用OpenPose人体姿态估计模型确定关节点并逆投影到三维空间，获得净体和着装两层点云粗配准的匹配点坐标；基于着装未覆盖的人体点云，通过最近点迭代（Iterative closest point，ICP）算法实现两层点云的精配准，并对配准模型进行验证，建立三维着装模型。根据三维着装模型计算两层点云间的最近邻域距离表征着装间隙量。结果显示：经两步配准后，躯干着装未覆盖处两层点云距离平均值和均方根误差分别为2.859 mm和3.260 mm，胳膊区域两层点云距离最大的平均值和均方根误差分别为4.018 mm和4.735 mm，配准结果精准度较好。该方法可以准确地获取不同姿势的着装间隙量的大小与分布，为分析着装间隙量与运动的关系、评价舒适性、建立热传递模型及评估虚拟试衣效果提供关键技术手段。

关键词： 着装间隙量；三维重建；点云配准；三维着装模型；多视角图像

中图分类号： TS941.2

文献标志码： A

文章编号： 1673-3851 （2024） 03-0202-08

Characterization of clothing ease allowance based on the 3D reconstruction and point cloud registration of multi-view images

Abstract：  To analyze the amount of clothing ease allowance under different postures of the human body， the three-dimensional （3D） point cloud of the nude body and clothing was obtained by 3D reconstruction based on multi-view images. Using the human pose estimation model of OpenPose， we estimated the joints and reversely projected them to the 3D space to get the coordinates of the matching points for the coarse registration of the two layers of point clouds of the nude body and clothing. We realized the accurate registration of the two layers of point clouds based on the uncovered human body point clouds by the iterative closest point （ICP） algorithm， and verified the registration model， building a 3D dressing model. Based on the model， we computed the nearest-neighbor distance between the two layers of point clouds， and defined the distance as the ease allowance. The results showed that after two-step registration， the average distance and root mean square error of the two layers of point clouds in the uncovered area of the torso were 2.859 mm and 3.260 mm， respectively， and the maximum average distance and root mean square error of the two layers of point clouds in the arm area were 4.018 mm and 4.735 mm， respectively， indicating good accuracy in registration results. This method can accurately obtain the size and distribution of clothing ease allowance for different postures and provide key technical means for analyzing the relationship between clothing ease allowance and movement， evaluating comfort， establishing heat transfer models， and evaluating virtual fitting effects.

Key words： clothing ease allowance; 3D reconstruction; point cloud registration; 3D dressing model; multi-view images

0 引 言

著装间隙量是着装状态下人皮肤表面与服装内表面之间的空隙宽度［1］，在评估服装合体性［2］、建立人-服装-环境系统的热传递模型［3-4］以及衡量三维虚拟试衣效果［5］等方面都有广泛应用。目前，获取着装间隙量的主要方法是三维扫描测量，该方法测量的着装间隙量精度取决于三维扫描数据质量和点云的配准。将净体和着装两层点云按照真实穿着状态对齐，即点云配准，得到三维着装模型。若配准不佳，将导致衣下空间的位置偏移和形态改变，从而产生误差。现有三维扫描仪的精度能满足计算着装间隙量的要求，因此配准的精度是确保准确获得着装间隙量分布和形态的关键。目前，研究人员主要利用扫描假人获取间隙量，进而研究面料、松量及款式等因素对于着装间隙量的影响［6-7］，然而针对真人在不同姿态下的配准研究较少。对于动态着装间隙量的获取，需采用若干个离散的人体姿势呈现运动状态［8］，然而假人无法体现人体运动过程中肌肉、皮肤等体表形态的变化，若采用真人扫描实验，人体位置变化和姿势不稳定给点云配准带来了极大的挑战。

随着计算机视觉技术发展，基于图像的三维人体重建成为研究的热点。潘博等［9］基于多视角图像利用三维重建获取服装的点云数据并进行优化，得到表面细节清晰的服装点云模型，可用于服装虚拟展示；Zhao等［10］基于多视角图像分别重建人体稀疏点云和人体稠密点云，并获得了人体的围度数据；Zhu等［11］通过基于视频重建人体稠密点云，提出了使用点云增强来检测和调整冲突点数据，生成的人体模型可用于3D打印。现有的三维人体重建研究多集中于单个人体或服装模型，鲜有通过配准净体和着装点云来模拟真实的穿衣状态，探究衣下空间形态。

为高效获取点云，解决基于真人建立三维着装模型中的点云配准的问题，并准确表征着装间隙量，本文提出了一种基于多视角图像三维重建净体和着装点云，配准两层点云模拟真实穿着状态，进而表征着装间隙量的方法。为了减少人对服装的遮挡，以常见的抬臂运动［12］为例，用4个离散的抬臂姿势代替抬臂运动，分别拍摄净体和着装的多视角图像，利用三维重建获得净体和着装点云；通过粗配准和精配准净体和着装两层点云，构建配准模型，通过客观指标验证配准的精准度；去除着装点云未被服装覆盖区域的点云，获得三维着装模型；计算两层点云之间的最近邻域距离，表征抬臂运动中着装间隙量，可为分析着装间隙量提供了一种快速可行的方法。

1 人体与服装的三维重建实验

1.1 图像采集

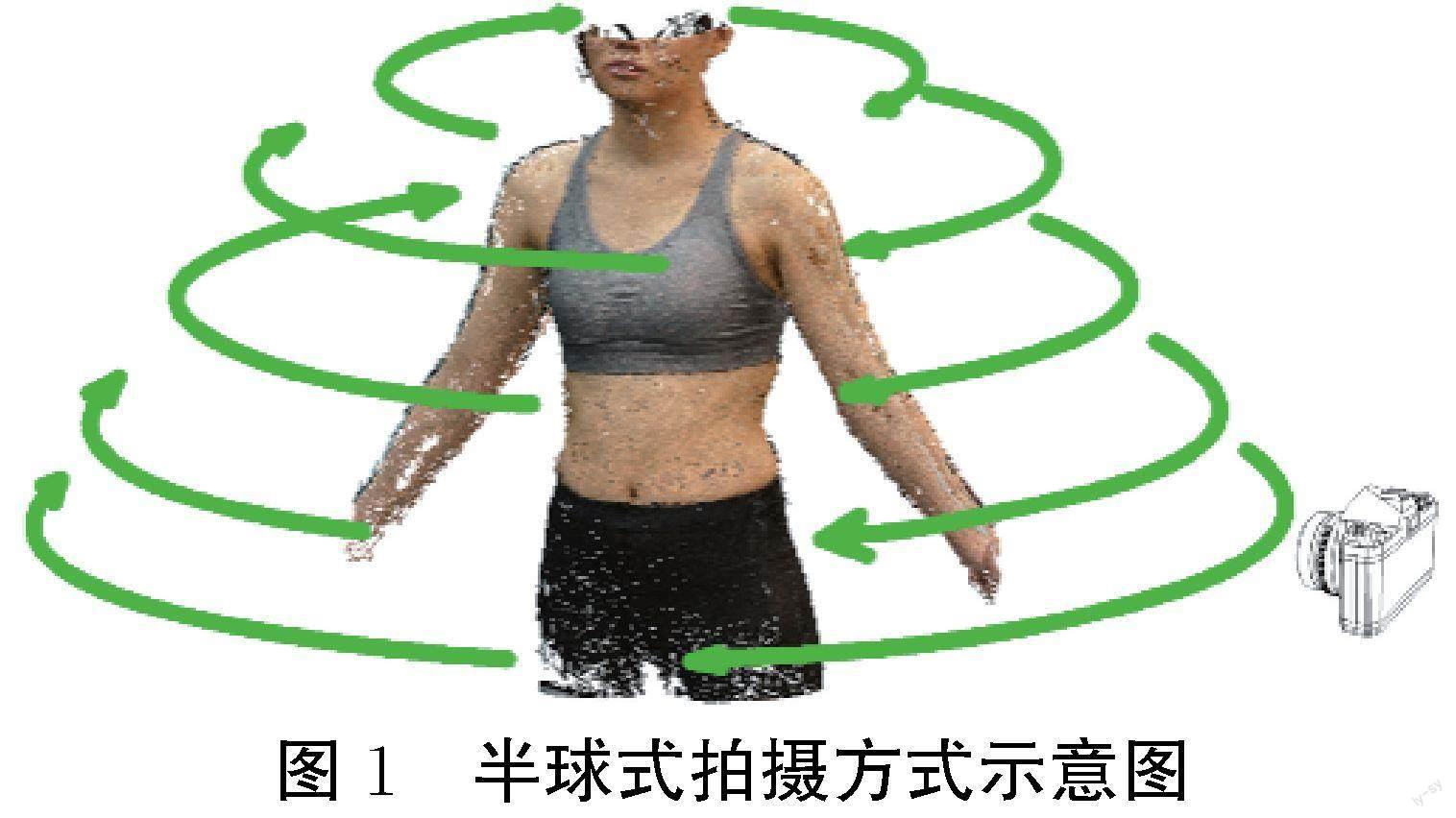
测试对象身高为162 cm、胸围为82 cm、腰围为66 cm，测试服装为白色无图案宽松背心，衣长为60 cm，胸围为106 cm，腰围为92 cm，肩宽为40 cm。分别拍摄测试对象在侧向抬臂45°、90°、135°和180°动作下的净体和着装图像。本文采用半球式拍摄方式采集图像，如图1所示：手持相机以不同半径和高度围绕测试对象拍摄，使用相机支架增加稳定性和保持每一圈拍摄高度相同，拍摄距离由远及近，拍摄高度由下及上；在同一高度拍摄的相邻两张图片之间的角度不超过20°，保证有70%以上的重叠区域，每次拍摄保证采集到100张以上图像。

1.2 点云数据计算

三维重建点云流程主要包括两个过程：基于运动中恢复场景结构（Structure from motion，SFM）算法重建稀疏点云，通过多视角立体视觉（Multi-view stereo，MVS）算法重建稠密点云［13］。通过SFM算法，根据图像特征点对多视角图像序列进行匹配并验证，利用对极几何和三角测量方法重建出三维场景的稀疏点云和求解相机参数［14］。稀疏重建   通常是重建图像特征点的三维坐标，对于计算着装间隙量来说，点云的数量过少，需要进一步进行稠密重建。MVS算法的输入为一组图像和相应的相机参数，输出为稠密点云。该算法通过构造与累积匹配代价完成匹配图像对应点，计算点的深度值得到每张图像的深度图并优化，最后将多视角图像的深度图融合得到三维点云［15］。本文基于SFM算法和MVS算法计算净体和着装的点云数据流程如图2所示。

2 点云数据处理

2.1 点云数据预处理

三维重建场景与世界坐标系不平行，为了方便后续处理，基于地面绝对水平的原则，利用侧视图和前视图场景中的地板与世界坐标系轴的夹角，将场景旋转至与世界坐标系平行。稠密点云的方向规格化示意图见图3，其中通过三维重建获得的稠密点云如图3（a）所示，旋转后的场景如图3（b）所示。

SFM算法在求解相机参数时未能保留真实的物理尺寸，导致重建的三维点云数据与真实值存在一个尺度因子S的差异。为了将点云恢复成真实的物理尺寸，测量场景点云中物体的大小，计算真实物体尺寸与测量值的比值并对点云进行尺度变换。本文将地板作为参照物将点云恢复成真实物理尺寸，设重建场景中地板的尺寸为L1，真实尺寸为L2，则S=L2/L1，所有点放大S倍得到与真实尺寸一致的点云。

在完成尺度变换后，对背景点云进行剔除，得到穿着紧身衣和穿着测试服装人体的稠密点云，分别称为净体点云B和着装点云G，如图4所示。

2.2 点云配准

2.2.1 基于关节点的点云粗配准

粗配准需要在两个待配准的点云中选择匹配点对，在着装和不同姿态的情况下很难在人体表面选择能够用于匹配的特征点，但在抬臂过程中位于人体躯干上的髋关节点和颈关节点的位置基本不会发生改变。因此，本文选择髋关节点和颈关节点作为粗配准的匹配点，其三维坐标可通过逆投影关节点的像素坐标计算得到。

OpenPose是实时检测单张图像上人体面部、四肢、躯干的人体姿态估计模型［16］，本文利用OpenPose模型获得图像中的颈关节点和左右髋关节点的像素坐标，在已知像素坐标和相机参数的前提下，可根据相机投影原理计算关节点的三维坐标，该过程本质上是将二维平面上的离散点重新投影到三维空间中，其基本数学模型：

其中：u、v为图像上点的像素坐标，zc为相机坐标系下点的深度方向的坐标，ax、ay为相机的像素焦距，u0、v0为主点坐标；R是旋转矩阵，是平移向量，K为相机的内参矩阵，E为相机的外参矩阵，可以通过1.2节所述的SFM算法得到；合并K和E得到向量mT1，mT2和mT3，W=（xw，yw，zw）是点的齐次世界坐标。

式（1）描述的为理想相机成像模型，但是实际情况中的图像畸变会导致点的位置发生失真问题，为了获取真实的关节点的像素坐标，需要对图像做去畸变处理。畸变分为径向畸變和切向畸变，由径向畸变系数k1、k2、k3和切向畸变系数p1、p2表示，通常径向畸变较大，本文仅考虑对径向畸变影响最大的系数k1。设点在相机坐标系中畸变后的坐标C=（xc_d， yc_d， zc_d）T，理想的坐标Cc_i=（xc_i， yc_i， zc_i）T，则畸变模型可以表示为：

根据相机成像模型求解关节点的三维坐标，以左髋关节点为例，设图像A和图像B的左髋关节点的像素坐标（uA_d，vA_d）和（uB_d，vB_d），三维坐标WL=（xw_l， yw_l， zw_l）；将像素坐标转换成相机坐标系下的坐标，根据式（2）去畸变得到无畸变的相机坐标，再将其转换为像素坐标（uA，vA）和（uB，vB），分别代入式（1），化简得：

合并式（3）和式（4）得：

式（5）是超正定方程，需将超正定方程转化为一个带约束的最小二乘问题求解。将式（5）简写为Mw=0，求解向量w，使得w=argmin‖Mw‖2，s.t.‖w2‖=1。通过拉格朗日乘数法得：

MTMw=λw（6）

其中：λ和w分别是MTM的特征值和特征向量，且‖Mw‖2=wTMTMw，即当λ取最小值时，求得式（5）的最小二乘解。将关节点与三维重建的点云合并，并放大到真实尺寸，将其作为匹配点对点云B和G进行粗配准。

2.2.2 基于ICP算法的点云精配准

经过ICP算法计算得到变换后的着装点云G′。去除着装点云G′未被服装遮盖的胳膊、颈部等部位的点云，得到三维着装模型，用于计算着装间隙量。

2.3 着装间隙量表征

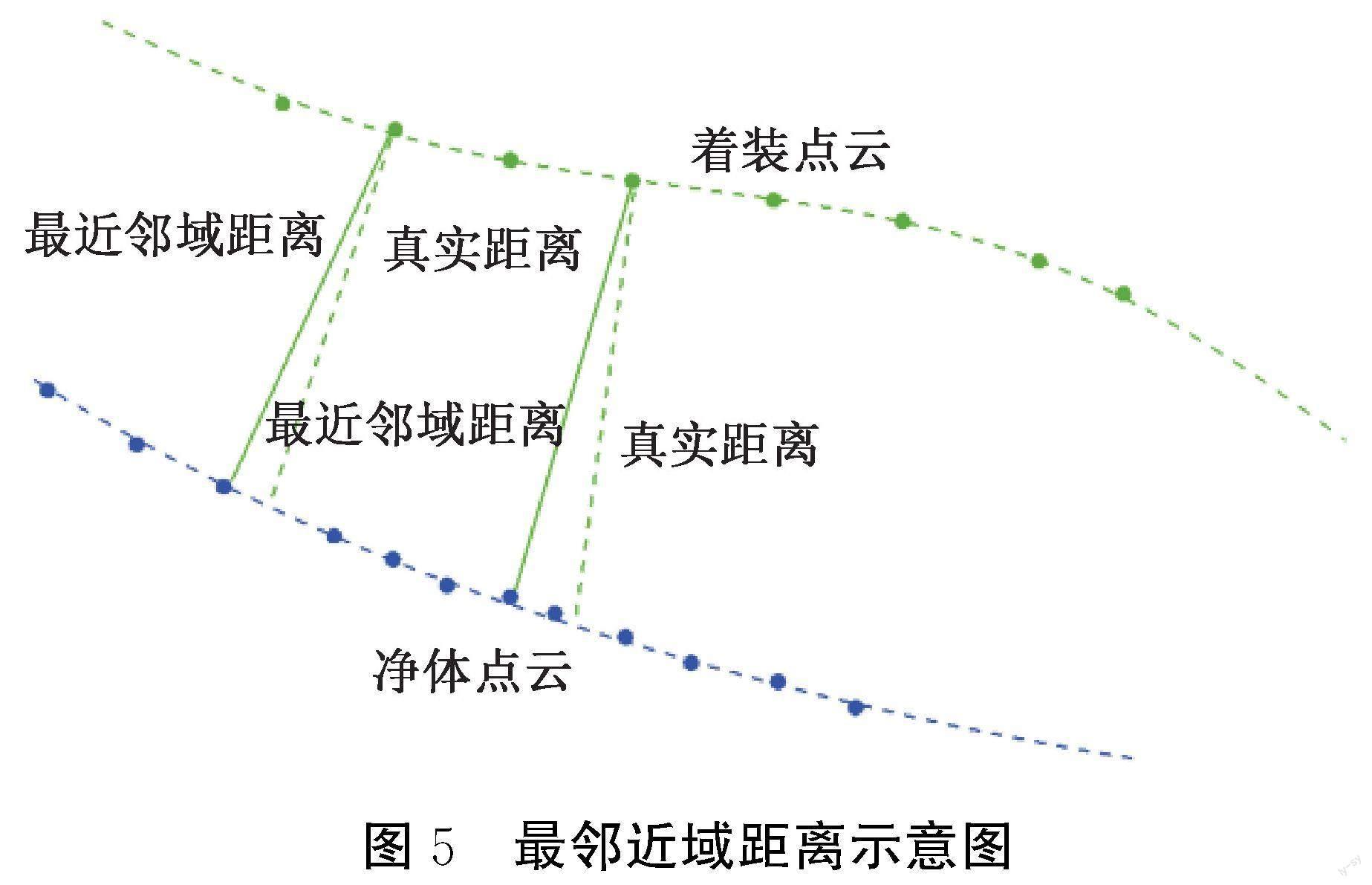
着装间隙量一般采用服装和人体之间的距离作为表征方式。通过三维扫描获得的点云数据比较稀疏，需要对点云进行封装处理，得到网格模型，然后利用逆向工程软件计算网格模型之间的距离作为着装间隙量。而通过三维重建获得的点云数据点云密度较大，两个点云之间的最近邻域距离与真实距离（即法线距离）相差较小，本文将三维着装模型中净体点云与服装点云之间的最近邻域距离定义为着装间隙量，如图5所示。

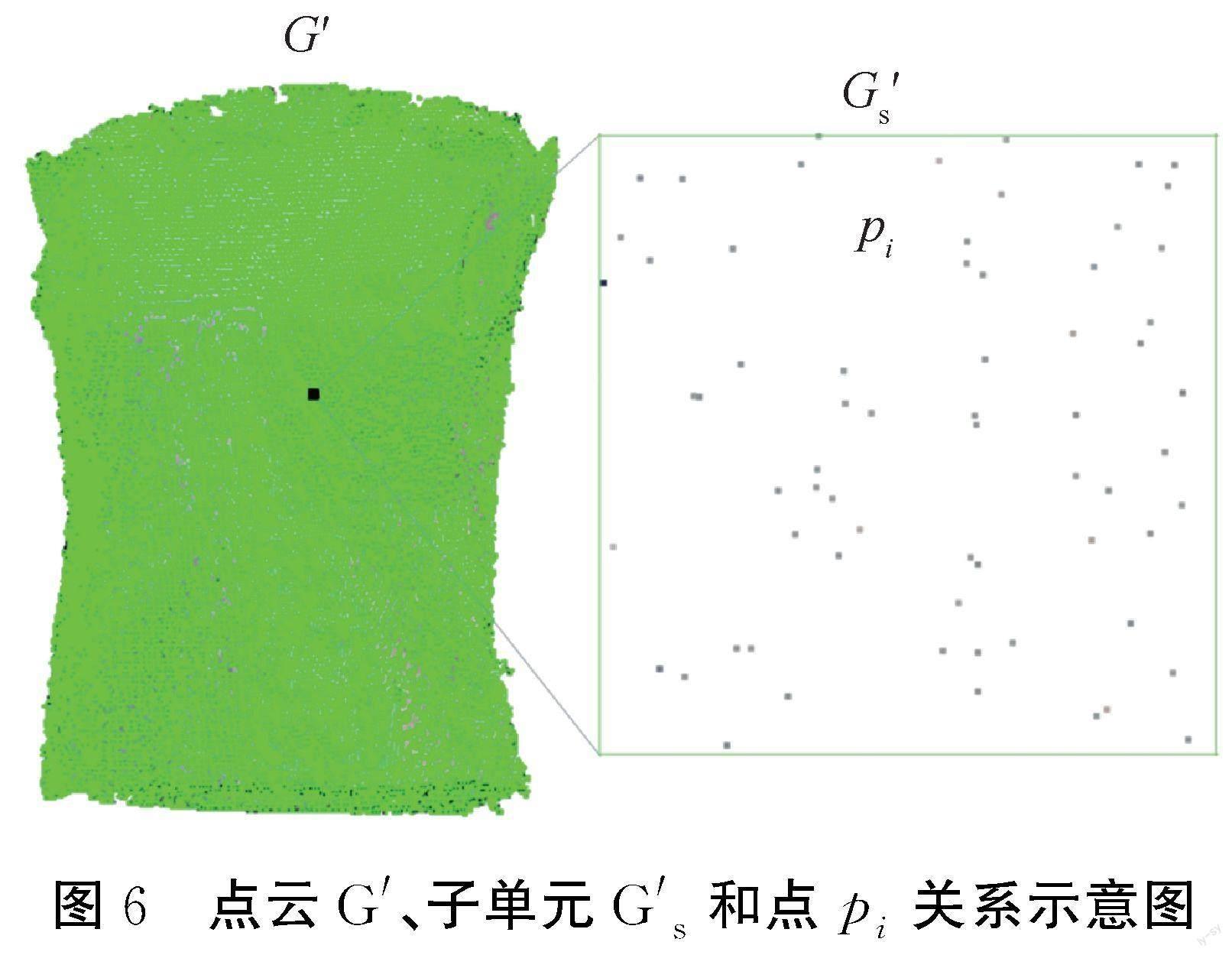
为计算点云B和G′之间的最近邻域距离，通过八叉树将点云B和G′划分为8个子立方体，并在每个子立方体递归地继续构建子八叉树，当达到给定细分水平时停止划分。这种结构可以快速查找特定点的子单元位置及其邻域单元，提高计算速度。设G′s是点云G′在给定细分水平上子单元中的一个子集，包含若干个点pi，三者关系如图6所示。Bs是G′s最邻近单元的点云B的子集，为找到真正的最近点，对于G′s中每一个点，计算其到所有最邻近单元Bs中包含的所有点的欧氏距离，直到最小距离小于以点pi为球心，并且完全包含该邻域单元球体的半径，定义此距离为最近邻域距离［17］。即对于着装点云中的每一个点，搜索净体点云中最近的点并且计算两个点之间的欧式距离，所得到的距离值即为着装间隙量。

3 结果与分析

3.1 配准结果及误差分析

表1是净体和着装状态下关节点的三维坐标，在三维空间中的位置如图7所示。图8展示了净体和着装点云相对位置在粗配准前后的对比。通过三维图像可以看出，在粗配准后两个点云的相对位置存在误差，但可以为精配准提供较好的初值。

理想情况下，左右髋关节点y坐标和z坐标应基本在同一水平线上，但左右髋关节y和z坐标的最大差异为23.008 mm；颈关节点x坐标应位于左右髋关节中心，但最大差异为29.299 mm。通过逆投影得到的关节点坐标，产生误差是多方面导致的：SFM算法求解相机的参数与真实的参数之间存在一定的误差；求解超正定方程的结果是最小二乘解；OpenPose模型将关节简化为一个点，导致两张图像上估计的关节点指的并不是空间中的同一个三维点。

在稀疏重建的过程中已经基于尺度不变特征转换（Scale-invariant feature transform，SIFT）算法提取了图像中特征点的像素坐标，本文通过对比特征点与关节点的三维坐标误差，分析误差产生的主要原因。分别利用SFM算法和基于逆投影计算得到特征点的三维坐标并对比，结果如表2所示，3个方向的坐标差证明了相机参数和求解方程存在误差，最大误差为4.320 mm，远小于关节点的误差，说明OpenPose模型估计的关节点并不完全匹配是导致误差的主要原因。

经过ICP算法得到的精配准结果如图9所示，从三维图像中可以看出，服装在肩部有些穿透，这是因为肩部服装紧贴人体，而且两次拍摄时姿势存在细微的差异，但从整体来看两个点云基本配准，得到基本符合真实穿着状态的三维着装模型。

3.2 配准结果验证

点云的配准结果可以通过主观视觉检查和客观指标的方法进行评价。使用点云可视化软件或处理点云的库加载配准后的点云，观察点云的配准情况，检查是否存在明显的偏移或未对齐的区域。将点对之间的距离作为指标来衡量配准质量，常见的方法是计算点到最近邻点的欧氏距离，并计算其平均值（D-）或均方根误差（RMSE）［18］，较小的误差值表示配准结果较好。图9为经两步配准的结果，视觉上两个点云在共同区域如颈部和左右胳膊区域重合，为进一步验证配准结果，本文通过点云B和G′共同区域的点云之间距离的平均值和均方根误差衡量两个点云之间空间位置的差异，平均值和均方根误差计算公式分别为：

其中：di （i=1， 2，…，N）是同一区域两层点云之间的最近邻域距离，N为点云的个数。

分割点云B和G′左胳膊、右胳膊和颈部的点云，分别计算3个区域点云之间距离的平均值和均方根误差，计算结果如表3所示。

计算结果证明配准后人体和服装空间相对位置接近真实情况。而右胳膊点云之间RMSE的和D-偏大有两个原因：一方面，观察点云三维图像可发现右胳膊上方点云稀疏，得到的点云最近邻域距离偏大；另一方面，两次姿势的差异同样会导致结果偏大。

3.3 着装间隙量计算结果与分析

根据2.3计算不同抬臂角度三维着装模型中净体和着装点云的最近邻域距离，得到着装间隙量大小与分布结果如图10所示。分析三维图像可得：在运动过程中，人体的凹凸形态、服装变形和人体尺寸随运动发生变化是影响着装间隙量变化的主要因素。

人体的凹凸形态是影响标准站姿下着装间隙量分布的重要因素之一，在运动过程中也一定程度影响着装间隙量的分布。抬臂45°时，着装间隙量的分布主要受人体的凹凸形态影响，如图10（a）所示。腰部后面和侧面区域的着装间隙量较大。在抬臂过程中，肩部、胸高点周围、臀部等凸区域服装贴体，着装间隙量始终处于0～6 mm，这与Zhang等［19］研究结果一致。人体运动产生的服装变形对着装间隙量的大小和分布具有显著影响。随着抬臂角度的增大服裝在不同区域变形不同，整体上腰腹部的空气逐渐向胸背部转移，背部区域着装间隙量明显增加，如图10（c）—（d）所示。抬臂90°时，服装较平整，随着抬臂角度增大，前胸和后背处形成大量U形褶皱，在褶皱凸起部位的着装间隙量增大，由于人体后腰凹陷处于“U”的底部，后腰区域着装间隙量下降幅度相对较大，由最远离人体到逐渐贴合人体，同时肩胛骨处的着装间隙量逐渐增大至40 mm左右；远离肩部的服装区域向左右两侧位移，前后的空气逐渐向两侧转移，导致在人体前中和后中附近区域着装间隙量减小，而在左右两侧区域着装间隙量增大。运动过程中变化的人体尺寸的变化对着装间隙量有一定程度的影响。抬臂会使得人体躯干不自觉向前倾，人体前后的曲线发生变化，腰腹部肌肉和皮肤收紧，使人体前面更加贴合服装，从图10中可以看出，胸部以下的着装间隙量整体变小。

4 结 论

本文提出了一种基于多视角图像三维重建着装和净体点云，配准两层点云模拟真实穿着状态，进而获取着装间隙量的方法。利用SFM算法和MVS算法得到不同姿势下人体和服装的稠密点云，高效获取点云数据；基于关节点将净体和着装点云进行粗配准，基于着装未覆盖区域点云利用ICP算法对两层点云进行精配准，为准确表征间隙量提供了必要条件；采用点云之间最近邻域距离表征间隙量，缩短计算间隙量的流程。配准结果显示，躯干着装未覆盖处两层点云距离平均值和均方根误差分别为2.859 mm和3.260 mm，胳膊区域两层点云距离最大的平均值和均方根误差分别为4.018 mm和4.735 mm，表明着装模型基本接近真实状态，能准确表征间隙量。目前求解得到的关节点三维坐标存在误差，后续可以采用三维关节点检测技术直接获得关节点三维的坐标从而减小误差，以提高配准的效率与准确性。

参考文献：

［1］刘正，李基拓，陆国栋，等. 着装间隙量空间形态分布研究及其应用综述［J］. 计算机辅助设计与图形学学报，2012，24（10）：1294-1301.

［2］王诗潭，汪秀花，王云仪. 连体服衣下间隙特征指标的确定及其在服装合体性评价中的应用［J］. 纺织学报，2021，42（9）：137-143.

［3］Li J， Zhang Z H， Wang Y Y. The relationship between air gap sizes and clothing heat transfer performance［J］. The Journal of the Textile Institute， 2013， 104（12）： 1327-1336.

［4］姜茸凡，王云仪.服装衣下空气层热传递性能研究进展［J］.絲绸，2018，55（7）：41-48.

［5］Lage· A， Ancutiene· K， Pukiene· R， et al. Comparative study of real and virtual garments appearance and distance ease［J］. Materials Science， 2020， 26（2）： 233-239.

［6］Lu Y， Song G， Li J. A novel approach for fit analysis of thermal protective clothing using three-dimensional body scanning［J］. Applied ergonomics， 2014， 45（6）： 1439-1446.

［7］王云仪，张雪，李小辉，等. 基于Geomagic软件的燃烧假人衣下空气层特征提取［J］. 纺织学报，2012，33（11）：102-106.

［8］Wang S T， Wang X H， Wang Y Y. Effects of clothing ease and body postures on the air gap and clothing coverage［J］. International Journal of Clothing Science and Technology， 2019， 31（4）： 578-594.

［9］潘博，钟跃崎. 基于二维图像的三维服装重建［J］. 纺织学报，2020，41（4）：123-128.

［10］Zhao Y， Mo Y， Sun M Q， et al. Comparison of three-dimensional reconstruction approaches for anthropometry in apparel design［J］. The Journal of The Textile Institute， 2019， 110（11）： 1635-1643.

［11］Zhu H， Liu Y B， Fan J T， et al. Video-based outdoor human reconstruction［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2017， 27（4）： 760-770.

［12］倪军，张昭华，王文玲，等.衣袖结构设计对上肢运动灵活性的影响［J］.东华大学学报（自然科学版），2020，46（1）：41-46.

［13］zye瘙塂il O， Voroninski V， Basri R， et al. A survey of structure from motion［J］. Acta Numerica， 2017， 26： 305-364.

［14］Schnberger J L， Frahm J M. Structure-from-motion revisited［C］∥IEEE/CVF Conference on Computer Vision and Pattern Recognition（CVPR）. Las Vegas， NV，US：IEEE，2016： 4104-4113.

［15］Schnberger J L， Zheng E， Frahm J M， et al. Pixelwise view selection for unstructured multi-view stereo［C］∥ 14th European Conference on Computer Vision（ECCV）. Lecture Notes in Computer Science. Amsterdam， Netherlands： Springer， Cham， 2016： 501-518.

［16］Cao Z， Simon T， Wei S E， et al. Realtime multi-person 2D pose estimation using part affinity fields［C］∥ IEEE/CVF Conference on Computer Vision and Pattern Recognition（CVPR）. Honolulu， HI， USA：IEEE，2017： 7291-7299.

［17］Girardeau-Montaut D， Roux M， Marc R， et al. Change detection on points cloud data acquired with a ground laser scanner［J］. International Archives of Photogrammetry， Remote Sensing and Spatial Information Sciences， 2005， 36（3）： W19.

［18］Hui F， Zhu J Y， Hu P C， et al. Image-based dynamic quantification and high-accuracy 3D evaluation of canopy structure of plant populations［J］. Annals of Botany， 2018， 121（5）： 1079-1088.

［19］Zhang Z H， Ni J， Zhou Y. The effect of arm postures and garment style on local mobility and thermal insulation［J］. AATCC Journal of Research， 2022， 9（1）： 12-22.