光伏光热墙体结构优化模拟研究
2024-04-03李佳琪蔡庆峰王晓梦王泽林
李佳琪, 刘 芳, 蔡庆峰, 王晓梦, 王泽林
(山东建筑大学热能工程学院,山东济南250101)
1 概述
随着经济发展和城市建设不断推进,化石能源消耗持续增加。在全球范围内,建筑能耗约占能耗总量的40%左右。为减少建筑能耗,众多学者对太阳能利用进行了广泛研究。太阳能空气集热器是太阳能利用的主要装置之一,太阳能光伏光热系统能够将接收的太阳能同时转化为电和热[1-3]。
特朗伯墙是一种依靠墙体独特的构造设计,无机械动力、无传统能源消耗,仅依靠被动式收集太阳能为建筑供暖的集热墙体。特朗伯墙由法国太阳能实验室主任Trombe教授及其合作者首先提出并实验成功,因此称为Trombewall(特朗伯墙)。众多学者基于特朗伯墙原理进行了实验和模拟研究。Peng等人[4-5]研究了不同通风模式下的通风光伏立面墙的电热性能,并针对不同天气条件提出了适当的运行策略。实验结果表明,通风模式可降低光伏组件的工作温度,从而提高系统的发电效率。虞丽丹[6]对光伏光热墙体系统流道内空气流动的传热特性进行分析,结果表明,可以在允许的范围内尽量增加流道的高度,但流道的宽度一般不宜大于70 mm;当高宽比大于30时,更有利于流道内的流动传热。Alberto等人[7]认为对双层幕墙效率影响最大的是气流路径,双层立面结构能够最大限度降低气隙内部空气温度。Preet等人[8]发现合理的空气流道和风速组合可显著提高光伏系统的电功率输出。Zhu等人[9]提出了一种设置双层相变材料板的特朗伯墙,结果表明,相变材料板可改善建筑围护结构的全年热性能。Ling等人[10]和Meng等人[11]证明了相变材料能够降低建筑能耗、提高用能效率。Preet等人[12]分析指出,将相变材料与光伏光热系统结合可提高发电效率和热效率。
研究表明,光伏板温度上升1 ℃,光电转换效率下降0.3%~0.5%。而风道与光伏板的结合既有利于光伏板降温,也可以拓宽光伏光热系统在建筑中的应用。本文提出4种光伏光热墙体,针对夏季工况,对4种光伏光热墙体的出口温度、空气得热量、光伏板表面温度进行模拟。
2 物理模型
光伏光热墙体高×宽×厚为1 700 mm×1 000 mm×304 mm。由室外到室内依次为:玻璃盖板、光伏板、空气通道、砖墙。玻璃盖板高×宽×厚为1 700 mm×1 000 mm×4 mm。光伏板长×宽×厚为1 000 mm×700 mm×4 mm,安装在墙体高度中间部分。空气通道进、出口截面尺寸均为1 000 mm×100 mm。砖墙高×宽×厚为1 700 mm×1 000 mm×200 mm,当设置相变材料时砖墙厚度含相变材料厚度(60 mm)。4种光伏光热墙体物理模型见图1。各模型均由玻璃盖板、光伏板、空气通道、砖墙组成,模型1、2的光伏板紧贴玻璃盖板内侧,模型3、4的光伏板置于空气通道中间,模型2、4在砖墙一侧增设相变材料层。相变材料选用石蜡,光伏光热墙体各种材料的热物性参数见表1。空气密度由数学模型计算得到。
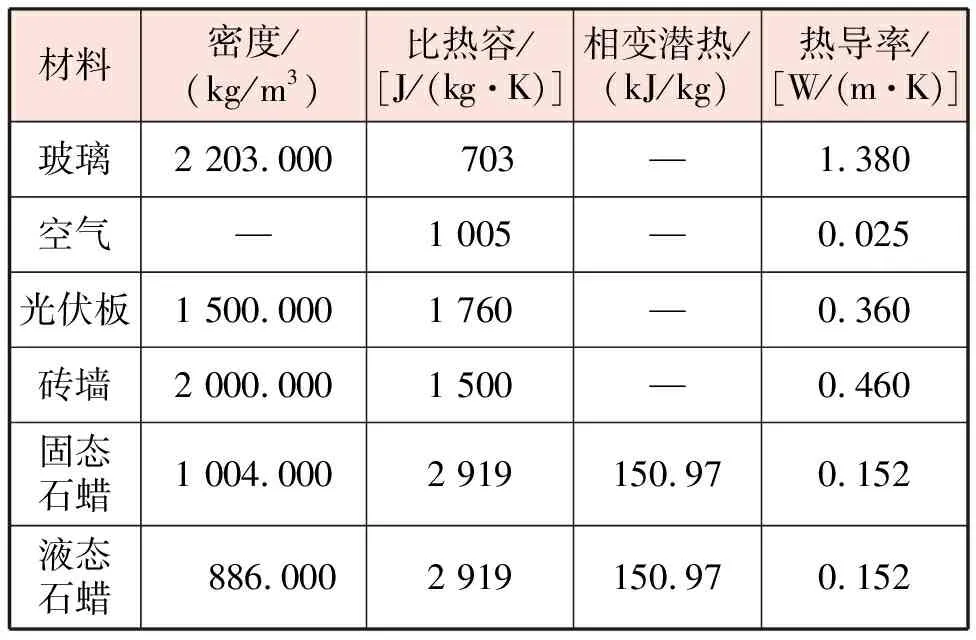
表1 光伏光热墙体各种材料的热物性参数
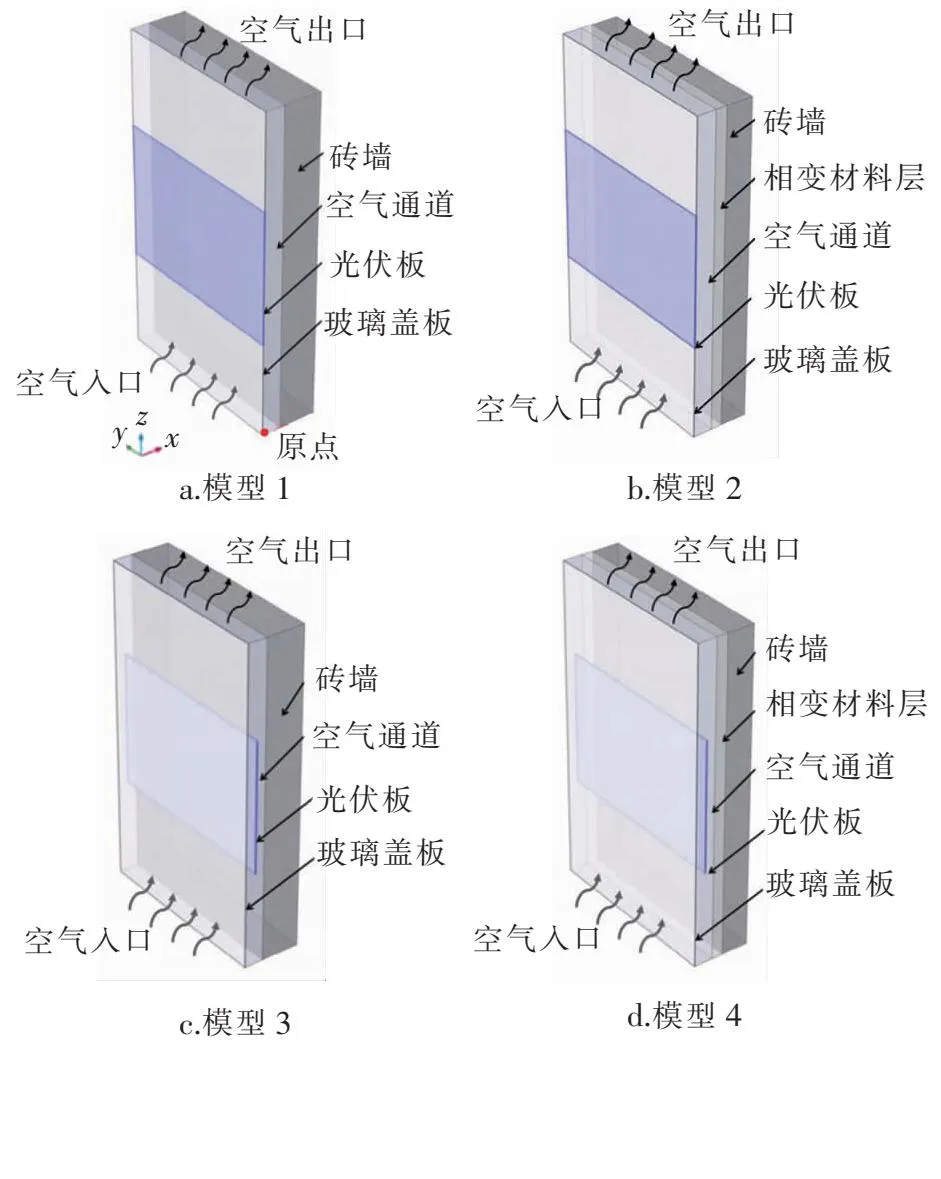
图1 4种光伏光热墙体物理模型
3 数学模型
3.1 主要数学方程
光伏墙体的热量传递主要是沿着墙体厚度方向。为简化计算,进行以下设定:光伏墙体内各层材料均为各向同性。相变过程中,相变材料除了密度发生变化外,比热容、热导率均不变。不考虑相变材料固液两相之间的对流。忽略光伏墙体各层材料之间的接触热阻。
① 空气层
连续性方程:
div(ρu)=0
(1)
式中 div——散度
ρ——空气密度,kg/m3
u——空气速度矢量,m/s
动量方程:
ρ(udivu)=-divp+divμ(gradu)
(2)
(3)
(4)
式中u——空气速度分量,m/s
p——空气压力,Pa
μ——空气动力黏度,Pa·s
grad——梯度
k——湍流动能,J
μT——湍流黏性系数,Pa·s
σk——模型常数,取1.00
Pk——湍流动能生成项
ε——湍流耗散率
σε——模型常数,取1.30
C1——模型常数,取1.44
C2——模型常数,取1.92
② 砖墙传热方程
砖墙接收太阳能,热量的传递过程主要为导热,传热方程为:
(5)
式中ρw——墙体材料密度,kg/m3
cw——墙体材料比热容,J/(kg·K)
θw——墙体材料温度,K
t——时间,s
λ——墙体材料热导率,W/(m·K)
Q——热源项,指吸收的太阳辐射热,W/m3
光伏板吸收太阳辐射后,与空气层内空气对流传热。玻璃盖板外表面与室外空气对流传热,玻璃盖板内表面与空气层内空气对流传热,玻璃盖板视为通过大平壁的一维导热。
相变材料的能量方程为:
h=hs+hL
(6)
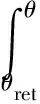
(7)
hL=fHi
(8)
f=0,θ≤θs
(9)
(10)
f=1,θ≥θL
(11)
式中h——相变材料比焓,J/kg
hs——相变材料显热比焓,J/kg
hL——相变材料潜热比焓,J/kg
θ——相变材料温度,℃
θret——相变材料初始温度,℃
cPCM——相变材料比热容,J/(kg·K)
f——液相率
Hi——相变潜热,J/kg
θs——相变材料凝固温度,℃,本文取26 ℃
θL——相变材料熔化温度,℃,本文取28 ℃
3.2 模拟软件
笔者采用COMSOL软件进行模拟,建立光伏光热墙体的三维模型。模型主要考虑辐射传热、固体部件内部传热、流体的湍流和外界环境的对流。模型将传热方程与流体流动的N-S方程和连续性方程进行耦合。
3.3 边界条件与初始条件
玻璃盖板外表面与室外空气进行对流传热,玻璃盖板外表面传热系数为1.0 W/(m2·K)。砖墙内壁面与室内空气进行对流换热,砖墙内壁面表面传热系数为1.5 W/(m2·K),室内环境温度设为25 ℃。除空气通道进出口外,光伏光热墙体四周均为绝热条件,空气通道进口风速变化范围为0.1~0.5 m/s。模型初始状态温度为25 ℃,进风温度为室外温度。室外温度、太阳辐照度随时间的变化见图2[13]。图中时段编号7表示[6:00,7:00),时段编号8表示[7:00,8:00),以此类推。模拟时间为7:00—24:00。
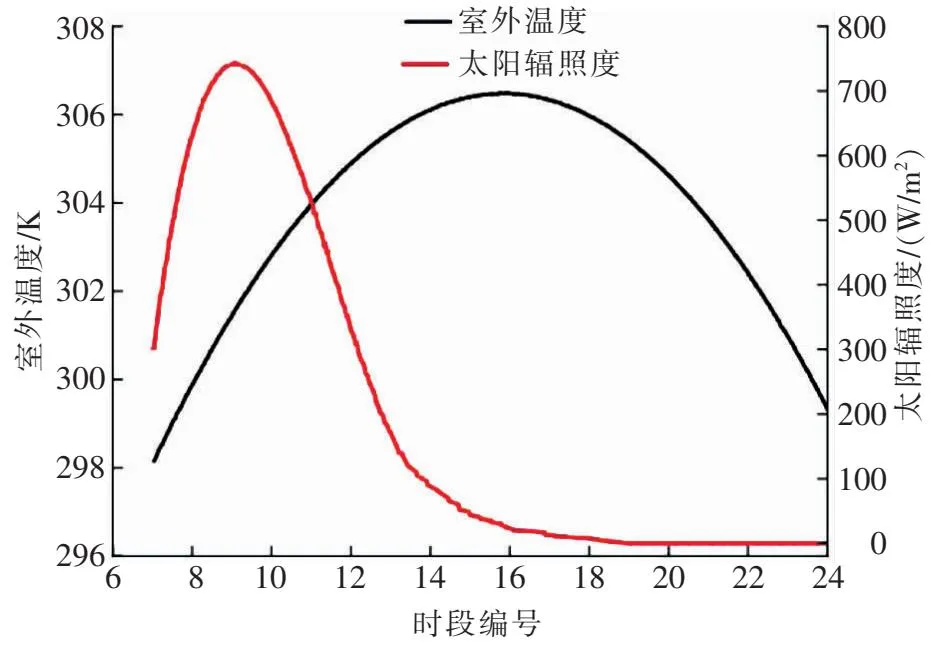
图2 室外温度、太阳辐照度随时间的变化
3.4 网格无关性验证
模型采用自由四面体进行网格划分,在各层边界处对网格进行加密处理。进口风速为0.1 m/s,各模型不同网格数10:30时空气通道出口温度见表2。由表2可知,当网格数超过51 267后,随着网格数增加,出口温度变化很小,说明网格数继续增加对模拟计算结果的影响可以忽略。因此,为平衡计算时间和精度,模型网格数选取51 267。

表2 各模型不同网格数10:30时空气通道出口温度
3.5 模型验证
为验证模型的准确性,建立与文献[14]的特朗伯墙相同结构的物理模型。在进口风速为1 m/s条件下,采用本文的模型模拟出口温度,并与文献[14]的实验出口温度进行比较。室外温度、太阳辐照度来自文献[14]。模拟出口温度与实验出口温度见图3。由图3可知,模拟出口温度与实验出口温度变化趋势一致。与实验出口温度相比,模拟出口温度的最大相对误差绝对值为4.29%。因此,模型的准确性比较高。

图3 模拟出口温度与实验出口温度
4 模拟结果与讨论
4.1 出口温度、空气得热量
① 出口温度
进口风速为0.1、0.5 m/s时,模型1~4出口温度分别见图4、5。由图4、5可知,出口温度受室外温度、太阳辐照度综合影响。各模型的出口温度均随进口风速增大而整体下降。进口风速一定时,模型3出口温度最高。
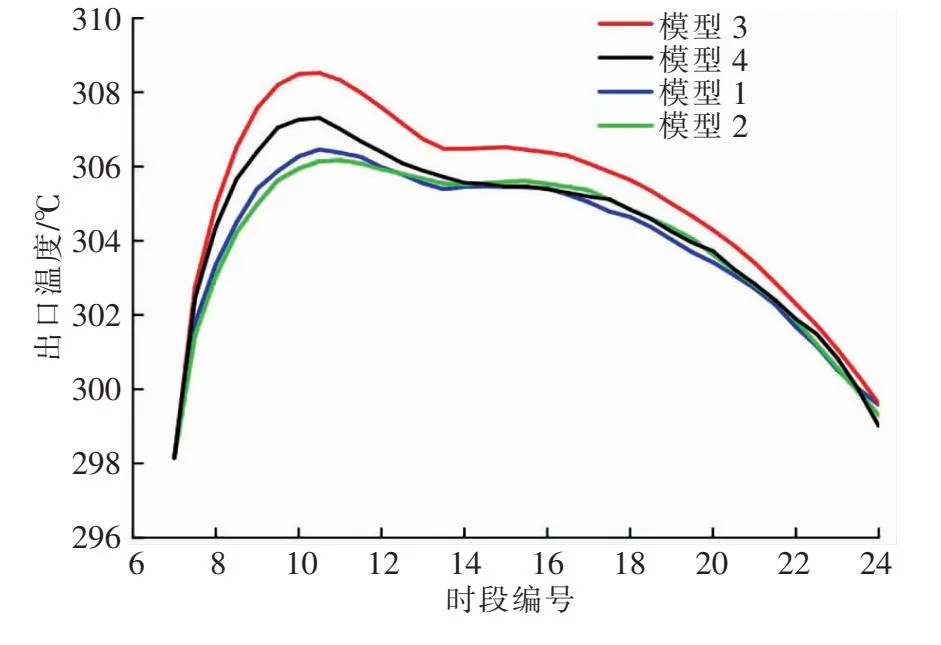
图5 进口风速为0.5 m/s时模型1~4出口温度
② 空气得热量
进口风速为0.1、0.5 m/s时,模型1~4空气得热量分别见图6、7。空气得热量根据空气进出口温差、空气质量流量计算得到。由图6、7可知,各模型空气得热量变化趋势与出口温度变化趋势基本一致。进口风速一定时,模型3空气得热量最高,模型1、2、4的空气得热量接近。
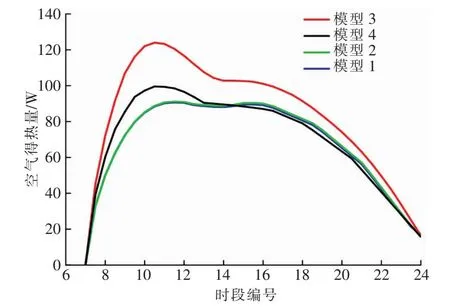
图6 进口风速为0.1 m/s时模型1~4空气得热量

图7 进口风速为0.5 m/s时模型1~4空气得热量
4.2 光伏板表面温度
进口风速为0.1 m/s,10:30各模型光伏板表面(向阳面)温度分布见图8,图中表面温度的单位为K。由图8可知,相同条件下,光伏板表面温度由低到高的排序为模型4、模型3、模型2、模型1。这主要是由于模型4的光伏板置于空气通道中间且相变材料层发挥了吸热作用。
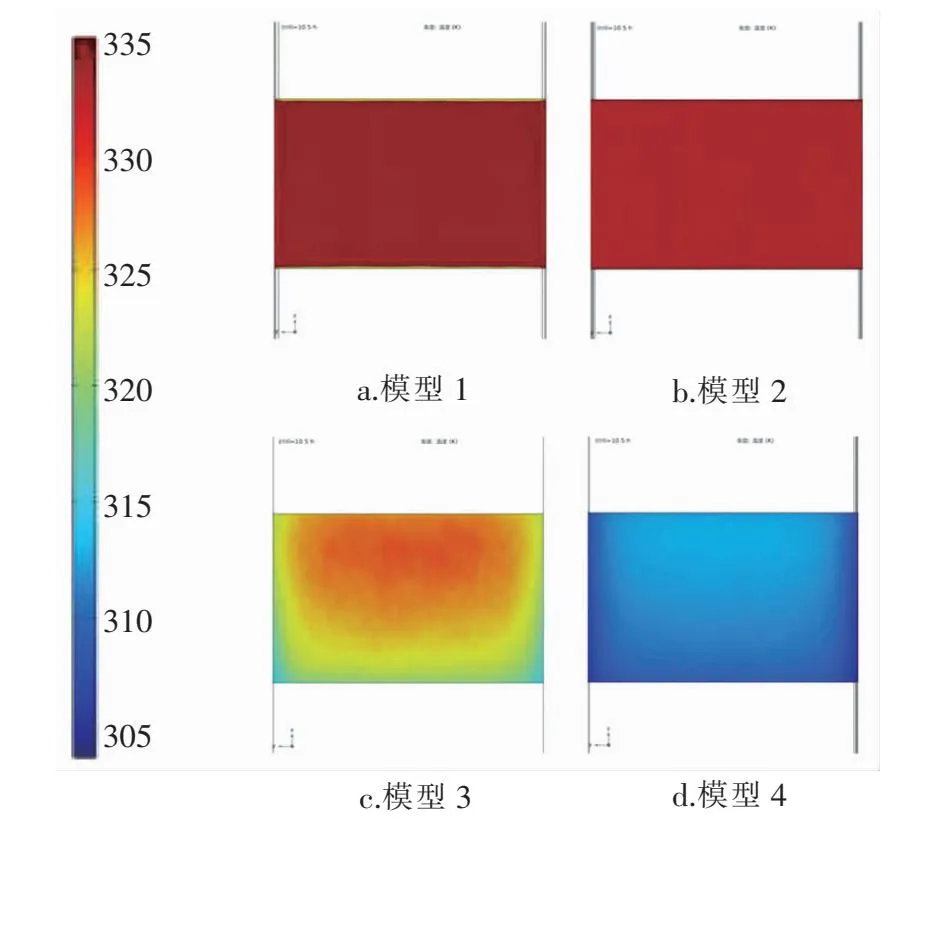
图8 进口风速为0.1 m/s时10:30各模型光伏板表面温度分布(软件截图)
由模拟结果可知,进口风速为0.1 m/s时,在有太阳辐射时段,模型4光伏板平均表面温度在4种模型中最低,模型3仅高于模型4。
4.3 综合性能分析
由上述分析可知,模型3能够在较小的进口风速下得到较高的空气出口温度及较高的空气得热量。在4种模型中,模型3光伏板表面温度低于模型1、2,仅高于模型4,有利于提高光电转换效率。因此,模型3的综合性能最佳。
5 结论
在较小的进口风速下,模型3能得到较高的空气出口温度及较高的空气得热量。模型3光伏板表面温度低于模型1、2,仅高于模型4,有利于提高光电转换效率。模型3的综合性能最佳。
