平顶型CLPG-CFBG级联结构中温度应力传感特性的研究
2024-04-03吕子尚胡劲华任丹萍赵继军
吕子尚,胡劲华,任丹萍,赵继军
(河北工程大学 信息与电气工程学院,邯郸 056038,中国)
0 引 言
光纤光栅凭借不受外部光源波动影响、传感信号强、检测精度高、响应频率快、抗干扰检测能力强,以及器件组网方式灵活等优点,已日益成为光纤信息通信和光纤传感网系统的关键器件之一[1]。在分布式光纤传感网系统中,由于光纤光栅传感器对温度[2-4]、湿度[5]、微弯曲应变[6]和应力[7]等多个参量都非常敏感,被广泛用于矿井安全、结构健康监测[8]和周界安防等领域进行环境参量的监测和传感。物体特性变化时最直观的表现方式体现在温度和应力两方面,这使得一个传感器能够实现温度和应力同时检测显得尤为必要。因此,研究者们通过设计不同类型的光纤光栅结构形成两个或多个谐振峰,利用不同类型谐振峰之间对介质温度/应变测量的灵敏度大小不同实现双参量的同时检测。例如,GUO等人[9]提出了一种少模光纤长周期光栅双参量传感,利用模式间双峰耦合现象提高了测量灵敏度。ZHANG等人[10]采用单模和多模光纤级联的方式制备了一种新型高灵敏度的多模光纤啁啾长周期光栅,利用两个高阶模透射谱对两种参量的响应差实现了同时传感。KANG等人[11]利用耦合型双芯光纤对外界温度和应力变化的灵敏度响应特性与光纤布喇格光栅(fiber Bragg grating,FBG)的不同提出了一种新的传感器,且耦合型双芯光纤的应力和温度灵敏度达到了0.98867 pm/με和31.25 pm/℃,FBG则分别达到了1.25 pm/με和10.125 pm/℃。ZHANG等人[12]提出了长周期光纤光栅(long period grating,LPG)与FBG级联的双参量传感器结构,形成了3个谐振峰,在一定测量范围内使温度和应力灵敏度最大分别达到了41.66 pm/℃和2.33 pm/με。
在光纤传感系统中,光纤光栅传感器不仅要解决温度应力之间存在的交叉敏感问题,还需满足光纤通信中色散补偿[13]和稳定传输波段[14]的要求。啁啾光纤光栅由于光栅的周期沿光纤轴呈线性分布,使得光脉冲展宽形成平顶光谱[15],可以有效地实现色散补偿[16],并且对环境温度和应力的变化也较为敏感[17]。上述光纤光栅传感器的输出光谱为洛伦兹型,中心波长随温度和应力的变化均会漂移,但没有稳定的通信传输波段,容易产生色散,影响通信的传输质量,不利于系统通信传感一体化[18]。
因此,本文作者提出了一种基于啁啾长周期光纤光栅(chirped long period grating,CLPG)[19]和啁啾光纤布喇格光栅(chirped fiber Bragg grating,CFBG)[17]级联的平顶型温度应力双参量光纤光栅传感器。通过优化调节所提出结构中的啁啾系数大小,增大光谱带宽,输出平顶透射光谱,形成稳定的传输波段,以保证光信号的传输质量。利用CLPG和CFBG形成的不同谐振峰对温度和应力灵敏度响应不同的特性,有效地消除了两种参量检测时的交叉敏感,使传感器实现了温度应力的同时传感,并从模场能量角度分析了包层半径变化对CLPG灵敏度影响。该传感器有望与现有的光通信基础设施进行很好的兼容,实现通信传感一体化[20],在分布式光纤传感系统中具有良好的应用前景。
1 器件结构与原理
图1为本文作者提出的一种平顶型温度应力双参量传感的器件结构示意图。该器件由 CLPG和CFBG共同级联而成,器件结构主要元件的基本物理结构参数分别为:纤芯折射率n1,包层折射率n2,CLPG初始周期Λ0,l,CFBG初始周期Λ0,B,CLPG长度Ll,CFBG长度LB,纤芯半径r1,包层半径r2。光由左侧输入,由于啁啾光纤光栅的周期呈啁啾性变化,入射光谱经传感器变化后输出为平顶型光谱。
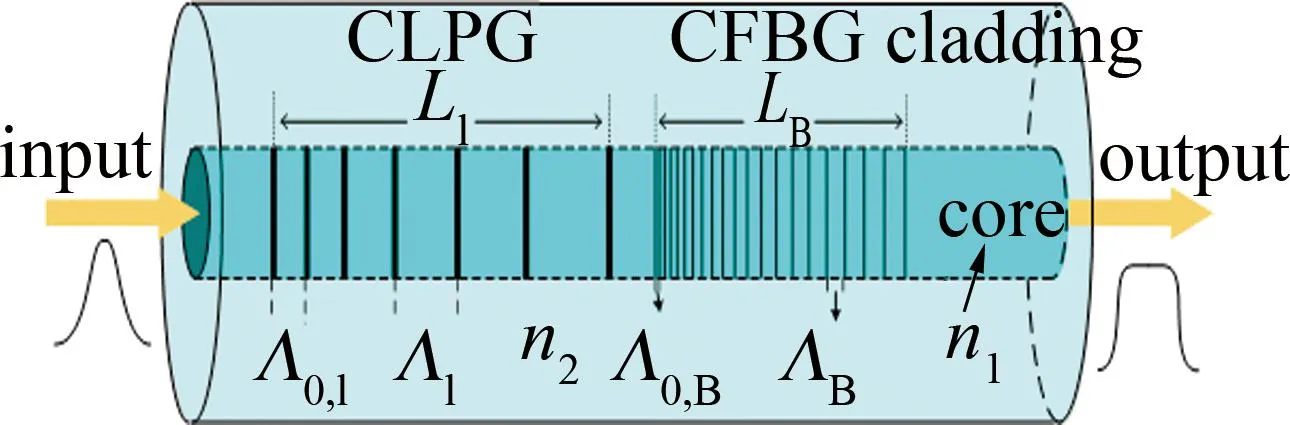
图1 CLPG-CFBG级联结构示意图Fig.1 Schematic diagram of the CLPG-CFBG cascaded structure
基于耦合模理论可知,CLPG光谱是由纤芯基模和高阶的包层模式之间相互耦合形成的正向传输的透射光谱。所以CLPG谐振波长λl表达式如下[10,21]:
λl=(neff,1-neff,2)Λl
(1)
式中:neff,1为纤芯基模有效折射率;neff,2为包层模式的有效折射率;Λl为CLPG的啁啾周期。而CFBG与FBG相同为正向纤芯模式和反向纤芯模式的自耦合现象,依据相位匹配条件可得CFBG的谐振波长λB为[21]:
λB=2neff,1ΛB
(2)
式中:ΛB为CFBG的啁啾周期。啁啾周期是由于光栅条在光纤中呈线性分布形成的,因此可得啁啾光纤光栅周期Λ表达式:
Λ=x(c/L)+Λ0-c/2
(3)
式中:Λ0为啁啾光纤光栅周期的初始值;c为啁啾光纤光栅啁啾系数;x为啁啾周期在对应啁啾光纤光栅长度中所在的位置,且范围为0≤x≤L;L代表对应的啁啾光纤光栅长度。
由弹性力学和弹光效应理论可知,在外界应力发生改变作用在光纤光栅轴向方向时,纤芯和包层各介质本身的有效折射率均会受到轴向应力的影响,同时光栅周期也会随应力的变化而变化。因而当光纤轴向应力ε发生改变时,对长短周期的谐振波长式(1)、式(2)取微分可以得出各自谐振中心波长对应的应力灵敏度系数,其表达式为[22]:

(4)
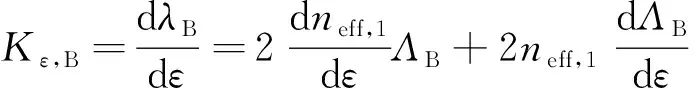
(5)
式中:Kε,l、Kε,B分别为CLPG应力灵敏度系数和CFBG应力灵敏度系数。应力对光纤有效折射率neff的影响主要取决于光纤光栅本身的弹光系数Pe的大小,即dneff/dε=neff×Pe[9];对啁啾光纤光栅周期的影响为dΛ=Λdε[10]。因此当作用在传感器轴向方向的应力大小变化量为Δε时,依据式(4)、式(5)所求出的Kε联立等式,可计算出传感器中心波长位移量大小Δλ为:
Δλ=Kε×Δε
(6)
同应力变化相似,当外环境温度T发生变化时,周期受自身材料热膨胀系数η=Λ-1dΛ/dT[7]的影响、有效折射率受热光系数ξ=neff-1dneff/dT[7]的影响。对式(1)和式(2)取温度的微分得到温度灵敏度系数[21]:

(7)
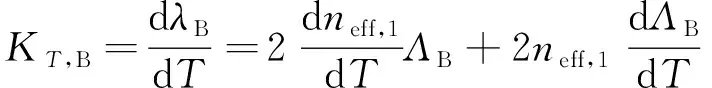
(8)
因此,当传感器周围环境温度的变化量大小为ΔT时,依据式(7)、式(8)所求出的KT与温度变化量联立等式可计算出传感器中心波长位移量大小Δλ为:
Δλ=KT×ΔT
(9)
综上所述,当传感器受到外环境温度和自身轴向应力的同时作用时,联立式(6)、式(9)生成方程组,进而生成传输矩阵方程为:

(10)
式中:Δλl表示为CLPG的中心波长位移量;ΔλB表示CFBG中心波长的位移量,且灵敏度系数矩阵行列式D=|Kε,lKT,B-KT,lKε,B|≠0。因此通过观察中心波长位移量,结合逆系数矩阵可知温度和轴向应力各自的变化量大小,即式(10)的逆传输矩阵:

(11)
2 器件设计与分析
首先对级联CLPG-CFBG传感器初始结构参数设置介绍如下:n1=1.45、n2=1.46[23],器件纤芯半径r1=4.15 μm,CLPG周期初始值Λ0,l=220 μm,CFBG周期初始值Λ0,B=0.49 μm。光纤光栅的调制系数随刻蚀的深度加深而增大,进而使得光纤光栅的透射谱越明显,因此在合适范围内CLPG调制系数设为0.0005,CFBG调制系数为0.0008,CLPG长度Ll=3.5 cm,CFBG长度LB=2 cm。
2.1 啁啾系数选择
为了满足在光纤传感系统中的应用,得到更好的平顶透射光谱谱型。依据式(3)分别讨论了CFBG的啁啾系数cB和CLPG的啁啾系数cl各自在不同数值大小时对透射谱的影响。从图2a可知,在0.001~0.003范围内,随着cB的增大,CFBG的透射光谱带宽逐渐展宽;但是当cB到达0.002以后,随着啁啾系数的增大,透射率效果反而减小。由分析可知,当cB=0.002时,CFBG的透射平顶光谱最好,且平顶带宽达到了5.6 nm。同理,CLPG的平顶光谱在光纤传感系统中有利于宽带模式的转换促进模式之间的耦合[24],提高光纤内模式耦合效率[25],对CLPG的啁啾系数cl在4.1~4.7范围内进行了仿真分析。由图2b所示,cl的数值大小变化对CLPG透射光谱带宽没有影响,CLPG平顶光谱带宽达到了13.8 nm;但是当啁啾系数cl=4.4时,透射光谱平顶效果最好。由此可知,当cl=4.4、cB=0.002时,两平顶光谱分别达到最优效果。
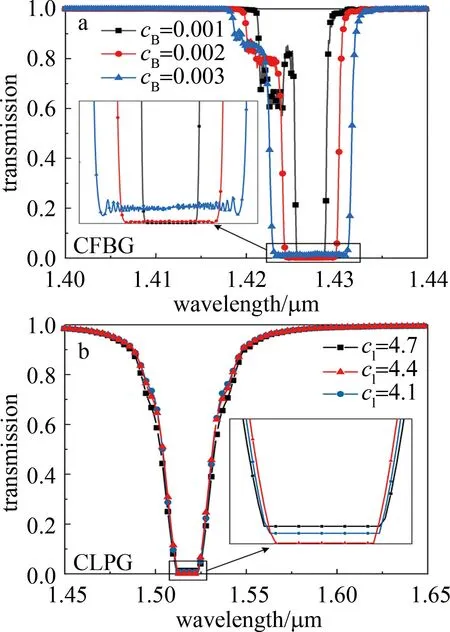
图2 啁啾系数分析光谱图Fig.2 Spectrogram of the chirp coefficient analysis
2.2 包层半径选择
随后,进一步研究CLPG-CFBG级联结构中包层半径对谐振中心波长漂移的影响,仿真分析了不同半径下,该器件结构截面的模场分布。如图3所示,本文中将包层半径r2从62.5 μm逐渐减小到15.5 μm,对比观察两种模式在不同半径下的模场能量分布情况。由图3a、图3b和图3c可以观察到纤芯基模(LP0,1)模场能量保持不变,不受包层半径的影响。观察图3d、图3e、图3f可知,随包层半径的减小,1阶2次包层模(LP0,2)模场能量分布逐渐减小,这使得该光纤光栅传感器结构周围介质中的消逝波增大[26],光纤光栅传感器与外界环境的相互作用[27]增强,有利于提高光纤光栅传感器对温度和应力检测的灵敏度。
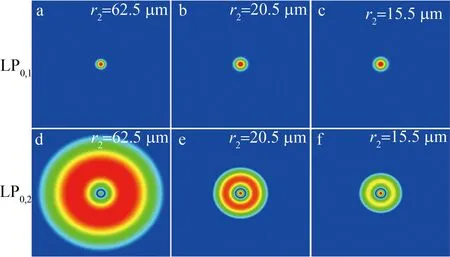
图3 不同包层半径下CLPG-CFBG传输模式的模场能量分布Fig.3 Mode-field distribution of CLPG-CFBG transmission modes at different cladding radii
另外,光纤光栅的模式主要由纤芯和包层的模式有效折射率决定,因此仿真计算了不同包层半径下两种模式分别对应的有效折射率。如表1所示,随包层半径的减小,LP0,1模的有效折射率不变,LP0,2模的有效折射率值逐渐减小,与模场能量变化规律相符合。依据式(1)可知,在相同环境影响下,neff,1和neff,2的差值越大,CLPG的谐振中心波长漂移越明显,环境参量检测时的灵敏度越高。但是CLPG透射光谱是纤芯模与包层模相互耦合的效果,包层半径小于20.5 μm时,CLPG光谱透射效率反而降低,所以包层半径选定为20.5 μm。

表1 不同包层半径下两种模式的有效折射率值Table 1 Effective refractive index values of the two modes at different cladding radii
级联型结构传感器输出光谱形状如图4所示。从图中可知,平顶带宽较窄的谐振峰表示CFBG结构光谱,右侧谐振峰平顶带宽较宽,为CLPG结构光谱。
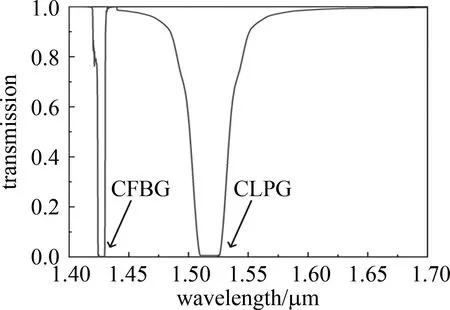
图4 CLPG-CFBG级联结构透射光谱Fig.4 Transmission spectrum of the CLPG-CFBG cascaded structure
3 结果与分析
3.1 应力传感特性
随着轴向应力的增加,两个谐振峰漂移呈不同的漂移趋势。如图5a和图5b所示,CLPG的谐振峰中心波长位置随应力的增大向短波长方向蓝移,CFBG的谐振峰中心波长位置随应力的增大而红移,因此使得两中心波长之间间距减小。为了更准确地测量出谐振中心波长随应力变化的规律,从0 με~500 με范围内每100 με进行取点采样,如图5c和图5d所示。波长漂移与应力变化呈良好的线性关系,并计算出CFBG的应力灵敏度Kε,B=0.8 pm/με,线性度R2=0.99865;CLPG的应力灵敏度Kε,l=-132 pm/με,线性度R2=0.99981。
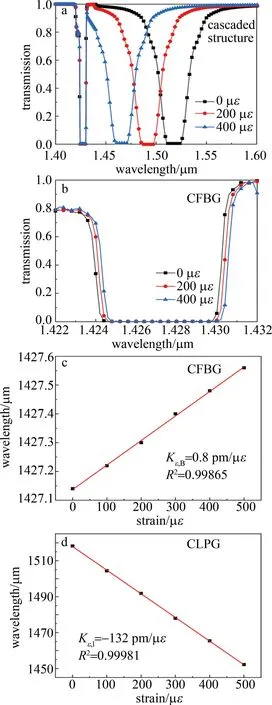
图5 应力测量Fig.5 Strain measurement
3.2 温度传感特性
随着外界温度的升高,两个谐振峰中心波长位置呈相同的漂移趋势,与应力相反。如图6a和图6b所示,CLPG和CFBG的谐振峰均同时向长波长方向红移,中心波长间距增大。为了更准确地测量出谐振中心波长随温度升高的变化规律,从20 ℃~80 ℃每10 ℃进行取点采样,对各个采样点进行多次测量求平均值,随后将各平均值进行线性拟合。如图6c和图6d所示,波长漂移的大小与温度变化量呈良好的线性关系。由此计算出CFBG的温度灵敏度KT,B=12.6 pm/℃,线性度R2=0.99938;CLPG的温度灵敏度KT,l=2660 pm/℃,线性度R2=0.99998。
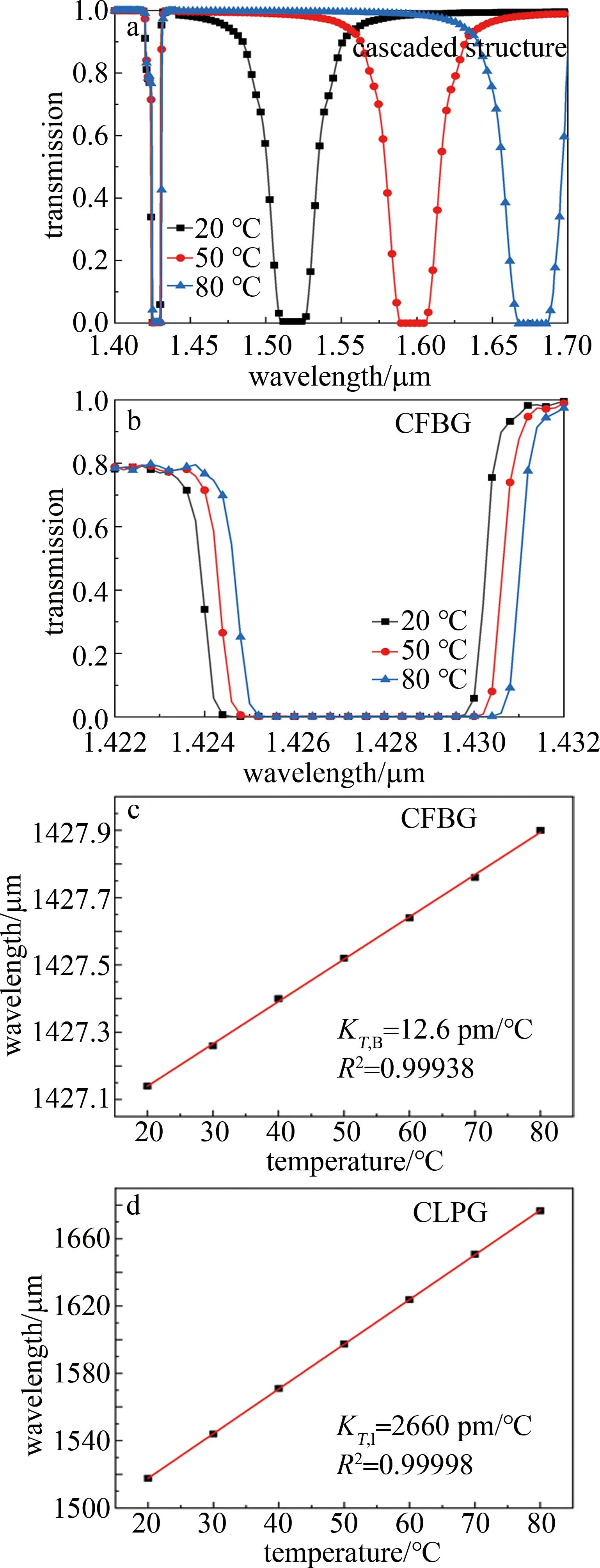
图6 温度测量Fig.6 Temperature measurement
综上所述,将仿真结果Kε,l=-132 pm/με、KT,l=2660 pm/℃、Kε,B=0.8 pm/με、KT,B=12.6 pm/℃代入式(11),得到逆传输矩阵方程:

(12)
当外界环境温度和应力发生变化时,通过观察两个谐振中心波长的变化量并代入式(12),可以直接计算出温度和应力的变化量。
此外,外界温度和应力在一定范围内变化时,CFBG平顶光谱总是存在固定的部分重叠光谱,重叠波段在1426 nm~1429 nm之间,如图5b和图6b所示。因此该部分重叠光谱可以为光信号通信提供稳定的传输波段,保证了光信号通信的传输质量,可更好地与现有的通信基础设施相结合,有利于通信传感一体化进程。
4 结 论
本文中提出了一种CLPG-CFBG级联平顶型光纤光栅传感器结构。仿真结果表明,CLPG的温度和应力灵敏度分别为2660 pm/℃和132 pm/με,CFBG的温度和应力灵敏度分别为12.6 pm/℃和0.8 pm/με,生成了灵敏度系数矩阵,有效解决了温度和应力之间相互存在的交叉敏感问题,使传感器具有双参量同时传感的功能。进一步优化光纤的啁啾系数,使CLPG和CFBG的平顶光谱带宽分别达到了13.8 nm和5.6 nm。在一定温度和应力传感范围内,具有1426 nm~1429 nm范围内稳定传输的通信波段,可以保证光信号的传输质量。与传统传感器相比,该传感器具有温度应力双参量传感和稳定通信传输的功能,能够更好地与通信基础设施相结合应用于光纤传感网系统中。
