大功率燃料电池建模与电压一致性分析

2024-04-02包敏杰俞小莉陈俊玄陈孝炀郅文彬

储能科学与技术 2024年3期

包敏杰，俞小莉，黄瑞，陈俊玄，陈孝炀，郅文彬

（1浙江大学工程师学院，浙江杭州 310015；2浙江大学能源工程学院，浙江杭州 310027；3浙江省汽车智能热管理科学与技术重点实验室，浙江台州 317299）

随着人类对环境保护的重视程度提高，一系列政策的制定推动着燃料电池普及与应用[1]。其中质子交换膜燃料电池，凭借其功率密度高、体积小以及工作温度低等特点，广泛运用于燃料电池车以及储能场景中[2]。然而燃料电池对工作温度要求苛刻，长期处于过高或过低温度工作的电池，其寿命将显著短于其他工作在正常温度的电池，这也会导致燃料电池堆的“短板效应”显现，使得电池堆的寿命将由寿命最短的单体决定。燃料电池堆在工作时由于结构布置、运行状态和冷却方式不同等原因，存在温度分布不均匀的问题。并且随着车用燃料电池的应用，燃料电池也将朝着大功率发展，大功率燃料电池的热分布特性将变得不同，局部一致性变差的问题更加凸显[3]。

目前对于燃料电池单体一致性的研究主要采用仿真方式进行。现有常见的燃料电池堆仿真研究方法包括建立燃料电池堆的一维模型[4-5]、二维模型[6-7]和三维模型[8-9]。Baschuk等[4]建立了含50个单体电池的流体网络模型，仿真结果表明，通过增加歧管的尺寸，减少每个双极板的气体流动通道的数量，以及合理地改变气体流动通道中的流阻，有助于燃料电池堆内反应物的均匀分布。赵岩等[5]采用燃料电池流道简化方法和压力速度耦合算法数学模型对30～50 节燃料电池进行仿真，仿真结果表明采用Z形结构的空气分布均匀性比U形好，并且增加歧管宽度有利于改善气体分布。Yang 等[6]基于Z 形歧管，考虑每个燃料电池内部的流量分布以及反应、相变和传输过程，建立了包含5节单体的1+1维多相电堆子模型和流量分布综合电堆模型，仿真结果表明，增加入口压力对反应物分布均匀性的影响不大，但它提高了电堆工作性能，并且采用更大的歧管横截面积能够使电池之间的反应物分布更均匀。同时Yang等[7]建立了考虑了摩擦和局部压降损失以及膜水、液态水、气体组分和热量的耦合传输过程的二维电堆模型，通过仿真发现如果歧管的横截面积相对较小，U形结构可以比Z形结构获得更好的反应物分布均匀性，这有助于减小整个电堆的几何尺寸。Asgharian等[8]建立了考虑双极板流道的歧管10 节燃料电池三维模型，通过CFD 仿真，结果表明歧管的直径增加能够使流道中气体分布更均匀。Huang等[9]建立含100、200、300个单体燃料电池的歧管三维模型，基于CFD 仿真的手段，结果表明，随着燃料电池个数增加和工作电流增大，歧管流量分布更加不均匀。

目前针对燃料电池的建模仿真，大部分研究只考虑了燃料电池气体歧管结构、电压或温度其中某一个或者某几个因素。针对燃料电池堆性能一致性的研究，多数研究主要聚焦在流量分布上，而电池堆实际工作时，气体流量、电压和温度之间存在耦合关系，相互影响。并且现有研究的燃料电池存在功率小的问题，而针对大功率电池堆性能一致性的变化规律尚未明确。

因此针对以上存在的问题，本工作以某款110 kW 大功率燃料电池为研究对象，建立考虑流量、电压和温度分布的燃料电池多参数耦合模型，通过燃料电池稳态试验对模型进行验证，并且基于该模型仿真结果探究不同运行参数对燃料电池单体电压一致性的影响规律。本研究旨在提高燃料电池工作时单体性能的一致性并提高燃料电池的使用寿命，为后续燃料电池堆结构优化设计和热管理策略设计提供指导。

1 燃料电池理论模型建立

本工作所建立的燃料电池模型包括：流体网络模型、燃料电池电压模型和燃料电池热阻模型三部分。首先将燃料电池初始温度以及总的气体流量代入流体网络模型计算并更新单体气体分布结果，其次将单体气体分布结果代入燃料电池电压模型计算并更新单体电压结果，最后将电压结果代入燃料电池热阻模型计算并更新温度，而温度也会影响气体流量和电压结果，因此需要进行迭代计算，并且在模型当中额外考虑了流道结构的局部损失、冷却水流量分布和燃料电池接触热阻等因素的影响。

1.1 流体网络模型

本工作所研究的110 kW 大功率燃料电池堆的阳极歧管、阴极歧管和冷却水歧管布置均采用“U形”结构布置即流体的进口和出口在同一侧，其中阳极歧管和阴极歧管进出口均在电堆的右侧，冷却水进出口在电堆的左侧，如图1所示。

图1 大功率燃料电池堆歧管布置方式Fig.1 Manifold arrangement for high power fuel cell stacks

流体网络模型主要用于计算阳极气体、阴极气体以及冷却水的流量分布，由于计算流程和内容相似，本工作以阳极和阴极气体为例。如图2所示的“U 形”流体网络图，反应气体从进气歧管进入，然后分配到每一个电池，最后从排气歧管流出，在流动过程中反应物的物性参数会受到单体温度的影响，同时遵循能量守恒定律和质量守恒定律，通过计算得到反应气体在每块电池中的质量流量，为后续构建燃料电池电压模型提供输入[10]。

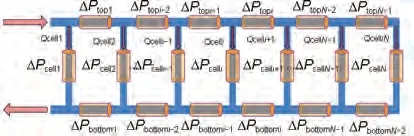
图2 “U形”燃料电池堆流体网络图Fig.2 "U-shaped" fuel cell stack fluid network diagram

根据能量守恒定律，在反应物流动的过程中，相邻的两个电池之间压力损失关系为：

燃料电池压降的计算如公式(2)所示：

式中，∆Pm,loss为反应物消耗的质量损失；∆Pm为局部损失；∆Pf为沿程损失。

其中反应物消耗的质量损失∆Pm,loss为：

式中，Amani为气体流道的截面积，m2；mcell,in和mcell,out分别为流入电池和流出电池的气体流量，kg/s。

其中沿程损失∆Pf为:

式中，L为管道长度，m；v为反应气体速度，m/s；d为管道的水力直径，m；Cf为摩擦系数。

在进排气歧管处的局部损失∆Pm主要是由于分叉、汇集和弯管处的造成[11]。

将公式(3)和(4)代入公式(2)可以得到压降计算公式为：

同时由于电池内部反应的消耗导致流道出口处和进口处的质量流量不一致，存在下述的关系。

式中，mr为反应消耗的质量流量，kg/s 。

由于阴极和阳极的反应方程式不同，因而消耗的质量流量有差异。阳极消耗氢气，且生成物氢离子通过质子交换膜到阴极处；阴极处氧气被消耗，同时会产生液态水。

式中，I为电池堆电流密度，A/m2；Acell为燃料电池的活化面积，m2；Mx为物质x 的摩尔质量，kg/mol。

1.2 燃料电池电压模型

通过上文流体网络模型计算得到流入每块电池的氢气和空气质量流量以及单体温度分布，为接下来计算燃料电池电压提供输入参数。

燃料电池的实际输出电压可通过理想电压和极化损失电压得出[12-15]：

式中，Enernst为能斯特电动势，V；Vact为活化极化电动势，V；Vohm为欧姆极化电动势，V；Vconc为浓度差极化电动势，V。

能斯特电动势计算公式如下：

式中，PH2和PO2为氢气和氧气的有效分压，kPa。

活化极化电动势计算公式如下：

式中，i为电池堆电流，A；ξ1、ξ2、ξ3、ξ4为比例系数，CO2为电极与膜接触面上的氧气浓度，可以由亨利定律得到。

λm为膜的含水量，一般在0～14之间变化，主要由相对湿度φ决定：

浓度差极化电动势计算公式如下：

此时将公式(10)～(16)代入公式(9)，即可得到每块电池的电压。

1.3 燃料电池热阻模型

通过燃料电池电压模型得到每块电池的电压以后，即可计算出每块电池的产热，本研究建立了带有散热模块的电池堆热阻模型。散热形式是在相邻两个单电池中间加入一个冷却板。

燃料电池主要产热的区域是在阴极催化层内，H+通过之间的交换膜，到达阴极催化层与O2发生还原反应，产生由于反应熵变引起的可逆热，燃料电池堆产生的热量Q为：

式中，Ncell为燃料电池的个数；U为燃料电池堆的工作电压，V；F为法拉第常量，96485 C/mol；∆H为反应热，285.8 kJ/mol。

图3所示为燃料电池热阻模型示意图，燃料电池的热阻主要包括材料自身的导热热阻和每一层之间的接触热阻，它们之间是串联关系。其中燃料电池的导热热阻主要有五个部分：阴极与阳极双极板、阴极与阳极气体扩散层、阴极与阳极微孔层、阴极与阳极催化层以及质子交换膜。其热阻的计算如公式(18)所示：

图3 燃料电池热阻模型示意图Fig.3 Schematic of fuel cell thermal resistance model

式中，δ为燃料电池各层的厚度，m；A为燃料电池各层的面积，m2；λ为燃料电池各层的热导率，W/(m∙K)。

燃料电池的接触热阻主要有四个部分：气体扩散层和双极板之间的接触热阻、气体扩散层和微孔层之间的接触热阻、微孔层和催化层之间的接触热阻以及催化层和质子交换膜之间的接触热阻。其中气体扩散层和微孔层之间的热阻常用在微孔层和扩散层之间增加一层微孔层-扩散层集成区来代替[16]。由于催化层与气体扩散层和质子交换膜接触好、接触热阻较小，计算时可以忽略这部分热阻[17]。

同时根据流体网络模型计算得到单体冷却水流量分布，可以计算单体散热量。燃料电池主要通过冷却水与双极板对流换热来带走燃料电池产生的热量[18]，其带走的热量为：

式中，c为水的比热容，4.2 kJ/(kg·K)；m为水的质量流量，kg/s；∆T为水变化的温度，K。

基于燃料电池热阻模型，其中对于阴极催化层阳极侧存在下述热平衡方程：)

其中对于阴极催化层阴极侧存在下述热平衡方程：

式中，q1和q2分别为燃料电池单体阴极催化层两侧热流。

根据公式(17)～(21)相应的热阻以及产热和散热量对每块单体建立热平衡方程，通过求解热平衡方程组，即可得到每块电池的内部温度分布结果。

1.4 计算流程

通过上文可以得出，电池堆的温度分布将会影响单个电池的性能以及反应物的一些物性参数，而单体电池之间不同输出性能下产生的热量又会影响整个电池堆的温度分布，所以燃料电池堆模型是需要迭代计算的。将所建立的燃料电池模型在MATLAB中计算，其计算流程如图4所示。

图4 燃料电池模型计算流程图Fig.4 Fuel cell model calculation flowchart

（1）在初始计算中，输入氢气、空气、冷却水进口总流量和温度等运行参数以及歧管尺寸、单体数量等结构参数，并初始化燃料电池单体温度、氢气流量、空气流量和冷却液流量分布；

（2）根据单体温度、氢气流量、空气流量和冷却液流量分布，通过流体网络模型计算并更新每块电池的氢气流量、空气流量和冷却液流量分布；

（3）将单体的氢气流量、空气流量以及温度分布结果代入燃料电池电压模型，计算并更新每块电池的电压分布；

（4）根据燃料电池电压和冷却水流量分布，分别计算单体产热量和散热量，通过燃料电池热阻模型，计算并更新每块电池的温度分布；

（5）比较本次温度计算结果与上次温度结果的差值是否小于误差要求，如果大于误差，则将本次计算的温度分布代入步骤(2)中的流体网络模型重新进行计算；如果满足要求，则输出结果。

2 燃料电池模型仿真结果与试验验证

本试验对象选用某款110 kW 大功率燃料电池并基于开发的燃料电池热管理测试系统进行试验，燃料电池部分参数如表1所示。

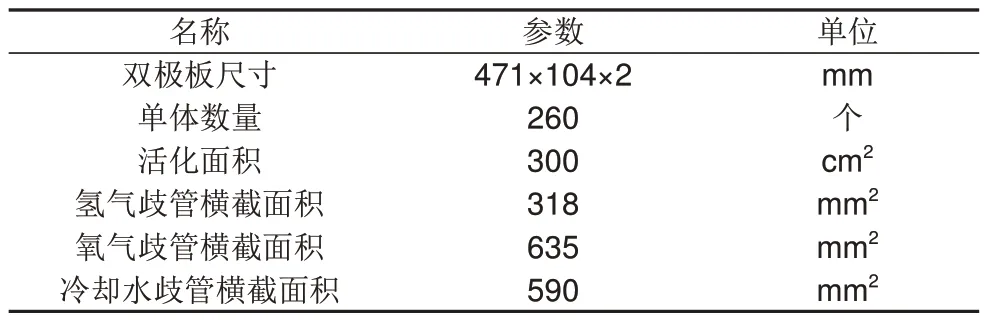
表1 燃料电池部分参数Table 1 Fuel cell partial parameters

根据GB/T 24554—2022《燃料电池发动机性能试验方法》，首先对燃料电池进行热机过程预处理，然后进行稳态特性试验，试验过程功率和工作电压随电流的变化和部分运行参数随电流的变化如图5所示。

图5 部分运行参数随电流的变化Fig.5 Variation of partial operating parameters with current

将图5所示的燃料电池相关运行参数代入所建立的燃料电池模型中，通过MATLAB进行计算，可以得到每块单体电池的气体流量、电压、温度等结果。由于在试验中单体电压和温度结果较气体流量方便获取，本工作将从试验中获得单体电压和温度进行仿真模型有效性验证。

其中不同电流下燃料电池单体平均电压的仿真与试验结果如图6所示，可以看出随着工作电流的增大，燃料电池单体平均电压减小，并且仿真和试验结果误差在3%以内。

图6 燃料电池单体平均电压的仿真和试验结果对比Fig.6 Comparison of simulated and experimental average voltage of fuel cell

按照离气体进口的距离从近到远对燃料电池单体进行编号。将试验台架记录的电池单体电压与仿真电压进行对比，结果如图7所示，燃料电池单体电压仿真与试验结果的误差在5%以内，证明了模型可靠性较高。同时随着工作电流的增大，燃料电池单体的电压变小，燃料电池单体电压的不一致性越来越明显，并且从整体上看，靠近气体进口侧的电压比远离气体进口侧的电压高，这符合“U 形”进气结构的特点，并且靠近燃料电池两端的单体电压会低于其他单体电压。

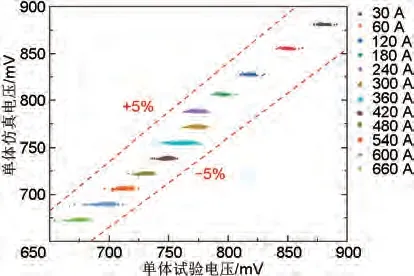
图7 不同工况下燃料电池单体仿真电压与试验电压对比Fig.7 Comparison of simulation and test voltage of fuel cell under different working conditions

在试验时，一般把冷却水出口位置的温度作为燃料电池堆的平均温度。将仿真计算得到的每块单体电池温度进行平均处理得到电池堆的平均温度，其结果如图8 所示，可以看出随着工作电流的增大，电池堆的平均温度也在增加，并且仿真平均温度和试验冷却水出口温度误差在2%以内。

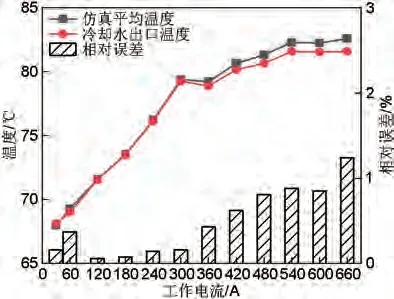
图8 燃料电池仿真平均温度和冷却水出口温度对比Fig.8 Comparison of fuel cell simulation average temperature and cooling water outlet temperature

同时通过试验测试平台配备的红外测温设备可以获得燃料电池工作时表面的温度数据。通过对获得的温度数据进行处理和修正，得到如图9所示的结果，绝大部分仿真误差在5%以内，证明了模型可靠性较高。同时从图中可以看出，燃料电池单体温度随着工作电流增大而增加，并且温度分布变得更不均匀，从整体上看靠近气体进口侧的温度比远离气体进口侧的温度高，并且靠近两端的单体温度要低于平均温度，同时工作电流较大时，两端单体温度会明显低于平均温度。这与单体电压的变化规律相似。

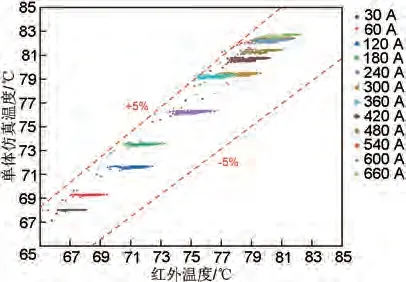
图9 不同工况下燃料电池单体仿真温度与红外温度对比Fig.9 Simulation and infrared temperature comparison of fuel cell monomer under different working conditions

3 运行参数对单体性能一致性的影响

从上述试验结果和仿真结果可以看出，燃料电池在工作时，单体性能存在不一致性，而在试验过程中电流变化的同时，冷却水温度与流量等参数也在发生变化。为更好地探究不同参数对燃料电池单体性能一致性的影响规律，本工作以660 A的试验工况（工作电流为660 A，冷却水流量为230 kg/min，冷却水进口温度为72 ℃）为基准，分别探究电流、冷却水流量和冷却水进口温度三个运行参数对单体性能一致性的影响。为使仿真更贴近实际使用情况，保证燃料电池工作在正常的温度区间（65～85 ℃），本工作探究的燃料电池工作电流为60～780 A，冷却水流量为120～420 kg/min，冷却水进口温度为50～80 ℃。

通过所建立的燃料电池模型进行仿真。由于燃料电池堆寿命取决于性能最差的单体，并且电压可以反映燃料电池的工作性能，所以有必要对单体电池电压最大值和最小值与平均值的偏离程度进行监测，本工作以电压最大偏差率SV来评价燃料电池单体的一致性，其中电压最大偏差率SV计算公式为[19]：

3.1 电流对单体电压一致性的影响

当电流作为唯一变量时，探究电流从60 A 到780 A 时燃料电池电压一致性的变化规律，其仿真结果如图10 所示。可以看出随着电流增大，燃料电池的电压减小，当燃料电池在较小的工作电流下时（300 A以下），单体电压一致性随着电流增大变化不明显，但是处于大工作电流下时（300 A 以上），单体电压一致性随着电流增大而变差，相较于300 A时，电流每增大10%，最大偏差率平均增大13%。

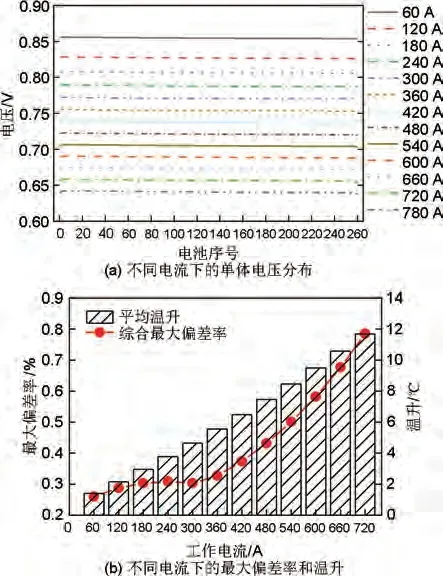
图10 电流为唯一变量的仿真结果Fig.10 Simulation results with current as the only variable

究其原因为当工作电流为唯一变量时，燃料电池单体散热基本不变，燃料电池堆的温度主要由产热决定，而产热跟工作电流有关，工作电流增加则会导致燃料电池的欧姆损失和活化损失增大，如图11 所示，可以得出欧姆损失和活化损失以及对应的极差均随着电流的增大而变大，但是欧姆损失的极差变化幅度随着电流的增大而增大，而活化损失的极差变化幅度随着电流的增大而减小，当工作电流从60 A 变化到300 A，欧姆损失极差增加了1 mV，活化损失极差增加了0.5 mV；当工作电流从300 A 变化到720 A，欧姆损失极差增加了5 mV，活化损失极差增加了0.3 mV。而欧姆损失主要在中等电流密度（0.15～1.2 A/cm2）下起作用，这也是导致当燃料电池在300 A电流以下时单体电压不一致性的变化幅度随着工作电流的增大而减小，在300 A电流以上时，单体电压不一致性的变化幅度随着工作电流的增大而增加的原因。因此单体电压的一致性将由欧姆损失和活化损失决定，同时工作电流对单体欧姆损失的影响较单体活化损失更大，因此这也使得燃料电池的工作性能一致性随工作电流的升高而降低。

图11 电流为唯一变量的欧姆和活化损失极差Fig.11 Ohmic and polarization loss polarization with current as the only variable

3.2 冷却水流量对单体电压一致性的影响

当冷却水流量作为唯一变量时，探究流量从120 kg/min到420 kg/min时燃料电池电压一致性的变化规律，其仿真结果如图12 所示。可以看出，随着冷却水流量增大，燃料电池的电压变小，单体电压一致性变好，相较于420 kg/min，流量每减少10%，最大偏差率平均增大8%。但是当流量增大到一定程度时，此时再增大流量对单体电压一致性改善不大。

图12 冷却水流量为唯一变量的仿真结果Fig.12 Simulation results with cooling water flow rate as the only variable

究其原因为当冷却水流量为唯一变量时，此时燃料电池产热一定，燃料电池堆的温度主要由散热决定，而散热主要与冷却水流量有关，呈反比关系。当流量大到一定程度时，对降低燃料电池的温升作用不明显，但是会额外增加泵的能耗。而单体温度的一致性则会影响单体电压的一致性，由于冷却水流量增大，燃料电池堆的温度降低，则会导致燃料电池的欧姆损失增大和活化损失增大，但是会使单体间温差变小，使得欧姆损失和活化损失的极差变小，如图13所示，当冷却水流量从120 kg/min变化到420 kg/min 时，欧姆损失极差降低6 mV，活化损失极差降低了1 mV，因此燃料电池工作性能的一致性随着冷却水流量增加而提高。因此在实际工作时，冷却水流量的选择应该结合工作电流、系统能耗以及燃料电池的工作温度区间进行确定。

图13 冷却水流量为唯一变量的欧姆和活化损失极差Fig.13 Ohmic and polarization loss extreme differences with cooling water flow rate as the only variable

3.3 冷却水进口温度对单体电压一致性的影响

当冷却水进口温度作为唯一变量时，探究温度从50 ℃到80 ℃时燃料电池电压一致性的变化规律，其仿真结果如图14 所示。随着冷却水进口温度增大，燃料电池的电压上升，虽然燃料电池的温升没有明显变化，但是单体电压一致性变好，相较于80 ℃，进口温度每减少10%，最大偏差率平均增大20%。

图14 冷却水进口温度为唯一变量的仿真结果Fig.14 Simulation results with cooling water inlet temperature as the only variable

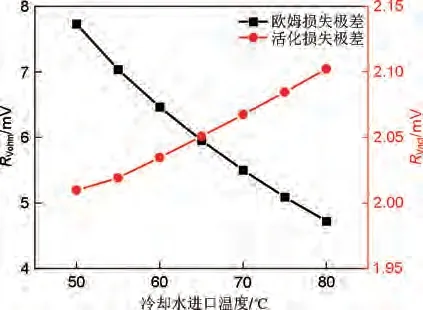
图15 冷却水进口温度为唯一变量的欧姆和活化损失极差Fig.15 Ohmic and polarization loss extreme differences with cooling water inlet temperature as the only variable

究其原因为当冷却水进口温度为唯一变量时，燃料电池堆的产热和散热基本不变，温升基本不变，因此冷却水进口温度将决定燃料电池堆稳定后的温度，这将会影响燃料电池的电压。随着冷却水进口温度降低，燃料电池堆的温度降低，燃料电池的欧姆损失和活化损失增大，当冷却水进口温度从50 ℃变化到80 ℃，欧姆损失极差降低3 mV，活化损失极差提高0.9 mV。所以单体工作性能不一致性将由欧姆损失和活化损失决定，虽然单体活化损失的一致性随着冷却水进口温度升高而降低，但是由于单体欧姆损失的一致性随着冷却水进口温度升高而提高，并且较单体活化损失，冷却水进口温度对欧姆损失的一致性影响更大，因此这也使得燃料电池工作性能一致性随冷却水进口温度升高而提高。虽然冷却水进口温度升高，可以改善单体性能以及提高其一致性，但是这会使燃料电池的工作温度过高，超过正常的工作温度区间，反而导致质子交换膜的破坏，进而使得燃料电池寿命减短。因此在实际工作时，冷却水进口温度应当合理选择，一般控制在65～70 ℃。