计及配网电压越限的光储协同优化运行策略

2024-04-02马洪艳

储能科学与技术 2024年3期

顾怡，邢洁，马洪艳，高杉

（东华大学信息科学与技术学院，上海 201620）

为推进实现我国“碳达峰”与“碳中和”的目标，新能源在电力系统中占比逐渐升高。光伏发电以其建设成本低与接入灵活的特点，成为中低压配电网中的主体电源之一[1]。根据中国电力企业联合会数据，2022 年分布式光伏的累计装机容量已达到157.62 GW，同比增长46.61%。随着配网侧光伏的持续接入，光伏出力与负荷的不平衡引发了电压越限问题[2]。一方面，过电压造成设备过热、影响绝缘，某些情况下甚至危及电网和人身的安全，限制了电网对新能源的接纳[3-4]；另一方面，低电压影响用户正常生活与生产，缩短设备运行寿命，增大了线路损耗[5]。

对分布式光伏引起的过电压问题，减小光伏有功出力是最直接的解决手段[6]，但却影响光伏消纳[7]。随着电力电子技术的发展，光伏逆变器调节无功参与电压控制的能力不断增强。文献[8]和文献[9]对光伏逆变器采用无功下垂控制调节配电网中的无功分布达到调压的目的，但受限于逆变器容量，调节能力不足时仍需对光伏有功进行削减，造成弃光。文献[10]和文献[11]提出了基于电压灵敏度的光伏逆变器控制策略，为所有并网逆变器分配无功补偿量以改善电压越限情况，但对于分布式光伏高比例接入的配电网仍需要光伏有功配合调节。此外，文献[12]通过调节变压器抽头位置改善电压分布，但有载变压器的分接头难以及时响应光伏出力变化，在一定程度上加大了实际应用的难度。对于光伏零出力的夜间低电压情况，往往采用无功补偿进行调节[13]。其中，电容器运行简单、组合灵活，但是无法平滑调节[14]，电力电子类调节设备如静止无功补偿装置补偿精度高，但不具备成本优势[15]。

上述治理电压越限的手段较为单一，难以适应复杂运行情况的变化，也不利于光伏消纳。近年来，储能系统凭借其调度灵活、安装方便的特点在配电网中得到广泛应用[16-17]，也有文献提出将其与光伏协调控制来治理电压越限问题[18]。

文献[19]和文献[20]基于分时电价，以光储投资维护、购售电成本等综合运行成本为目标，对储能电池和光伏容量进行配置，实现配电网的安全经济运行。文献[21]针对电力系统负荷峰谷差和光伏出力时间不一致的特点，利用分布式储能进行调节，用以提高光伏消纳，但是对于配网接纳光伏过程中是否存在电压越限情况没有进行进一步的考虑。文献[22]考虑将光储作为微网单元接入典型的配电网结构，建立了双层优化配置模型，对光储出力进行优化，但是该文献仅考虑了光储接入后对重负荷线路的低压改善，没有进一步分析低负荷情况下分布式能源对过压的影响。文献[23]和文献[24]研究了配电网中利用峰谷价差套利的储能系统调度策略，但是上述储能调度策略主要考虑的是削峰填谷带来的经济收益，没有进一步分析低储高发的运行方式有可能会进一步加剧电压越限，即白天光伏出力高峰区域同样也是储能装置放电套利区间，此时储能放电不但进一步造成了电压越限，也影响了光伏消纳；晚间某些工况下的储能充电也会加剧低压现象。

同时考虑过压和低压联合治理的相关研究还不太丰富。文献[25]采用电气距离对配电网进行集群划分，并根据不同集群的电压越上、下限严重程度对分布式储能有功进行电压调节比例分配，但该研究未进一步考虑储能的安装运行成本。文献[26]将逆变器无功利用率与储能系统荷电状态变化量作为一致性变量，通过其光-储联合调节解决电压越限问题，但仅分析了光储的调节成本，未考虑配电网的综合运行费用。

基于此，本工作提出了一种计及配电网电压越限的两阶段光储系统协同运行的优化调度策略，在保证配网安全运行的前提下，考虑了光储接入配电网的综合运行成本。该策略综合考虑光伏无功调节与储能有功充放电对配电网电压越限进行治理，策略的第一阶段根据可调光储节点数，确定投入的储能节点与有功出力，以及光伏无功可调节点；第二阶段建立了光储运行优化模型。该模型以储能的调度成本、购售电成本以及网损成本之和最小为目标，考虑了网络运行和设备容量等约束，通过粒子群算法对模型进行求解，得到光储系统日调度出力。以北方地区的实际配电网为算例，验证了本工作方法的有效性和可行性。

1 分布式光伏对配电网电压的影响

分布式光伏接入配网后会影响原系统的潮流大小和方向，馈线上的电压分布将由原来的单调下降变为可能存在局部极大值，从而导致部分接入点产生过压。图1为接入分布式光伏的配电网馈线示意图。设线路上有N个用户，第n个用户的负荷为Pn+jQn(n=1，2，…，N)。当n=1 时，线路阻抗为R1+jX1；当n≥2 时，线路上第n-1 个用户和第n个用户之间的线路阻抗为Rn+jXn=ln(r+jx)，ln为两个相邻用户之间的线路长度，r和x分别为单位长度线路的电阻和电抗。节点p接入的分布式光伏出力为SPV=PV+jQV。

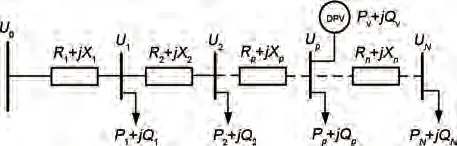
图1 分布式光伏接入配电网馈线示意图Fig.1 Distribution feeders diagram of distributed photovoltaic connected

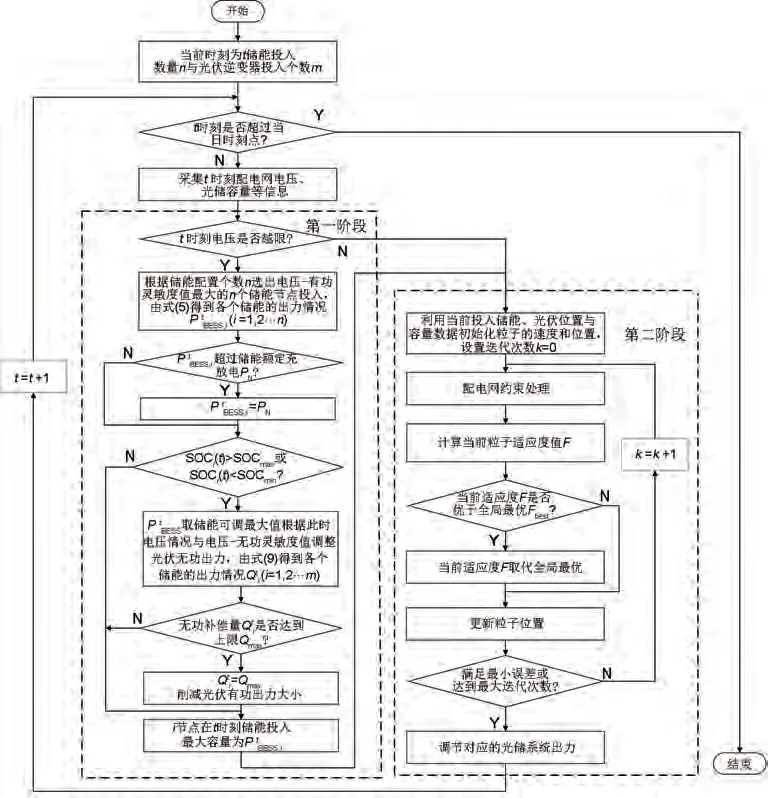
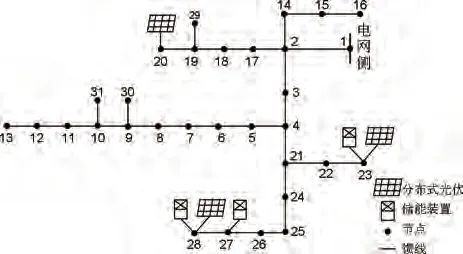
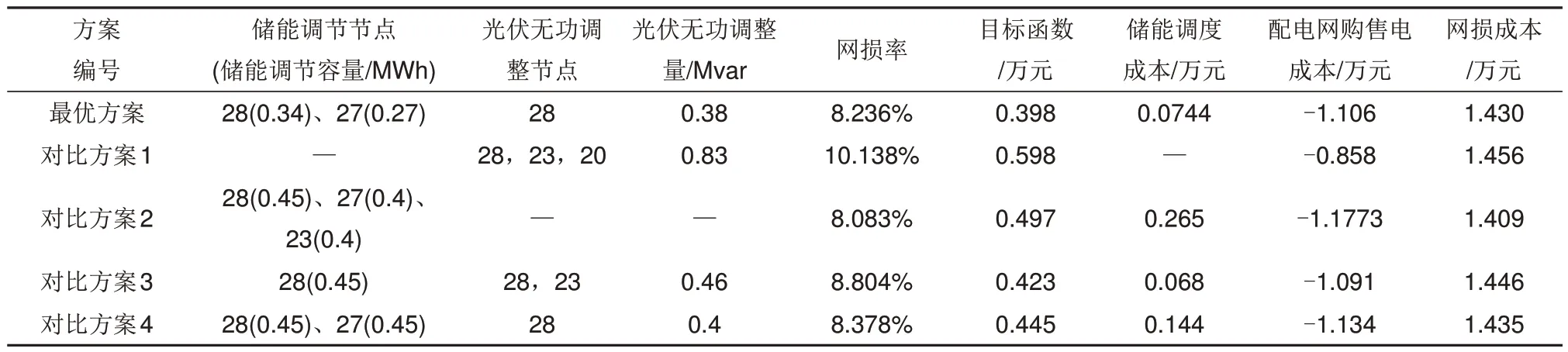
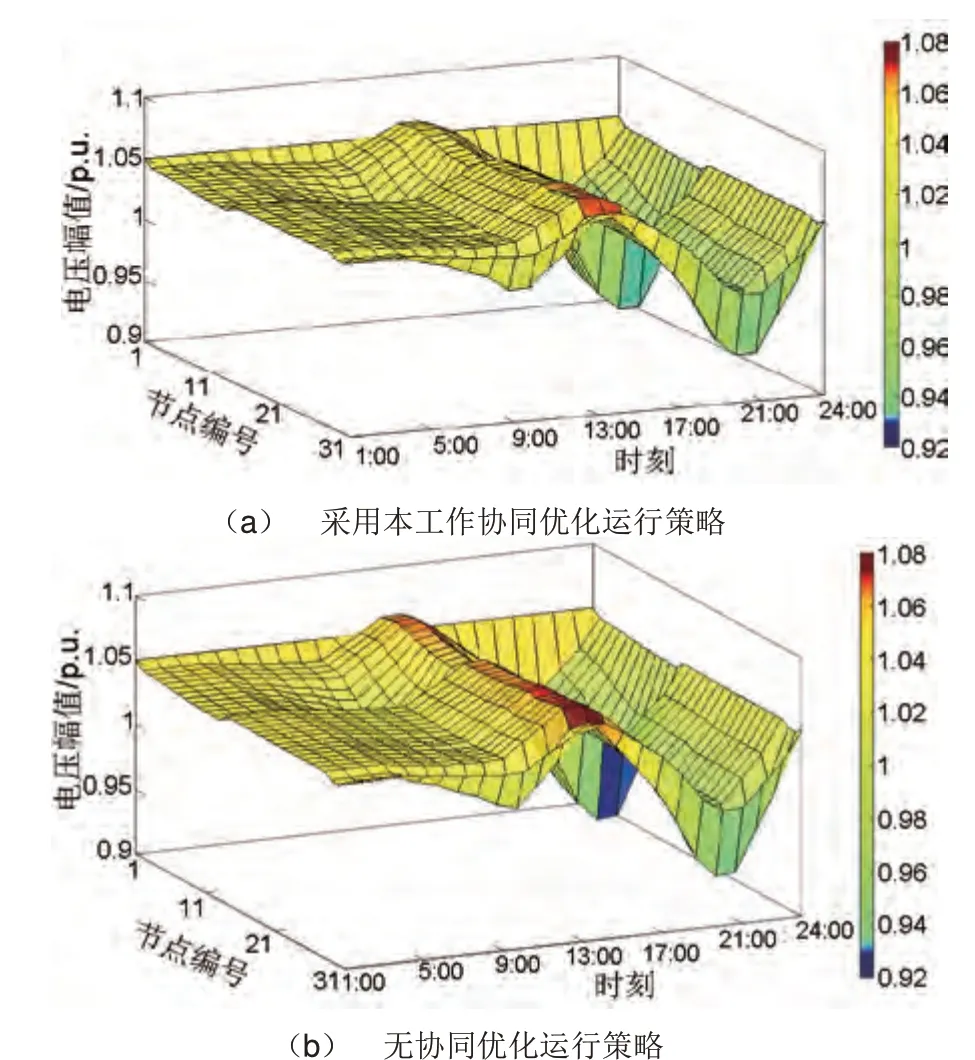
若线路初始端电压为U0，对于位于光伏接入点前的用户m(0

因用户消耗的通常为阻感性负荷，因此负载有功Pn和负载无功Qn均大于0，相较于分布式光伏接入前，m点电压升高。

位于光伏接入点后的用户j(p

由式(2)中可以看出j点电压也会升高，是由于分布式光伏的接入使p点电压Up有所抬高，而节点p后的电压降落值没有发生变化，因此使光伏接入点后的节点电压也一起升高。

当夜间分布式光伏不出力时，则式(1)中PV和QV均为0，且馈线末端节点的Rn与Xn值较大，末端节点电压可能会出现低压情况，影响正常供电。

分布式光伏接入配电网后，其有功功率和无功功率的波动均会对电压产生较大的影响，不同节点功率的改变对电压的影响可以通过电压灵敏度因数(voltage stability factor，VSF)来反映，其描述了节点注入的有功或无功功率对网络特定位置电压变化的影响程度，可通过雅可比矩阵求逆得到[27]，如式(3)所示。

式中，Δδ和ΔU分别表示电压相角和幅值变化量，ΔP和ΔQ分别表示有功功率和无功功率变化量，SPδ、SQδ、SPU、SQU为雅可比逆矩阵的分块矩阵。对于已配置n个含调节有功进行变压的设备，m个含调节无功进行变压的设备的系统，其i点电压幅值变化量ΔUi受有功变化量ΔPn和无功变化量ΔQm的影响为：

式中，SPU(i，j)为电压-有功灵敏度因数，表示节点j注入(或吸收)有功功率对节点i电压幅值的影响，数值越大，则电压抬升(降低)效果越明显；SQU(i，j)为电压-无功灵敏度因数，表示点j注入(或吸收)无功功率对节点i电压幅值的影响。

2 光储联合运行的电压越限治理策略

为了解决分布式光伏和负荷不平衡引起的节点电压越限问题，并且提高配电网安全运行下的经济效益，提出了光储系统协同调节的两阶段策略。该策略的第一阶段中，针对电压越限的时刻，计算各光储节点的电压-有功/无功灵敏度并进行排序，根据此时光储装置可调节点的个数，确定可调节光储节点及储能出力初值。策略的第二阶段中，建立光储联合运行优化调度模型，以配电网运行成本最低为目标，基于当前配电网光储容量信息或阶段一中给出的光储调节节点与储能出力范围对模型求解，优化每个时刻的可调储能与光伏出力，得到配电网最优运行成本。两阶段光储协同优化运行策略如图2所示。

图2 两阶段光储协同优化运行策略示意图Fig.2 Diagram of two-stage optimization operation strategy of DPVs and ESSs

2.1 阶段一：确定光储可调位置与储能出力范围

在阶段一中以治理电压越限为目的，根据可调光储系统的个数和额定充放电功率限制，确定可调储能节点与出力范围，同时调节光伏逆变器进行电压治理。该阶段的具体步骤如下。

步骤1：根据电压灵敏度系数确定储能的调节节点与有功出力的初值。若系统中有N个节点安装储能，其中有n(0≤n≤N)个可调储能节点，当节点i在t时刻出现电压越限时，对各个节点j的电压-有功灵敏度SPU(i，j)进行排序，前n个数值最大的储能可调节点投入，该时刻n个可调储能的有功功率调节量ΔP=[ΔP1, ΔP2, …, ΔPn]T。

为合理分配各个储能的有功调节量，引入有功贡献度系数kp[22]，则对于n个储能装置有功调节量为：

在仅考虑有功的调节量时，可将式(4)改写为：

式中，ρi为0-1 变量，若节点i接有储能系统，且与配电网存在功率可调时，ρi=1，否则ρi=0。由式(3)求得电压灵敏度后，且已知电压调节量ΔUi，可结合式(6)，求得贡献度系数kp值为：

已知系数kp值后，可根据式(5)得到储能有功调节量ΔP。

步骤2：当储能的荷电状态SOC已达边界或达到最大的额定充放电功率PN，此时节点电压仍越限，则考虑光伏无功调节量。调节量计算同步骤1，引入无功贡献度系数kq，根据电压-无功灵敏度矩阵SQU，在储能装置作用后，电压调整量更新为ΔUi´，式(4)可改写为：

式中，ΔQ=[ΔQ1,ΔQ2, …, ΔQm]T；γj为0-1 变量，若节点j接有光伏系统，且与配电网存在功率可调时，γj=1，否则γj=0。

步骤3：在光伏逆变器达到设定的功率因数极限值后，此时需要削减有功出力，同步骤1，在储能装置与光伏无功出力共同作用下缩减光伏有功。

2.2 阶段二：优化储能与光伏出力

阶段二以经济运行为主要目的，利用阶段一中计算得到的可调储能节点与出力值，以及光伏调节节点，以配电网运行成本最小为目标，优化储能出力与光伏出力。阶段二中构建的光储协同运行优化模型如下。

2.2.1 目标函数

式中，CBESS为储能装置的调度成本；CGrid为配电网中的购售电成本；CLoss为网损成本。

（1）储能装置调度成本

综合考虑储能系统的一次配置投资成本与运维成本[28]，储能的调度成本计算公式为：

式中，KBESS为储能系统的单位调度成本；Pdisn,h(t)和Pchn,h(t)分别表示第n个储能装置在h时段的放电和充电功率；η为储能系统的充放电效率。

（2）购售电成本

光伏就地消纳，剩余电量进行上网，同时储能装置对负荷的峰谷进行调节，并根据运行状态进行低储高发套利。配电网中购售电成本为：

式中，Pi和Qi分别为注入节点i的有功和无功功率；Ui和Uj分别为节点i和j的电压幅值；j∈i表示所有与节点i直接相连的节点；Gij和Bij分别是节点导纳矩阵的实部和虚部；θij是节点i和j之间的相角差。

（2）节点电压约束

式中，Umin和Umax分别为节点i电压幅值的下限和上限。

（3）最大交换功率约束

为确保电网和光伏系统稳定安全运行，对电网和光伏系统间的交换功率容量有所限制，即

（4）储能系统约束

储能装置的荷电状态SOC 在时序上具有连续性的特征，按照单位时间的充放电功率的大小进行累计计算，在一个运行周期内，储能装置的SOC满足下式：

式中，SSOC,max和SSOC,min分别为荷电状态的上、下限。

蓄电池充放电功率约束为：

式中，PBESS,in(t)和PBESS,out(t)分别为蓄电池充电功率和放电功率；PBESS,in,max和PBESS,out,max分别为蓄电池充、放电功率限值。

（5）光伏逆变器可调无功容量

光伏逆变器为电网提供无功功率支撑，此时光伏逆变器的无功可调容量Q可表示为：

式中，S为光伏逆变器的视在功率，P为光伏在该时刻输出的有功功率。

3 算法流程

在电力系统经济运行的研究中，粒子群算法凭借鲁棒性好、收敛速度较快的优点应用广泛。本工作第二阶段的优化模型采用嵌入式潮流粒子群算法[29]进行求解，利用阶段一中得到的光储出力范围生成粒子，迭代调节网络中的控制变量，根据网络更新后的电压与网损状态等信息，对配电网运行成本进行计算，得到储能装置与光伏在24 h内的出力情况。具体优化步骤如下：

①输入配电网光伏与负荷当前时刻出力，以当前储能装置、光伏的容量范围作为粒子的求解空间。

②初始化粒子群算法参数：根据储能可调个数与光伏调整个数配置空间维数D，初始化粒子群的位置与速度，种群规模取N，迭代次数取k，起始值k=0，惯性权重为ω，学习因子为c1和c2。

③对每个粒子进行适应度F计算，将每个粒子的适应度与全局最优Fbest进行比较，更新最优个体Pbest与全局最优值gbest。

④更新粒子群位置与速度，k=k+1，直到满足最小误差或达到最大迭代值后，结束寻优，输出结果；否则返回步骤③。

两阶段策略的具体流程如图3所示。在该策略的第一阶段中，针对电压越限时刻，计算电压-有功/无功灵敏度确定可调光储节点，并通过储能当前时刻的荷电状态SOC 与额定充放电功率PN，确定储能最大出力；在该策略的第二阶段中，根据当前时刻光储可调节点与容量等信息通过粒子群算法求解光储运行优化模型，光储按照优化结果调节出力，进入下一时刻的优化运行。

图3 两阶段方法总流程Fig.3 Flow chart of two-stage method

4 算例仿真及结果分析

本工作以河北某郊区10 kV配电网为例进行分析，该配网拓扑结构如图4所示。节点1为电网侧，节点23、27 和28 安装了储能系统，节点20、23和28 安装了分布式光伏，光伏总有功出力峰值为12 MW，总负荷有功峰值为10.40 MW，负荷功率因数为0.85～0.9。典型日各光伏和负荷出力曲线如附录图1所示。

图4 31节点配电网网络结构Fig.4 31-node distribution network structure

储能设备参数见附表1，其中KBESS计算参考文献[22]。该地区分时电价见附表2，光伏上网价格为0.42 元/kWh。根据国家标准GB/T 12325—2008：10 kV供电允许偏差为±7%，本工作选取节点电压上、下限分别为Umax=1.07 p.u.，Umin=0.93 p.u.。

表1 不同对比方案下光储运行结果Table 1 The operation results of PVs and ESSs in different contrast schemes

针对如上算例，采用本工作所提出的策略进行电压越限治理与优化运行，参数设置：粒子群种群大小为N=500，迭代次数取k=100，惯性权重ω=0.8，学习因子c1和c2均为2。最优配电网运行方案中调节配电网中已投入的节点28和节点27储能装置，在已有的光伏装置中，调整28 节点光伏无功出力，优化结果如表1第一行所示。

为了进一步验证本工作策略方法的有效性，改变光储可调个数，可得其他优化结果，见表1中的对比方案。其中，对比方案1无可调储能节点，仅光伏可调；对比方案2仅储能系统可调，光伏不可调；对比方案3 中考虑单个储能可调，光伏可调；对比方案4中储能光伏均可调节，但仅采取阶段一中对电压越限的治理，未考虑阶段二的优化。

通过分析各方案可见，对比方案1不考虑储能的调节，只调节分布式光伏，与其他含储能调节的方案相比，其光伏无功调整量最大，网损率最高，且总经济成本的目标函数在各方案中最高。其余方案都考虑了不同数量与不同容量的储能的调节，配电网网损率明显降低，最优方案相较于对比方案1减少了490 kW 有功损耗。此外，考虑储能系统的调节也可以降低弃光率、减少向上级电网的购电成本并且可以通过低储高发套利，进一步降低了购电经济成本，达到了总成本的最优。

对比方案2仅采用储能装置进行治理，未调节光伏。结果表明，虽然该方案网损率最低，但是由于储能调节量过大，调度成本较高，达到0.265万元，相较于光储联调的最优方案经济性较差。

对比方案3相较于最优方案，减少了可调储能节点的数目，虽然在储能调度成本上有所减少，但增加了网损，且在储能套利收益上不占优势，增大了配电网购电成本。

对比方案4相较于最优方案，未采用策略中的阶段二模型对光储出力进行优化，在储能调度成本、购售电成本和网损成本上都高于最优方案，尤其是在储能调度成本上，相较于最优方案成本接近提升一倍，该对比方案目标函数高于最优方案0.047万元。

图5为本工作最优方案对应的典型日的光伏出力、负荷出力、储能出力以及光伏无功出力曲线，其中储能功率为正代表充电，储能功率为负代表放电，光伏无功为正代表吸收无功功率。其中在典型日中储能系统有两次充放电循环，一次是在光伏出力最大，负荷出力较小时充电抑制过电压现象，在夜晚低电压时放电；另一次是在夜晚电价低时进行充电，在上午用电高峰期且电价较高时释放。光伏出力用于本地负荷，多余功率上网。在23 点至次日5 点为用电低谷，此时蓄电池从电网购电充能，为用电高峰时备用，6:00—11:00 为一日内首个用电高峰期，蓄电池输出功率；12:00—15:00为用电低谷时期，存在过压现象，储能进行充电，20:00—21:00 达到用电高峰，储能输出电能，进行低电压治理，提升用户电能质量，后续的22:00—24:00，若储能蓄电池仍有剩余电量，则继续向系统供电，若没有剩余，也不从电网购电。该过程实现了光伏能量的转移，减少了光伏资源浪费，有效降低配电网网损，提高电能质量。

图5 配电网24 h出力曲线Fig.5 Power curves of distribution network in 24 hours

图6(a)展示了采用本工作策略后配电网一天内的实际电压变化，由图可见电压最高处通过光储协调治理未超过限值1.07 p.u.，电压最低处的时间段内也通过储能放电，将电压保持在正常范围内。按照各时刻的采样数据，复现无治理情况下的配电网24节点的电压变化情况，如图6(b)所示，深红色区域内表示在13:00—14:00内，节点27、节点28发生电压越上限的情况，过压接近10%；在深蓝色区域内表示在20:00—21:00，节点13 出现了低电压现象，电压幅值为0.926 p.u.。综上可见，本工作策略通过对光储协同控制，能有效解决配网过电压与低电压问题。

图6 配电网24 h节点电压Fig.6 Node voltage in 24 hours

5 结论

本工作针对目前大量分布式光伏接入配电网引起的电压越限问题，综合考虑电网中的光储调节手段，提出了一种两阶段光储优化运行策略，在治理电压越限的同时，通过光储的联合调度优化了配电网的经济运行。

该两阶段光储优化运行策略的阶段一以治理电压越限为目标，确定光储投入节点位置与储能系统出力范围；阶段二建立了以配电网运行成本最小为目标的运行优化模型，采用粒子群优化算法对模型进行求解，得到了光储的日实时调度策略。

通过河北某郊区实际10 kV配电网为算例，验证了本工作所提出的策略方法的有效性。此外，讨论了单独的光伏调节、单独储能充放以及光储联合作用的不同效果。结果表明：在考虑原有的光伏运行基础上，通过储能系统的灵活调节可以有效对电压越限现象进行治理，尽管储能装置的调节会产生一定调度成本，但是其带来了一定的售电收益，并增加了光伏消纳。当光伏和储能可调数量改变时，该两阶段策略也能有效改善配电网的运行情况。

附录