液流电池堆分析与计算程序

2024-04-02李晓蒙李京浩张谨奕

储能科学与技术 2024年3期

李昂，李晓蒙，李京浩，张谨奕

（国家电投北京和瑞储能科技有限公司，北京 102209）

新型储能设施作为电力系统的补充设备，更是清洁能源有效利用的关键一环。主要的技术路线包括电化学储能(锂电池、铅酸、铅炭、全钒、铁铬、锌铁等)、电磁储能(电容、超导等)和物理储能(抽水蓄能、压缩空气、飞轮储能等)。截至2022 年底，抽水蓄能和锂电储能占累计装机容量的97.5%，中美欧占全球投运容量的80%。“十四五”期间，中国计划建设的非抽水蓄能的新型储能设施为64 GW。2022 年，储能进入发展的快车道，特别是液流电池同比增长近338%[1]。依靠数值仿真和有限元软件等工具，以及工程化项目的验证，液流电池的降本与产品迭代正在加快。中外公开的论文及文献涉及了液流电池的数值仿真及建模，内容涵盖流量与系统控制[2]，电池结构的紧凑化设计与性能优化[3]，电极性质参数对电池性能的影响[4]，以及电池堆的流道设计与旁路电流的平衡[5]等。以上论文偏向控制、材料和反应机理的研究，而电池本体设计需要统筹考虑电性能、流体阻力、密封和热管理等方面。上海交通大学团队基于MATLAB Simulink，建立的全钒液流电池模型包含了电化学模型、流阻计算模型和系统热力学模型[6]。美国麻省理工团队创建了一款一维线性代数的GUI界面软件，应用于一种刻流道双极板的全钒单电池的数值仿真。计算包括旁路电流和流体阻力，并仿真了反应机理，模拟出电池的充放电性能曲线[7]。基于降低参与设计人员的技术门槛，快速获得概念设计电池的部分性质参数，开发了这款界面运行的软件。内部四个主页面分别计算电池堆内的电流分布、流体阻力、集装箱内的稳态散热，以及电池结构的密封压力和螺杆选型。

1 电池堆旁路电流

液流电池堆板框的流道内和外接管路内的电解液是导体，堆内电极区反应产生的电流可以通过板框表面的流道和外接管路流失，最终以热的形式扩散进环境，降低电池堆的库仑效率。因此，需要计算板框流道和电池外接管路的电阻。

通过减小流道截面积和增加流道的长度能增加电阻，降低旁路电流，但会增加流阻。另一种方式是在满足电池电压的前提下，将大电池堆拆分成电池节数较少的分堆，再将分堆的电路串联，同步调整出入液管道尺寸，液路总管将电解液输送进被分隔板隔开的分堆控制电流损失[8]。将电池堆液路等效成电路图进行分析的研究较为广泛，例如在MATLAB Simulink 界面拖拽电阻、导线、电压源、电流源、安培表等模块建立等效电路图。若电池堆的电池单元不多，逐个修正模块参数和拖拽较为便捷。运行输出的线图的横坐标为运行时间，纵坐标为安培数。此方式仅体现出电池堆内有旁路电流的累积，不体现每节电池的实际情况。

当需要计算的电池单元数持续增加，流道和外接管路的尺寸进行迭代优化时，模块化编程的效率低下和失效体现在：①重复修正嵌入模块的内置参数，并机械性地复制粘贴出所需模块；②反复拖住导线，并连接大量模块形成电路；③运行出的线图数据需要从Simulink 界面导出成Excel 形式，再导入MATLAB进行数据分析。由于电流数值不对应电池节，并不能分析出堆内实际的电流分布和趋势线；④电路计算原理未知；⑤Simulink 运算时间较长。

因此，需要从电路分析原理出发，列举出函数计算公式，并以此建立电路的运算矩阵，才能全面反映出电池单元的数量、分堆个数、流道设计尺寸与堆内旁路电流分布间的关系，从而开展迭代设计。文献中展示出的计算方式是基于KVL、KAL和节点法将M节电池的等效电路梳理出5M-2个线性方程进行求解[9-10]。此方式对于单堆构型的计算较为便利，但较难应用于多分堆构型的等效电流图求解。流道内电解液阻值Rn的计算如公式(1)所示。其中，σE代表电解液的电导率，Ln代表流道长度，An代表流道截面积。

1.1 电流损失计算原理

KVL结合网格法分析电路的计算方法，通用于单堆和多分堆构型的电池。相较于节点法可以大幅减小线性方程的数量，避开KAL参与等式配平，减少未知电流的求解个数。

图1所示的等效电路图是一个包含了20节电池的电池堆，被平均分隔成了4个分堆的构型。每片分隔板的侧壁有入液口和出液口，均通过总管进行电解液的分配和回流。每个分堆有一对集流铜板，4 个串联分堆的集流铜板用导线按照正负极顺序连接。流道与管路内的电解液是有电阻的导体，图中R2、R3、R4、R5分别代表了板框表面的限流通道、板框表面的共享通道、每个分堆进出液管道和连接分堆的总管的电阻。Re代表每节电池材料的内阻，U0是每节电池的电压，It是电池堆的充放电电流。

图1 多分堆电池四分之一简化电路图Fig.1 Equivalent quarter circuit of a simplified multiple sub-stack battery

液流电池是对称设计，限流通道入液侧的电阻和出液侧的电阻是并联关系。因此，电路中的R2、R3、R4、R5均为实际值的一半，由此简化出二分之一等效电路图。由于液流电池的正极与负极侧的设计相同，图1所示的四分之一等效电路图可以理解为电池堆的正极入液侧。

电池堆的电流循环用网格电流i20表示，代表电源电流It逐次通过每节电池的内阻，且每节电池是独立的电压源。图中，主电流一部分进入电极区参与电化学反应，另一部分通过限流通道流失进电解液的液路循环，造成库仑损失。将图1中的等效电路图，按照网格法分析形成KVL等式。图中每一个箭头代表一个电路循环，总计20 个。Mesh 20 是电池堆的外接电源，其KVL方程用i20=It表示。以下是Mesh 1～Mesh 10的KVL等式：

通过以上计算，可以获得等效电路图中i1～i10的循环电流。循环电流由于流动方向的不同，经过加减后得到每个电阻的实际通过电流。电池堆内，通过Re的电流是每节电池的实际通过电流。通过R2的电流是每片板框流道内的旁路电流。汇总后通过R3的电流是逐节电池旁路电流在公共通道内的积累。

图2 用于对比在相同的管路与流道设计条件下，将一个整电池堆分隔出不同数量的分堆可以有效控制堆内的旁路电流。假设一个有120节电池的电池堆被分隔板均分成2、3、4、6 个分电池堆，每个分电池堆有独立的出入液接管，但从总管进行电解液的分配和回流。按照仿真设定的参数观察，四种方案旁路电流值从大到小依次是2 分堆、6 分堆、3 分堆和4 分堆。图2 数值计算的旁路电流分布证明，并非液流电池的分堆数越多，漏失的电量就越少。综合考虑装配难度和原料成本，3 分堆最优。

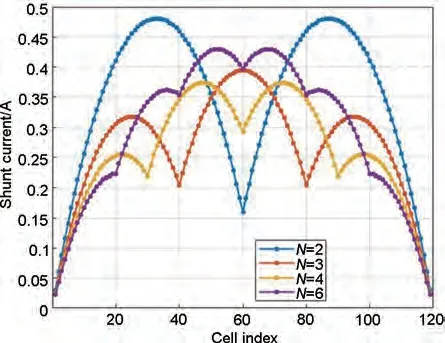
图2 多分堆内旁路电流分布Fig.2 Shunt current distribution in multiple substack batteries

1.2 电流损失计算示例

图3所示的是电池堆机械设计因素造成的旁路电流的计算界面。运行前需要填写的输入参数存在默认值，不修改按照表1中的默认值运行。需要设定的参数如下：①选择电解液体系，自动确认系统默认的电池标准电势和充放电区间；②电解液条件；③恒流充放电的电流密度；④电极的宽度和长度；⑤电池堆的分堆个数和每个分堆内的电池节数。

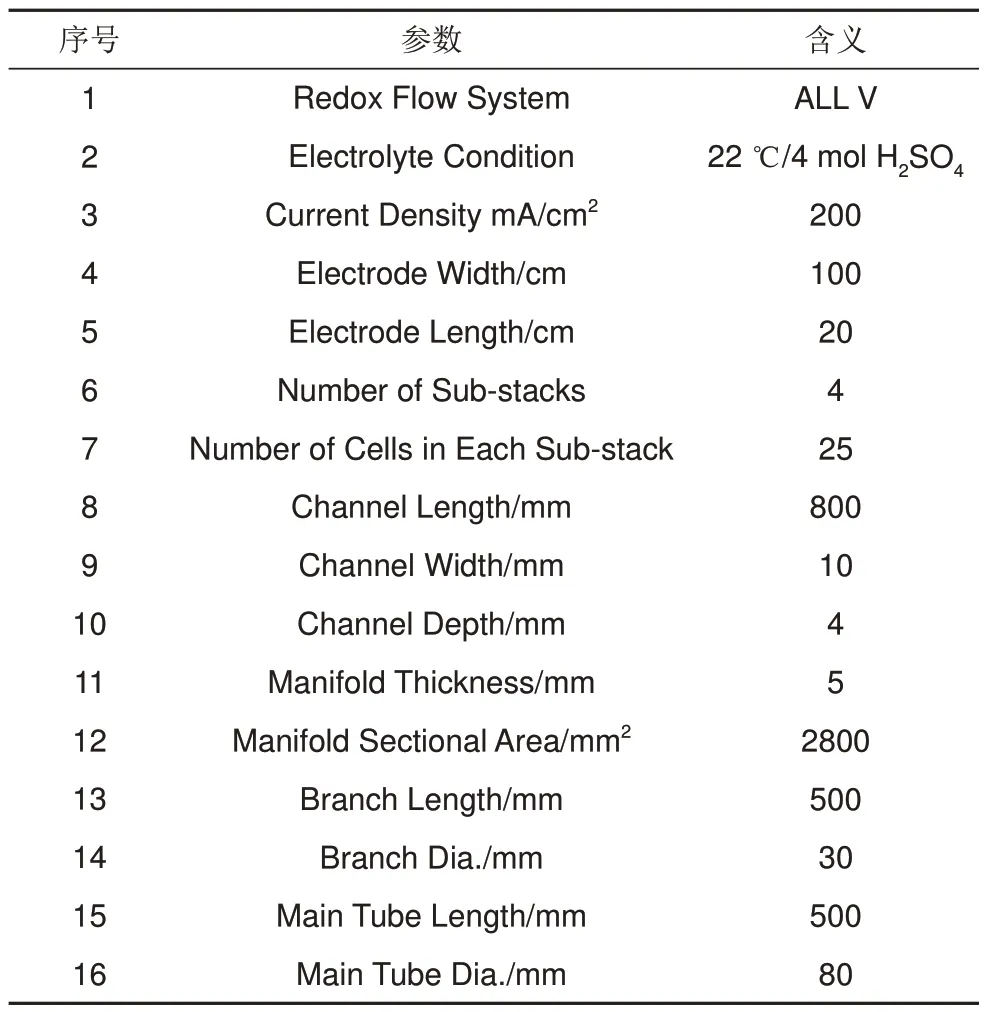
表1 电池堆内电流分布运行主要参数Table 1 Input properties of computing a stack interior current distribution

图3 电池堆内电流分布计算界面Fig.3 Operation interface of a stack interior current distribution

电池堆内的旁路电流由液流框表面流道和电池堆的外接管路共同控制，在电池堆板框和管路设计栏中，需要输入流道和管路的几何尺寸。顺着电解液流动方向的电极边长为长度方向。运算输出的参数包含：电池堆需要的恒流充放电电流的大小、电池堆的额定功率、恒流充放电时共享通道内汇集的最大漏电量、相对应的库仑效率损失率、损失的功率、电池流道框表面流道和电池堆管路在选择的电解液电导率下的电阻值，以及电池单元的电阻值。

电池堆内电流分布计算的逻辑概述如下：输入计算参数，确定电解液的种类、电流密度、电极尺寸、电池堆分堆个数和电池节数、板框表面主要流道尺寸和主要管路的尺寸。根据网格法和KVL公式分析电池堆的等效电路图，并建立相应的计算矩阵函数，运算出充电时刻和放电时刻每个电池单元的网格电流。再根据网格电流的走向进行加减，求解出每节电池的实际通过电流、板框表面限流通道内的电流、电池堆内逐节电池共享通道内积攒的漏电流。

图4中逐节电池的电流数值和电池堆内电流的分布图均根据表1的输入参数进行计算。电池堆在200 mA/cm2恒流充电条件下，电池堆的接入电流为500 A，电池堆的额定功率为55.2 kW。电池堆是4分堆，共享通道内的最大积攒漏电在充电时是4.466 A，放电时是4.301 A。机械设计造成的堆体库仑损失约1.213%，功率损失是669.6 W。液流电池每片板框限流通道的电阻是370.4 Ω，共享通道是0.02646 Ω。电池堆每段出入液管电阻是13.1 Ω，汇总管段的电阻是1.842 Ω。每节电池的材料内阻约0.5 mΩ。

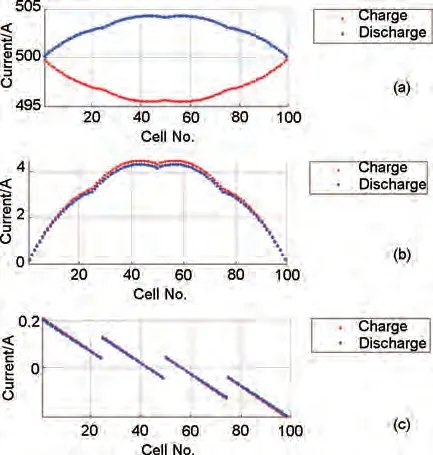
图4 (a)电池堆逐节电池的实际通过电流；(b)共享通道内累计的电流；(c)流道框表面流道内的电流Fig.4 (a)Real current flow through each cell; (b)shunt current accumulated in stack manifold; (c)shunt current in frame channel of each cell

2 电池堆流体阻力

液流电池堆板框的流道和外接管路，既是控制堆内电流损失的电阻，又是电解液进行液路循环并参与化学反应的通道。流体阻力与流动速度呈平方关系，泵的损耗降低系统效率。因此，流道设计基于低流体阻力和高电阻效应，两者负相关，需要通过计算找到泵损和库仑损失的平衡点。电极是流体阻力的主要来源，影响因子是电极的渗透率和单位流量。通过软件计算，可以获得在设定参数条件下电极、流道、外接管路和堆体静压力的流阻值，以及各因素占比。

2.1 流阻计算原理

流体阻力计算基于达西定律，由主阻力降∆Pmajor和局部阻力降∆Pminor构成。雷诺数判断电解液的流动状态，代入Churchill达西摩擦系数计算公式，用于求解电池堆出入液管的主阻力降，参见公式(2)～(6)。此法涵盖了层流、过渡流和湍流三种流动状态[5]。圆管内阻力降的计算存在误差，层流状态的计算误差约40%，湍流状态的计算误差约15%[11]。

2.1.1 矩形流道阻力

板框矩形流道的主阻力计算所用的达西摩擦系数是实验拟合的经验公式(8)，并代入公式(9)计算矩形流道的有效水利直径，计算相应的雷诺数。之后，再代入Churchill 达西摩擦系数公式(3)，通过公式(6)求解矩形管内的主阻力降[12]。矩形管路内的平均流速计算参见公式(11)，与流量Q、流道宽度Wn和流道深度Hn相关。

若公式(10)计算出的矩形流道内的雷诺数小于2300，则板框流道内的电解液处于层流状态，主流阻力降的计算结果很准确。若雷诺数是大于4000 的湍流，计算误差约10%。由于线性方程计算精度低，无法考虑板框流道内更多的细节影响，统一将计算值扩大10%[11]。

2.1.2 局部阻力降

板框表面流道主要由90°和180°弯头构成，流道出口一般为T字形通道，局部阻力系数Kminor可以用3K 法较为准确地计算。公式(13)中的K1、K∞、Kd均为3K 法常数，通过查表确定。fminor表示一段流道的局部阻力系数之和[13]。

2.1.3 电极阻力降

电解液经过电极的阻力降ΔPe主要由电解液黏度μ、多孔电极渗透率Ke和流经长度Le影响。We为电极幅宽。电极造成的压降是顺着电解液的流动方向，与电池堆内电极的个数无关，电极厚度He和孔隙率决定了电化学反应空间。假设每节电池分配到的流量相同，u⇀是电解液在电极流经方向的速度张量，等效为流经电极内的平均流速[14]。

2.2 流阻计算示例

图5所示的是电池堆流道设计造成的流体阻力计算界面。运行前需要填写的输入参数存在默认值，不修改按照默认值运行，参见表2中的数值。电极尺寸与厚度、单位面积流量和与之相乘的流量系数，决定每节电池的额定流量。电极阻力的影响因子是电极渗透率和电解液温度，这是因为电解液的黏度与运行温度相关。虽然存在电极渗透率的经验计算公式，但计算结果与实际测量值有较大偏差。所以，界面内需要人工输入实际测量的渗透率，取消了计算式需要代入的碳丝直径和卡曼-柯兹尼常数。

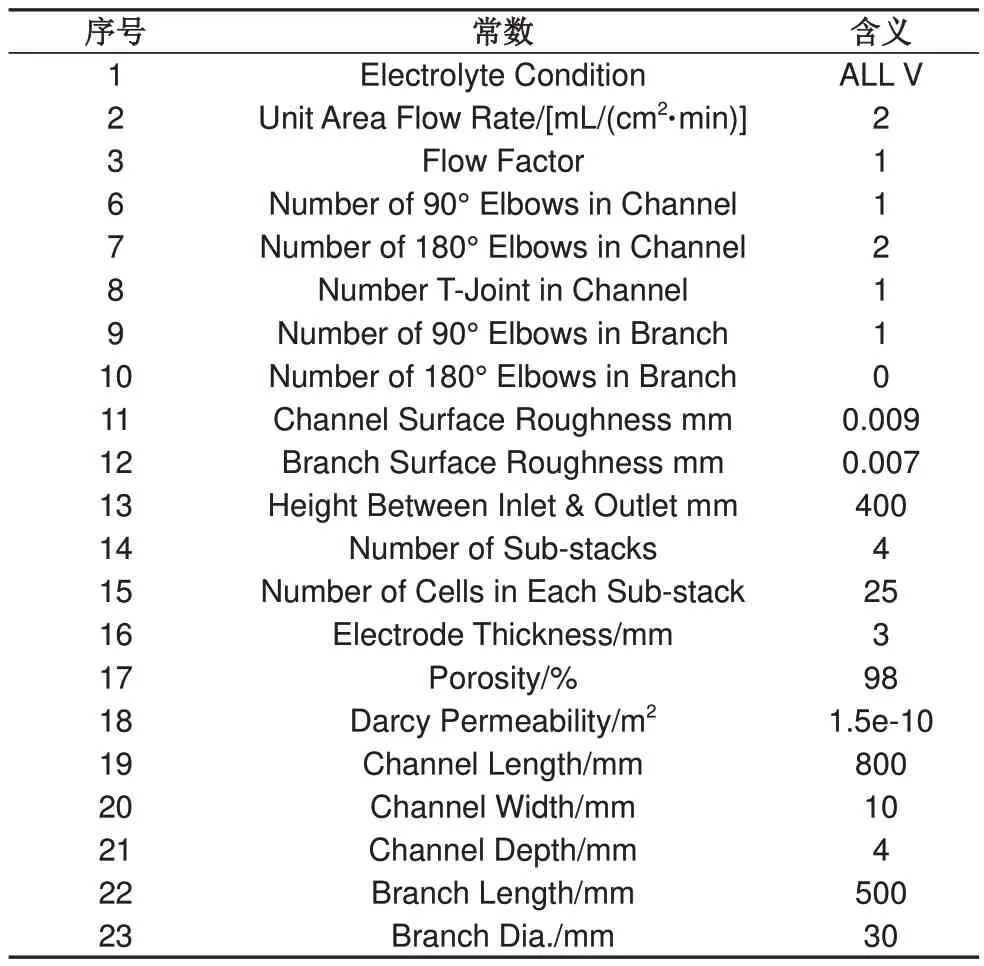
表2 电池堆流阻运行主要参数Table 2 Input properties of stack flow resistance computation

图5 电池堆流体阻力计算界面Fig.5 Operation interface of a stack flow resistance computation

电池堆内流体阻力的计算逻辑概述如下：输入计算参数，确定电极孔隙率、渗透率、外形尺寸。确定板框表面流道的一系列尺寸、电池堆分堆个数和电池节数。电极阻力降计算通过电极孔隙率和渗透率公式结合流量进行求解；液流框表面限流通道截面积为矩形，根据矩形流道的经验公式，结合达西定律、电池节流量，求解出主阻力降；液流框表面限流通道的局部阻力降求解代入“3K”法中的常数、电池节流量，求解出局部阻力降；电池堆出入液管路的流体阻力计算流程与限流通道相同，但根据圆管公式求解主阻力降、局部阻力降；求解电池堆进出入管高度差造成的静态压强；绘制饼图，体现电池堆内不同流体阻力贡献的占比。

图6 是电池堆内流体阻力的贡献占比，源自图5 界面，根据表2 的参数进行运行的结果。其中电极占比59%，板框流道占比34%，电池堆出入液管占比6%，出入液管间高度差造成的静压占比1%。根据表2 的输入参数计算，每节电池的流量是4 L/min，每个堆正极或者负极的总流量需求是400 L/min。电极内的平均流速是2.268 cm/s，板框流道内的平均流速为1.6667 m/s，电池堆出入液管内的平均流速为2.358 m/s。电池堆总的流体阻力是125.8 kPa。其中，电极的阻力降是74.07 kPa，流道总阻力降42.35 kPa，出入液管总阻力降7.814 kPa，静压是1.57 kPa。

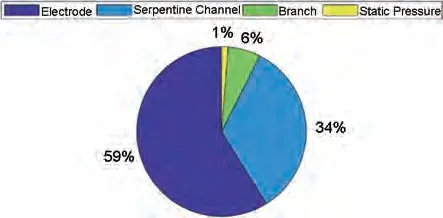
图6 流体阻力各因素占比Fig.6 Proportion of various factors in flow resistance

3 电池堆散热

液流电池加热器能耗是系统功率损耗的另一主要来源。电池的热管理系统关系到加热器、泵、储罐和电池堆。加热器维持储罐内的电解液温度，储罐和系统的管路布置涉及散热和保温计算。电池堆本体既涉及散热和保温，又涉及充放电过程中的反应热计算。反应热产生量与参与电化学反应的离子浓度、堆内电解液体积和泵的功率相关[15]。系统稳态运行条件时泵匀速运转，通过调控加热器让堆内的温度基本恒定。电池堆的外形尺寸、外表面的保温层厚度及其传热系数决定了电池堆在稳态运行时的散热量。液流电池堆一般放置在厂房或者集装箱内运行。由于堆体表面温度高于环境，边界层散热由温差造成的浮力驱动，热力运动方向与重力方向相反。运行程序将电池堆体简化成四类表面：端板面、上表面、下表面和侧面，并覆盖保温层。自然对流散热进行以下假设：①电池堆处于稳态；②材料性质参数为常数；③忽略不同材料交界面的接触热阻；④等效的热学模型仅从表面散热，材料厚度方向无热量散失。通过程序可以计算出电池堆在不同环境温度和堆内温度的条件下，堆体无保温和有保温时的散热量。

3.1 散热计算原理

电池堆内的温度高于环境温度，热量散失顺序是内部的热量穿过腔体，扩散进入环境中。固体间热传递为导热，分成单层材料和复合层两种。单层材料的导热位于电池堆的侧面和上下表面，计算式参见公式(16)。要考虑复合层的情况：端板侧、端板侧添加保温层，以及电池堆上表面添加保温层。重叠材料间存在接触热阻，假设接触热阻很小，则接触热阻两侧的温度一样。复合层的导热系数是将每层材料的热阻等效成串联电路，参见公式(17)。电池体被拆分成四种存在厚度的面模型，假设热量仅沿着平行于厚度的方向传递，厚度法向的传递为零。其中，As代表散热表面的面积，Ts代表散热表面温度，R代表多层材料的串联热阻。每种材料的导热系数、厚度和散热表面积分别用K、L和A表示，并用下角标进行区分。

自然对流是因为表面边界层与环境存在温差，这使空气产生了密度梯度，结合重力场产生的浮力推动了热量散失。自然对流的散热量Qconv受温差以及跟空气的接触面积影响，参见公式(18)。第三种热传递Qrad通过电磁波，无需传递介质存在。不同材料的辐射系数介于0～1，取决于材料本身性质、表面粗糙度和外形。热辐射的量与温度呈四次方关系，参见公式(19)。通过材料导热出的能量Qcond等于其表面传热和热辐射的散失量之和[16]。

图7所示的是自然对流计算流程。计算的第一步是根据公式(21)，用假设的表面温度计算边界层的平均温度。之后查表3，确定在标准大气压下干燥空气的性质参数。若温度值不能准确对应表格中的值，可以通过插值法估算出特定温度下的参数值。假设空气是理想气体，公式(23)计算的瑞利数被定义为浮力和黏性力之比，与动量和热扩散系数之比的乘积。用于描述热量传递的形式是热传导，或超过临界值(RaL≈109)的对流传热的无量纲常数。引入努塞尔数为代表的经验公式(24)方便工程计算，评估平均自然对流系数hˉ。

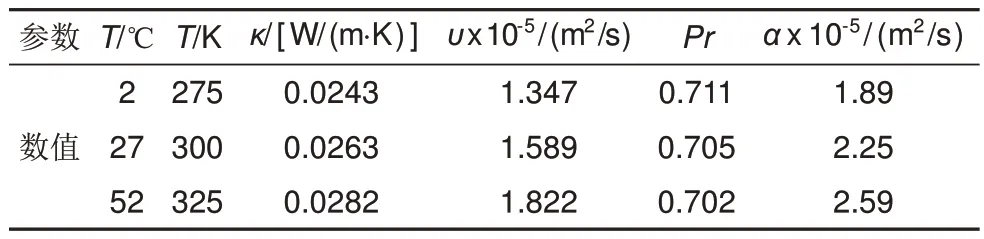
表3 标准大气压干燥空气迁移性质参数[18]Table 3 Transport properties of dry air

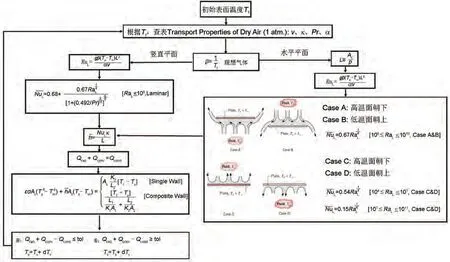
图7 自然对流散热计算流程Fig.7 Flow Chart of heat loss calculation by free convection

因为自然对流是浮力驱动，散失方向与重力相反。水平平面和竖直平面的散热被分成两类模型，而水平平面散热被进一步分解成四种情况：①物体下表面温度高，环境温度低(Case A)；②物体上表面温度低，环境温度高(Case B)；③物体上表面温度高，环境温度低(Case C)；④物体下表面温度低，环境温度高(Case D)。竖直平面无论表面温度高于或低于环境温度，均采用一种模型。

3.1.1 水平平面

水平平面热量散失模型应用于电池堆的上下表面的计算。由于电池堆表面温度高于环境，上表面按照Case C模型计算，下表面按照Case A模型计算。在运用公式(23)计算瑞丽数时，需要代入的特征长度用公式(25)计算，含义如同流体中的水利直径，即整个矩形面为热量散失的通路，其中常数p代表散热表面周长。为进一步确定自然对流的导热系数，需要根据瑞丽数判断是哪一种水平散热，参见公式(26)～(28)努塞尔数的计算。

3.1.2 竖直平面

竖直平面热量散失的计算流程与水平平面相同，但特征长度的定义是沿着热量散失方向的矩形表面的边长。电池堆侧面和端板面的特征长度为矩形面的短边长。因为电池堆表面温度跟环境相差不大，不会出现湍流一类的高强度对流，层流热传导用公式(29)计算得更准确[17]。

3.1.3 表面温度迭代计算

计算平均自然对流系数hˉ，需要代入努塞尔数——-NuL和干燥空气的导热系数κ。热量从堆内散失到空气的过程遵循能量守恒，即堆内导热出的热量跟表面通过对流和热辐射散失的总和相同。

按照图7中的流程计算，若通过表面散失量与材料导热量之差低于容差，初始设定的表面温度降低dTs，重复之前的运行进行一次迭代计算。若表面散失量与材料导热量之差高于容差，初始设定的表面温度增加dTs，重复之前的运行进行一次迭代计算。直至导入材料的热量与散失热量达到平衡，终止迭代，输出此面的表面温度、热辐射量及传热量。

3.2 散热计算示例

图8所示的是电池堆稳态自然对流散热的计算界面。运行前需要填写的输入参数存在默认值，不修改按照默认值运行。需要设定参数包括电池节数、绝缘板片数。电池堆的高度与宽度、端板的高度与宽度，如界面中的电池堆示意图所示，并且标明了电池体各面的位置。电池堆本体的保温性由内部液体距离堆体表面的距离决定。因此，还需要输入电池堆侧面的壁厚、顶面/底面壁厚，以及两端绝缘板的厚度。程序默认堆体的两个侧面、顶面和底面覆盖保温层的厚度相同，两个端板面的保温层厚度相同，均要在参数设定页面内输入厚度值。程序默认绝缘板的导热系数为聚丙烯、电池堆端板导热系数为钢、保温层导热系数为聚氨酯。程序默认集装箱内干燥空气的温度区间为2～52 ℃，并规定了相关空气计算的参数值。程序默认电池堆表面温度为10 ℃。

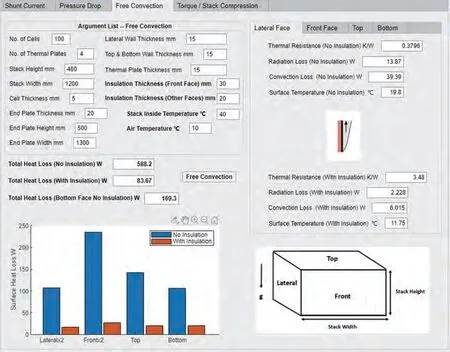
图8 电池堆散热计算界面Fig.8 Operation interface of stack free convection computation

运算输出被分进四个页面，按照电池堆的侧面、正面、顶面、底面体现。每个界面内求解出了表面在无保温和有保温两种条件下，材料的热阻值、热辐射散热量、传热散热量和表面温度。总散热量的累加结果分成无保温、全保温、除底面外的五面保温，进行情况输出。

图9是电池堆六个面在有保温和无保温条件下的散热量，源自图8根据表4的输入参数进行运算，电池堆在10 ℃的集装箱内，堆内温度稳定在40 ℃。如图9 所示，两个侧面无保温的散热量为106.5 W，两个端板面的散热量为234.1 W，堆体上表面的散热量为142.2 W，堆体下表面的散热量为105.3 W，无保温电池堆的总散热量是588.2 W。假设端板面覆盖的聚氨酯厚30 mm，电池堆其余表面覆盖的聚氨酯厚20 mm，全保温的散热量是83.67 W。一般电池堆的底面无保温，此时总散热量为168.3 W。

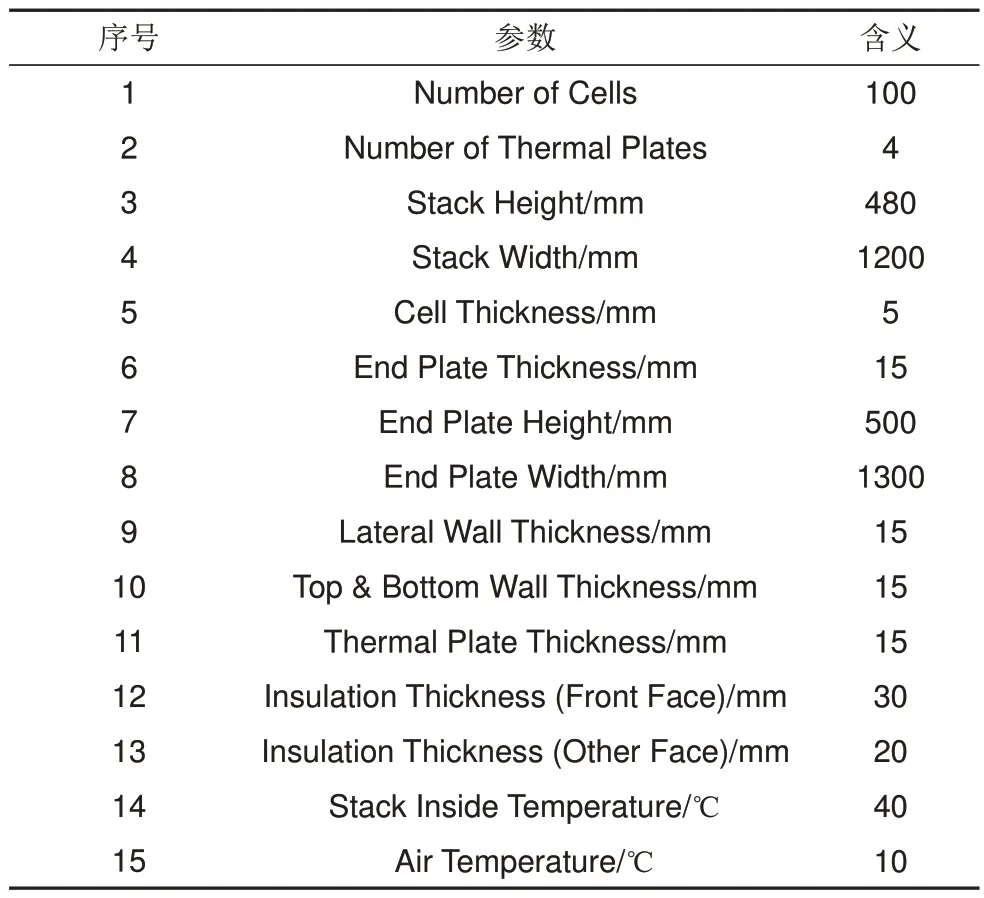
表4 自然对流散热运行主要参数Table 4 Input properties of computing free convection heat loss

图9 电池堆各表面散热量(有保温和无保温)Fig.9 Heat dissipation from stack surfaces (with insulation & no insulation)

按照四种表面分类。电池堆侧面无保温时，材料热阻是0.3796 K/W，热辐射量13.87 W，传热量39.39 W，表面温度19.8℃。使用20 mm厚聚氨酯进行保温，含保温层的材料热阻约3.48 K/W，热辐射量2.228 W，传热量6.015 W，保温层表面温度11.75 ℃。

电池堆端板无保温时，材料热阻是0.1772 K/W，热辐射量27.67 W，传热量89.41 W，表面温度19.25 ℃。使用20 mm厚聚氨酯进行保温，含保温层的材料热阻约2.101 K/W，热辐射量3.86 W，传热量9.665 W，保温层表面温度11.3 ℃。

电池堆上表面无保温时，材料热阻是0.1518 K/W，热辐射量29.15 W，传热量113.1 W，表面温度18.35 ℃。使用20 mm厚聚氨酯进行保温，含保温层的材料热阻约1.392 K/W，热辐射量3.833 W，传热量16.64 W，保温层表面温度11.25 ℃。

电池堆下表面无保温时，材料热阻是0.1518 K/W，热辐射量50.41 W，传热量54.9 W，表面温度24 ℃。使用20 mm 厚聚氨酯进行保温，含保温层的材料热阻约1.392 K/W，热辐射量8.755 W，传热量10.9 W，保温层表面温度12.75 ℃。

4 电池堆封装压力与螺杆选型

液流电池用一定数量的螺杆和弹簧等效压力机的封装力进行密封。提前计算的目是避免错误的螺杆选型造成密封失效，或者过度设计增加成本。计算原理是将电池堆的零件等效成串联或者并联的一维线性弹簧，用胡可定律求解。封装压力用于将堆体翘曲的板框找平、将板框表面的密封垫压入密封槽、电池运行时内部液体的压力、抵消热态运行时的膨胀[19]。常规型号的紧固件是强度8.8级的M10、M12、M16 和M18 的粗牙螺杆，选前需要校核安全扭矩上线，避免每根螺杆等效的轴向力扭矩接近警戒值Tmax，或者设计赘余。螺栓强度计算过程如公式(31)～(33)所示[20]。

图10 是通过电池堆简化模型确定的封装压力和选型螺杆数量。运行前需要填写的输入参数存在默认值，不修改按照默认值运行。界面可以计算的单电池结构是板框加内嵌盖板的形式，在三个分页内分别填入：电池各种材料的杨氏模量和密度、主要零件的表面积与厚度，以及材料热膨胀系数和一些关键的计算参数，如板框片数、密封槽深度、液流框翘曲量、弹簧刚度、电池堆内液体压力、电极尺寸以及环境温差。

图10 电池堆封装压力计算和螺杆选型界面Fig.10 Operation interface of stack compression computation & stud selection

根据等效刚度模型，计算出无螺杆电池堆的刚度与电池节数间的关系。根据密封垫凸出密封槽的量、找平板框翘曲两项估算出的电池堆下压量，结合电池堆的刚度系数，求解出电池堆的最小封装压力。由于热胀冷缩，求解出抵消材料热膨胀需要额外施加的力。根据堆内液体压力和电极表面积，求解出抵消液体压强需要的力。总封装压力为螺杆预紧力的输入参数，按照二选一选择螺杆。一列是备选螺杆的型号和根数，另一列是使用螺杆的型号和根数。人工用扭矩扳手施力的最大误差约25%。

根据材料强度和螺杆小径，求解出螺杆的可承受的最大扭矩。由螺杆中经、螺牙尺寸和接触面摩擦力，计算出在总封装压力下的螺杆扭矩。需要判断螺杆的安全扭矩和等效封装力的实际扭矩的大小。若最大扭矩小于实际扭矩需求，说明需要增加螺杆数量或者选用更粗的螺杆。若最大扭矩大于实际扭矩需求，可以维持选型，或者减少螺杆个数或者选用更细的螺杆。运算输出数值是电池堆总的封装压力，并且细化出找平板框翘曲、压平密封垫、抵消堆内液体压力、电池热胀冷缩各项需要的力值。

图11 表示电池堆封装压力各因素占比，源自图10 的输入参数进行计算。堆体刚度是随着电池节数的增加呈对函数递减。电池总封装压力为23.11 T（1 T=10000 N）。其中，找平每片板框2 mm的翘曲需要13.62 T，占比59%。将2 mm厚密封垫压入1.5 mm 深密封槽需要3.614 T，占比16%。电池堆内部的液体压力预计200 kPa，需要4.077 T 的力防止运行过程中泄漏，占比18%。假设电池堆在集装箱内最大经历20℃的温度变化，堆体需要施加1.802 T 的力防止螺杆因为材料收缩而松弛，占比8%。电池堆不含螺杆和紧固件的重量约525.6 kg。

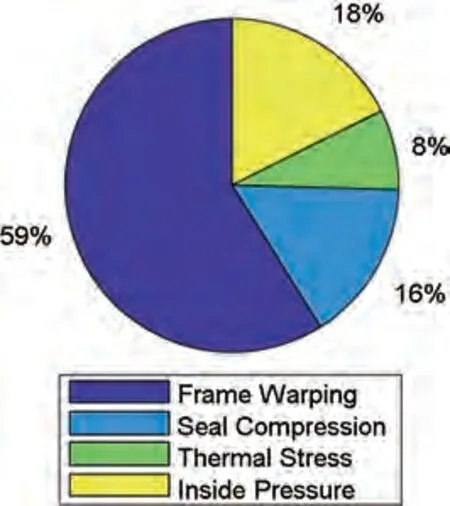
图11 影响电池堆封装压力各因素占比Fig.11 Proportion of influence factors in stack compression force

图12 是电池堆螺杆选型计算，两种备选螺杆是M10 x 1.5和M12 x 1.75，均使用16根，假设人工预紧的扭矩误差为12%，等效出每根M12 螺杆的预紧扭矩为37 Nm，材料安全上线约74 Nm，施力余量过多。可以维持杆数量，保证施力均匀的基础上，选细一个型号。若选用M10 螺杆需要进行31 Nm的预紧，材料安全上限约42 Nm，满足应用条件。

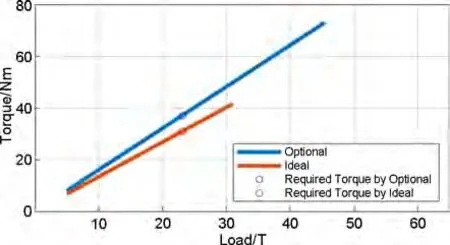
图12 螺杆选型Fig.12 Stud selections

5 结论

液流电池堆的机械设计需要通盘考虑流道结构、体积优化、封装压力、保温等方面。某一个设计参数或者特征尺寸会影响多个指标参数。创建GUI软件的目的是让研发人员快速获得产品的部分性能进行方案对比，加快设计迭代。将多学科物理模型和软件代码封装成可视化界面，降低了电池设计工程师的技术准入门槛，有利于研发人员独立验证方案，并对液流电池建立全方位了解。

符号说明

An、A1、As——流道横截面积、螺杆小径截面积、散热表面的表面积

Dh、Deff——水利直径、矩形流道有效水利直径

d、d1——螺栓中经、螺杆小径

fd、fRe、fminor、F0——达西摩擦系数、矩形流道达西摩擦系数、总局部阻力系数、螺杆拉伸力

h¯、He、Hn——平均自然对流系数、流道深度、电极厚度

i、It——网格电流、外接电流

KAL、KVL、K、Ke、Kminor——基尔霍夫电压定律、基尔霍夫电流定律、材料导热系数、电极渗透率、局部阻力系数

L、Le、Ln——散热表面特征长度、电极长度、流道长度

P、ΔPe、∆Pmajor、∆Pminor——散热表面周长、电极流体阻力、流道主阻力降、流道局部阻力降

Q、Qrad、Qconv、Qcond——电池单元流量、热辐射功率、传热功率、导热功率

R、Re、RaL、Rn、Re、R2、R3、R4、R5——复合层材料导热阻、雷诺数、瑞利数、流道内电解液内阻、电池单元内阻、板框限流通道内阻、板框共享通道内阻、电池堆出液液支管内阻、电池堆出入液汇总管内阻