基于损失特征矩阵的CHB-BESS模块间接地故障诊断

刘志豪，高逸群，张 君，凌志斌，李旭光

（上海交通大学，上海 200240）

储能系统是智能电网的重要组成部分，应用于削峰填谷、提高输变电设备利用率、新能源接入等场景；电池储能系统常见的功率变换系统(power conversion system，PCS)为模块化多电平变换器(modular multilevel converter，MMC)与H 桥级联型 变 换 器(cascaded H bridge converter，CHB)，其中CHB-BESS 拓扑结构和控制逻辑简单，得到了广泛的应用[1]。随着电池储能系统的电压等级提高和体积增大，CHB-BESS 模块间接地故障的发生风险逐渐增大，尽早检测和定位故障对于避免其他部位的二次伤害，减少系统的经济损失至关重要[2]。目前，CHB-BESS 模块间接地故障诊断的相关研究尚处早期。

对于储能系统的接地短路故障，阈值方法可用于判断储能系统的直流线路短路故障的发生[3-4]，但不适合故障定位的复杂需求；注入法可用于实现功率变换器外部交直流线路接地故障的故障定位[5-6]，但是一般适用于长输电线路。而对于PCS 内部故障，目前的研究成果主要是功率开关、电容等器件的开路或短路故障[7]。在功率器件开路故障等内部故障诊断方面，基于数学模型的诊断方法研究成果丰富[8-12]。其中，对于CHB 与MMC 等多子模块结构PCS 的功率器件开路故障定位，一般是遍历子模块进行估算或测量[13-16]。

基于模型的方法，通过建立状态估计模型来评估过程量或者状态量等参量的偏差，完成故障诊断和定位，诊断原理清晰，是电力电子系统故障诊断的常见方法[17]。开关函数模型可描述不同功率开关开路故障时的电气量变化[18]。对于并网中性点钳位逆变器系统，以Concordia电流模型描述电流随故障位置改变的变化，提供了直接计算故障状态的方法[19]。基于单相CHB变换器的状态估计模型，从部分已知状态量，估计出直流链路电压等系统状态量，将其与实测状态量对比，实现开关开路故障定位[20]。对使用模型预测控制(model predictive control，MPC)的MMC，利用预测模型计算结果与实测信号的偏差，实现故障诊断，减少了额外的计算需求[21]。其中，基于状态估测模型或者MPC 等估算模型的方法，实时计算对比状态量或者过程量并用于故障诊断。

模块间接地故障的故障特征主要体现在零序电流上[2]。然而，由于接地过渡电阻变化范围较大，即使故障发生在同一位置，零序电流也会呈现显著的变动[2]。基于模型的定位方法要求相对准确的电阻值，以计算零序电流，在过渡电阻不确定的情况下，无法获得可信的零序电流计算结果。故障接地电阻的不确定性使得相对准确的解析模型难以获取，无法通过基于解析数学模型的方法来实现PCS内部接地故障的定位。因此，相对于功率器件开路等PCS 内部器件故障，故障接地电阻的不确定性成为影响PCS 内部接地故障定位的主要因素。对故障接地电阻变化的鲁棒性成为CHB-BESS 模块间接地故障定位的主要挑战。

为实现计及接地过渡电阻不确定性的快速鲁棒诊断，本工作提出一种基于损失特征矩阵的故障定位方法。该方法同时对故障位置和过渡电阻进行遍历并计算零序电流。当故障位置和过渡电阻与实际情况最接近时，计算结果与测量结果的偏差最小，可作为故障定位的依据。此外，为降低遍历计算的开销，本工作采用梯度下降优化算法进行加速。

首先，本工作建立了零序等效电路模型；然后，将零序电流模型离散化，提出基于损失特征矩阵的定位方法，并证实故障定位问题作为最优化问题具有最优解唯一性，最优解可作为接地过渡电阻不确定情况下的可靠定位结果；接着，提出最优计算方法实现加速诊断。最后，结合实验结果进行分析，验证方法的有效性。

1 CHB-BESS模块间接地故障

CHB-BESS的模块间接地故障示意图如图1(a)所示，其主要由CHB-BESS及其滤波电感、线路、网侧电源组成。对于CHB-BESS 的模块间接地故障，基频等低频特征与等效开关频率等高频特征均为重要的故障特征，因此选取π型等效电路作为网侧线路等效模型[2]。其中，Lf为滤波电感；L1、R1、C0、Lm、Rm为线路π型等效电路的参数。

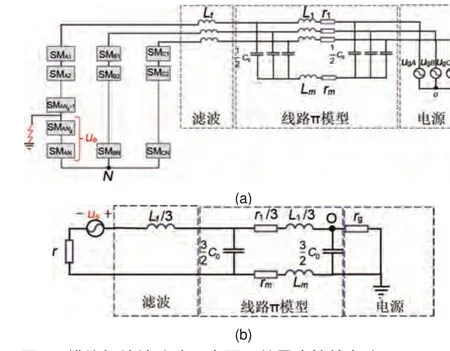
图1 模块间接地故障示意图及其零序等效电路：(a) CHBBESS模块间接地故障示意图；(b) 零序等效电路Fig.1 Schematic diagram of (a) ground fault between modules and (b) zero sequence equivalent circuit

CHB-BESS 模块间接地故障的故障特征主要呈现在零序成分上，这是因为功率控制算法会控制正序功率成分[2]。由图1(a)可得，零序等效电路如图1(b)所示。其中，ue为零序等效电源电压；r为接地过渡电阻；rg为电源中性点接地电阻。

零序等效电源ue为故障相接地侧子模块输出电压的叠加，含有故障位置信息。

式中，uSM,i为子模块电压；n为接地位置。

网侧等效阻抗为

式中，rg为网侧接地电阻；Xc0= 2jω3C0为对地容抗；X1=r1+jωL13 为线路阻抗；Xm=rm+jωLm为地阻抗；Xf=(rf+jωLf) 3为滤波阻抗。

对于高电压大容量的CHB-BESS，对地零序电压不易测取[22]，零序电流可作为故障诊断及故障定位的主要电气量特征。

式中，I为零序电流；Ue为等效电源电压，是零序电流所含故障位置信息的来源；r为故障接地过渡电阻，会引起零序电流的显著变动。

2 故障定位

2.1 离散化计算模型

鉴于零序电流计算对基频与开关频率均有需求，使用Tustin 算法得到式(3)的离散化计算形式[23-24]，用来计算零序电流。

式中，ap、bq为与Zeq、r和采样间隔相关的系数；îm为m时刻的零序电流计算值；ue,m为m时刻的等效电源电压。

对每个采样时刻，使用子模块的驱动控制信号和直流电压来描述零序等效电源电压，得到式(1)的离散化形式，即为式(4)中的等效电源电压。

式中，Udc为直流侧电压；si为子模块的开关状态，对于单极性倍频调制有+1、-1、0 三种状态。

2.2 基于损失特征矩阵的故障定位方法

定义拓扑矩阵M来描述故障位置与过渡电阻的遍历参数。

式中，ni是故障位置；rj是故障接地电阻；N为单相桥臂子模块数量，即故障位置维度的离散化数量；Nr为接地过渡电阻维度的离散化数量。

对于拓扑矩阵M任一元素，计算该接地位置和过渡电阻条件下的零序电流，并得到相较于实测结果的偏差。本工作选用平均绝对误差(mean absolute error，MAE)，即L1损失，来描述偏差。

式中，im为m时刻的零序电流测量值；Nc为零序电流采样序列及计算序列的长度。

定义损失特征矩阵L来描述不同条件下的偏差。

由式(6)与式(8)可知，基于一个拓扑矩阵M可计算得到相应的损失特征矩阵L。图2给出了第11处子模块位置接地且接地过渡电阻为1047 Ω时的损失特征矩阵，其中故障位置取1～16的离散值，接地过渡电阻在0～1900 Ω取20个离散值，另外，为了增强L1损失在低值区间的辨识度，取1L1进行绘制。

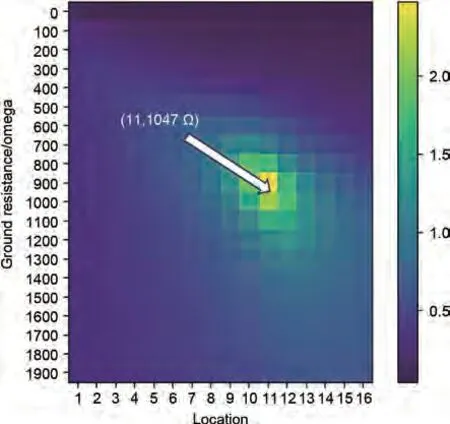
图2 n=11，r =1047 Ω的损失特征矩阵Fig.2 Loss Characteristic matrix with n=11 and r =1047 Ω

基于损失特征矩阵的定位方法，通过寻找损失特征矩阵中的最优值li*,j*，来确定故障位置为ni*。此时，故障定位问题可描述为最优化问题。

2.3 局部收敛性分析

为确保最优解(ni*,rj*)是拓扑矩阵中最接近实际故障位置和过渡电阻的参数组合，需要分析问题(9)的最优解存在性与唯一性。

为分析简便，式(2)的网侧等效阻抗统一表示为Zeq=r+jX，则式(3)所示零序电流计算相量为

子模块电压主要是基频和等效开关频率成分[25]，则故障位置为ni时的等效电压Ue(ni)，即式(1)为

式中，Sf1为基频系数；Sfs为开关频率系数；Uf1为子模块基频电压；Ufs为子模块的开关频率无相移电压。

零序电流估算结果的基频成分和等效开关频率成分均可表示为

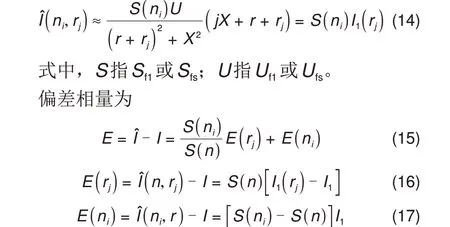
式中，I为零序电流相量；E(ni)为故障位置预测偏差；E(rj)为接地电阻预测偏差，E(rj)相对于|rj-r|单调变化。对于基频成分，E(ni)与零序电流同相或反相，幅值相对于|ni-n|单调变化；对于开关频率成分，在[n-N2,n+N2]内是单调的。并且，E(ni)与E(rj)不同相。因此，问题(9)的最优解存在且唯一，且最优解为M中最接近实际故障位置和过渡电阻的参数组合。对于开关频率，最优解唯一性限制在[n-N2,n+N2]；当|ni-n|较大时，基频偏差占主要部分，最优解唯一性问题不显著。

问题(9)的最优解存在且唯一，因此最优解中的ni*是故障位置的可信诊断结果。在故障接地过渡电阻不确定的情况下，该方法实现了对接地位置的有效诊断。

3 最优计算

对确定规模的CHB-BESS，拓扑矩阵的ni取值不超过模块数；但rj变化范围较大，易形成规模较大的拓扑矩阵。此外，损失特征矩阵的颗粒度越小，最优解越接近理论解，但是会扩大矩阵规模。如果遍历计算得到损失特征矩阵，计算开销较大，因此必须采用加速算法进行优化，本工作采用梯度下降优化算法进行加速计算。

鉴于问题(9)具有最优解唯一性，可采用梯度方向法进行优化方向选择，该方向通过计算故障预测偏差函数的梯度得到。当t时刻的条件为(ni,rj)时，取两个采样点，计算近似偏导。

式中，(kN,kr)用于描述采样方向，有(1,±1)两个组合交叉使用。经验证，该方法考虑到了双向增幅，比(0,±1)与(±1,0)的采样方式更加准确。

得到下一步的组合为：

式中，αni与αrj为两个方向的优化步长，以基频参数进行近似。步长考虑到了rj和e，能够实现快速优化。

梯度下降的寻优方法使得故障定位不需要计算出完整的损失特征矩阵，并且动态优化步长解决了损失特征矩阵的颗粒度问题。该方法解决了基于损失特征矩阵的定位方法由遍历计算带来的计算复杂度问题，使其在接地电阻不确定的情况下能够保证定位速度。

4 实验验证

4.1 实验平台

为进一步验证本工作提出的故障定位方法在不同接地故障电阻下的有效性，搭建了实验平台并进行检验。所搭建的实验平台如图3所示，主要包括实验室级别的CHB-BESS、变压器电源、网侧线路等效电路与模拟接地开关。其中，CHB-BESS的参数如表1 所示。等效电路用于模拟1 km 的电缆线路，其参数参考现有文献[26]中10 kV 电缆线路的典型参数，并按照等标幺值方式折算到380 V，如表2 所示。在实验过程中，通过人为控制接地开关的通断，来模拟不同子模块位置的接地故障。其中，接地故障的初始相位可以人为设置，其参考相位是网侧电压的锁相结果。通过接入不同阻值的电阻来模拟不同过渡电阻情况下的接地故障。并通过Ubuntu 与FPGA 的UDP 通信实现录波。其中，故障子模块位置被设置为第1、4、8、12、16 处，故障接地电阻被设置为33 Ω、66 Ω、130 Ω、330 Ω，以验证所提定位方法在不同阻值的接地电阻下对过渡电阻的鲁棒能力。

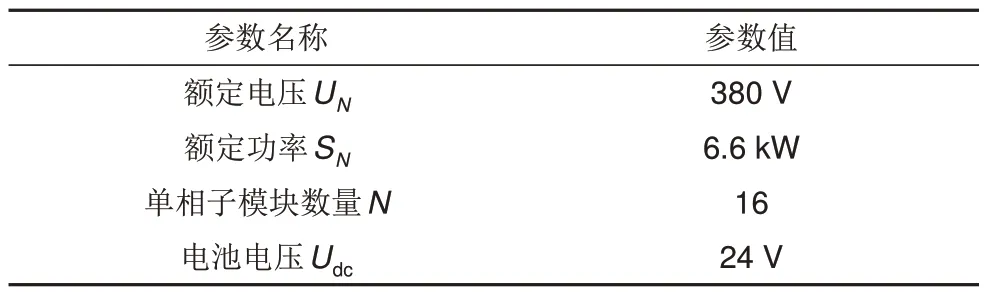
表1 CHB-BESS 参数Table 1 CHB-BESS parameters

表2 π等效电路参数Table 2 Equivalent circuit parameters

图3 实验平台：(a) CHB-BESS；(b) 模拟接地的开关；(c) 网侧线路的等效电路Fig.3 Experimental platform: (a) CHB-BESS; (b) switch for ground fault; (c) equivalent circuit of grid side line

4.2 实验结果与分析

图4给出了在第12处接地故障时，在不同过渡电阻下的零序电流。如图可知，当接地过渡电阻在较大范围变化时，即使在相同的故障位置，零序电流也会呈现显著的变动。因此，当接地过渡电阻不确定时，无法通过解析数学模型计算得到可信的零序电流。

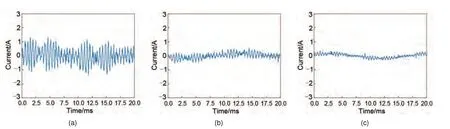
图4 零序电流：(a) 12处33 Ω；(b) 12处130 Ω；(c) 12处330 ΩFig.4 Zero sequence current: (a) No.12, 33 Ω; (b) No.12, 130 Ω; (c) No.12, 330 Ω

表3给出了不同接地电阻情况下，采用本工作所述诊断方法对5处接地位置的故障诊断结果。结果表明，在不同的接地电阻情况下，均能实现较准确的故障定位。

表3 实验结果Table 3 Experimental result

表4给出了不同故障定位方法的对比分析。其中，鉴于零序电流的基频和等效开关频率等频率成分是关键特征，并且各频率成分相对独立地提供故障位置信息， 支持向量机(support vector machines, SVM)取零序电流频谱作为输入特征向量，以实现对16 处子模块位置的分类目标；其数据集包含16 个接地位置，并且在每个位置都设置了不同的接地电阻，以模拟多样的接地情况。相比于SVM 以及较粗粒度的遍历检查方法，本工作提出的方法具有更小的定位误差，是更精确的故障定位方法，对接地过渡电阻具有更好的鲁棒性。粗粒度的遍历检查方法不仅在接地过渡电阻的鲁棒性方面表现较差，而且诊断速度较慢。细粒度的遍历检查方法会提升诊断的准确程度，但是会造成更慢的诊断速度。此外，虽然SVM 方法诊断速度更快，但是其对故障接地电阻的鲁棒性较差，需要大量的训练数据，不具备良好的可解释性，并且在不同的CHB-BESS之间迁移需要额外的工作。

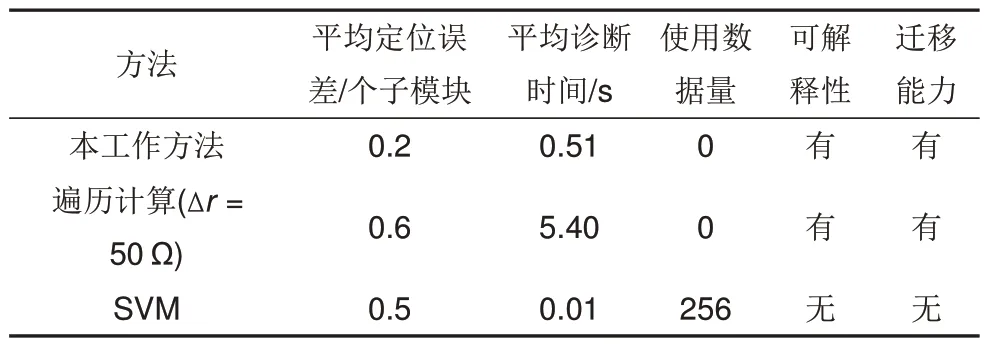
表4 不同方法的对比Table 4 Comparison of different methods

5 结 论

本工作提出一种基于损失特征矩阵的故障定位方法，在接地过渡电阻较大范围不确定的情况下可实现准确的故障定位，并将其应用于CHB-BESS模块间接地故障，通过实验验证了该方法的有效性，得到如下结论：

（1）在接地过渡电阻不确定的情况下，基于损失特征矩阵的故障定位方法仍可获得准确的故障发生位置，其平均定位误差仅为0.2个子模块；

（2）梯度下降优化算法是有效的加速方案，能够将本工作所提诊断方法的定位速度提高至少10倍。

本工作提出的方法为CHB-BESS 模块间接地故障的故障定位提供了一种解决接地过渡电阻不确定性问题的思路，并给出了相应的加速方案。下一步将重点研究小电流等情况下的故障定位问题，并对方法进行改善。