基于ADBF 的多通道SAR 抗干扰样本选择方法

王远征，庄 龙，王跃锟

（南京电子技术研究所，江苏南京 210039）

0 引 言

合成孔径雷达（Synthetic Aperture Radar, SAR）是一种高分辨率成像雷达，可以实现全天时全天候成像，在战场侦察、资源勘探以及地形测绘等方面具备其他对地观测传感器所不具备的优势[1]。作为一种宽带雷达系统，SAR 在其工作频段内容易受到多种复杂电磁干扰的影响，这些干扰信号会影响后续成像、检测和识别的效果。因此，SAR 抗干扰技术对提高SAR 在复杂电磁环境中的生存能力和实用效能具有重要的现实意义[1]。

随着SAR 应用的不断深入，单通道SAR 图像信息量较少，抗干扰能力较差，其性能难以满足应用需求，故SAR 经历着从单通道向多通道的发展过程[2]。多通道SAR 通过扩展空间维度，结合阵列信号处理中的自适应波束形成（Adaptive Beam Forming, ADBF）技术，利用空域自由度实现干扰抑制。

自适应波束形成（ADBF）技术是通过对各阵元加权进行空域滤波，以达到增强期望信号、抑制干扰信号的目的，且可以根据信号环境的变化自适应地改变各阵元的加权因子[3]。在波束形成过程中，准确构造干扰加噪声协方差矩阵是抑制干扰信号的关键。在选择样本数据计算干扰加噪声协方差矩阵时，若选择包含期望信号的样本，则波束形成器在自适应抑制干扰时会将期望信号误判为干扰进行抑制，致使波束形成器的性能显著下降[4]。

本文介绍了多通道SAR 回波信号模型及自适应波束形成原理，并利用SAR 回波信号在方位向频域内的性质提出了一种自适应样本选择方法，通过仿真结果评估该方法的有效性。

1 多通道SAR 抗干扰

1.1 多通道SAR 回波信号模型

方位多通道SAR 是SAR 领域的重要发展方向之一。与单通道SAR 相比，方位多通道SAR 利用空域自由度可以通过自适应波束形成（ADBF）技术进一步提升抗干扰能力。

以机载平台为例，干扰环境下多通道SAR 工作模型如图1 所示，真实通道位置和等效相位中心示意图如图2 所示。

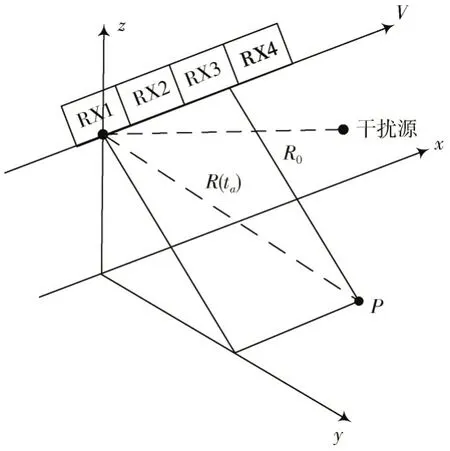
图1 干扰环境下多通道SAR 工作模型

图2 真实通道位置和等效相位中心示意图

假设方位多通道SAR 系统有4 个通道，相邻通道沿方位向的间距为D。第一个通道是发射通道，定义为参考通道，全部4 个通道均可以接收回波信号，且各通道之间天线参数、特性一致，不存在通道误差。经过等效相位中心处理后，多通道SAR 系统“一发多收”的工作模式就可以等效为各个通道在各自相应的等效相位中心的“自发自收”工作模式。相邻通道等效相位中心距离为d=D2，各通道等效相位中心与参考通道等效相位中心之间的距离为xm=(m- 1) ×d，m= 1,2,3,4。

定义载机以速度V匀速飞行，飞行方向为方位向，与其垂直的方向为距离向，载机距离地面的高度为H，P点为波束照射范围内的一个静止目标，方位向ta时刻载机距离目标P的距离为R(ta)，R0为载机与地面点目标之间的最短距离。在任意ta时刻，雷达平台参考通道距地面静止点目标的斜距R(ta)为：

参考通道发射的线性调频信号可以表示为：

式中：f0为载频；tr为距离向时间；Kr为线性调频信号的调频率；ϖr(tr)= rect(tr Tr)为信号的脉冲包络。参考通道接收的信号经过正交解调去载频后的回波表达式为：

式中：ta表示方位向的时间；Δta为波束中心的偏离时间；ϖa(ta)为方位向包络。经距离脉冲压缩处理后，设第m（1 ≤m≤4）通道接收的回波为sm(tr,ta)，则第m通道和参考通道之间的关系为：

将其变换到二维频域可得：

式中：fr和fa分别为距离频率和多普勒频率。

在实际情况中，SAR 回波信号会受到干扰信号的影响，干扰机将发射波束直接对准SAR 天线或者散射单元进行发射以达到最大的干扰功率[5]。各通道接收到的信号主要由真实目标回波信号、干扰信号和噪声组成[6]，可以表示为：

式中：x为雷达接收信号；s为真实目标回波信号；i为干扰信号；n为噪声信号。当SAR 在成像过程中受到压制干扰影响时，根据信号相对带宽大小及调制方式，干扰信号可以分为窄带干扰、调频调制宽带干扰和正弦调制宽带干扰[1]三类，其干扰抑制方法根据处理方式的不同可分为参数化[7]、非参数化[8]、半参数化[9]干扰抑制方法。由于多通道SAR 能够提供更多的自由度，因此在抑制压制干扰方面，可以应用阵列信号处理中的自适应波束形成技术，达到增强期望信号、抑制干扰的目的。

1.2 自适应波束形成基本原理

自适应波束形成的基本思想为：利用各阵元接收信号的先验信息，根据自适应准则不断调整权值系数ω，使得输出保留期望信号，滤除干扰信号，在天线上表现为形成具有一定指向性的波束方向图，将主瓣指向期望信号方向，将零陷指向干扰信号方向，并能够根据实际需要和环境变化动态地调整波束指向和零陷方向[10]。

以一维M元等距线阵为例，假定阵列接收到一个期望信号d(t)、J个干扰信号ij(t)以及加性白噪声n(t)：

式中：a(θk)=[a1(θk),a2(θk),…,aM(θk)]T为来自方向θk(k=d,i1,i2,…)的信号方向矢量。当快拍数N→∞时，波束形成器输出y(t)=ωHx(t),t= 1,2,…,N的平均功率为：

除式（8）外，阵列输出功率还可以表示为：

若保证从期望信号方向入射的信号能够无失真通过的同时，阵列输出功率最小[3]，则波束形成器最优权矢量的约束条件为：

利用拉格朗日乘子法求解可得最优权矢量为：

式中R=σ2s a(θd)aH(θd)+Ri+n。

则：

因此上述优化问题可以转化为：

其物理意义是基于期望信号被无失真接收的条件下最小化干扰加噪声的功率，相应的最优权矢量为：

在实际应用中，由于Ri+n无法获得，因此根据信号的时间平稳性，利用接收的采样数据对其进行估计，可表示为：

式中：x(k)为M× 1 维的第k个接收数据矢量；N为快拍数据个数。该方法即为协方差矩阵求逆（Stimulate Covariance Matrix Inversing, SMI）算法，利用该方法得到的最优权矢量为：

2 多通道SAR 自适应波束形成样本选取方法

SMI 算法的核心是干扰数据样本的选取和协方差矩阵R̂x的估算[11]。在选择样本数据估算协方差矩阵时，若选择的样本数据中包含期望信号，则波束形成器在自适应抑制干扰时会将期望信号误判为干扰进行抑制，致使波束形成器的性能显著下降[4]。因此估算协方差矩阵时，选择合适的样本对干扰抑制效果尤为重要。

目前文献中主要采用空间谱重建[12]、子空间重建[13]等方法重构干扰加噪声协方差矩阵，通过积分或特征分解等计算方法代替SMI 算法中样本选择过程，计算复杂度较高，要求已知期望信号的入射角度，且易受阵列扰动的影响[4]。本文主要研究在多通道SAR 背景下利用ADBF 方法抗干扰时如何选择合适的样本数据估计干扰加噪声协方差矩阵。

当雷达与目标之间存在相对径向运动时，多普勒频率可以表示为fd= 2V λ，V为雷达与目标之间的相对径向速度，λ为信号波长。随着平台的前进，雷达不断地发射和接收脉冲，发射脉冲间隔[14]为1 PRF s。目标被不同脉冲照射，每个脉冲的回波信号强度由方位向波束方向图决定，方位向波束宽度为θbw= 0.886λ La，La为方位向天线长度。

在方位频域维对SAR 回波信号进行处理，则波束中心穿越时刻等效转换成频域中的多普勒中心频率，其正比于雷达与目标之间距离R(ta)的变化率。

式中：ta_c为零多普勒时间；sinθr,c为ta=ta_c处的斜视角。

由多普勒中心频率可得目标的方位向带宽为：

上述方位向带宽即为目标在雷达3 dB 波束照射期间产生的频率漂移[15]。为使得方位向不发生频谱混叠，脉冲重复频率（Pulse Repeat Frequency, PRF）要大于多普勒带宽[16]Ba。因此在计算方位向频谱幅度时，中心频率区域为目标区域，两侧幅度较低的区域为干扰和噪声，可根据该特性确定干扰加噪声信号存在的区域。

该方法的重点在于如何确定目标频谱集中的区域宽度，将其定义为主杂波宽度W。由于Ba为3 dB 波束宽度内的频率漂移，但波束方向图主瓣外沿及副瓣仍会接收到目标信号，因此若令W=Ba，则主杂波宽度外仍然会存在目标分量，在两侧干扰区选取样本时依然可能选到目标信号。因此定义展宽系数A，则主杂波宽度可表示为：

式中展宽系数A一般取1.4～1.8，目的是使主杂波宽度完全囊括期望目标，在主杂波宽度外仅存在干扰信号和噪声信号，其幅度最大值处即为受干扰和噪声影响最大的区域。选取该最大值附近的样本进行计算，即可得到较为准确的干扰加噪声协方差矩阵，继而得到较好的干扰抑制效果。

3 实验结果分析

在自适应波束形成过程中，若协方差矩阵中包含期望信号，则波束形成器在自适应抑制干扰时会将期望信号误判为干扰进行抑制。以均匀线阵为例，设载波信号波长为λ= 0.06 m，阵元数M=10，阵元间距d=λ2，期望信号入射角度为10°，干扰信号入射角度为30°，信噪比为30 dB。对选择不同样本时的波束形成性能进行仿真。

图3a）为选择干扰加噪声区域的信号计算协方差矩阵时得到的波束方向图。图3b）为选择混有目标区域信号计算协方差矩阵时得到的波束方向图。

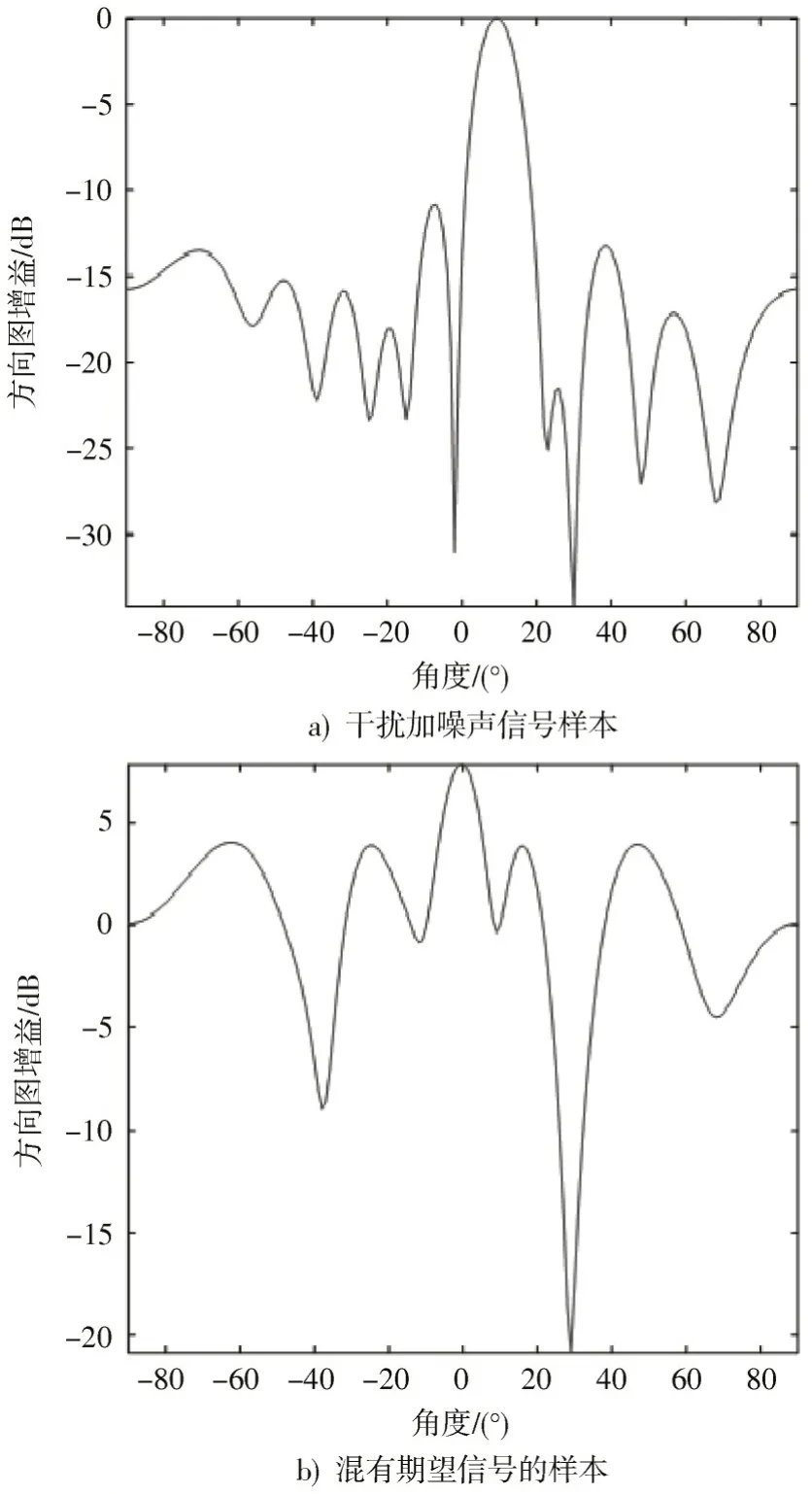
图3 选择不同样本计算协方差矩阵得到的方向图

由图3 可知：若选择干扰加噪声信号样本进行计算，则波束中心指向期望信号方向，并在干扰信号方向产生的零陷深度超过-30 dB；若选择的信号样本中混有目标，则波束中心发生偏移，且干扰信号方向零陷深度仅为-20 dB 左右。因此计算干扰加噪声协方差矩阵时，选择掺杂目标信号的样本对波束形成的结果产生了较大的影响。

本文提出了一种基于多通道SAR 自适应波束形成的样本选择方法，以多通道SAR 实测数据为例对该方法进行验证，实验参数如表1 所示。

表1 多通道SAR 干扰抑制实验参数

在干扰抑制前，该实测数据成像结果如图4 所示，在整个成像区域内存在条带式干扰，遮挡了有用目标。

图4 干扰抑制前的SAR 图像

将多通道SAR 回波数据转换至方位向频域，计算方位向频谱幅度均值，计算结果如图5 所示。

由图5 可知，目标幅度较大，集中在中心频率附近、主杂波宽度内，两侧旁瓣幅度较小的区域为干扰加噪声存在的区域。因此可以从中心频率出发，向两侧延伸，选择适当的展宽系数，待主杂波宽度边缘频率点即-W2 和W2 到达幅度主瓣波谷处，则可认为目标分量全部位于主杂波宽度内，此时-W2 ＜fs＜W2，fs为目标信号方位向频率分量。剔除主杂波宽度内目标幅度分量，剩余旁瓣部分幅度最大值为max{Amp}|fJ，其中-PRF 2 ＜fJ＜-W2&W2 ＜fJ＜PRF 2，fJ为旁瓣干扰加噪声信号频率分量。该最大值处附近即为无目标且干扰强度最大的信号区域。选择该区域内的回波信号计算协方差矩阵，进行波束形成，得到的干扰抑制结果如图6 所示。

图6 采用自适应样本选择方法得到的SAR 图像

在计算协方差矩阵时，采用直接样本选择方法得到的数据中易混有目标信号，其干扰抑制效果如图7所示。

图7 数据样本中混有目标信号得到的SAR 图像

图6 与图7 相比，目标区域的信号保留得较完整，干扰信号得到了较好地抑制。

对不同情况下输出信号的干噪比和信噪比的均值进行比较，如表2 所示。

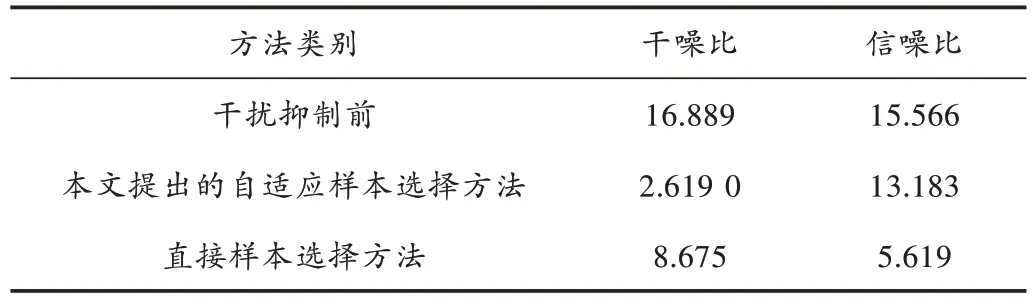
表2 不同情况下输出信号干噪比和信噪比均值dB

在干扰抑制前，输出信号的干噪比均值为16.889 dB，信噪比均值为15.566 dB。若利用本文提出的自适应方法选择样本并进行干扰抑制，输出信号的干噪比均值为2.619 0 dB，信噪比均值为13.183 dB，与干扰抑制前相比，其信噪比相差不大，干噪比明显下降，说明干扰信号抑制效果较好，目标信号没有受到较大影响。若直接选择的样本中混有目标信号，则输出信号的干噪比均值为8.675 dB，信噪比均值为5.619 dB，与干扰抑制前相比，信噪比下降较大，说明目标信号受到了较大影响，被误判为干扰进行抑制，与自适应样本选择方法相比，干噪比较高，干扰抑制效果不佳。

上述实验结果进一步说明了样本选择在自适应波束形成中的重要作用，以及本文提出的自适应样本选择方法的有效性。

4 结 论

自适应波束形成技术是阵列信号处理中增强期望信号、抑制干扰信号的有效方法，可将其应用于多通道SAR 抗干扰中，改善成像效果。在计算各阵元的最优权矢量时，需要确定回波中的干扰加噪声信号样本，以避免协方差矩阵中包含期望信号，影响抗干扰性能。本文提出了一种多通道SAR 抗干扰中自适应样本选择方法，通过计算回波信号方位向频谱幅度均值，确定主杂波宽度，选取该区域外最大值附近的信号，即可得到干扰加噪声的信号样本。通过实测数据验证了该方法的有效性，得到了较好的干扰抑制效果。

注：本文通讯作者为王远征。