Lamb波模态体声波压电谐振器仿真研究

崔向东,赵 颖

(中国人民解放军军事科学院 系统工程研究院,北京 100142)

0 引言

现代通信技术的快速发展使得传统的大体积石英晶振等逐渐被淘汰,取而代之的是性能更好、体积更小的微机电系统(MEMS)器件。同时射频器件对高性能时钟电路提出了更高的要求,信号处理器件需要具有低插入损耗、高带宽、低温漂等特性,而声学MEMS谐振器恰好满足此需求。目前主流的声学谐振器包括声表面波(SAW)谐振器和体声波(BAW)谐振器。其中SAW谐振器由于激励的频率较低,只能应用于低频段器件,而BAW谐振器工作频率在兆赫兹～吉赫兹频段,且其具有体积小,品质因数(Q)高,功率承载能力强,以及与集成电路工艺易兼容等优点[1]。但是传统的BAW谐振器的谐振频率主要由压电层厚度决定,而厚度方向激励的体声波难以同时满足高频和大带宽的需求[2];结合了各种压电材料的特性并在谐振体激励兰姆(Lamb)波模态,则能使谐振器兼容SAW器件的多频段和薄膜体声波谐振器(FBAR)器件的高频特性,从而实现具有较高频率和Q值、多频段可集成的压电BAW谐振器[3-5]。近年来科研人员对提高Lamb波模态谐振器的性能参数展开了诸多研究,主要围绕提升谐振器的Q值、谐振频率、机电耦合系数等参数进行探讨。其中Q值反映了谐振器的能量耗散水平,体现在滤波器的插入损耗和振荡器的相位噪声等方面;机电耦合系数反映了机械能与电能之间的转换效率,谐振频率和机电耦合系数体现在滤波器工作带宽等方面。对于Q值的提升,主要从能量损耗机制方面进行研究,如锚固损耗、空气阻尼、热弹性阻尼等[6]。锚固损耗为谐振器振动时,声波通过谐振腔与衬底之间的连接部位损耗能量,该损耗可通过优化锚的结构或选择刚度较大的材料制作锚,以减小锚损阻尼。

本文围绕锚系绳的设计和压电材料的选择进行研究,建立了基于叉指换能器的压电BAW谐振器模型,并利用有限元分析软件对4种锚结构产生的锚损以及3种压电材料给器件带来的性能进行讨论,器件激励在Lamb波S0模态工作。此外,本文对由BAW谐振器构成的BAW滤波器进行仿真实验,分析其所能实现的频带范围。

1 Lamb波谐振器工作原理

Lamb波是一种体声波,由纵(L)波和垂直剪切(SV)波结合形成,故而在振动方向上具有两个分量,一个是与声波传播方向平行的L分量,另一个是与声波传播方向垂直且与厚度方向一致的SV分量。常见的兰姆波谐振器通过对顶部叉指电极和底部板电极施加电信号,激励中间压电层产生压电效应发生形变,在谐振腔内反射形成驻波引起谐振,从而激励声波[7-8],其基波共振频率为

(1)

式中:v为压电层体声波相速度;λ为体声波波长;P为叉指电极周期。兰姆波的振动频率主要受压电层厚度的影响,所以具有频散特性,可分为对称(S)兰姆波和非对称(A)兰姆波,其中S型兰姆波的特征方程[9-10]定义为

(2)

A型兰姆波的特征方程定义为

(3)

其中:

(4)

(5)

式中:ci和ct分别为纵波和横波波速;ω,k分别为固有角频率和波数;H为压电层厚度。

通过对谐振器的等效电路模型进行理论分析可以提取出器件的关键性能参数。基于压电效应的谐振器等效MBVD模型如图1所示。

图1 压电谐振器等效MBVD模型

图1中,Rs为因金属互连引起的损耗,Rm为谐振器在谐振时的损耗。由Cm、Rm、Lm组成的分支称为运动臂,由C0、R0组成的分支称为静态臂。根据该等效电路模型,谐振器的谐振频率fr和反谐振频率fa分别为

(6)

(7)

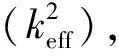
(8)

(9)

2 谐振器结构设计和模型建立

本文所设计的兰姆波压电谐振器采用电极-压电层-电极的三明治结构,如图2(a)所示,其中顶电极设计为叉指(IDT)电极,底电极为板电极,电极材料选用钼(Mo),该材料是MEMS中常见的具有高声阻抗和低电阻率的金属材料,作为电极能够有效提高器件Q值[12]。为了激励S型Lamb波模态(见图2(b)),在叉指电极上交替施加极性相反的电压,底部板电极作为接地端,使顶电极与底电极之间的压电层内部形成极性相反的电场,从而产生方向相反的形变。器件压电层厚度H=1 μm,叉指电极间距P=62.5 mm,电极厚度Hm=200 nm,电极宽度W=25 μm,谐振器全长L=1 425 μm,有效孔径Le=1 260 μm,电极个数n=6。为了有效计算产生锚固损耗后谐振器的Q值,本文建立了基于完美匹配层(PML)的有限元模型,将边缘衬底设定为PML,以吸收通过支撑梁耗散出去的能量。此外,由于电极层和压电层厚度相对于器件的长度和宽度,尺寸差异非常大,相当于一个薄板结构。在网格划分过程中,压电层选用自由四面体网格,并控制自由四面体网格在x、y、z方向上以3∶2∶20的比例进行缩放,在边缘衬底部分采用映射网格并进行扫掠,建立的网格剖分如图3所示。

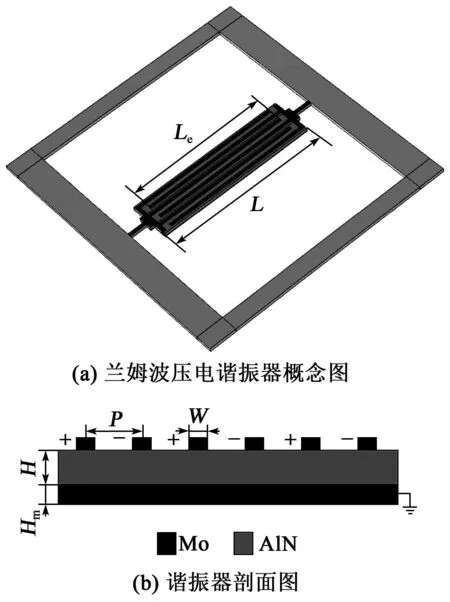
图2 谐振器几何图

图3 谐振器模型网格剖分

3 器件不同锚结构设计与仿真

本文利用有限元分析软件建立了4种不同锚系绳结构的BAW谐振器模型,并分析锚结构对器件Q值的影响。谐振腔通过支撑锚与边缘二氧化硅(SiO2)衬底部分连接,谐振腔底部为镂空部分,实现了腔体底部与空气的阻抗不匹配,有效形成声波反射。边缘衬底边界条件设置为PML域,使其有效吸收声波并计算Q值。在有限元分析软件的特征频率研究中引入Q值的计算方式,有:

(10)

式中ω为求解的器件固有角频率。在器件存在阻尼的情况下,角频率具有虚部Im(ω)和实部Re(ω),虚部与实部之比反映了阻尼的大小。

所构建的4种锚结构分别为直梁型、梯形梁、框架-梁型及末端带槽型支撑锚。对于支撑锚的设计,当支撑锚的共振频率与谐振体的共振频率相匹配时,造成的锚损失最严重,而对于给定的锚结构宽度W,若要达到频率匹配,则支撑锚的长度L需满足[13]:

(11)

(12)

式中:E为谐振腔杨氏模量;ρ为密度;f0为共振频率;λi为特征模态相关系数。为了避免支撑锚与谐振腔发生频率匹配,锚的长度设计需要远离L,通常将支撑锚设定为λ/4的奇数倍(其中λ为波长),以达到最大的阻抗失配。本文将锚长度设定为5λ/4,且为了控制锚与谐振腔的接触面面积对器件性能的影响,所构建的4种锚与谐振腔的接触面宽度相同。图4是4种锚结构下的谐振器有限元位移仿真图。

图4 4种支撑锚结构下谐振器位移图

由图4可以看出,各种锚结构的支撑轴区域均存在一定位移,这表明有部分能量通过支撑锚泄露到衬底中而引起能量损耗。直梁型支撑锚的锚点处产生的位移幅度最大;其次是梯形梁支撑锚,位移以波纹形状产生,代表能量泄露较严重;框架-梁型和末端带槽型锚点处的位移最小,能量耗散最少。对4种锚结构下的器件进行频域分析,得到导纳曲线如图5所示。由图可见,4种锚结构下的谐振器谐振频率在70.374 MHz附近,品质因数(Q)分别为1 221.9、1 244.9、1 338.1和1 292.4,其中框架-梁型的品质因数最大,其次为末端带槽型。

图5 4种支撑锚结构下谐振器仿真导纳曲线

对上述结果进行分析可知,由于框架-梁混合结构具有较小的刚度和振幅,而末端带槽型结构能够在末端槽边界处将泄露到衬底的声波反射回去,从而降低了锚损。

为了进一步探究支撑梁与谐振体接触面积对器件性能的影响,研究了框架-梁型锚结构下锚的宽度D分别为20 μm、30 μm、40 μm时器件的导纳曲线,如图6所示。这3种宽度下的谐振频率都为70.372 MHz,品质因数分别为1 344.5、1 332.7、1 286.7。经分析可知,随着支撑梁宽度的增加,谐振器品质因数降低,这是由于支撑梁与谐振体的接触面积增加,导致更多的声波能够通过支撑梁扩散到衬底中而造成了更多损耗。由图可见,3种宽度下的支撑梁导纳曲线几乎重合,表明支撑梁的宽度大小对谐振器杂散模态和主模态影响较小。

图6 支撑梁宽度D为20～40 μm时器件导纳图

4 压电材料的选择

压电材料的特性会影响到BAW器件的机电耦合系数和品质因数。从器件性能出发,选用压电材料通常需要考虑压电耦合系数、介电常数和声速3个参数。其中压电耦合系数直接决定了机电耦合系数大小,介电常数决定了器件阻抗水平,而声速则与谐振频率相关,通常在压电层厚度一定时,声速越大,谐振频率越高。在谐振器设计过程中常用的压电材料有压电陶瓷(PZT-4)、氧化锌(ZnO)、氮化铝(AlN)等,其材料特性如表1所示。

表1 几种压电材料的特性参数

图7 不同压电材料下器件导纳曲线

根据仿真结果可知, PZT-4具有最大的机电耦合系数,能够实现更大带宽的BAW滤波器,但应用该压电材料时谐振器主模态附近的横向杂散模态严重;ZnO具有相对较高的品质因数,且横向杂散模态少于PZT;AlN因高声速而具有最高的谐振频率,主模态附近横向杂散模态最少,能够实现高频滤波器。虽然PZT压电性能好,但其性能易受到组分变化的影响,薄膜制备过程中难以保证其组分均匀;而ZnO不具备CMOS兼容性,相比之下,AlN具有与CMOS工艺相兼容的优点,且固有损耗较低,是制作BAW谐振器常用的压电材料[14]。

5 等效MBVD模型仿真

根据上述仿真分析结果,本文选取带有框架-梁支撑锚的氮化铝BAW谐振器,建立的等效MBVD模型见图1,参数如下:

(13)

C0=[2πf1(1+γ-1)Im(Z1)]-1

(14)

Cm=C0/γ

(15)

(16)

(17)

根据仿真所得导纳曲线,由式(13)-(17)提取出MBVD模型中的各项参数,得到模型的等效电学参数如表2所示。利用ADS软件建立等效电路模型并进行性能测试仿真,仿真的频率范围设定为68～74 MHz,步长设置为0.005 MHz,得到的S11参数曲线和导纳Y11曲线如图8所示。

表2 等效MBVD模型电学参数

图8 等效MBVD模型S11参数及导纳曲线

S11参数反映了输入回波损耗,该参数越小,表明回波损耗越低,能量传输效率越高[15]。由图8可知,在BAW谐振器工作频率处回波损耗非常小,在谐振区间外S参数接近0,表明器件插入损耗非常小。仿真导纳图所得参数与前述仿真结果贴合。

基于所设计的BAW谐振器单元,本文通过梯形级联方式搭建了由其构成的BAW带通滤波器并进行电学仿真,其中并联BAW谐振器参数与上述所提取的谐振器电学参数相同。根据带通滤波器工作原理及式(6),设置串联BAW谐振器的Lm=24 099.356 9 nH,其余参数与表2相同,得到的一阶带通滤波器频率响应曲线如图9所示。由图可知,滤波器为高频窄带滤波器,其通带内插入损耗仅为-0.9 dB,3 dB带宽为0.62 MHz,但其带外衰减较小,通带左侧阻带达到-5.872 dB,右侧阻带达到-7.457 dB,难以满足带通滤波器应用时的带外衰减需求,因此需要增加谐振器的级联数对带外衰减进行优化。

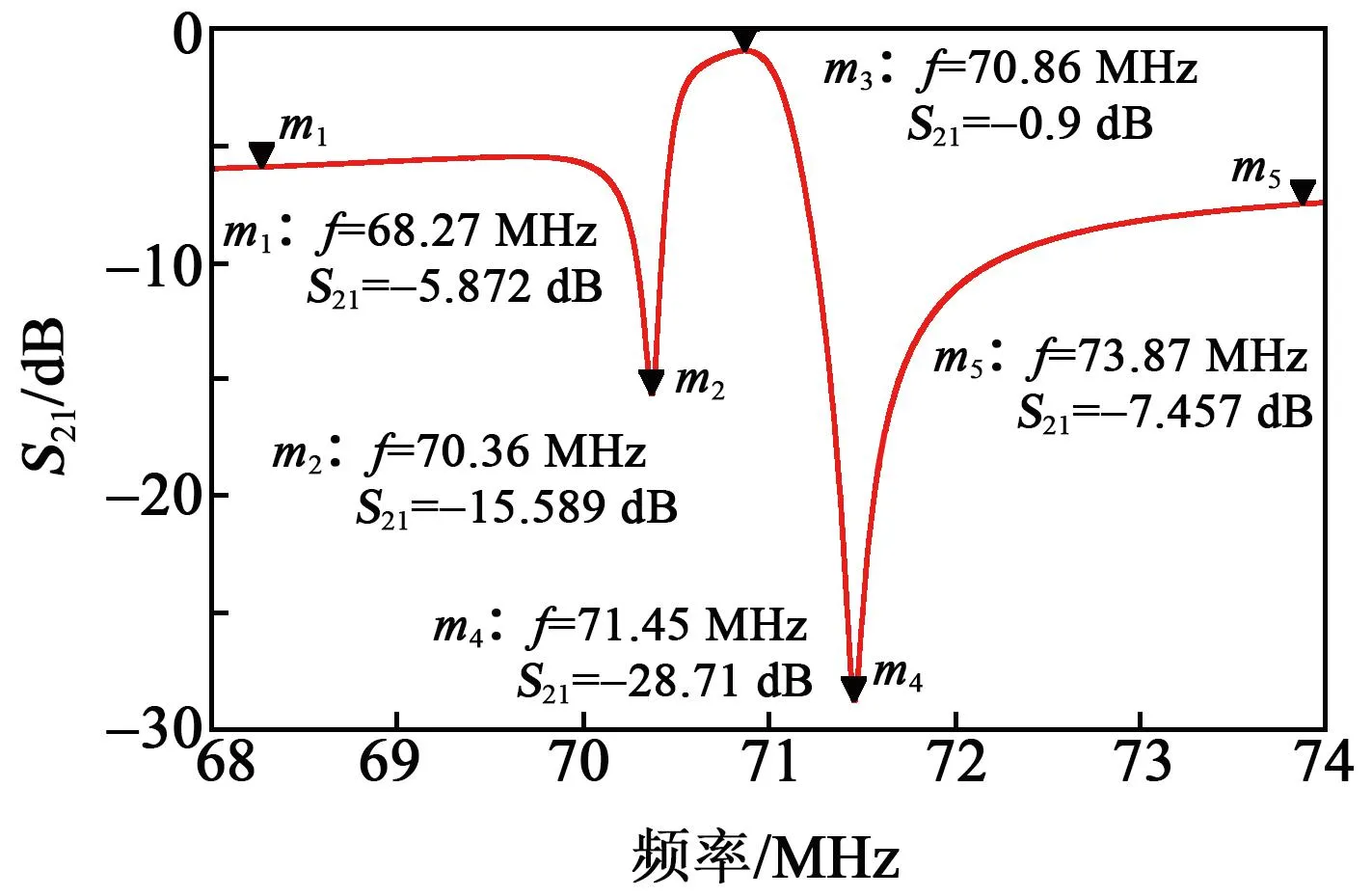
图9 梯形BAW带通滤波器频率响应特性曲线

通过增加上述BAW梯形滤波器的级联阶数,得到二阶、三阶BAW滤波器频率响应曲线如图10所示。由图可知,随着级联阶数的增加,滤波器的带外衰减明显增大,左侧阻带由-5.852dB增加到-22.907 dB,右侧阻带由-7.446 dB增加到-24.877 dB,表明带外抑制得到改善,而通带内插入损耗和带宽随级联阶数的增加,受到的影响较小,插入损耗>-1 dB,因此,所设计的BAW带通滤波器适用于高频窄带应用范围。

图10 不同阶数BAW带通滤波器频率响应曲线

6 结束语

BAW谐振器在应用过程中因存在诸多损耗机制而影响其品质因数,其中锚损是最主要的损耗机制之一。为了研究支撑锚结构对谐振器Q值的影响,本文对直梁型、梯形梁、框架-梁型及末端带槽型4种支撑锚结构下的BAW谐振器进行建模仿真,并将器件激励在兰姆波S0模态下工作,得到谐振器谐振频率在70.374 MHz附近,框架-梁型谐振器品质因数最高,达到1 338.1。同时还分析了不同支撑锚宽度下谐振器的谐振响应情况。经分析可知,随着支撑梁宽度的增加,谐振器品质因数降低,但对谐振器杂散模态和主模态影响较小。此外,为了研究不同压电材料对器件特性的影响,本文仿真分析了压电材料为PZT-4、ZnO、AlN时器件的导纳曲线,研究表明,PZT-4具有最大的机电耦合系数,ZnO具有相对较高的品质因数,AlN具有最高的谐振频率。但考虑到AlN的固有损耗较低,且具有与CMOS工艺相兼容的优点,因此,本文建立了带有框架-梁型支撑锚的AlN BAW谐振器的MBVD模型,并采用梯形级联方式构建了BAW带通滤波器进行仿真分析,最终得到插入损耗>-1 dB,频带在70.36～71.45 MHz的BAW滤波器模型。