Pasternak 地基中H(t)-V 受荷桩水平响应有限杆单元法分析

江杰 ，艾永林 ，柴文成 ，龚健 ，欧孝夺 †，邵云怡

（1.广西大学 土木建筑工程学院，广西 南宁，530004；2.广西大学 特色金属材料与组合结构全寿命安全国家重点实验室，广西 南宁，530004；3.广西瑞宇建筑科技有限公司，广西 南宁 530299；4.中船第九设计研究院工程有限公司，上海 200063）

桩基础作为海上风机、港口码头、桥梁和高速铁路等建设工程中所采用的重要基础型式，其在承受竖向力V的同时，还会承受来自波浪、风、地震等水平动荷载H（t）的作用［1-3］.在轴、横向静-动荷载作用下，桩基结构的受力变形分析往往较为复杂［4］，为此探讨复杂动力环境下桩基的水平振动响应，对揭示桩基的受力特性分析具有重要意义.

关于桩基水平振动响应的计算方法，目前常见的有分离变量法［5］、传递矩阵法［6］和有限单元法［7］.其中胡安峰等［5］和Mylonakis 等［6］基于动力Winkler地基模型，分别利用分离变量法和传递矩阵法计算得到水平简谐荷载作用下均质、层状地基中单桩的水平振动解析解，然而上述计算方法在复杂荷载和复杂边界条件下，数学推导涉及多项积分运算，求解过程较为繁琐，在工程中难以有效推广.有限杆单元法通过构造桩基的整体刚度方程，对复杂荷载和边界条件处理较为简便，计算结果可靠，在桩基础等杆系结构的受力分析中得到了广泛应用［8-13］.利用有限杆单元法，赵明华等［8-10］和黎学优等［11-12］进行了桩顶静力荷载作用下桩基的受力分析；进一步地，蒯行成等［13］基于动力Winkler地基模型，推导了单桩水平动力阻抗的计算方法；覃玉兰等［7］基于动力Winkler 地基模型求解了桩顶水平简谐荷载H（t）与扭矩T组合荷载作用下单桩的内力与位移.

上述研究普遍将桩周土体简化为Winkler 地基模型，用单一参数表示土体的连续性，虽计算简便，但相较双参数Pasternak地基模型忽略了地基土体的剪切效应，计算结果存在一定的误差［14］.因此，众多学者围绕Pasternak地基在桩基的动力响应中的应用进行了研究.例如，Bhaduri 等［15］和王珏等［16-17］将地基等效为Pasternak 地基，分别采用傅里叶变换和荷载传递矩阵法推导得到单桩的水平振动解析解.Qetin 等［18］探究了均质Pasternak 地基弹性参数对桩基自由振动响应的影响.值得注意的是，上述研究大多仅考虑水平动荷载作用对桩基的动力响应.

而在实际工程中，桩基往往承受水平和竖向荷载的共同作用［2］.对此，Halabe 等［19］求解了竖向静荷载作用下单桩的水平振动微分方程，认为竖向荷载对桩基的水平振动特性有显著的影响.吴鸣等［4］和熊辉等［20］分别建立桩-土动力相互作用模型，利用传递矩阵法得到了考虑竖向力影响的水平动力阻抗解析解.栾鲁宝等［2］通过引入势函数分析了竖向荷载作用下大直径管桩的水平振动响应，得出了管桩水平振动响应频域解析解.可以看出，上述已有桩基水平振动响应研究中，较少有利用有限杆单元方法综合考虑地基剪切变形和桩顶竖向荷载影响的相关研究.

鉴于此，本文结合有限杆单元方法，同时考虑桩周地基土体的剪切效应和桩身P-Δ 效应，构建基于Pasternak 地基模型的H（t）-V受荷桩水平响应有限单元数值解.通过与已有解析解、有限元解和模型试验进行对比验证方法的正确性.最后，探讨土体剪切效应、桩顶竖向荷载、水平简谐荷载幅值、无量纲频率和桩身长径比等参数对桩身位移和弯矩的影响规律，可为工程实践提供参考.

1 计算模型与基本假设

1.1 基桩受力简化分析模型

单桩受力简化分析模型如图1 所示，桩顶承受水平简谐荷载H（t）=H0eiωt，P0为竖向静荷载.其中，H0为激振力幅值，虚数i=，ω为动荷载圆频率，t为时间，桩的长度和直径分别为L和dp，z为地面以下计算结点深度，ks、cs分别为地基土体弹性系数与阻尼系数.

图1 桩基础简化分析模型示意图Fig.1 Simplified analysis model of pile

1.2 基本假设

为便于分析，基于上述计算模型的受力特征，引入如下基本假设：

1）桩体为圆形等截面桩，视为均匀、各向同性的Euler-Bernoulli梁；

2）桩周土体视为均质土体，简化为Pasternak 地基模型以描述桩土相互作用，其对桩的作用等效为一系列沿桩身分布的阻尼器、弹簧和剪切单元.其中阻尼系数cs和弹性系数ks与土体性质有关；

3）桩土体系振动满足小变形条件，处于线弹性范围内，桩-土完全接触，接触面保持位移协调，不发生相对滑移与脱离；

4）忽略水平简谐荷载作用引起的桩身竖向位移.

2 改进的有限杆单元法

本节将在传统有限杆单元法的基础上，对单元刚度矩阵和结点荷载向量做出修正，建立可综合考虑P-Δ 效应、土体剪切效应和桩侧摩阻力等因素的综合刚度矩阵方程，以期用于桩体水平振动响应的数值计算中.

2.1 基本平衡方程

将桩体离散为由有限个结点连接的杆单元，结点受力如图2所示.

图2 杆单元结点划分及受力分析示意图Fig.2 Schematic diagram of node division and mechanical analysis of beam element

式中：Fe为单元结点荷载向量；δe为杆端位移向量为单元刚度矩阵.

2.2 考虑P-Δ效应的单元附加刚度矩阵

在水平动荷载H（t）作用下，竖向荷载因桩身的水平偏移而产生附加弯矩，将进一步加剧桩身的挠曲变形，即桩身产生P-Δ效应.故本节将对上节传统杆单元刚度矩阵k0e进行修正，以考虑竖向荷载对桩身弯矩和水平位移的影响.根据杆单元虚位移原理，考虑P-Δ效应的单元刚度方程［9］可表示为：

式中：FNe为单元等效结点荷载向量；δe为杆端位移向量；PN()为距i单元上结点深度处的竖向荷载，可表示为PN()=P0+fs·(hi+)，hi为i结点距桩顶的距离，fs为桩侧摩阻力；Nv表示与杆单元水平位移对应的形函数矩阵，可表示为：

2.3 考虑双参数地基模型的单元附加刚度矩阵

Pasternak双参数弹性地基模型相较单参数Winkler 地基模型，考虑了地基土体剪切的效应，计算结果更精确［21］.基于Pasternak 双参数弹性地基模型的桩身挠曲微分方程为［22］：

式中：Ep、Ip、b0分别为桩身弹性模量、截面惯性矩和计算宽度；x为桩身挠度；Gs为土体剪切模量；K为地基反力模量.

首先基于动力Winkler 地基模型，桩周土产生沿桩身连续分布的水平抗力p（x），其与位移的关系式［7］可表示为：

式中：p（x）、mp、ω分别为桩周土对桩体的水平抗力、单位桩长的质量和谐振频率.其中，ks、cs取值由下式［23］确定：

式中：δ为与土体参数、荷载类型、桩土相对刚度和桩顶约束条件有关的函数，与深度z无关.当桩顶自由时，δ≈1.5～2.5；桩顶约束转角时，δ≈1.0～1.2.本文考虑桩顶自由时ks=2.1Es，桩顶约束转角时ks=1.2Es.为土层的剪切波速，Es、ρs、vs和βs分别为桩周土的弹性模量、密度、泊松比和阻尼比，a0=ωdp/Vs，为无量纲频率.

在此基础上，由式（6）知，当Gs=0时，Pasternak双参数地基模型即退化为Winkler 地基模型.当无Gs实测值时，可由Tanahashi［24］提出的经验公式确定：

式中：Es、vs同式（8）；ts为剪切层厚度.

梁发云等［25］基于Yao 等［26］的数值模拟结果，认为地基土剪切层厚度ts近似等于水平荷载作用对桩侧土的影响范围S（S=11dp，dp为桩径），故本文分析中取ts=11dp，实际上剪切层厚度ts与桩周土体的性质有关，本文对此不做深入研究.作用在杆单元上的荷载按照其作用位置不同，可分为结点荷载和非结点荷载两种.为建立各结点的平衡方程，需将分布作用在杆单元上的桩周土抗力（非结点荷载）按照虚位移原理等效为结点荷载Fe，可表示为：

2.4 考虑桩侧摩阻力的等效结点荷载向量

桩基础受外荷载作用后，将相对桩侧土体发生一定程度的偏转与沉降.如图3 所示，桩表面单元m处的竖向变形量为zm=dpsinα·θ()/2，单元面积为δAm=zmδα·dp/2，其中径向夹角为α，水平面偏转角为θ().基于虚位移原理，桩侧摩阻力所做的外力虚功δWτ的关系式［9］为：

图3 桩身单元变形图Fig.3 Unit deformation diagram of pile

综上所述，根据式（10）和式（11）可确定考虑土体剪切效应的单元刚度矩阵，再结合式（1）、式（5）、和式（15）可得到考虑桩身单元刚度、P-Δ 效应、土体剪切效应和桩侧摩阻力等因素的单元综合刚度方程为：

3 有限杆单元法求解内力、位移步骤

基于改进的有限杆单元方法，建立考虑上述因素的综合刚度矩阵，编制MATLAB 程序求解受荷桩基的内力与位移，主要包括如下计算步骤：

1）单元离散化：将桩基离散为若干具有较高计算精度的微单元和结点.其中结点位置可取集中力作用点、土层分界处、桩截面面积突变点、支承点等.

2）整体特性分析：结合式（1）、（5）、（10）和式（11），按照后处理法将单元刚度矩阵组装为整体刚度矩阵，并建立整体刚度方程.

3）结点位移求解：引入桩基的位移边界条件，求解整体刚度方程，得到桩身任意结点的位移向量δe.

4）杆端力求解：将结点的位移向量代入单元刚度方程式（1）中，求得杆单元的杆端力，进而确定桩身内力与水平变形量，绘制桩身水平位移与内力图.

4 算例验证

4.1 算例1

为验证本文解的合理性，将本文与文献［27］考虑竖向荷载影响的水平振动响应室内模型试验解、有限元解进行对比分析.计算参数如下：桩长L=0.9 m，桩径dp=0.06 m，泊松比vp=0.3；桩周土的密度ρs=1 900 kg/m3，弹性模量Es=8.5 MPa，泊松比vs=0.3，阻尼比βs=0.05；第一组桩顶组合荷载为f=3 Hz，水平动荷载幅值H0=500 N，竖向荷载P0=0 N；第二组桩顶组合荷载为f=2 Hz，水平动荷载幅值H0=150.2 N，竖向荷载P0=150 N；边界条件为桩顶、桩底自由.图4和图5 分别为两组桩在桩顶受不同组合荷载作用一个周期内桩身弯矩随深度z的变化曲线.

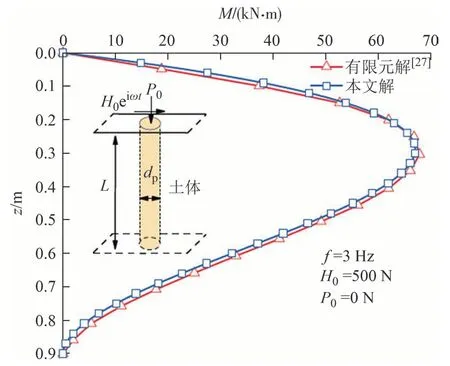
图4 第一组桩身弯矩对比图Fig.4 Comparison of the bending moment of the first group pile

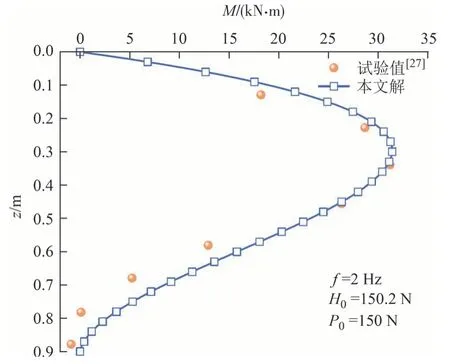
图5 第二组桩身弯矩对比图Fig.5 Comparison of the bending moment of the second group pile

由图4及图5可知，本文方法所得的桩身弯矩计算值与文献［27］的有限元值较为接近，两组桩身弯矩最大值均发生在距桩顶1/3深度处，桩身弯矩随深度的变化趋势一致.

4.2 算例2

为进一步验证本文方法的正确性，将本文解与文献［7］的水平振动响应解进行对比.令P0=0，即退化到水平简谐荷载H（t）作用下的水平振动响应解，并将本文退化解与已有案例解进行对比.相关计算参数为：桩长L=4.5 m，桩径dp=0.3 m，桩身弹性模量Ep=20 GPa，泊松比vp=0.2；桩周土的密度ρs=2 000 kg/m3，弹性模量Es=4 MPa，泊松比vs=0.4，阻尼比βs=0.05；边界条件为桩顶自由，桩底嵌固.图6 和图7 给出了水平动荷载幅值H0=100 kN，无量纲频率a0=0.5 作用一个周期内桩身位移、弯矩的最大值随深度z的变化曲线.

图6 桩身水平位移对比图Fig.6 Comparison of lateral displacement of the pile

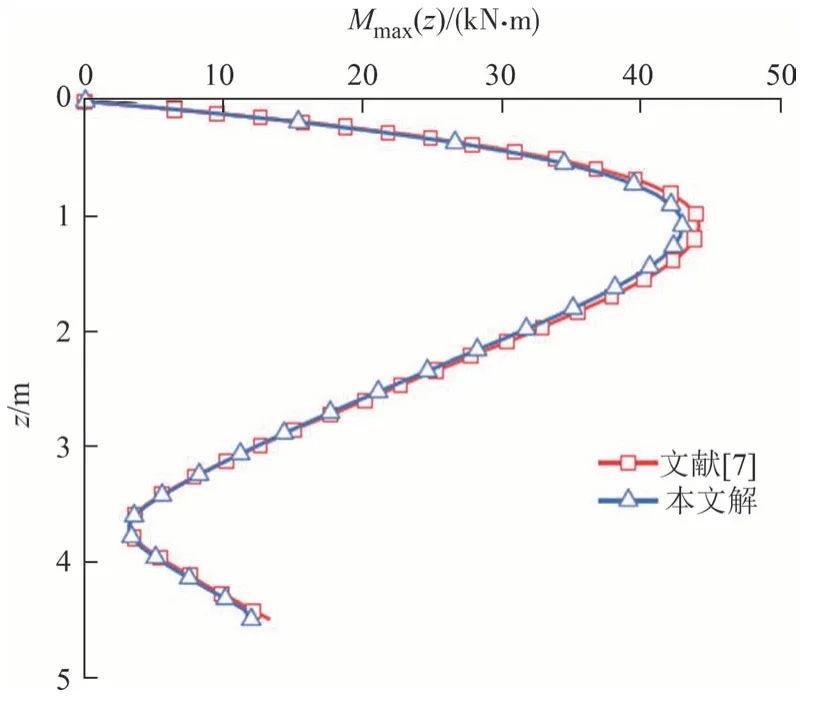
图7 桩身弯矩对比图Fig.7 Comparison of the bending moment of the pile

由图6、图7 可知，当水平动荷载幅值H0=100 kN时，桩顶最大位移出现在桩顶位置，最大值为14.12 mm；最大桩身弯矩发生在距桩顶1/3 深度处，最大值为42.96 kN·m，与文献［7］计算结果吻合较好.文献［7］基于Winkler 地基模型，忽略地基土体的剪切效应，使得桩体结构的受力计算结果较实际偏大.结合图6、图7 的对比验证结果，表明利用本文计算方法得到的桩身内力和位移与文献结果基本一致，验证了提出方法的准确性.

4.3 算例3

文献［28］基于Winkler 地基理论，得到了层状地基中单桩水平振动解析解，为进一步验证本文解的适用性，本文Pasternak 地基可退化为Winkler地基模型（Gs→0）.计算参数如下：桩径dp=0.3 m，桩长径比L/dp=10，15，泊松比vp=0.25，桩体密度ρp=2 500 kg/m3，弹性模量Ep=20 GPa；土层参数n=2，两层土的密度、阻尼比和泊松比取相同值，分别为ρs=2 000 kg/m3、βs=0.05和vs=0.4，桩土刚度比Ep/Es2=5 000，上下两层土的弹性模量比Es1/Es2=0.5；边界条件为桩顶约束转角，桩底固定.图8、图9 为水平动荷载幅值H0=100 kN，无量纲频率a0=0.5，竖向荷载P0=0，作用一个循环周期内桩身水平位移、弯矩的最大值随z/dp的变化曲线.为便于分析，对深度z处桩身水平位移和弯矩的最大值xmax（z）和Mmax（z）进行无量纲化处理，其中xˉ=Ep·dp·xmax(z)/(500H0)和=Mmax(z)/(2H0·dp).

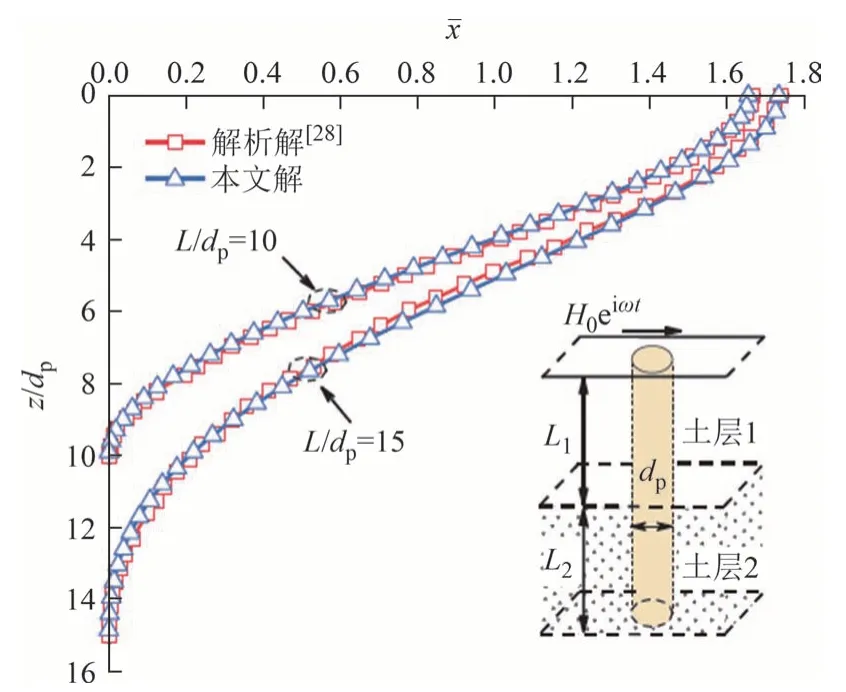
图8 桩身无量纲水平位移对比图Fig.8 Comparison of dimensionless lateral displacement of the pile

由图8、图9 可以看出，不同桩身长径比条件下，本文得到的桩身无量纲水平位移和弯矩与文献［28］已有解析解结果吻合较好，进一步验证本文方法的适用性.

结合上述算例的对比验证结果，可见当单元数划分合适，本文基于综合刚度矩阵的改进有限杆单元法对于复杂边界、荷载和层状地基等工况下得到的桩身内力和位移解与已有文献的解析解、有限元解和试验结果基本一致，计算精度较高，验证了提出方法的准确性和适应性.

5 参数分析

本节将侧重分析土体剪切效应、桩顶竖向荷载P0、水平简谐荷载幅值H0、无量纲频率a0和桩身长径比L/dp等参数对桩身水平位移、弯矩的影响.相关计算参数选取为：L/dp=20，桩径dp=0.3 m，桩身弹性模量Ep=31.5 GPa，泊松比vp=0.2；桩周土的密度ρs=2 000 kg/m3，弹性模量Es=15 MPa，泊松比vs=0.3，阻尼比βs=0.05，边界条件为桩顶自由、桩底固定.水平动荷载幅值H0=60 kN，无量纲频率a0=0.5，竖向荷载P0=200 kN.为便于对比分析，对深度z处桩身水平位移和弯矩的最大值xmax（z）和Mmax（z）进行无量纲化处理，其中x(z)=xmax(z)/xmax和M(z)=Mmax(z)/Mmax.

5.1 土体剪切效应的影响

为探讨土体剪切效应对桩身内力和变形的影响规律，图10 和图11 采用Pasternak 地基模型与传统Winkler 地基模型（Gs→0）计算了不同桩土弹模比Ep/Es和土体剪切模量Gs下单桩的无量纲水平位移与弯矩的变化情况，其中固定Es=15 MPa，Ep/Es分别取1 500、2 500 和3 500［7］；Gs=0、1.0Gs和5.0Gs.由图10、图11 可以看出：1）地基土体的剪切效应对约束桩身的内力和变形具有一定的贡献.当Gs=0 和1.0Gs时，采用Winkler 地基计算得到的桩身水平位移和弯矩大于Pasternak 地基所得结果，说明未引入土体剪切模量Gs将忽略地基土体的剪切效应，使得桩体结构的受力计算结果较实际偏大，因此，土体剪切效应对桩身水平振动响应的影响不容忽视.2）土体剪切模量Gs对桩身水平位移与弯矩具有削弱作用.当Ep/Es=2 500，Gs由0 增至5Gs时，桩身最大水平位移由0.856减至0.510，减小40.42%，最大弯矩由0.960 减至0.343，减小64.27%.3）Pasternak 地基和Winkler 地基计算所得的桩身最大水平位移和弯矩的差异性随着桩土弹模比Ep/Es的降低呈现出增强趋势.当土体剪切模量Gs=0 和1.0Gs，Ep/Es由3 500 降至1 500 时，桩顶水平位移逐渐增加，变化幅度由9.79% 增至13.33%；桩身最大弯矩逐渐降低，变化幅度由20.42%增至34.92%.故当桩土弹模比较小时，土体剪切效应对桩身水平振动响应的影响不容忽视.

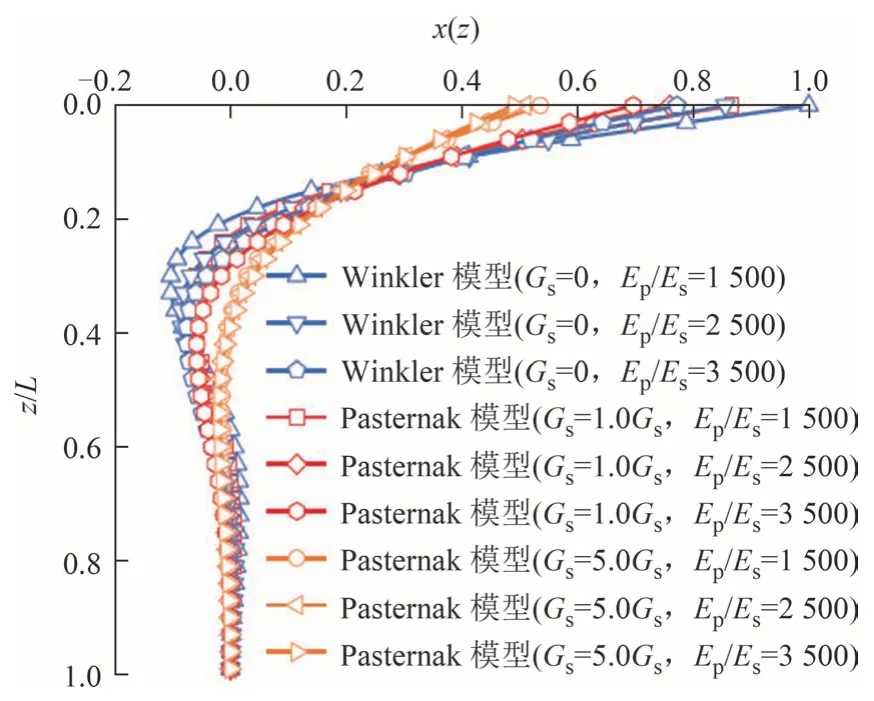
图10 基于两种地基模型的桩身无量纲水平位移对比图Fig.10 Comparison of dimensionless lateral displacement of the pile based on two foundation models

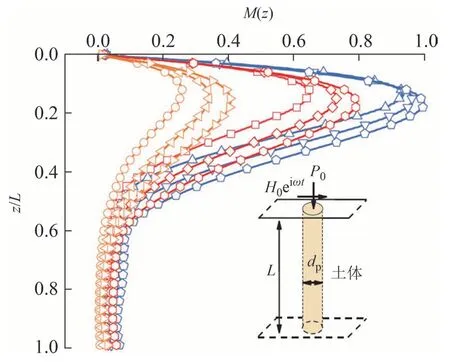
图11 基于两种地基模型的桩身无量纲弯矩对比图Fig.11 Comparison of dimensionless bending moment of the pile based on two foundation models

5.2 桩顶竖向荷载P0的影响

梁发云等［29］定义桩顶荷载H0=和P0=λH0，探究不同竖向荷载对桩身内力和变形的影响.图12 和图13 给出了竖向荷载特征参数λ取0、0.5、1和2 时桩身无量纲水平位移、弯矩随深度的变化.由图12、图13 可知：1）随着桩顶竖向荷载特征参数λ的逐渐增加，桩身无量纲水平位移和弯矩均显著增大.当λ由0 增至2 时，桩顶水平位移由0.71 增至1，增加了40.85%；桩身最大弯矩值由0.56 增至1，提高了78.57%.2）竖向荷载特征参数λ的变化在较浅深度范围内（z=0～0.4L）对桩身无量纲位移影响显著，而随着深度的增加，这种影响逐渐减缓，下半段桩身位移曲线基本重合.桩身无量纲弯矩在距桩顶L/3深度位置出现反转拐点，而桩身最大位移和最大弯矩发生位置受竖向荷载特征参数λ的影响较小.上述计算实例进一步表明，桩顶竖向荷载和水平荷载引起的P-Δ 效应会影响桩身最大水平位移和弯矩，可能威胁结构的安全，在工程设计计算中应引起重视.

图12 不同竖向荷载作用的桩身无量纲水平位移对比图Fig.12 Comparison of dimensionless lateral displacement of the pile under different vertical loads

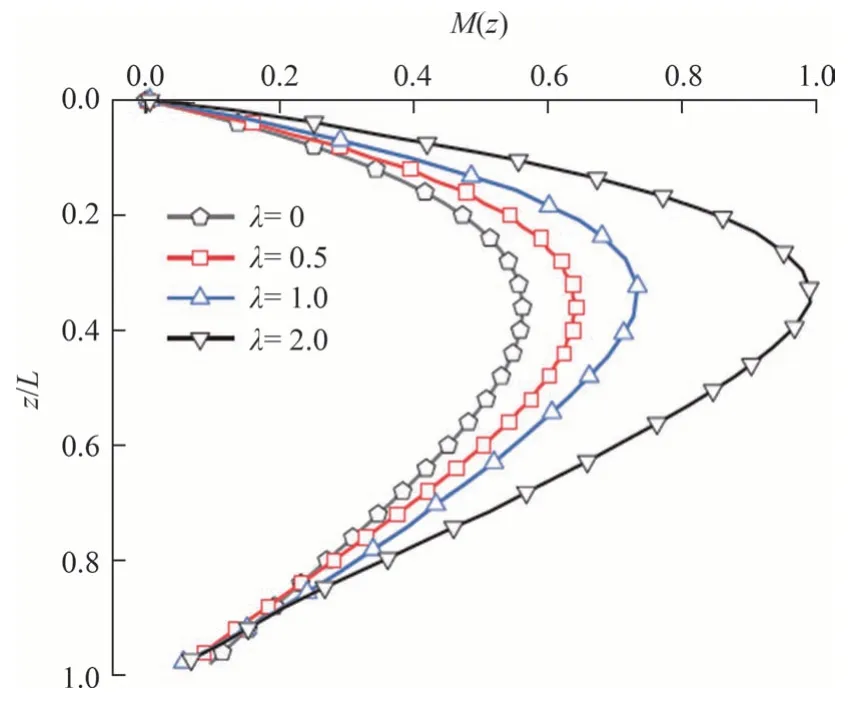
图13 不同竖向荷载作用的桩身无量纲弯矩对比图Fig.13 Comparison of dimensionless bending moment of the pile under different vertical loads

5.3 水平简谐荷载幅值H0的影响

赵明华等［30］结合水平受荷桩模型试验，认为桩顶水平位移x=0.15dp时的荷载近似等于桩基的水平极限承载力Hu.结合算例，求得其水平极限承载力为Hu=1 100 kN.为探究不同水平简谐荷载幅值H0对桩身内力和变形的影响，图14和图15给出了水平简谐荷载幅值H0分别为0.2Hu、0.4Hu、0.8Hu和1.0Hu时的桩身无量纲水平位移、弯矩随深度的变化，其中P0=100 kN，其他计算参数同上.由图14、图15 可知：1）随着桩顶水平简谐荷载幅值H0的逐渐增加，桩身无量纲水平位移和弯矩均显著增大.当H0由0.2H0增至1.0H0时，桩身最大无量纲位移和弯矩值均由0.2 增至1，提高了4 倍.2）桩身位移随深度的增加呈现减小趋势，且桩身最大位移出现在桩顶；桩身弯矩随深度的增加呈现出先增加后减小趋势，最大弯矩发生位置在距桩顶2.8dp处.而桩身最大位移和最大弯矩发生位置受水平简谐荷载幅值H0的影响较小.

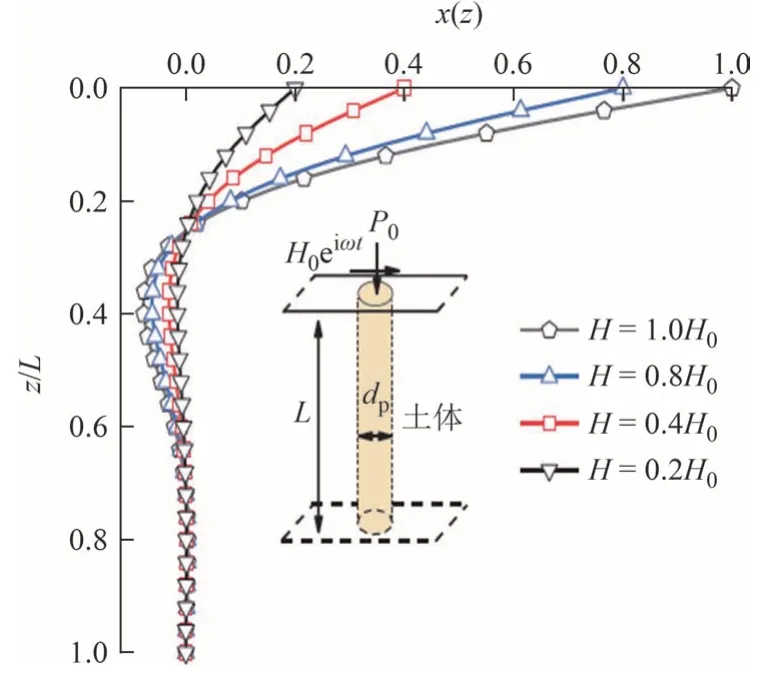
图14 不同水平简谐荷载幅值作用的桩身无量纲水平位移对比图Fig.14 Comparison of dimensionless lateral displacement of the pile under different horizontal harmonic load amplitudes

图15 不同水平简谐荷载幅值作用的桩身无量纲弯矩对比图Fig.15 Comparison of dimensionless bending moment of the pile under different horizontal harmonic load amplitudes

5.4 水平简谐荷载无量纲频率a0的影响

图16、图17 给出了桩身长径比L/dp为10 和30，无量纲激振频率a0=0.01、0.5 和1.0 时［28］桩身无量纲水平位移、弯矩随深度的变化.由图16和图17可知：1）在不同桩身长径比的情况下，随着a0降低，桩身最大水平位移、弯矩均逐渐增大.其中，当L/dp=10 和30，a0由1.0 降至0.01 时，桩身最大水平位移分别提高105.89% 和141.67%，桩身最大弯矩分别增加15.07%和22.45%.表明桩身水平位移和弯矩受无量纲频率a0的影响较大，这是由于频率越高，桩的变形还未来得及发生，荷载已反向施加［28］，从而造成位移量和弯矩减小，因此低频振动环境对桩身内力和位移的影响更大.2）不同长径比下的桩身最大无量纲位移、弯矩发生的位置与无量纲频率a0基本无关，最大位移均位于桩顶，最大弯矩均在距地面z=3dp深度处.

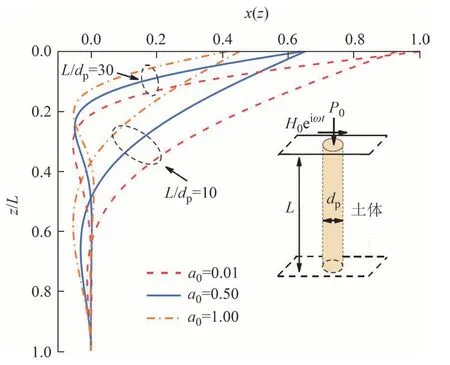
图16 不同长径比下桩身无量纲水平位移随a0的变化对比图Fig.16 Comparison of dimensionless lateral displacement of the pile with a0 under different slenderness ratios L/dp

图17 不同长径比下桩身无量纲弯矩随a0的变化对比图Fig.17 Comparison of dimensionless bending moment of the pile with a0 under different slenderness ratios L/dp

5.5 长径比L/dp的影响

图18 和图19 分析了桩身长径比L/dp分别取5、10、20和40四种情况下［7］，桩身无量纲水平位移与弯矩随深度的变化曲线，其中纵坐标归一化深度取z与最大桩长Lmax的比值（Lmax取40dp）.从图18、图19中可以看出：1）当桩身长径比较小时（L/dp=5），桩身水平位移随深度增加而减小，而桩身弯矩随深度增加而增大，且桩底弯矩最大，桩呈刚性短桩特性.2）随着长径比的增大（L/dp=10，20，40），桩身出现挠曲变形，水平位移呈曲线，桩表现为弹性长桩特性，桩身弯矩随深度先增加后减小，最大弯矩均出现在z/Lmax=0.07～0.08 处，且最大弯矩位置不随L/dp改变而变化.3）当z/Lmax≥0.5（Lp=20dp），桩身的位移和弯矩均接近于0，故可将z=20dp=Lp视为桩的有效长度，若再增加桩长（Lp=20dp，40dp），桩身水平位移、弯矩曲线已基本重合，不再随桩长的增加而变化.

图18 不同长径比下桩身无量纲水平位移对比图Fig.18 Comparison of dimensionless lateral displacement of the pile under different slenderness ratios L/dp

图19 不同长径比下桩身无量纲弯矩对比图Fig.19 Comparison of dimensionless bending moment of the pile under different slenderness ratios L/dp

6 结论

本文基于Pasternak 地基和Euler梁理论，建立了桩-土相互作用水平振动简化分析模型，考虑了竖向荷载和水平简谐荷载引起的P-Δ 效应、土体剪切效应的影响，采用改进的有限杆单元方法求解综合刚度矩阵方程，结合桩土连续边界条件得到了桩身内力和位移解答.并对土体剪切效应、桩顶竖向荷载P0、水平简谐荷载幅值H0、无量纲频率a0和桩身长径比L/dp进行参数分析，得到如下结论：

1）本文所采用的有限杆单元法通过构造桩基的整体刚度方程可综合考虑地基土体剪切效应和竖向荷载变化的影响，所得结果均与已有文献解进行对比验证.相较传统求解方法可以更简便地考虑复杂荷载、地层和边界条件的影响，计算效率高，可为进一步分析复杂工况下桩基的水平振动响应分析和设计提供参考.

2）采用Pasternak 地基模型计算得到的桩身水平位移和弯矩均小于Winkler 地基所得结果，说明未引入土体剪切模量Gs将忽略地基土体的剪切效应，使得桩体结构的受力计算结果较实际偏大.当Gs由0增至5Gs时，桩身最大水平位移和弯矩分别减小40.42%和64.27%.且随着桩土弹模比Ep/Es的降低，两种地基模型计算的桩身最大水平位移和弯矩的差异性呈现出增强趋势.

3）随着桩顶竖向荷载的增加，桩身水平位移和弯矩受P-Δ 效应的影响显著.随着桩顶竖向荷载特征参数λ的增大，桩身最大水平位移和弯矩均显著增加，其中当λ由0 增至2 时，桩身最大无量纲水平位移由0.71 增至1，增加40.85%；桩身最大无量纲弯矩由0.56增至1，提高78.57%.因此，在工程设计计算中应重视P-Δ 效应对桩身内力和变形的影响，避免威胁结构的安全.

4）整体上，桩身长径比L/dp对有限长桩的位移、弯矩的动力响应影响较大；当桩长L＞20dp后（无限长桩），影响逐渐减小.且桩基础的水平动力响应随着水平简谐荷载幅值H0的增加而增加，随着无量纲频率a0的降低而增加.其中H0由0.2H0增至1.0H0时，桩身最大无量纲水平位移和弯矩均提高了4倍；当L/dp=30，a0由1.0 降至0.01 时，桩身最大无量纲水平位移和弯矩分别提高了141.67%和22.45%.故在工程设计中应注重水平简谐荷载高幅值、低频率振动环境对桩身变形和内力的影响.