基于不同失稳判据的黄土边坡稳定性数值计算分析
2024-03-31王昕宇钟佩文张慧莉陈卓田堪良
王昕宇 钟佩文 张慧莉 陈卓 田堪良


摘 要:安全系数是边坡稳定性评价的一项重要指标,依据不同失稳判据计算得到的安全系数存在差异,会直接影响边坡稳定性状态的评价。以万花山治沟造地工程台阶型开挖边坡为对象,运用FLAC3D 有限差分软件,采用强度折减法,选择计算不收敛判据、塑性区贯通判据、位移突变判据3 种失稳判据,对黄土边坡安全系数进行数值计算。对比分析3 种判据所得的分析结果及优缺点表明:3 种失稳判据得出的安全系数大小排序为位移突变判据>计算不收敛判据>塑性区贯通判据。计算不收敛判据使用简便,求解快速,但不能展示折减过程坡体塑性区的变化情况;塑性区贯通判据不宜单独作为边坡失稳判据,需要结合不平衡力综合评估,但可以展示坡体剪切和拉伸塑性区;位移突变判据求解过程复杂,但能真实地反映坡体位移变化导致的临界破坏状态。建议类似工程优先选用求解过程快速的计算不收敛判据,然后结合塑性区贯通情况与坡体位移变化状态对边坡稳定性进行综合评价。
关键词:黄土边坡;失稳判据;安全系数;强度折减法;稳定性分析
中图分类号:TV223.6;TU457 文献标志码:A doi:10.3969/ j.issn.1000-1379.2024.03.026
引用格式:王昕宇,钟佩文,张慧莉,等.基于不同失稳判据的黄土边坡稳定性数值计算分析[J].人民黄河,2024,46(3):143-147,155.
强度折减法提出后在边坡稳定性分析方面得到了广泛应用[1-3] 。基于强度折减法得到的安全系数往往依赖于失稳判据的选择[4] 。边坡失稳判据主要有计算不收敛判据、塑性区贯通判据、位移突变判据3种[5] 。目前对于边坡失稳判据尚未达成共识,导致不同研究人员针对同一个边坡得出的安全系数有很大差异[6-8] 。边坡稳定性研究需要结合实际工况进行分析,针对实际工况选用何种失稳判据得出的安全系数更为可靠,一直是学界研究的热点。王其宽等[9] 基于3 种不同失稳判据,针对露天矿山堆载边坡的特殊情况研究得出,计算不收敛判据对应的安全系数较大,位移突变判据对应的安全系数较小,需要结合3 种判据所得结果综合评价露天矿山边坡的稳定性。陈林杰等[10] 通过对地铁车站隧道交叉段的土体进行稳定性研究,得出采用位移突变判据与塑性区贯通判据相结合的方法,可以较准确地得到工况的安全系数。王鹏等[11] 采用3 种失稳判据对贵州仁遵某在建公路桥梁岸坡进行稳定性分析,收敛性判据得到的安全系数最大,塑性区贯通判据次之,位移突变性判据所得结果最小,宜以位移突变性判据进行稳定性分析。郝进锋等[12] 研究单洞室稳定性,得出单洞室塑性区围绕开挖面存在,计算不收敛判据所得安全系数比位移突变判据的大,塑性区贯通判据所得安全系数比位移突变判据的小,宜采用位移突变判据求解安全系数。邵冠慧等[13] 总结分析国内外对于隧道稳定性的判别方法后,得出对于不同的地质条件,失稳判据的选择有所不同。
综合上述研究发现,在失稳判据选择方面,针对不同的实际工况,学者进行了大量的研究,然而,目前采用3 种失稳判据对黄土边坡进行稳定性分析的研究还比较少。近年来,发轫于延安的治沟造地工程,是针对黄土高原区特殊的丘陵沟壑地貌启动的一项治沟保生态、造地惠民生的系统工程[14] 。但在工程实施过程中,会形成大量裸露的黄土邊坡,这些边坡在遇到工程切坡以及坡顶荷载超载等情况时会发生失稳,从而导致滑坡的发生[15] 。因此,针对黄土边坡,选择何种失稳判据进行稳定分析就显得尤为重要。
FLAC3D 有限差分软件以单元格为基本单元展示模拟材料的剪切、拉伸破坏情况,在模拟岩体材料的受力破坏和变形方面应用广泛[16] 。因此,本研究选用FLAC3D 有限差分软件,根据陕北黄土高原区万花山治沟造地工程中台阶型开挖边坡的实际情况建立几何模型,采用3 种失稳判据,逐一对黄土边坡稳定性进行数值计算,对比分析3 种判据评价结果的差异及优缺点,为实际工况中黄土边坡稳定性评价提供技术方法。
1 参数选取与模型建立
1.1 参数选取
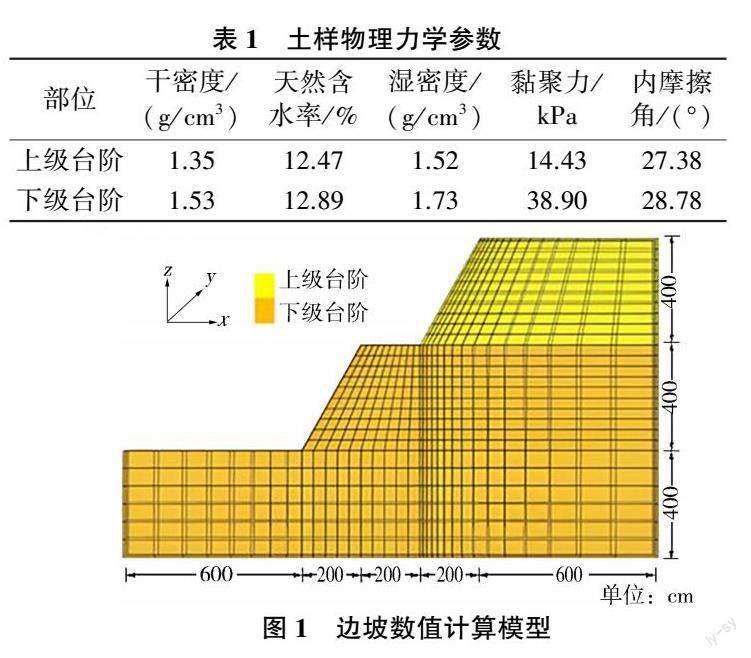
试验所用土样采自陕西省延安市万花山,是当地治沟造地工程中涉及的主要土壤,模型建立所需边坡土样的物理力学参数取自钟佩文等[17] 2016 年5 月1日至7 月10 日试验结果,见表1,土样属湿陷性(Q3 )黄土。
1.2 模型建立
以万花山治沟造地工程中两级台阶的边坡尺寸为依据,建立黄土边坡数值计算模型,如图1 所示。单极坡高4 m,边坡高8 m,单极坡比1 ∶ 0.5,两级中间为2 m宽的平台。基于Mohr-Coulomb 强度理论,利用FLAC3D 软件进行数值分析。模型的底部和四周均采用固定边界来模拟半无限场地,其中左右边界固定x方向,前后边界固定y 方向,底部固定z 方向。
2 强度折减法
2.1 计算原理
利用FLAC3D 有限差分软件,采用强度折减法计算边坡安全系数。具体计算方法为:利用折减系数F ,对土体的黏聚力c 和内摩擦角φ 进行折减,当达到失稳判据的条件时,边坡处于临界失稳状态,此时原始黏聚力与折减后临界破坏时黏聚力的比值即为安全系数。强度折减法基本公式为[18]
cF = c0 / F (1)
tan φF = tan φ0 / F (2)
式中: F 为折减系数, c0 为折减前的黏聚力, φ0 为折减前的内摩擦角, cF 、φF 分别为边坡到达临界破坏状态时的黏聚力和内摩擦角。
2.2 边坡失稳判据
1)计算不收敛判据。边坡失稳破坏时,滑动区土体发生滑动并无限发展,这种状态下,滑移面上的塑性位移会发生突变,在力的收敛标准和位移的收敛标准下,程序的求解结果均不收敛,因此可以把数值计算结果是否收敛作为判别边坡失稳的依据。
2)塑性区贯通判据。采用强度折减法计算安全系数时,边坡内部土体受应力作用逐渐发生塑性破坏,塑性区从坡脚发展到坡顶的过程,坡体内部会产生不同程度的塑性变形,塑性区贯通时,边坡处于临界失稳状态。
3)位移突变判据。边坡内部土体受应力作用发生剪切破坏时,边坡部分土体会发生略微移动,边坡达到临界失稳状态时,部分土体的位移量会突增,通过在边坡内部设置位移监测点,观察位移变化,从而判断边坡是否失稳。
3 自然状态边坡稳定性分析
3.1 计算不收敛判据结果分析
调用slove fos 命令使用内置模块对边坡模型进行分析,采用强度折减法求解安全系数,得出的剪切应变增量云图见图2。发生剪切应变的区域主要在上级台阶,剪切应变增量为0.003 0~0.012 3,应变带呈圆弧状从坡脚逐渐向坡顶方向发展,最大剪切应变增量发生在坡脚处,为0.012 3,产生局部塑性变形,从而导致上级边坡存有潜在塑性贯通区域,此区域受土体自重的影响,有发展为滑移面的可能。依据计算不收敛判据,此时的折减系数即安全系数,数值为1.953 1。
3.2 塑性区贯通判据结果分析
采用强度折剪法计算边坡的安全系数时可以展示剪切塑性区和拉伸塑性区的状态。通过FLAC3D 软件得到的折减系数在1.700 0~2.000 0 范围内坡体塑性区贯通情况如图3 所示。对于剪切塑性区,软件输出结果中以shear-n 标识的区域土体正处于破坏状态,以shear-p 标识的区域土体在折减过程中曾进入过破坏状态,但此时已退出;对于拉伸塑性区,软件输出结果中相应土体状态则分别以tension-n 与tension-p 标识。当处于破坏状态的区域贯通时,贯通区上方的土体单元会因自重作用而形成滑动带,此时边坡处于临界失稳状态。
折减系数为1.700 0 时上级台阶的坡脚处出现剪切塑性区,折减系数增大至1.800 0 的过程中,剪切塑性区不断向坡顶发展,剪切塑性区下方为退出破坏状态区域、上方为处于破坏状态区域,这表明随着折减系数的增大,剪切应力主要集中在该区域上部,从而产生土体局部塑性变形并向上发展。折减系数增大至1.850 0时,图3(c)上级台阶上部出现拉伸塑性区ten?sion-n,表明此区域正出现拉应力集中,边坡塑性区即将贯通。折减系数为1.895 0 时,图3(f)拉伸塑性区tension-n 恰好贯通,该判据下临界折减系数1.895 0即安全系数。随着折减系数的继续增大,贯通区域扩大,当折减系数增大至1.950 0 时,边坡靠近临空面部分开始出现拉伸塑性区tension-p,表明该区域曾处于破坏状态。这说明随着塑性贯通区域的继续扩大,边坡靠近临空面部分受贯通区域拉伸破坏力以及土体自重的影响开始出现滑坡前兆,当滑坡发生时,这部分土体脱离边坡整体,所受拉伸破坏力消失。通过观察不同折减系数的塑性区贯通情况发现,塑性区主要在上级台阶左部,下级台阶无塑性区,稳定性好。实际情况中,底部不会出现大量剪切塑性区,原因是底部为固定约束,存在边界效应[19] 。
3.3 位移突变判据结果分析
通过FLAC3D 软件中FISH 语言工具在边坡关键位置设置监测点,绘制不同折减系数的位移变化曲线,从而找到位移突变点,得到边坡安全系数。
依据位移突变判据,坡体x 方向位移云图及潜在滑移面如图4 所示,滑移线左侧靠近临空面部分有不同程度x 方向的位移,滑移线右侧位移小于0.01 mm。依据图4 边坡x 方向位移变化情况,在边坡上级台阶及下级台阶设置监测点P01~P12(部分监测点布设位置见图4),可以得到不同折减系数的监测点位移(部分结果见表2,负號代表x 轴负方向,即临空面方向),可绘制位移变化曲线。
通过观察监测点的位移变化情况发现:折减系数大于1.953 1 时,P05、P06、P11、P12 监测点的位移有明显变化,折减系数增至1.968 8 时,P05 监测点位移从-12.934 0 mm 增至-89.220 0 mm,P06 监测点位移从-11.888 0 mm 增至-84.283 0 mm,P11 监测点位移从-12.009 0 mm 增至82.326 0 mm,P12 监测点位移从-11.929 0 mm 增至-83.478 0 mm;其余监测点位移在整个过程中没有发生明显变化,说明所在部位稳定性较好。此方法得到的安全系数选取1.953 1 和1.957 0的中间值1.955 1。
3.4 3 种判据所得安全系数差异分析
计算不收敛判据、塑性区贯通判据、位移突变判据得到的安全系数分别为1.953 1、1.895 0、1.955 1。位移突变判据与计算不收敛判据结果接近,差值仅为0.002 0,塑性区贯通判据结果偏小,与位移突变判据和计算不收敛判据差值分别为0.060 1、0.058 1。
当不平衡力计算结果趋于一个非零值时可认为发生塑性变形。因此,使用FLAC3D 软件对折减过程中边坡模型不平衡力进行计算,分析边坡失稳过程中塑性区的变化状态,如图5 所示。
由图5(a)和图5(b)可以看出,随计算时步逐渐增加,不平衡力逐渐减小最后趋于零,这表明在折减系数为1.895 0 和1.900 0 时,边坡处于稳定状态。但在塑性区贯通判据下,折减系数为1.900 0 时(大于安全系数1.895 0),边坡已经失稳,此时塑性区贯通判据所得结果不准确。原因是塑性区贯通后,其附近的土体受边界条件限制而阻止塑性区继续发展,边坡未达到临界失稳状态。由图5(c) 可知折减系数为1.950 0时,不平衡力随着计算时步增长逐渐减小,最后趋于一个非零值,说明边坡已经发生塑性变形,且依据塑性区贯通判据,边坡同样为失稳状态,此时塑性区贯通判据所得结果准确。结合图3(h)塑性区贯通情况,在边坡模型上级台阶处,上方遍布正处于破坏状态的拉伸塑性区tension-n,而靠近台阶边缘处充满已经退出破坏状态的拉伸塑性区tension-p,此区域曾进入过破坏状态,受力的影响已经变为滑动带,边坡失稳,图5(c)平衡力在后期略微起伏并趋于一个非零值,此时边坡才真正发生临界失稳。折减系数为1.980 时,随着计算时步的增长,不平衡力后期产生明显波动,表明其不满足不平衡力求解要求。可见,塑性区贯通不宜单独作为边坡失稳的判据,其会出现判断结果偏小的情况,需要结合不平衡力综合分析边坡安全系数。综合分析得到安全系数为1.950 0,与计算不收敛判据、塑性区贯通判据所得结果的差值分别为0.003 1 与0.005 1,差值明显缩小。
由3 种判据计算结果可以看出:数值收敛判据直接调用软件内置模块对边坡进行稳定性分析,使用简便,计算快速,但不能展示随着折减系数的增大,坡体塑性区的变化情况。塑性区贯通判据得到的安全系数偏小,不够真实准确,原因是塑性区贯通是边坡失稳破坏的必要条件,而不是充分条件[20] ,此判据只能模拟土的强度特性,不能模拟实际应力—应变关系[21] ,需要结合不同折减系数的不平衡力进行综合分析,但通过图3 可得到随着折减系数的增大整个边坡潜在的破坏区域分布以及滑动面相对位置,在这方面此判据优于其他两个判据[22-23] 。位移突变判据得到的安全系数与计算不收敛判据所得结果接近,需要在边坡关键位置设置监测点,过程复杂,但能够根据坡体位移变化情况真实反映边坡的临界破坏状态[24] 。
4 结论
1)基于不同失稳判据对黄土边坡稳定性进行分析,所得安全系数由大到小排序为:位移突变判据1.955 1,计算不收敛判据1.953 1,塑性区贯通判据1.895 0。位移突变判据与计算不收敛判据结果接近,差值仅为0.002 0,塑性区贯通判据所得结果偏小,与位移突变判据和计算不收敛判据差值分别为0.060 1、0.058 1。
2)计算不收敛判据直接调用软件内置模块进行边坡稳定性分析,使用简便,计算快速,但不展示折减过程坡体塑性区的变化情况。塑性区贯通判据所得安全系数较小,原因是塑性区贯通时边坡未必处于临界失稳状态,不宜单独作为边坡失稳判据,需要结合不平衡力综合评估,但此判据可以展示随着折减系数的增大坡体的剪切和拉伸塑性区变化情况。位移突变判据分析需要在边坡关键位置设置监测点,求解过程复杂,但能分析坡体位移变化状态。
3)在实际工况中,针对类似万花山治沟造地工程开挖的台阶型黄土边坡,建议优先选用求解简便、快速的计算不收敛判据进行稳定性分析、得到安全系数,并且参考其他判据得到的塑性区贯通情况与坡体位移变化状态,以准确分析黄土边坡稳定性状态。
参考文献:
[1] 史俊涛,孔思丽,任琪.有限元强度折减法边坡失稳判据适用性分析[J].人民黄河,2014,36(2):135-137,140.
[2] 牛越先,马俊.土质边坡稳定性影响因素的研究[J].水土保持研究,2011,18(4):273-276.
[3] NAEIJ M,GHASEMI H,GHAFARIAN D,et al.Explicit FiniteElement Analysis of Slope Stability by Strength Reduction[J].Geomechanics and Engineering,2021,26(2):133-146.
[4] 李永亮,周国胜,李永鹏.有限元强度折减法边坡失稳判据的适用性研究[J].水利与建筑工程学报,2018,16(5):125-129.
[5] 陶宇,梁伟桥,谢卫兵.有限元强度折减法分析边坡稳定性的判据研究[J].工业建筑,2019,49(2):103-106.
6] DONG J,WANG C,HUANG Z,et al.Dynamic Response Charac? teristics and Instability Criteria of a Slope with a MiddleLocked Segment[J]. Soil Dynamics and Earthquake Engi? neering,2021,150:106899.
[7] 贺俊,史俊涛,黄璐,等.强度折减法中非均质层状土坡失稳判据适用性[J].人民黄河,2014,36(12):122-125.
[8] 安光明,刘大安,郑书彦,等.涪陵区植物油厂滑坡有限元强度折减分析[J].水土保持研究,2009,16(1):175-178.
[9] 王其宽,梁世春,宋晓雷.基于不同失稳判据的堆载边坡稳定性分析[J].现代矿业,2021,37(6):110-114.
[10] 陈林杰,梁波.基于强度折减法的地铁车站交叉段稳定性分析[J].地下空间与工程学报,2018,14(1):260-265.
[11] 王鹏,谭明建,谢尚铕,等.贵州仁遵高速公路某特大桥岸坡稳定性分析[J].四川建材,2022,48(8):167-170.
[12] 郝进锋,刘明宾.强度折减法在单洞室稳定性分析中的失稳判据比较[J].城市建筑,2022,19(2):102-105.
[13] 邵冠慧,李晓昭,赵晓豹,等.不同变形失稳模式下隧道围岩稳定性判据研究的进展[J].防灾减灾工程学报,2009,29(5):577-582.
[14] 王健,肖鹏.富县:治沟造地“保生态”“惠民生”[J].西部大开发,2019(7):106-107.
[15] BRUSCHI V M,BONACHEA J,REMONDO J,et al.Analysis ofGeomorphic SystemsResponse to Natural and Human Driversin Northern Spain: Implications for Global GeomorphicChange[J].Geomorphology,2013,196(7):267-279.
[16] 赵岳然.基于FLAC3D 的余吾矿高抽巷合理层位研究及应用[J].能源技术与管理,2019,44(6):38-40.
[17] 钟佩文,张慧莉,田堪良,等.持续降雨入渗对黄土边坡稳定性的影响[J].人民黄河,2018,40(1):76-81.
[18] ZIENKIEWICZ O C,HUMPHESON C,LEWIS R J G.Asso?ciated and Non?Associated Visco?Plasticity and Plasticity inSoil Mechanics[J].Géotechnique,1975,25(4):671-689.
[19] 张爱军,莫海鸿.有限元强度折减法中边坡失稳位移突变判据的改进[J].岩土力学,2013,34(增刊2):332-337.
[20] 李垠,程丹,苏凯.基于有限元强度折减法的边坡失稳判据统一性研究[J].大地测量与地球动力学,2016,36(1):69-74.
[21] 牛志力.软基高填路堤沉降及边坡强度折减稳定性分析[J].筑路机械与施工机械化,2009,26(4):54-56.
[22] 趙尚毅,郑颖人,张玉芳.极限分析有限元法讲座:Ⅱ有限元强度折减法中边坡失稳的判据探讨[J].岩土力学,2005,26(2):332-336.
[23] 赵尚毅,时卫民,郑颖人.边坡稳定性分析的有限元法[J].地下空间,2001,7(增刊1):450-454,589.
[24] 廖少波.基于位移突变判据的岩质边坡动力稳定性研究[J].地下空间与工程学报,2017,13(增刊2):921-925.
【责任编辑 张华岩】
