轿车子午线轮胎侧向松弛长度的仿真分析
2024-03-29宋美芹邢正涛翟明荣孟照宏史彩霞于成龙
宋美芹,邢正涛,翟明荣,孟照宏,史彩霞,于成龙
(1.青岛轮云设计研究院有限责任公司,山东 青岛 266400;2.青岛双星轮胎工业有限公司,山东 青岛 266400)
轮胎为车辆与地面接触的唯一部件,影响车辆的操纵稳定性、行驶平顺性和安全性等。轮胎的瞬态效应主要包括轮胎松弛长度、惯性和陀螺效应,是车辆操纵稳定性的主要评价指标之一[1-6]。轮胎松弛长度是轮胎表征瞬态特性的主要指标,反映了轮胎输入力与输出位移响应之间的时间延迟特性,即当车辆出现瞬态转向时,轮胎驱动轮辋随方向盘转动一定角度(此时轮胎承受侧向力),由于轮胎结构的复杂性及胶料的粘弹性,在一段时间后,轮胎才与轮辋转向角度一致,侧向力达到稳定。从轮胎引入转向角到其侧向力达到稳定所需的时间为轮胎松弛时间,轮胎在侧向力达到其63.2%稳定值的时间内滚动的距离为轮胎松弛长度。
轮胎松弛包括侧向松弛和纵向松弛两种,前者影响车辆的操纵稳定性,后者影响车辆的制动性能。轮胎松弛长度(或松弛时间)越短,轮胎的操控性能越优异。因此,准确预测轮胎松弛长度对精确模拟车辆转向响应具有重要的意义[7]。
从20世纪50年代起,人们开始探索研究轮胎松弛长度,轮胎松弛特性的作用机理、分析模型(包括刷子模型、弦模型和非稳态模型等)、试验方法和表征方法等已有文献报道[8-9]。V.V.VANTSEVICH等[10]对之前文献中的轮胎侧向和纵向松弛长度进行了统计分析。W.LUTY[11]运用基本松弛模型对轮胎侧向松弛长度进行仿真分析,得到了轮胎转角变化对侧向力的影响规律。C. F. WEI等[7]采用有限元方法,研究了轮胎材料和结构特性对轮胎松弛长度的影响。李飞等[12-13]采用不同的测试方法对轮胎侧向松弛长度进行了研究,得出测试方法对轮胎松弛长度的影响。
在轮胎松弛长度的有限元仿真中,边界条件设定方法有两种,一种是对轮胎与轮辋同时施加瞬时侧偏角(简称方法1),另一种是仅对轮辋施加瞬时侧偏角(简称方法2)。
本工作以215/60R17 96H DH16S轿车子午线轮胎为研究对象,通过建立复杂花纹轮胎的三维有限元模型,分析不同轮胎侧向松弛长度的仿真实现方法,并借助六分力试验机对轮胎侧向松弛长度进行了验证,可为轮胎动力学数字化模型的快速构建提供参考。
1 有限元仿真
1.1 材料模型
橡胶材料具有非线性的力学性能,目前常用的材料模型有Neo-Hookean模型、Yeoh模型、Mooney-Rivlin模型及Ogden模型,主要表征橡胶材料的超弹和粘弹特性,同时在表征其粘弹特性时也会用到Prony级数、时温等效方程和松弛参数等。
1.2 结构模型
轮胎有限元建模流程如图1所示。
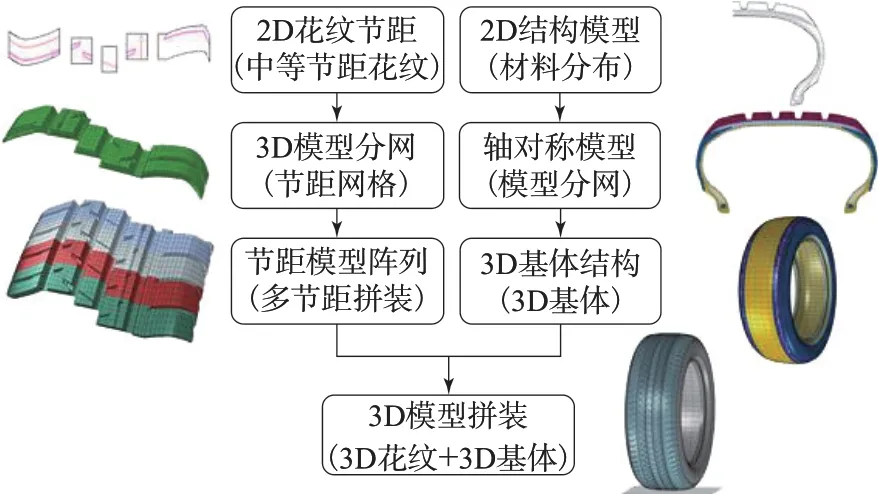
图1 轮胎有限元建模流程
轮胎的有限元模型分为胎体和胎面花纹两部分,具体建模步骤见文献[14]。
轮胎侧向松弛长度的测试条件为:充气压力230 kPa,标准负荷 5 000 N,侧偏角 1°,速度5 km·h-1;考虑到仿真计算的时效问题,仿真速度设定为60 km·h-1,其他条件同测试条件。
1.3 有限元分析方法
在车辆转弯的仿真分析中,轮胎在一段时间内达到预定侧偏角,其侧向力在该段时间内从较小值增大到稳定值,不同转向输入会影响轮胎的松弛特性。在轮胎有限元仿真分析中,转向的阶跃输入(或称瞬时输入)可以采用方法1和方法2两种边界条件。方法1设定轮胎与轮辋的瞬时阶跃起始时间为0.15 s,阶跃时间为0.10 s;方法2仅对轮辋设定阶跃起始时间为0.15 s,阶跃时间为0.10 s。
在轮胎侧向松弛长度的实际试验中,无法对轮胎和轮辋同时施加侧偏力或侧偏角,只能通过对轮辋施加力或角度,然后传递给轮胎。哪种仿真方法与试验结果更加吻合,需要经过试验分析来验证。
2 轮胎侧向松弛长度测试
采用美国MTS公司生产的六分力试验机按照GMW 15204—2007《轮胎力和力矩稳态试验》和GMW 15206—2007《轮胎残余回正力矩试验》测试试验轮胎的力学性能,测试条件为:温度25 ℃,数据采集频率 1 024 Hz。
轮胎侧向松弛长度的测试方法主要有刚度法、侧偏角阶跃法(先施加侧偏角,再施加测试速度)和转动角阶跃法(先施加测试速度,再施加侧偏角),其中侧偏角阶跃法包括先转角后加载法和先加载后转角法[2]。
为实现仿真分析与试验过程的一致性,本工作采用转动角阶跃法[13],具体步骤如表1所示。
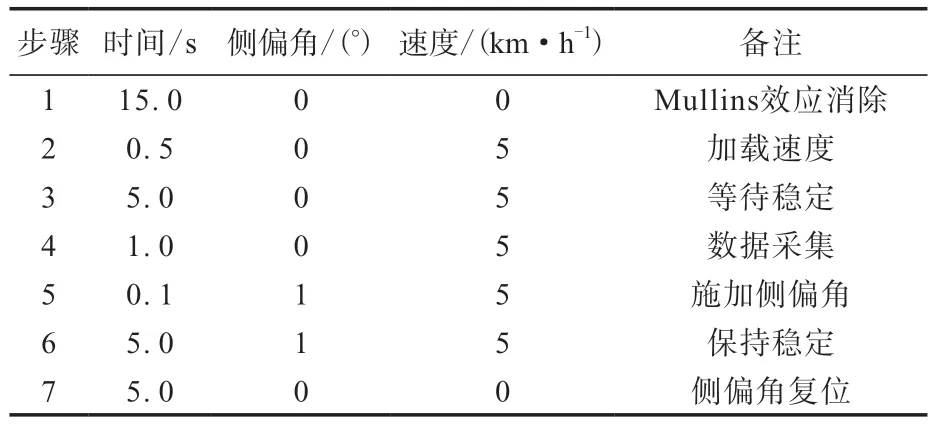
表1 转动角阶跃法测试要求
3 计算原理
在轮胎松弛长度仿真与试验数据的分析中,为方便计算输出结果,可将其分解为无限多个小阶跃步,通过小阶跃步将所有结果相加,得到总结果,然后通过优化迭代得到最优解。
轮胎侧向力表达式为
式中:F为轮胎侧向力,N;FSS为轮胎达到稳定时的侧向力,N;t为时间,s;β为轮胎松弛时间,s。对小阶跃步进行卷积积分,有
式中,τ为小阶跃的时间,s;AT为小阶跃步长。
当轮胎达到稳定时,t=β,此时阶跃侧向力与侧向松弛长度分别为
式中:F63.2%为稳态侧向力的63.2%;v为轮胎速度,m·s-1;l为轮胎侧向松弛长度,m。
4 结果与讨论
4.1 不同仿真方法对轮胎侧向松弛长度的影响
不同方法下,轮胎侧向力随时间变化的仿真及拟合曲线如图2所示。
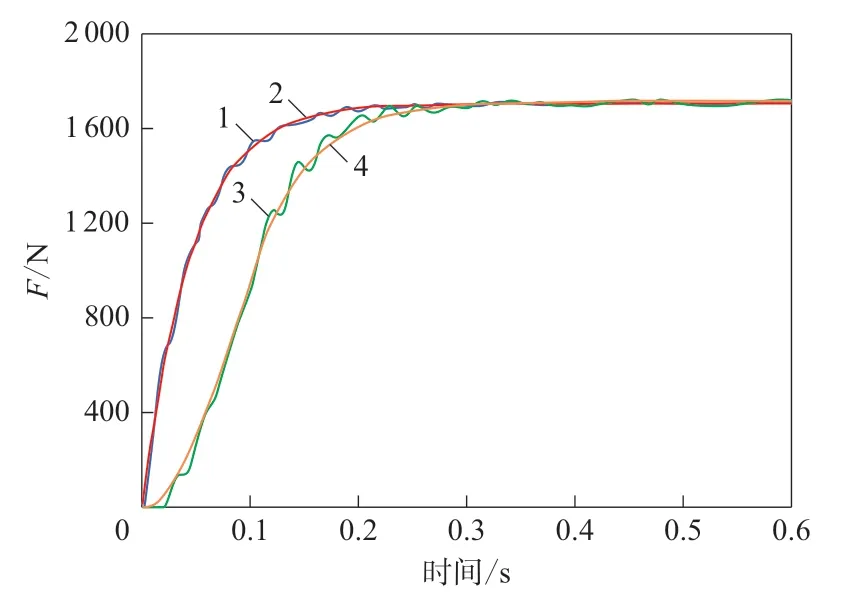
图2 轮胎侧向力随时间变化的仿真及拟合曲线
从图2可以看出,在相同充气压力、负荷和侧偏角下,通过两种方法得到的轮胎侧向力的最大值相近。但是轮胎侧向力趋于稳定的时间不同,采用方法2的轮胎侧向力趋于稳定的时间长于方法1。
不同负荷率下轮胎侧向松弛长度的仿真结果和试验结果如表2所示。
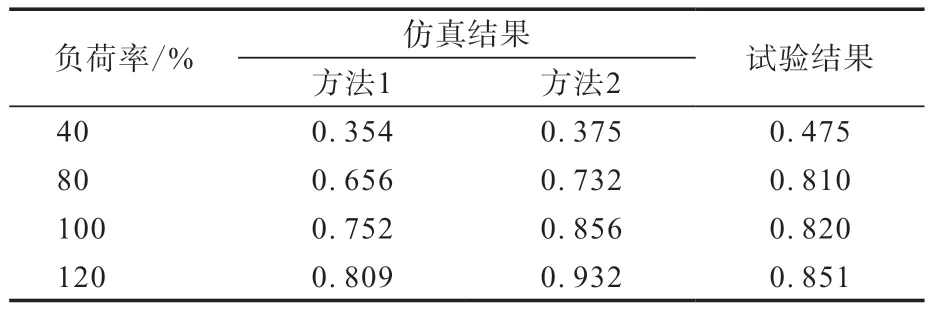
表2 不同负荷率下轮胎侧向松弛长度的仿真结果和试验结果 m
从表2可以看出:轮胎侧向松弛长度的仿真结果与试验结果均有相同的规律,即随着负荷的增大,轮胎侧向松弛长度呈增大趋势;与方法1相比,方法2仿真结果与试验结果更接近。因此采用方法2进行后续轮胎侧向松弛长度的仿真计算。
4.2 不同工况对轮胎侧向松弛长度的影响
4.2.1 负荷的影响
不同负荷率下,轮胎侧向力随时间的变化曲线如图3所示,对应的侧向松弛长度如表3所示。

表3 不同负荷率下的轮胎侧向力最大值和侧向松弛长度

图3 不同负荷率下轮胎侧向力随时间的变化曲线
从图3和表3可以看出:随着负荷率的增大,轮胎侧向力最大值增大,但是增大的幅度逐渐减小;轮胎侧向力趋于稳定的时间延长,轮胎侧向松弛长度增大。
4.2.2 充气压力的影响
不同充气压力下轮胎侧向力随时间的变化曲线如图4所示,对应的侧向松弛长度如表4所示。
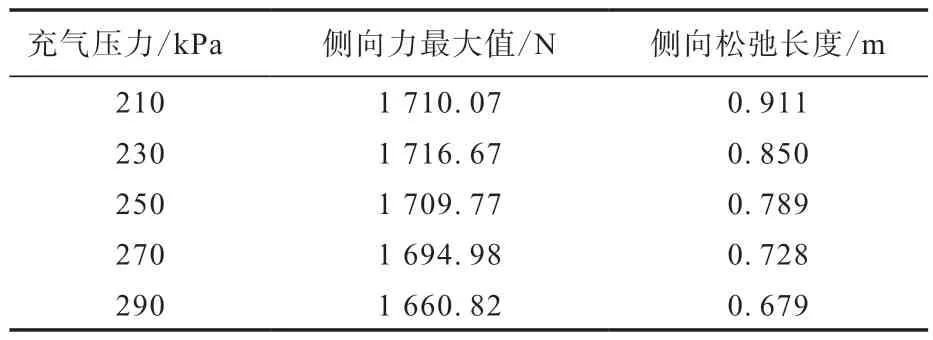
表4 不同充气压力下的轮胎侧向力最大值和侧向松弛长度
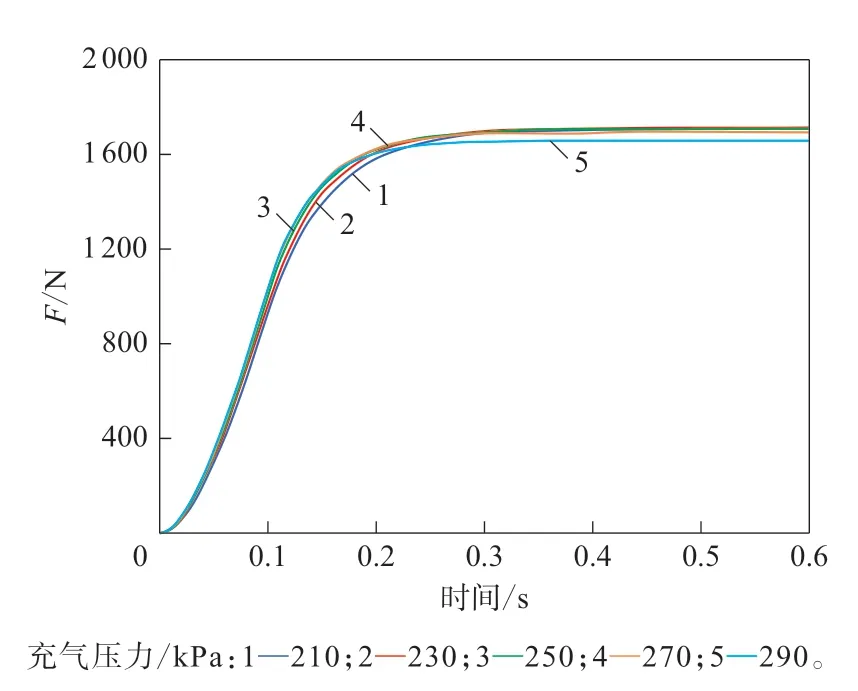
图4 不同充气压力下轮胎侧向力随时间的变化曲线
从图4和表4可以看出,随着充气压力的增大,轮胎侧向力最大值的变化很小,但轮胎侧向松弛长度呈现减小的趋势。这是因为,随着充气压力的增大,胎侧刚性增大、形变减小,轮胎与路面的接触面积减小,导致轮胎侧向松弛长度减小。
5 结论
(1)在仿真分析中,采用不同的边界设定方法可以得到不同的轮胎侧向松弛长度,与方法1相比,方法2与试验结果的吻合度更高。
(2)随着负荷的增大,轮胎侧向力的最大值和侧向松弛长度均增大。
(3)随着充气压力的增大,轮胎侧向力最大值变化不大,轮胎侧向松弛长度减小。
另外,轮胎侧向松弛长度的影响因素还有轮胎速度、侧偏角、阶跃时间以及骨架材料、胶料等,有待开展进一步的研究。
