新能源场站过电压受变压器磁饱和影响机理分析及修正方法

范 越，陈 颖，霍 超，谭镇东，董雪涛，段乃欣

（1.国家电网有限公司西北分部,陕西省西安市 710048；2.清华大学电机工程与应用电子技术系,北京市 100084；3.清华四川能源互联网研究院,四川省成都市 610042）

0 引言

近年来,中国特高压直流工程及大规模新能源基地建设保持快速增长态势,电源和电网格局发生重大变化。特高压直流工程的建设为中国西北、华北等区域新能源消纳提供了重要的外送通道。但新能源基地送端电网电力电子化特征日趋明显,电力电子发电装备数量大、控制复杂且存在多时间尺度耦合特性,新能源与直流输电的动态交互作用加剧,系统振荡呈宽频带、时变和多形态特征［1-3］。西北电网处于直流送端,在直流输电的受端发生换相失败或连续换相失败时,西北电网的新能源汇集区域存在明显的过电压现象。文献［4-5］分别研究了直驱风机和双馈风机接入电网后系统的暂态电压稳定问题,结果表明二者对系统的暂态电压稳定性均产生了不利影响。文献［6］指出高比例新能源形态下的电力系统在发生交流N-1 故障时可引发新能源群、直流群之间巨大的有功、无功波动,各系统间产生连锁反应,且大容量直流系统会恶化连锁事件的演化进程。

新能源的暂态过电压问题限制了特高压直流近区电网新能源的接入规模,增大了系统连锁故障的风险。因此,开展新能源接入端暂态过电压水平及其关键影响因素研究具有重要意义。

针对上述问题,已有工作从动态无功源配置及控制策略、新能源开机状况和风电机组暂态无功控制策略优化设计等方面展开研究,分析了故障后直流送端系统暂态过电压机理,提出了抑制暂态过电压的策略［7-9］。本文重点关注变压器磁饱和特性对新能源接入点过电压的影响。常规变压器在端电压高于一定程度时存在明显的非线性饱和及磁滞现象,此时变压器的励磁电流增大,吸收无功功率增多,进而遏制了端电压的升高,会对电网的电压水平产生较大影响。文献［10-11］描述了变压器磁饱和特性的建模方法,采用磁化曲线的拟合多项式近似表示饱和特性,所用参数通过标准开路试验获得。文献［12-13］以小斜率模型描述磁化曲线,分析了变压器无功电压随饱和程度的变化情况,提出变压器在电压较高时可用于消耗感性无功功率。上述工作表明,变压器磁饱和特性可以看作一类特殊的“过电压抑制”机制,对电力系统暂态电压稳定具有重要的影响。

目前,新能源过电压研究工作主要依靠机电暂态仿真及机电-电磁混合仿真,研究内容包括分析直流换相失败引发的新能源过电压机理及影响因素,考虑的因素有低电压穿越/高电压穿越等环节的控制策略、风电场无功补偿装置等［14-18］,但是均忽略了变压器磁饱和特性,这将影响到过电压分析结论的正确性,并会对后续的无功电压优化、无功补偿设备部署等产生进一步的影响。

为了克服上述不足,本文首先讨论了目前过电压分析存在的问题,介绍了变压器磁饱和特性的建模方法。然后,揭示了变压器磁饱和特性导致其吸收无功功率的机理,量化了过电压发生时变压器磁饱和特性对无功电压的影响程度。进一步,针对未考虑变压器饱和特性的仿真结果提出了修正方法。最后,通过西北全网电磁暂态仿真案例验证了所提出理论的正确性和修正算法的有效性。

1 目前过电压分析存在的问题

目前已有研究表明,对于含大规模新能源的直流送端系统,在换相失败、直流闭锁等故障过程中,换流站与电网之间交换的无功功率将大幅波动。直流换相失败和近区交流故障使得换流站无功功率大量盈余,同时近区大量风机进入低电压穿越,无功出力增加,两者叠加造成送端系统新能源暂态过电压问题突出,成为制约电网直流输送能力和新能源送出水平的主要因素。

在如图1 所示的小型单链测试案例中对送端新能源场站的过电压问题进行详细分析。该案例采用电磁暂态仿真建模方法构建。

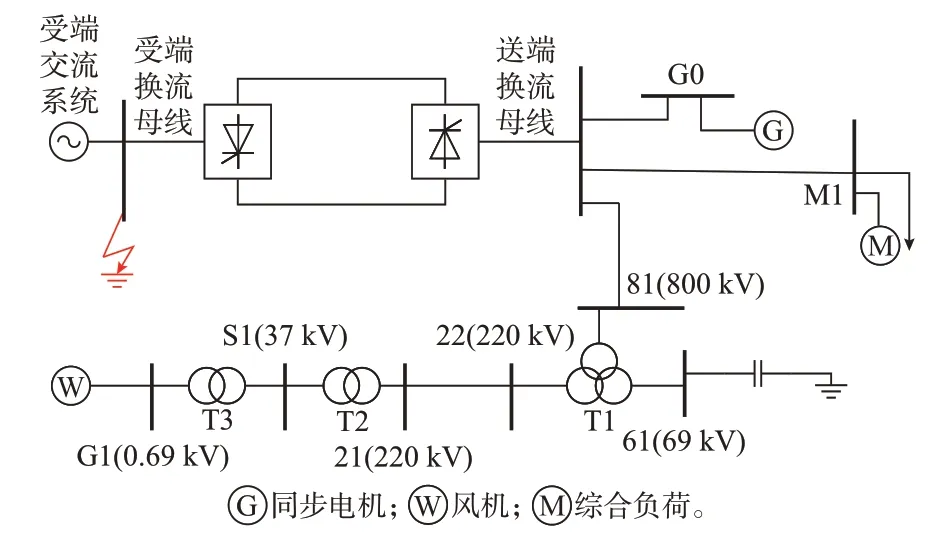
图1 过电压测试系统Fig.1 Overvoltage testing system

图1 所示系统包含800 kV 直流线、同步电机G0、风机G1,高压直流系统输送10 GW 功率,风机发电140 MW,综合负荷M1 用电200 MW,同步电机G0 发电10 079 MW。详细的发电机、直流、新能源等设备参数见附录A。设置受端换流母线在2.5 s时发生三相接地短路故障,其后0.1 s 故障切除。该故障将引发直流线受端2/4 号晶闸管出现直流换相失败现象,如附录A 图A1 所示。

在仿真中,观察到各级母线电压波动情况如附录A 图A2 所示。在各级母线中,风机接入点处的过电压最严重,达到了1.27 p.u.。

输出风机端口无功功率及低电压穿越（简称低穿）状态指示信号如附录A 图A3 所示。由图A3 可见,低电压发生后,风机进入低穿状态。在约2.7 s时,风机在低穿状态时产生了无功功率盈余。

然而,上述的计算和分析并未考虑到变压器磁饱和特性带来的影响。事实上,由于风机接入点变压器的磁饱和特性存在,在过电压发生时,变压器将会吸收无功功率,从而抑制端口过电压,即实际发生的过电压将不会达到仿真得到的1.27 p.u.。考虑变压器饱和特性与不考虑饱和特性时,风机端电压曲线如附录A 图A4 所示。风机接入点处的变压器饱和特性曲线参见附录B。

可见,不考虑变压器饱和特性时得到的过电压结果将与实际情况存在明显差异。不考虑变压器饱和特性将会影响过电压分析结果的正确性,并进一步影响暂态电压优化所需要的无功设备配置及电网的无功设备投入成本。因此,有必要研究变压器饱和特性对过电压的影响机理,量化饱和特性对过电压的影响程度,并针对已有未考虑变压器饱和特性的过电压仿真结果给出修正方法。

2 变压器磁饱和特性影响过电压机理分析

2.1 变压器及其饱和特性模型

不考虑磁饱和特性时,变压器动态方程可写为：

式中：a为变压器变比；L=L1+a2L2,其中,L1、L2为两侧漏 感；R1、R2为两侧电 阻；I1、I2和V1、V2分别为两侧电流和电压。可见,上述模型刻画了变压器阻抗特性对其端口电压、电流一阶动态过程的影响。

在电磁暂态仿真中,如果采用变化的励磁电感构建详细的变压器模型,将导致频繁计算导纳矩阵、增加系统节点数、增加仿真耗时等问题。因此,在仿真中更广泛采用的是补偿电流源并联的模型［19-20］,如图2 所示。

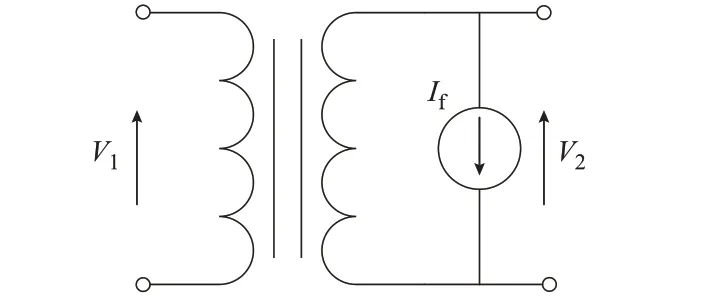
图2 带饱和特性的补偿电流源模型Fig.2 Compensation current source model with saturation characteristics

记变压器空心电抗为LA。为便于分析,可将变压器的磁通量-励磁电流饱和特性曲线（记为λ-I曲线）视为斜率为LA的理想曲线模型,如图3（a）所示。图中：λf为磁芯的磁链；If为励磁电流；λk为磁化曲线简化模型在If=0 时的磁链值；λm为磁链峰值。磁化曲线的简化模型可描述为：

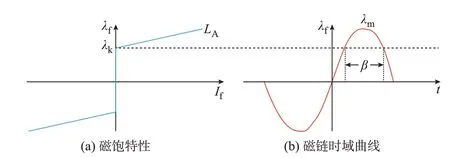
图3 变压器磁饱和特性和磁链时域曲线Fig.3 Magnetic saturation characteristics and magnetic flux time-domain curve of transformer

磁链λf可由式（3）算出,其中,V(t)为变压器端口电压。

在仿真中,变压器磁饱和特性以注入电流的形式并联于绕组端口,其值由式（2）确定。

2.2 磁饱和变压器吸收无功功率水平分析

记V=Vmcos（ωt）,其中,Vm和ω分别为电压幅值和角频率,对应磁链为λf=Vm/［ωsin（ωt）］；磁链峰值λm=Vm/ω。假设产生过电压时,磁链峰值满足λm>λk,则可基于式（2）得到励磁电流随时间变化关系：

其中,β为饱和角,定义为：

从式（4）可以看出,变压器在进入饱和区间后,励磁电流增大,吸收无功功率增多,可以抑制端电压的升高。将式（4）展开为傅里叶级数得：

式中：Ifmn为第n次谐波的分量幅值。

励磁电流基波分量为：

对应地,可以由电压及励磁电流关系式计算得到变压器单相的无功吸收量Qp：

一般地,变压器磁饱和特性曲线可以用拐点电压K（通常取1.15～1.25）和空心电抗LA来表征。拐点电压K由磁饱和特性曲线拟合得到,由铁芯性质决定,可以由图3 中的参数λk及额定电压VN来表示：

进一步,由式（5）、式（8）、式（9）即可计算出过电压发生时进入励磁饱和的变压器单相吸收的无功功率Qp,如式（10）所示。

式中：Vm*为过电压标幺值；SB为变压器基准容量；L*A为空心电抗标幺值,其基值为V2N/（ωSB）。由式（10）可见,在过电压幅值大于磁饱和特性的拐点电压时,变压器吸收的无功功率随过电压幅值增大而增大。

2.3 变压器磁饱和吸收无功功率对过电压的影响

为便于分析,记变压器一次侧为网侧,二次侧为新能源设备。设变压器二次侧的新能源设备发出功率Se=Pe+jQe,等效网侧电势为Ės。记一次侧进线等效暂态阻抗为Zs=Rs+jXs,则系统短路容量Ssc=。进一步,可得等效网侧暂态电势幅值表达式：

式中：U2为变压器二次侧新能源接入点电压幅值；kT为变压器变比；Ėn为网侧暂态电势与二次侧电势同方向的纵向分量；Ėτ为与其正交的横向分量。

由于电压横向分量对电压幅值影响较小,故可忽略电压变化的横向分量幅值｜,只计算电压纵向分量幅值｜的变化,得到变压器端口电压变化量幅值ΔU如式（12）所示。

其中,φsc=arctan(Xs/Rs)。可得二次侧电压为：

式中：Es为Ės幅值。

式（14）表述了过电压随变压器饱和吸收无功功率的变化。结合（10）式中变压器单相吸收的无功功率Qp的计算方法,由（14）式可得到变压器饱和特性对过电压的影响。

3 不考虑变压器磁饱和特性的仿真结果修正方法

工程实践中,常采用未考虑变压器磁饱和特性的机电暂态仿真工具分析系统工频暂态过电压水平。由前述分析可以看出,此类仿真结果可能存在过电压水平偏高的现象,需要适当修正处理,以提升相关分析评估的准确性和针对性。

3.1 机电暂态仿真的变压器模型

电力系统分析中忽略变压器励磁支路,仅考虑短路阻抗,并计及变比影响。记变压器变比为a,短路阻抗为RT+jXT,则机电暂态的变压器模型可以写为：

式 中：İ1、İ2和U̇1、U̇2分 别 为 两 侧 电 流 和 电 压 相 量；YT表达式如式（16）所示。

可见,机电暂态仿真中的变压器仅采用准稳态模型,为代数方程模型,无法准确仿真变压器阻抗及磁饱和特性对电压、电流动态特性的影响,更无法直接获取考虑饱和特性的仿真结果。

3.2 变压器饱和特性对过电压的影响大小分析

式（10）和式（14）分别描述了在过电压为V*m的情形下,变压器因磁饱和吸收的无功功率大小,以及该部分无功功率对过电压的影响。假设在不考虑变压器的饱和特性时,过电压标幺值为V*m0,其对应的Qp=0。修改式（14）,消去Es,可得V*m0和V*m的转换方法：

式中：Qp根据式（10）算出,由考虑磁饱和后的过电压V*m决 定。将 式（10）代 入 式（17）,整 理 可 得式（18）。

其中

隐函数式（18）无法直接得到显式解,只能通过迭代方法,例如,牛顿法、求近似解等。本文先将其泰勒展开,得到式（20）。

进而根据以上方程求解得：

其中,F′(βk)为F(βk)的导数,如式（22）所示。

可通过式（21）隐式求解饱和角β,并进一步根据式（10）得到修正后的过电压值。

3.3 过电压水平值修正流程

对于已有的未考虑变压器饱和特性时得到的过电压仿真结果,应对每个过电压值进行修正。具体的修正流程阐述如下。

1）判断过电压V*m0是否超过相连变压器的饱和拐点K。若没有超过,则处理下一个过电压结果。

2）令饱和角βk=0,初始时k=0。

3）根据式（21）、式（22）计算下一步迭代的饱和角βk+1。

4）重复第3 步,直到迭代收敛。

5）根据式（23）计算修正后的过电压值。

该方法通过对变压器饱和产生的无功补偿特性进行估计,从而完成对过电压的修正。原理上可以用于对未考虑饱和的仿真算法得到的过电压峰值结果进行修正,包括电磁暂态仿真结果和机电暂态仿真结果,修正后的过电压峰值考虑了变压器饱和特性,更为准确可信。

4 算例验证

4.1 小规模算例仿真验证

针对图1 所示单链系统算例,验证前述变压器饱和特性对过电压的影响。表1为算例中220 kV 变压器T1（230 kV/121 kV/37 kV）、110 kV 变压器T2（121 kV/37 kV）、35 kV 变压器T3（37 kV/0.69 kV）的参数、过电压值,以及利用式（21）及式（10）理论计算变压器所吸收的无功功率大小。这里,变压器饱和参数取典型值K=1.17,LA=0.2 p.u.。

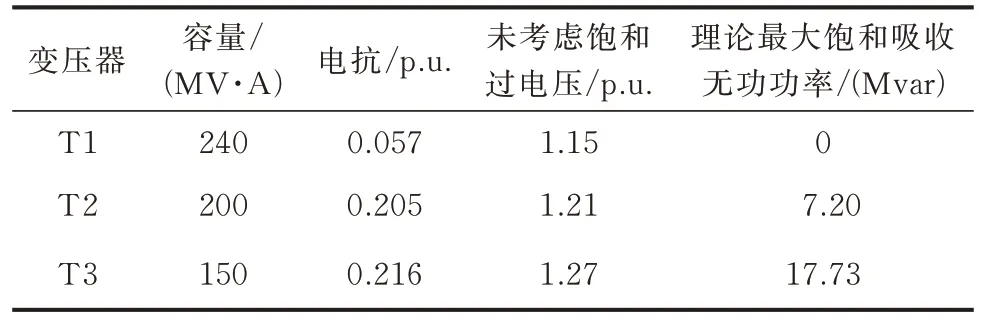
表1 单链路变压器参数及理论饱和吸收无功功率计算结果Table 1 Single-link transformer parameters and theoretical saturation absorption reactive power calculation results

仍以前述直流受端故障场景,比较仿真得到各变压器磁饱和特性吸收的无功功率,以及通过式（10）理论计算得到的无功功率如附录A 图A5 所示。

从仿真结果可见,考虑饱和特性后,110 kV 变压器多吸收了约7 Mvar 的无功功率,35 kV 的变压器吸收了约18 Mvar 的无功功率。数值仿真所得结果大致与表1 所示的理论计算结果相同。说明过电压发生时变压器的磁饱和特性会导致其吸收无功功率,且无功功率吸收量可用式（10）估计。

4.2 西北直流送端电网过电压分析

针对110 kV 及以上电压等级网架,搭建了西北电网全电磁暂态仿真模型,包含10 105 条三相交流母线、206 个风电机组（包括87 个直驱风电机组和119 个双馈风电机组）、249 个光伏电站、641 台同步发电机、1 023 台感应电动机。其中,吉泉直流输电系统严格按照实际工程参数建模,控制器采用直流工程实际控制保护装置。考虑较高新能源出力水平,设计系统运行方式。

为了分析系统故障后过电压水平,在吉泉直流系统受端的古泉500 kV 母线设置短时三相短路故障,故障发生在2.5 s,其后0.02 s 故障切除。故障过程中吉泉直流2/4 号晶闸管出现了直流换相失败现象,故障切除前后系统均保持功角稳定。在此基础上,进一步分析故障引发的暂态过电压问题及其后续影响。

直流近区故障和换相失败引发了各电压等级母线电压显著波动。图4 展示了110～800 kV 各电压等级母线中过电压最严重的母线。

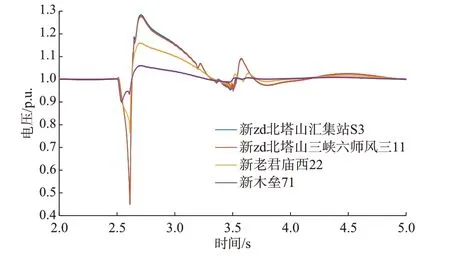
图4 110～750 kV 的各母线电压Fig.4 Voltage of each bus from 110 to 750 kV

选取部分过电压较严重的风电场站,分析变压器饱和特性对这些场站的影响。风机的信息及接入点变压器信息如表2 所示。变压器磁饱和特性参数均取典型值K=1.17,LA=0.2 p.u.。

表2 风电场及接入点变压器信息Table 2 Information of wind farms and transformers at access points

分别考虑/不考虑变压器饱和特性进行系统的电磁暂态仿真,得到这部分风电场站的过电压结果。同时,对不考虑变压器饱和特性的过电压仿真结果,采用本文的过电压修正方法加以修正,共得到3 种结果如表3 所示。

表3 考虑变压器饱和及修正的过电压结果Table 3 Overvoltage results considering transformer saturation and corrected results

考虑变压器饱和及不考虑饱和时风机端电压仿真曲线如图5 所示。

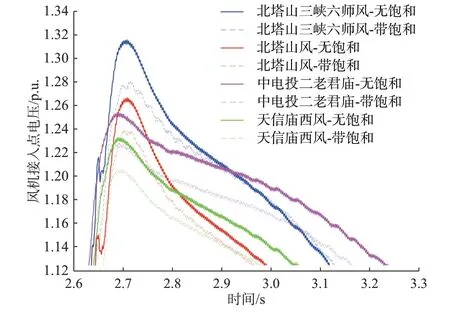
图5 西北电网算例考虑饱和特性的电压曲线Fig.5 Voltage curves considering saturation characteristics of Northwest China power grid case

变压器饱和时吸收的无功功率曲线如图6所示。

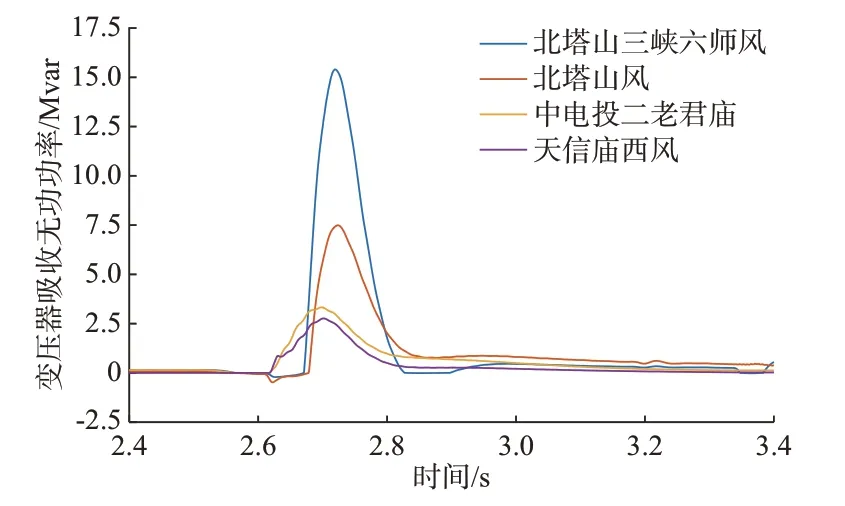
图6 各风电场接入点变压器饱和吸收无功功率Fig.6 Reactive power absorbed by saturated transformers at each wind farm access point

结果显示,通过本文所提修正算法修正后的过电压结果与采用含饱和特性的变压器模型进行电磁暂态仿真得到的结果相近,误差在1%以内,说明了本文提出理论的正确性和过电压幅值修正算法的有效性。

值得注意的是,虽然该修正算法可以应用于修正通过机电暂态仿真得到的过电压幅值,但当需要准确的过电压结果时,仍应采用考虑变压器饱和特性的电磁暂态仿真工具。

5 结语

本文基于全电磁暂态仿真工具,研究变压器饱和特性对新能源接入点过电压仿真结果的影响。仿真结果和理论推导均证明,变压器磁饱和特性对电网过电压分析结论有较大影响,并进一步影响到无功设备规划部署、新能源安控策略设计等。因此,有必要在仿真计算过电压时考虑变压器的饱和特性。本文的主要结论如下：

1）在升压变压器端口过电压较高时,变压器磁饱和特性将吸收无功功率,从而抑制过电压的上升。目前,在基于电网仿真工具的过电压分析中,往往忽略了饱和特性的影响,故仿真得到的部分新能源端口过电压数值偏高。

2）本文开展了变压器的磁饱和特性对系统暂态过电压水平影响的理论分析,给出了变压器磁饱和特性吸收无功功率随过电压幅值、磁饱和特性曲线变化的解析计算方法。变压器饱和吸收无功功率与过电压标幺值、变压器饱和特性曲线及容量相关。

3）本文提出了已有的过电压仿真结果的修正方法。从基础变压器磁饱和特性模型出发,通过理论推导给出了修正后过电压计算式,并设计了修正计算的迭代方法。利用西北实际电网的电磁暂态仿真,验证了本文所提算法的有效性,可以用于修正未考虑饱和特性的过电压仿真结果。

本文为理论推导及仿真验证的简便,采用了单边注入补偿电流源表示饱和特性的变压器模型,这种模型在大部分场景下拥有足够的准确性,但当涉及涌流等饱和较严重的场景时,需要采用更精细的仿真分析模型。后续,一方面可以进一步采用更准确的变压器磁饱和模型进行研究,另一方面将研究风机、光伏等新能源场站控制策略对过电压的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。