市域铁路梁式桥跨结构设计参数研究*

朱永兵 王法武 吴定俊

(1.中铁上海设计院集团有限公司, 200070, 上海; 2.同济大学土木工程学院, 200092, 上海)

市域铁路是一种介于地铁、轻轨和城际铁路之间的城区与郊区的轨道交通,设计速度一般为100～160 km/h。为了满足建设需要,国家铁路局制订和颁布了TB 10624—2020《市域(郊)铁路设计规范》。该规范沿用了GB 50157—2013《地铁设计规范》和TB 10623—2014《城际铁路设计规范》的大部分内容。本文根据T/SHJX 002—2018《上海市域铁路设计规范(试行)》编写前立项课题的研究,结合市域铁路桥梁设计的工作经验,对TB 10624—2020中梁式桥跨结构的设计参数进行了研究。

1 梁式桥跨结构竖向变形设计限值

1.1 梁式桥跨结构竖向变形设计限值制定的主要依据

为保证城市轨道交通列车运行的平稳性,减少列车对桥梁的冲击作用,桥梁设计必须保证一定的刚度。桥梁结构变形限值为梁式桥跨结构在列车设计静活载作用下的跨中挠度容许值,主要反映了梁式桥跨结构的静刚度的大小。该变形限值不是动力参数,但其取值对梁式桥跨结构的动力性能有一定的影响。

刚度是结构产生单位变形时所需的力。梁式桥跨结构的刚度限值, 采用了柔度的概念,即考虑梁式桥跨结构在设计列车荷载下所产生的挠度限值,通常将该限值表示为挠度与跨度之比,即挠跨比限值。由于桥梁的刚度和柔度互为倒数,因此各国桥梁都以挠跨比来表示梁式桥跨结构的刚度限值。

确定梁式桥跨结构挠度限值的主要依据是列车过桥时乘客的舒适度[1]。梁式桥跨结构刚度越大,桥梁变形越小,列车过桥运行越平稳,乘客的舒适度越高。此外,乘客的舒适度还和列车的过桥速度、车辆的动力性能、梁式桥跨结构的跨度,以及轨面的平顺性有关。因此,可根据设计时所确定运营列车的车辆、设计速度及线路等级,通过车桥动力仿真计算或实测来分析列车通过不同刚度桥梁时的车体加速度时程响应,获得乘客的舒适度,从而确定相应的桥梁挠度限值。乘客舒适度的评判与所采用的评判标准和所要求的舒适度等级有关。目前,评判乘客舒适度的主要标准或指标有ISO 2631-1:1997《机械振动和冲击—人体承受全身振动评价—第1部分:一般要求》、Spering(见GB 5599—1985《铁道车辆动力学性能评定和试验鉴定规范》)、Janeway[2]等,评判等级分为优秀、良好、合格及不合格,也有其他评判标准将其分为合格与不合格两个等级,采用不同评判标准和不同等级要求所得到的梁式桥跨结构挠度限值是不同的。

1.2 梁式桥跨结构挠跨比设计限值对比分析

表1为各规范中梁式桥跨结构的挠跨比设计限值。表2为各规范中梁式桥跨结构的当量挠跨比设计限值。由于不同规范中列车荷载设计值差异较大,直接对比各本规范中梁式桥跨结构的挠跨比设计限值不能得到该结构刚度的差异,但将其转换成当量挠跨比就可以得到梁式桥跨结构的刚度。所谓的当量挠跨比,指的是根据各本规范中列车设计荷载获得满足其相应挠跨比设计限值的桥梁刚度。利用GB 50157—2013中的设计荷载重新计算对应桥梁刚度下的挠跨比,即可得到当量挠跨比。

表1 各规范中梁式桥跨结构的挠跨比设计限值

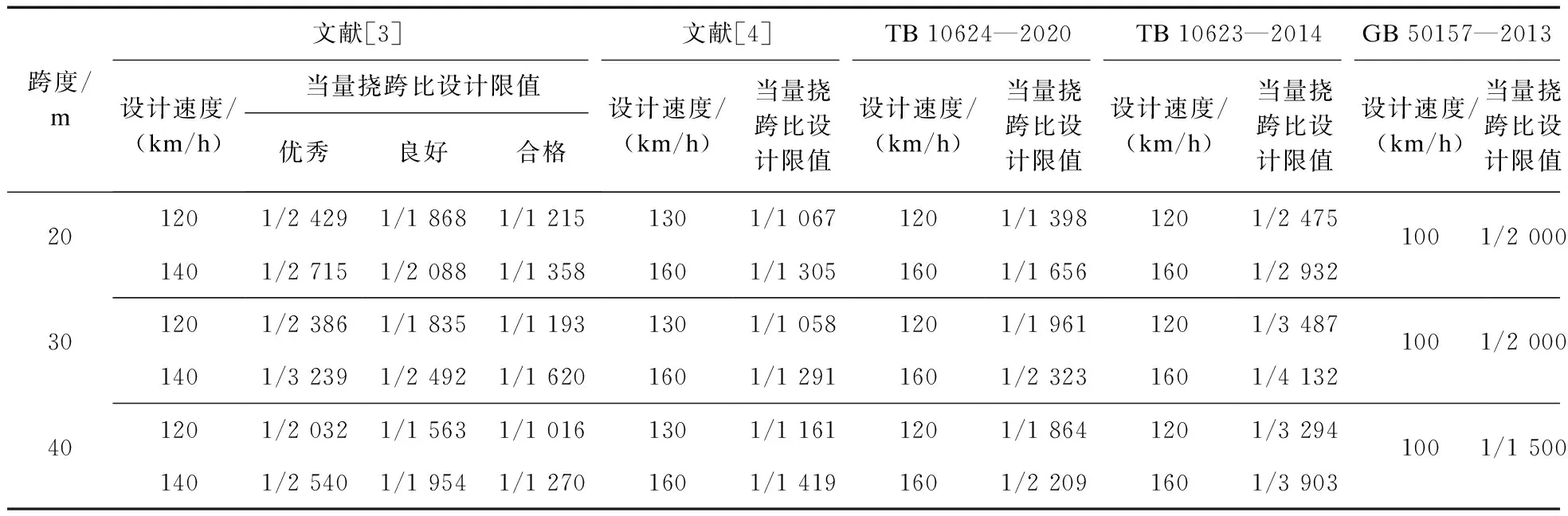
表2 各规范中梁式桥跨结构的当量挠跨比设计限值

桥梁结构的当量挠跨比直接反映了各规范中桥梁刚度设计值的大小。由于挠跨比设计限值与设计速度相关,在设计速度差异较大情况下的桥梁结构当量挠跨比不具有可比性。表1仅列出了设计速度为100～200 km/h范围内的梁式桥跨结构挠跨比设计限值。

从表1中可以看出:

1) 文献[4]中桥梁结构当量挠跨比设计限值与文献[3]中对应的乘客舒适度为合格条件下的桥梁结构当量挠跨比设计限值较为接近,即日本城市轨道交通桥梁刚度设计值要求相对较低。文献[4]制定挠跨比的依据是满足Janeway舒适度等级J=1.5的要求,其对应的最大车体加速度为2.0 m/s2,这与文献[3]中乘客舒适度等级为合格对应的最大车体加速度是一致的。

2) TB 10623—2014中桥梁结构的当量挠跨比设计限值比文献[3]中的乘客舒适度为优秀条件下的桥梁结构当量挠跨比设计限值要求要严格,这表明该规范中桥梁刚度设计值较大,此处考虑了城际铁路设计速度较高的情况。而GB 50157—2013中桥梁结构当量挠跨比设计限值接近文献[3]中舒适度为良好条件下的当量挠跨比,但比文献[4]中的桥梁结构当量挠跨比的限值要严格。由于城市轨道交通设计速度相对较低,因此从乘客舒适度控制角度来看,城市轨道交通桥梁结构刚度设计值相对较大。

3) 我国市域铁路桥梁结构当量挠跨比和城际铁路当量挠跨比相比,在车速相差不大的情况下,挠跨比限值的比值相差接近1倍,即市域铁路桥梁的刚度限值大约是城际铁路的1/2。此差别非常明显,以下对该问题作更加详细的分析。

1.3 TB 10624—2020中挠度设计限值存在的问题

TB 10624—2020中桥梁结构的挠度设计限值完全沿用TB 10623—2014中的相应条文,但未考虑市域铁路和城际铁路之间的差异。城际铁路的车辆选型与高速铁路相近,而市域铁路的车辆选型与城市轨道交通相近。不同类型车辆的动力性能、轴重及荷载分布不同,因此乘客的舒适度对桥梁刚度的要求亦存在差别,且较大的差别是城际铁路列车活载设计值要比市域铁路大很多。

图1和图2为市域铁路和城际铁路列车设计活载图式[5]。由图1和图2可以看出:市域铁路的列车荷载设计值与实际运营的列车非常接近,其中,集中荷载的大小及其分布代表相邻2节车辆间2个相邻转向架的4个轴重的大小和分布,均布荷载为车辆的均布荷载;城际铁路的荷载为概化荷载,其加载图式与文献[4]相同,其大小为文献[4]中荷载的0.6倍,这与实际运营列车荷载在大小及分布方面都有较大差异。

尺寸单位:m

尺寸单位:m

计算表明:跨度为20～40 m范围内时,在相同刚度下,城际铁路列车静活载作用下的简支梁跨中最大挠度效应约为市域铁路的2倍,即市域铁路桥梁结构的抗弯刚度仅需为城际铁路梁桥结构的1/2就能满足条文中的挠度设计限值要求。因此,市域铁路和城际铁路桥梁结构采用相同的挠度设计限值,则市域铁路桥梁结构刚度设计限值相对城际铁路较低,其值约为城际铁路桥梁结构刚度设计限值的1/2。由于桥梁结构刚度减少较为显著,其竖向自振频率相应也将有较大减小。而桥梁结构竖向自振频率是影响车桥耦合振动的重要参数,对车辆过桥舒适度和桥梁振动剧烈程度都有较大影响。因此,市域铁路桥梁结构刚度设计值不宜沿用TB 10623—2014的相应规定,应根据市域铁路的实际车桥条件,分析列车过桥动力响应和乘客舒适度,制定反映市域铁路桥梁自身特点的合理刚度限值。

2 梁式桥跨结构自振频率设计限值

2.1 梁式桥跨结构自振频率设计限值制定的目的

铁路桥梁比公路桥梁更容易产生共振,这是因为铁路桥梁运营的是编组列车。这是一种轴重排列具有规律性的系列荷载,因此容易在一段持续时间内形成具有相对稳定频率作用的激振荷载。当该激振荷载和桥梁自振频率接近时,会引起列车和桥梁共振。而公路桥梁上运营车辆的多样性以及轴重排列的随机性,不太容易形成稳定的加载频率,因此也就不大容易发生共振。早期铁路桥梁设计规范对梁式桥跨结构设计无频率限值要求,但由于运营车速较低,桥梁结构在满足刚度和强度的条件下,列车激振频率一般均远小于其自振频率而不会产生共振现象。城际铁路、高速铁路由于运营车速大幅提高,列车激振频率也随之增大,因此TB 10621—2014《高速铁路》、TB 10623—2014中均考虑了梁式桥跨结构自振基频最小限值的要求,以保证列车激振频率和桥梁的基频保持一定的差值,避免列车通过时桥梁发生较大振动。

目前GB 50157—2013和TB 10624—2020中均未考虑梁式桥跨结构自振频率设计限值的要求。有一种观点认为,地铁、市域铁路设计速度较低,只要保证刚度要求,不必进行自振频率最小限值检算,但这对市域铁路是不合适的。市域铁路的设计速度为160 km/h,某些市域铁路的设计速度达到200 km/h。市域铁路是一种设计速度远高于城市轨道交通且接近城际铁路的轨道交通。市域铁路中列车对桥梁产生的激振频率更接近一般桥梁的自振频率,有可能导致桥梁产生的振动加剧。桥梁结构刚度检算不能代替自振频率检算。刚度是静力学中的参数,是抗静力变形的能力。虽然刚度和结构的自振特性的频率具有相关性,但目前针对桥梁结构刚度和自振频率关系的影响规律研究还不够,制定桥梁结构刚度限值时也未考虑其对动力的影响作用,因此刚度限值检算不能取代自振频率限值检算。特别是TB 10624—2020中关于桥梁结构刚度限值的条文还不是很成熟的情况下,应当添加梁式桥跨结构自振频率设计限值的条文,以确保市域铁路桥梁运营时的良好动力性能。

2.2 梁式桥跨结构自振频率的确定方法

关于市域铁路梁式桥跨结构自振频率的限值,中铁上海设计院集团有限公司在编制T/SHJX 002—2018《上海市域铁路设计规范(试行)》时,与同济大学土木工程学院桥梁系合作对常用跨度简支梁的自振频率限值进行了理论分析。首先确定各常见跨度简支梁的最大容许动力系数Φmax,根据Φmax确定相应梁式桥跨结构的最小自振频率。Φ的计算公式为:

E设计(1+μ)>E运营Φ

(1)

式中:

E设计、E运营——表示设计荷载、实际运营荷载的静载效应,一般常采用跨中挠度;

1+μ——动力系数设计值,根据TB 10624—2020条文说明给定的动力系数计算公式取值;

Φ——不同跨度、不同截面梁式桥跨结构在实际运营荷载下的动力系数容许值。

E设计、1+μ及E运营对于已确定的跨度、刚度、设计荷载,以及T/SHJX 002—2018而言,其值都是已知的,而Φ可从式(1)中求出。对于同一跨度桥梁,Φ值随桥梁的刚度、设计速度等参数的变化而变化。Φmax为该跨度下梁式桥跨结构的动力系数最大容许值。在保证Φ<Φmax的前提下,根据车桥动力仿真分析可以得到不同跨度下梁式桥跨结构的基频下限值。

2.3 梁式桥跨结构自振频率的最小限值

根据上述分析思路,采用市域铁路D型车进行计算,得到市域铁路荷载作用下,简支梁桥跨结构自振频率下限值与跨度的关系[6]:

f0,C=112.23L-1.031

(2)

式中:

L——桥梁的计算跨长,单位m,16 m≤L≤48 m;

f0,C——梁式桥跨结构竖向基频限值,单位Hz。

式(2)中的f0,C与文献[4]中的梁式桥跨结构自振频率下限值f0,JP=55L-0.8比较接近;f0,C与EN 1990中的f0,EN相比,当跨度小于30 m时,f0,C比f0,EN大;当跨度在30～40 m范围内时,f0与f0,EN相当;当跨度大于40 m时,f0,C比f0,EN小。究其原因为我国市域铁路D型车的车速、轴重、轴距,以及车长和定距与日本轨道交通车辆均较为接近。

图3为各规范下市域铁路梁式桥跨结构自振频率下限值对比曲线。

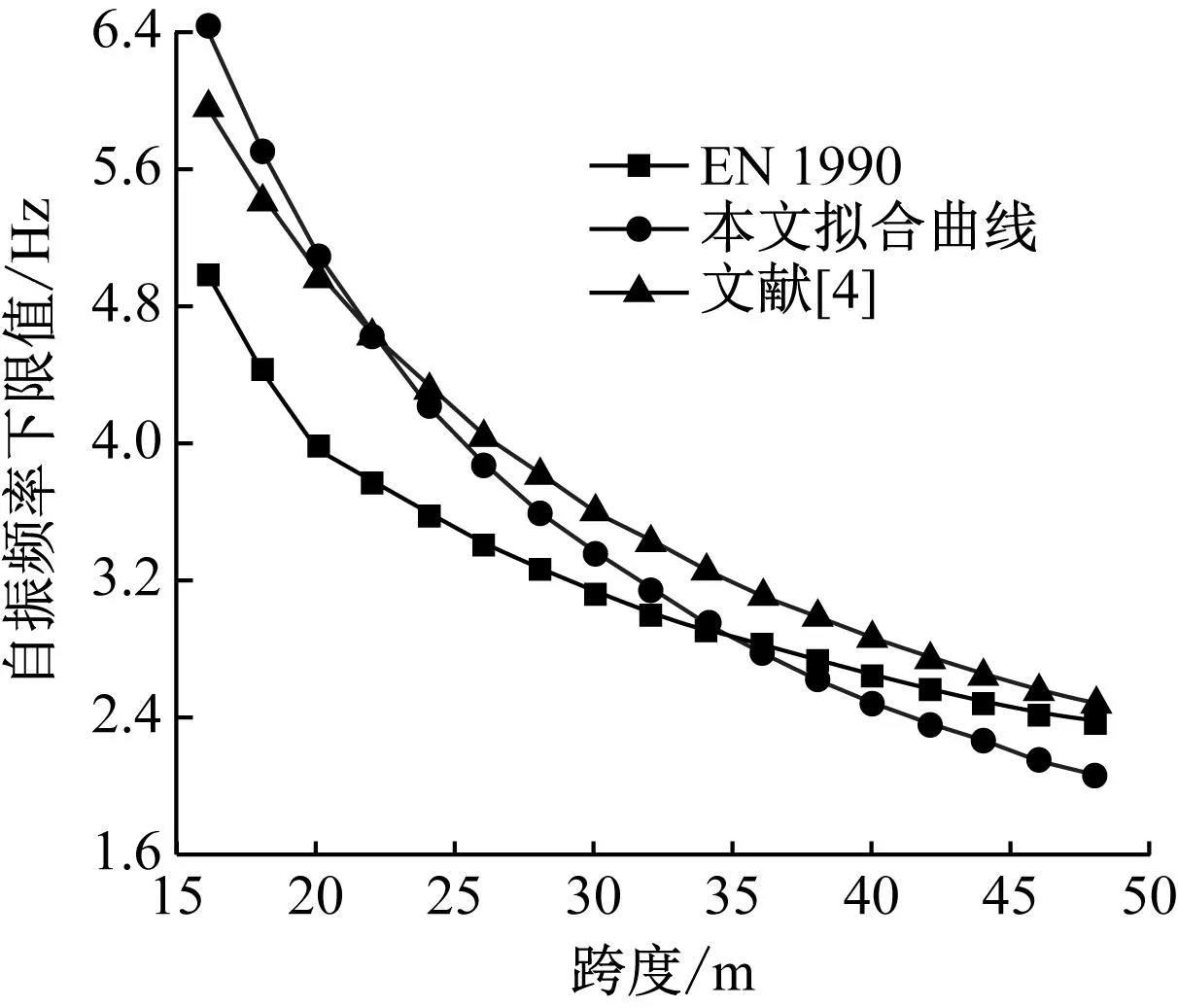
图3 各规范下市域铁路梁式桥跨结构自振频率下限值对比曲线

3 梁式桥跨结构的动力系数

目前TB 10624—2020中桥梁动力系数采用的是客货混跑铁路桥梁的动力系数计算表达式,其中钢筋混凝土桥跨结构的动力系数为:

(3)

式中:

α——系数。

式(3)在我国客货混跑铁路上已经沿用了几十年,它是根据早期蒸汽机车通过常用跨度简支梁桥实测的动力系数经过统计分析而得出的经验公式。如今内燃机车和电力机车已经完全取代了蒸汽机车,设计速度提高了,轴重和轴距也改变了,但该公式仍在沿用。式(3)将动力系数表示为跨度的函数,未反映设计速度、梁式桥跨结构自振频率和刚度,以及轨面平顺度对车桥动力作用的影响,但应用方便简单,基本上能包络住当前客货混跑列车过桥的动力放大作用影响的区域。

动力系数制定的主要目的是考虑桥梁强度检算时列车荷载的动力放大作用。通常将规定的列车静活载效应设计值乘以动力系数来考虑其动力放大作用。我国客货混跑、城际铁路及高速铁路的列车荷载设计值均为概化荷载,其值均比实际运营列车大得多。根据式(1),Φ可以相当大,比直接采用现场实测数据或车桥动力仿真计算数据要大得多。因此,将现场实测和车桥动力仿真计算数据作为制定规范中的动力系数的依据也不是很合理,究其原因为设计荷载和实际运营荷载有较大差别。城市轨道交通和市域铁路的列车设计荷载与实际运营列车的荷载较为接近,因此,其现场实测资料和车桥动力仿真计算数据可作为制定其动力系数的重要依据。

活载作用下简支梁动力系数-跨度关系曲线,见图4。由图4可见:当列车运行速度不超过160 km/h时,不同列车运行速度下梁式桥跨结构的动力系数基本均在式(3)所表示的曲线范围内。这说明TB 10624—2020采用TB 10002.1—2005《铁路桥涵设计基本规范》中客货混运动力系数的计算公式是安全的,也是合理的。

图4 活载作用下简支梁动力系数-跨度关系曲线

4 结语

市域铁路是近年来城市发展中的一种新的轨道交通模式,目前我国不少城市都在开展或规划市域铁路的建设。设计规范是行业技术水平和经验积累的结晶,对工程建设具有重要的指导作用。但设计规范的编制从来不是一蹴而就的,需要在使用过程中发现问题、解决问题及逐步完善。本文的研究成果可为市域铁路梁式桥跨结构设计参数的研究提供参考。