高速及超高速磁悬浮线路平面设计参数研究

黄成名 鲍慧明 张继鹏 王英杰

（1.中铁工程设计咨询集团有限公司，北京 100055；2.北京交通大学，北京 100044）

随着交通强国战略的实施，超高速磁悬浮交通系统作为跨时代的交通工具，在国内受到广泛关注。磁悬浮列车是利用电磁铁产生的磁力悬浮、牵引和导向的新型交通工具，运行速度可达1 000 km／h。相比于传统轮轨交通系统和航空系统，磁悬浮列车具有速度较快、环保节能、平稳性好等优点，因此发展磁悬浮交通对我国运输事业的建设具有重要战略意义［1］。

按照列车运行速度的不同，可将磁悬浮线路分为中低速磁悬浮线路、高速磁悬浮线路和超高速磁悬浮线路。中低速磁悬浮线路的列车运行速度不超过160 km／h，其代表是北京地铁S1线和长沙磁浮快线。高速磁悬浮线路的列车运行速度不超过600 km／h，其代表是上海磁浮示范运营线。超高速磁悬浮线路是指运行速度超过600 km／h，最高速度达到1 000 km／h的磁悬浮线路，一般运行在真空管道中，目前大多处于构想和规划阶段，其代表为马斯克提出的Hyperloop［2］，以及我国正处于建设阶段的高速飞车大同试验线。针对中低速磁悬浮线路，米隆［3］等基于舒适度指标，计算了缓和曲线的线型和长度建议取值。易思蓉［4］等基于车线动力学理论，计算了速度为200 km／h的磁悬浮线路的最小竖曲线半径取值。针对高速磁悬浮线路，代一帆［5］等研究了高速磁悬浮线路设计中，平、竖曲线重叠参数对舒适性的影响规律。谢毅［6］等从舒适性的角度出发，计算了速度为600 km／h的高速磁悬浮线路最小曲线半径及缓和曲线长度取值。针对超高速磁悬浮线路，吴昊［7］等计算了真空管磁悬浮线路的平面参数合理取值。规范及技术标准方面，目前已有中低速和高速磁悬浮线路的技术标准，尚无超高速磁悬浮线路技术标准。

本文根据高速和超高速磁悬浮交通系统的特点，比较了两种线路的悬浮制式差异，对比了线路平面主要参数，并采用车辆-线路动力学仿真模型对平面主要参数取值进行了检算，可为超高速磁悬浮线路设计提供参考。

1 高速及超高速磁悬浮制式差异

磁悬浮线路的悬浮制式有常导电磁悬浮、电动磁悬浮、超导磁悬浮和永磁与电磁混合悬浮等［8］。考虑到速度、安全、经济等多方面的要求，高速磁悬浮线路和超高速磁悬浮线路在悬浮制式选择上有若干异同点。

1.1 高速磁悬浮制式

目前，上海磁浮示范运营线是世界上唯一一条商业运行的高速磁悬浮线路，其采用的制式为常导电磁悬浮。现行规范中对于高速磁悬浮线路也只有针对常导电磁悬浮制式的条文。因此，此处只阐述常导电磁悬浮的情形。

高速磁悬浮线路所用的常导电磁悬浮是指车辆在常温下，利用车辆底部的电磁铁和磁性轨道之间的电磁力实现悬浮，悬浮间隙在10 mm左右，必须通电以维持悬浮状态。

TB 10630-2019《磁浮铁路技术标准》［9］中规定，高速磁浮交通轨距不大于2 800 mm，CJJ／T 310-2021《高速磁浮交通设计标准》［10］规定高速磁浮交通轨距为2 800 mm。

1.2 超高速磁悬浮制式

超高速磁悬浮车辆需运行在低气压的真空管中，其采用的悬浮制式为超导磁悬浮。超导磁悬浮是指车辆上安装有超导体，轨道为永磁体，车辆和轨道之间通过磁通钉扎效应产生悬浮和导向力，其悬浮间隙为10～30 mm，无需通电也可维持悬浮状态［11］。

超高速磁悬浮线路的轨距与真空管的直径有关。其中，邓自刚团队建立的磁悬浮高速试验线中真空管道的直径为4.2 m［12］；某试验线的真空管道内径约为4 m［13］；吴昊计算时采用的管道内径为5.6 m，轨距为1 900 mm；大同试验线的管道内径为5.7 m，轨距为 1 950 mm。

综上所述，高速磁悬浮和超高速磁悬浮悬浮制式的主要区别如表1所示。

由表1可知，相比于高速磁悬浮，超高速磁悬浮主要有悬浮间隙较大、轨距较小的特点，在超高速磁悬浮线路设计时应予以考虑。

2 线路平面主要参数对比

2.1 曲线半径参数

高速及超高速磁悬浮线路的平面曲线半径与轨道梁的制造和施工条件有关，均由式（1）计算：

式中：RH——平面曲线半径（m）；

v——车辆运行速度（km／h）；

α——横坡角（°）；

β——纵坡角，上坡为正（°）；

ay——允许侧向加速度（m／s2）；

g——重力加速度（9.81 m／s2）；

RV——竖曲线半径，上凸为正（m）。

由式（1）可知，最小曲线半径与列车速度、允许的侧向加速度、横坡、纵坡及竖曲线半径取值有关。TB 10630-2019《磁浮铁路技术标准》 中规定，最大横坡为12°，最大允许侧向加速度为1.25 m／s2。CJJ／T 310-2021《高速磁浮交通设计标准》也沿用了此值。较大的横坡可以更好地适应地形，从而降低选线难度。高速磁悬浮车辆运行在开放空间中，最大横坡主要与轨道梁部件受力、制造工艺等因素有关；超高速磁悬浮线路具有轨距较小、悬浮间隙较大等特点，同时考虑横坡对最小曲线半径取值的影响，本文取α为8°、12°、16°进行研究。

利用式（1）计算不同速度下横坡α为8°、12°、16°时的最小平面曲线半径，其中β取0，RV取∞，计算结果如表2所示。

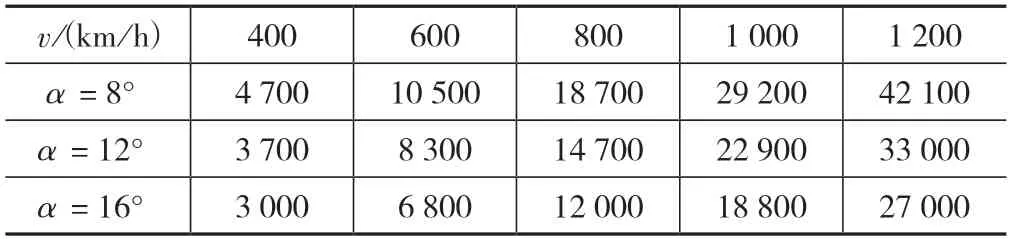
表2 最小平面曲线半径取值表（m）

由表2可知，速度为600 km／h以内时，最小平面曲线半径不超过10 500 m；速度为1 000 km／h时，最小平面半径超过了18 800 m。

2.2 缓和曲线参数

2.2.1 缓和曲线线型

CJJ／T 310-2021《高速磁浮交通设计标准》中规定，直线和圆曲线之间、圆曲线和圆曲线之间缓和曲线线型为正弦型，无夹直线的反向曲线采用一波正弦型缓和曲线连接。根据吴昊研究结果，超高速磁悬浮线路的缓和曲线线型同样推荐采用一波正弦型。

2.2.2 最小缓和曲线长度

CJJ／T 310-2021《高速磁浮交通设计标准》规定缓和曲线最小长度需满足横坡扭转率、侧向加速度时变率和法向加速度时变率的要求。

（1）横坡扭转率

按规范中横坡扭转率限值要求，最小缓和曲线长度按式（2）计算：

式中：LSmin——缓和曲线最小长度（m）；

αa、αe——缓和曲线起、终点扭转角（°）；

Δαmax——最大横坡扭转率（°／m）。

横坡扭转率与车辆运行速度有关，速度越高，允许的最大扭转率越低，且最大扭转率不超过0.05°／m。最大横坡扭转率可按式（3）计算：

由式（3）计算得到的各速度下横坡扭转率如表3所示。

表3 横坡扭转率取值表（°／m）

（2）侧向加速度时变率

参照《高速磁浮交通设计标准》，对于正弦型缓和曲线，取最不利情况，满足最大侧向加速度时变率限值0.5 m／s3要求的缓和曲线最小长度如式（4）所示。

（3）垂向加速度时变率

参照《高速磁浮交通设计标准》，对于正弦型缓和曲线，取最不利情况，满足最大垂向加速度时变率限值0.5 m／s3要求的缓和曲线最小长度如式（5）所示。

式中：bG——车体宽度（按3 m考虑）。

由式（3）～式（5）计算得到的满足横坡扭转率、侧向加速度时变率和垂向加速度时变率要求的最小缓和曲线长度如表4所示。

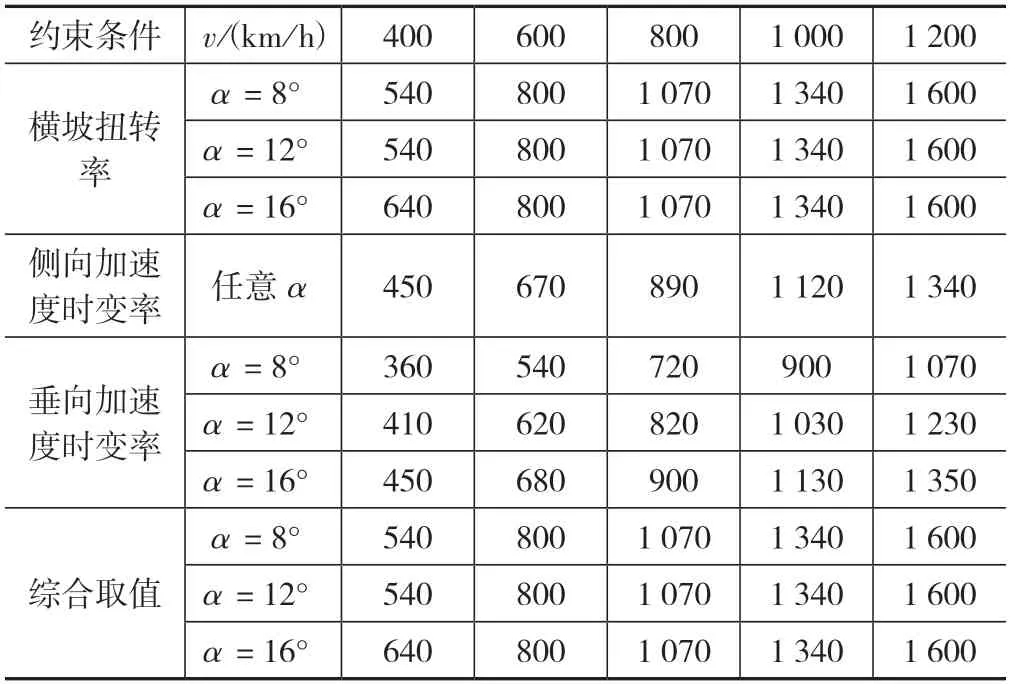
表4 最小缓和曲线长度表（m）

由表4可知，高速磁悬浮线路和超高速磁悬浮线路的最小缓和曲线长度主要由横坡扭转率决定；速度在600 km／h以上时，横坡为8°、12°、16°时的最小缓和曲线长度相同，速度为1 000 km／h时最小缓和曲线长度为1 340 m。

3 动力学仿真对比分析

为了研究高速及超高速磁悬浮线路参数的计算取值的合理性，本文利用多体动力学软件进行了动力学仿真对比分析。利用建立的超高速磁悬浮车辆和高速磁悬浮车辆模型，设置了相应的曲线半径和缓和曲线长度等线路参数，计算了两种车辆在不同参数下的运行状态。对两种车辆运行过程中的车辆振动加速度和电磁力指标进行统计，分析其动力学性能受曲线半径和缓和曲线长度影响的规律，并验证上文计算取值是否合理。

3.1 曲线半径影响分析

模拟一段“缓和曲线+圆曲线+缓和曲线”的线路，选取以下参数进行计算：

（1）超高速磁悬浮：圆曲线转向角为50°，缓和曲线长度为1 340 m，轨距为1.38 m，圆曲线上横坡为16°，车辆运行速度为1 000 km／h。

（2）高速磁悬浮：圆曲线转向角为50°，缓和曲线长度为800 m，轨距为2.8 m，圆曲线上横坡为12°，车辆运行速度为600 km／h。

计算得到的高速磁悬浮各动力学指标与曲线半径的关系如图1所示，超高速磁悬浮各动力学指标与曲线半径的关系如图2所示。

图1 高速磁悬浮动力学指标与曲线半径关系图

图2 超高速磁悬浮动力学指标与曲线半径关系图

由图1可知，车辆振动加速度、悬浮力和导向力均随着曲线半径的增大而减小；曲线半径从 4 000 m增大到8 000 m时，各指标下降较快，8 000 m后继续增大时各指标下降较慢，故上文计算得到的最小曲线半径为8 300 m处于拐点附近，取值较为合理。

由图2可知，车辆振动加速度、悬浮力和导向力大致随着曲线半径的增大而减小；曲线半径从 15 000 m增大到19 000 m时，各指标下降较快，19 000 m 后继续增大时各指标下降较慢，故上文计算得到的最小曲线半径为18 800 m处于拐点附近，取值较为合理。

3.2 缓和曲线长度影响分析

模拟一段“缓和曲线+圆曲线+缓和曲线”的线路，选取以下参数进行计算：

（1）超高速磁悬浮：圆曲线转向角为50°，曲线半径为18 800 m，轨距为1.38 m，圆曲线上横坡为16°，车辆运行速度为1 000 km／h。

（2）高速磁悬浮：圆曲线转向角为50°，曲线半径为8 300 m，轨距为2.8 m，圆曲线上横坡为12°，车辆运行速度为600 km／h。

计算得到的高速磁悬浮各动力学指标与缓和曲线长度的关系如图3所示，超高速磁悬浮各动力学指标与缓和曲线长度的关系如图4所示。

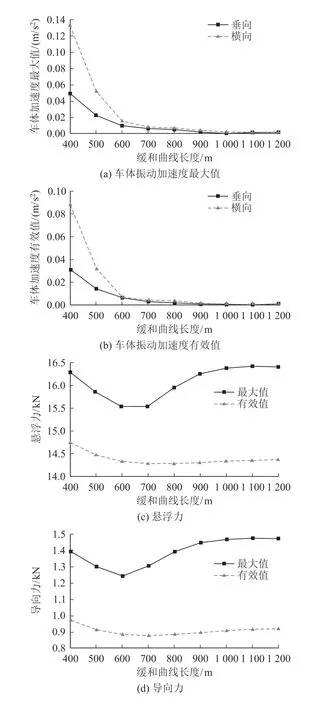
图3 高速磁悬浮动力学指标与缓和曲线长度关系图

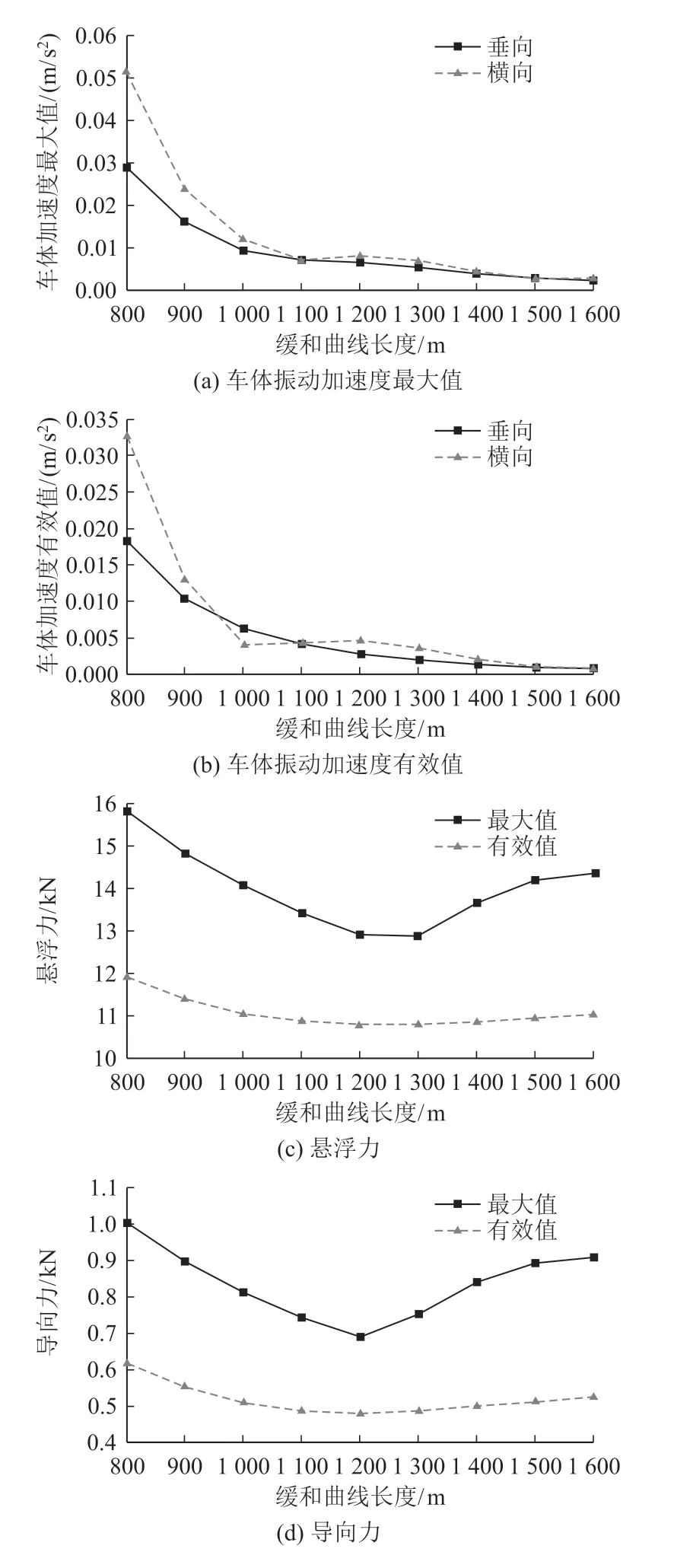
图4 超高速磁悬浮动力学指标与缓和曲线长度关系图

由图3可知，车体垂向加速度和车体横向加速度随着缓和曲线长度的增大而减小，且下降速度逐渐变缓，下降拐点出现在800 m附近；悬浮力和导向力的有效值随着曲线半径的增大而减小，最大值先减小后增大，但拐点都在600 m和800 m之间，而上文计算得到的最小缓和曲线长度800 m处于拐点附近，取值合理。

由图4可知，超高速磁悬浮动力学指标与缓和曲线长度的关系与高速磁悬浮类似，上文计算得到的最小缓和曲线长度1 340 m同样处于拐点附近，取值合理。

综上所述，从动力学评估角度出发，对于超高速磁悬浮线路，最小圆曲线半径取18 800 m、最小缓和曲线长度取1 340 m合理；对于高速磁悬浮线路，最小圆曲线半径取8 300 m、最小缓和曲线长度取800 m合理。

4 结论

本文从磁悬浮轨道交通的基本原理、技术特点等方面出发，对比分析了高速磁悬浮和超高速磁悬浮交通的制式差异和线路平面参数差异，并且采用动力学仿真手段验证了规范公式计算结果的合理性，得到主要结论如下：

（1）在线路设计影响因素方面，相比于高速磁悬浮交通，超高速磁悬浮交通具有悬浮间隙较大、轨距较小的特点。

（2）利用规范理论公式推导得到高速磁悬浮最高设计速度为600 km／h时，对应的圆曲线半径最小值为8 300 m，缓和曲线最小长度为800 m；超高速磁悬浮设计速度为1 000 km／h时，对应的圆曲线最小半径为18 800 m，缓和曲线最小长度为1 340 m。

（3）车辆-线路动力学仿真结果表明，规范得到平面参数取值比较合理。本文研究成果可为高速及超高速磁悬浮线路平面设计提供理论依据和技术指导。