400 km/h高速铁路小半径曲线地段橡胶浮置板轨道参数优化研究
2024-03-27臧传臻
臧传臻
(中国铁路设计集团有限公司,天津 300308)
橡胶减振垫浮置板轨道是将整体道床与基础分离,做成有足够刚度和质量的道床板,并浮置于橡胶减振垫上,构成了质量弹簧系统,其减振原理是在轨道上部建筑和基础之间插入一个固有频率很低的线性谐振器,防止由钢轨传来的振动传入基础。自1973年 以来,减振垫浮置板轨道在全球100多个国家城市轨道交通项目中得到广泛应用,使用量超过100万m2。该系统在德国柏林地铁铺设使用了30多年,至今减振效果优良。橡胶减振垫浮置板轨道在台湾高雄地铁实测减振效果达到23 dB。轨道不平顺和小半径曲线线路参数作为导致轮轨振动的激扰源,直接影响列车安全平稳运行[1]。然而,目前我国对400 km/h高速铁路橡胶浮置板轨道动力特性的研究还不完善,对高速铁路小半径曲线地段橡胶浮置板轨道的减振效果及参数优化的研究很少。因此,有必要研究轨道不平顺和曲线因素共同作用下的橡胶浮置板轨道结构动力响应峰值。
国内外相关学者已对高速铁路列车动力学响应规律进行了一定研究:杨吉忠[2]等研究了400 km/h行车速度条件下高速铁路轨道几何不平顺的敏感波长;Karis[3-4]等分析了轨道不平顺对车辆动力响应的影响;练松良[5]等针对客货共线铁路,研究了多种类型车辆的车体加速度同轨道不平顺的关系;高建敏[6]等分析了轨道不平顺波长变化所引起的高速铁路列车动力响应变化规律;杨飞[7]等针对CRH2动车组对比分析了速度为300 km/h、350 km/h时轨道不平顺波长对车辆动力响应的影响;徐金辉[8]等分析了轨道参数、车辆悬挂参数、车速对敏感波长的影响;袁玄 成[9]等通过改变各类轨道不平顺的波长及幅值,研究了动力响应变量的变化规律;芦睿泉[10]等对比分析了多种类型轨道不平顺下的动力响应峰值,从而确定了需重点关注的轨道不平顺类型。
为研究400 km/h车速下小半径曲线地段橡胶浮置板轨道动力响应特性,本文建立了7 000 m半径曲线地段CRH380B车辆-轨道动力学模型,分析轨道参数对插入损失的影响规律,确定了400 km/h高速铁路橡胶浮置板轨道参数合理值。研究结论可为运营期高速铁路橡胶浮置板轨道的减振效果评价提供理论依据。
1 动力学模型建立
根据CRH380B车辆参数(如表1所示),从下向上依次设置轮对、构架、车体等刚体,输入各部件的质量、转动惯量及质心坐标等,然后将各部件间通过铰、力元等连接,最终组装成动力学模型。
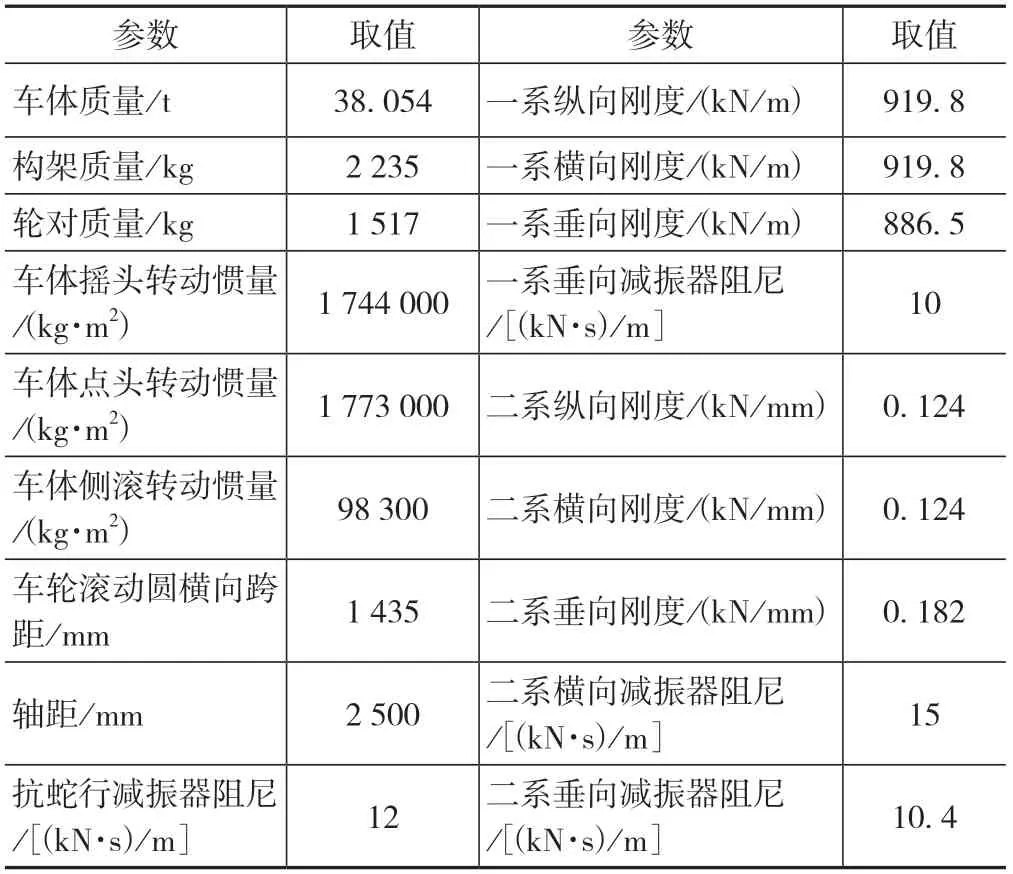
表1 车辆主要参数表
采用S1002G型车轮磨耗踏面、FASTSIM简化轮轨接触算法理论,构建车辆动力学仿真模型。
建立轨道结构有限元模型,钢轨采用Euler梁单元,扣件采用线性弹簧,道床板、自密实混凝土层、橡胶减振垫、底座板和下部基础均为实体单元,有限元模型如图1所示。
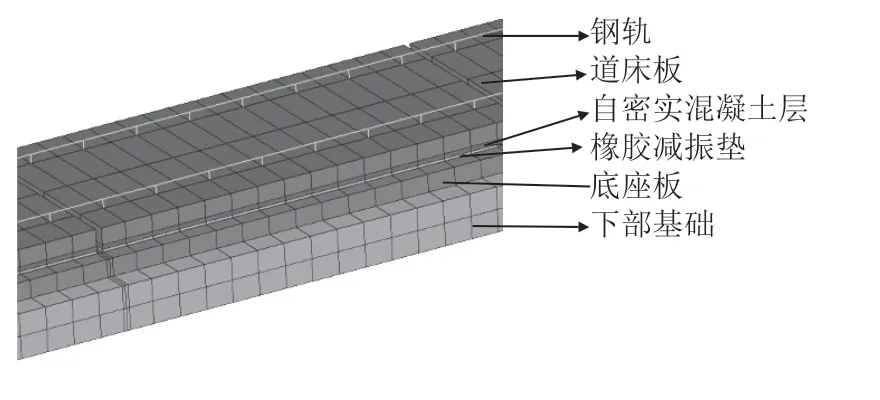
图1 橡胶浮置板轨道模型图
钢轨采用60 kg/m钢轨、材质为U71MnG,采用 1/40的轨底坡,轨距取1 435 mm。扣件节点垂直静刚度为35 kN/mm。道床板材料为C60混凝土,长5.6 m、宽2.5 m,相邻道床板之间缝隙0.07 m。自密实混凝土层材料为C40混凝土,长度和宽度与道床板相同,厚0.1 m。底座板材料为C40混凝土,长度与道床板相同,宽3.1 m、厚0.3 m。自密实混凝土层与底座板之间设置橡胶减振垫,面积与道床板相同,厚度为0.03 m。
根据GB/T 5599-2019 《机车车辆动力学性能评定及试验鉴定规范》[11]的规定,在车厢地板面上布设车体加速度测点,并令转向架中心在地板面的投影点与该测点位置横向相距1 m。采用某高速铁路2 000 m 区段的轨道不平顺,构建相应的无砟轨道结构模型,并基于该区段的列车实测数据进行模型验证。实测轨道不平顺如图2所示。车体垂向、横向加速度时频如图3、图4所示。
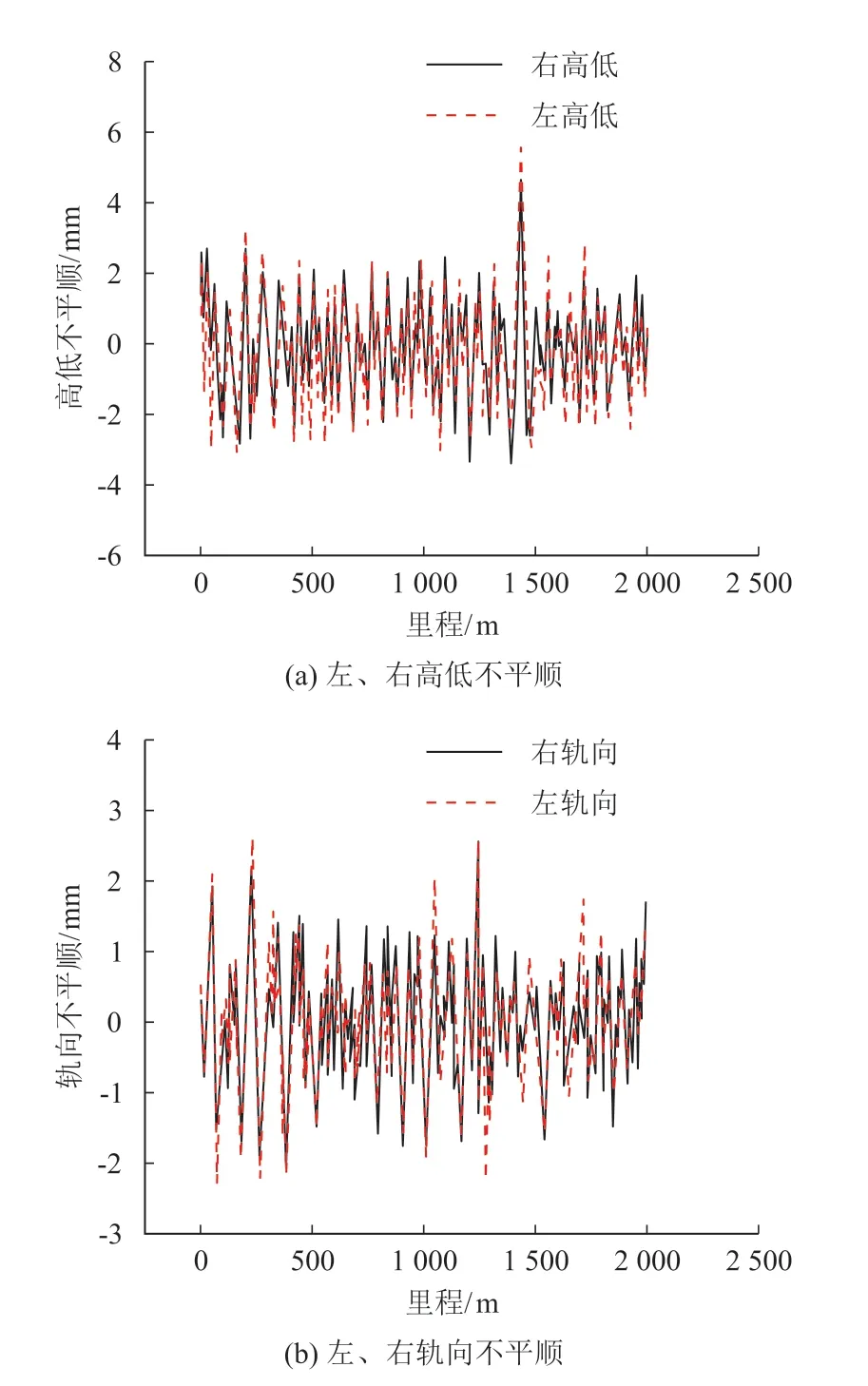
图2 实测轨道不平顺图
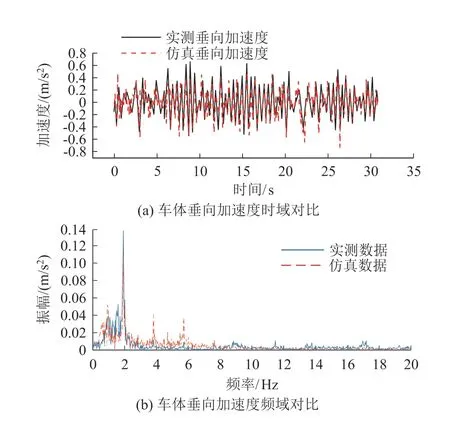
图3 车体垂向加速度时频域对比图
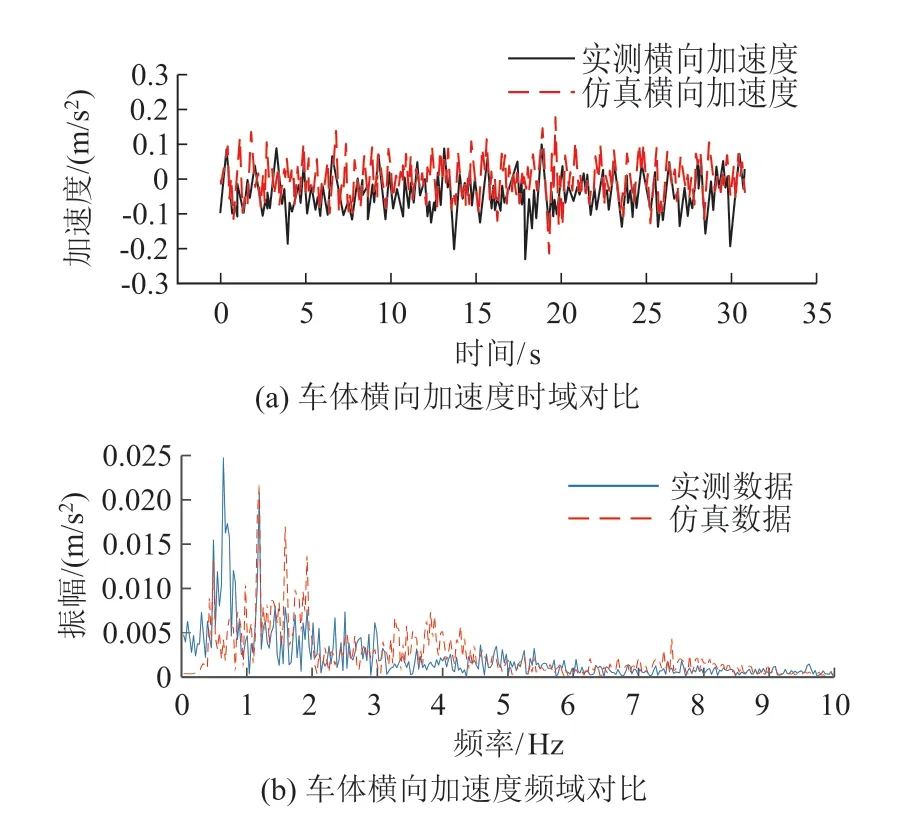
图4 车体横向加速度时频域对比图
由图3、图4可知,车体垂向加速度的仿真与实测数据在时域和频域上均能得到较好的对应。车体横向加速度相对垂向加速度的对应效果较差,主要是因为仿真模型中的车辆参数进行了适当简化,且实际中车体横向加速度的影响因素更为复杂。然而,仿真计算数据与实测数据在时域幅值上接近且线形相似,在频域上各峰值位置与线形走向也相近。
总的来说,仿真与实测数据有较好的相关性,表明仿真模型的计算结果合理。
2 轨道参数优化研究
TB 10621-2014《高速铁路设计规范》[12]中规定,超高、欠超高的最大值分别为175 mm、90 mm,可知400 km/h车速下所允许设置的最小曲线半径近似为7 000 m,因此模型中的曲线半径均设为7 000 m。轨道不平顺采用某高速铁路区段实测数据,模拟列车以400 km/h速度通过直线、缓和曲线和圆曲线(R= 7 000 m,h=175 mm)的工况。
2.1 不同位置处振动响应变量时程曲线
通过分析列车通过橡胶浮置板轨道时,不同位置处的加速度时程曲线如图5所示。由图5可知,道床板中部处钢轨加速度峰值明显大于道床板端部处钢轨加速度峰值,道床板端部处加速度峰值明显大于道床板中部处加速度峰值,道床板端部处底座加速度峰值和道床板中部处底座加速度峰值大致相等,底座处加速度峰值和隧道壁处加速度峰值大致相等。

图5 轨道结构不同位置处垂向加速度时程曲线图
2.2 减振垫刚度对减振效果的影响
选取减振垫刚度为0.019 N/mm3、0.033 N/mm3、0.042 N/mm3、0.1 N/mm3,各部分垂向加速度如图6 所示。底座板垂向加速度1/3倍频程分频振级如 图7所示。
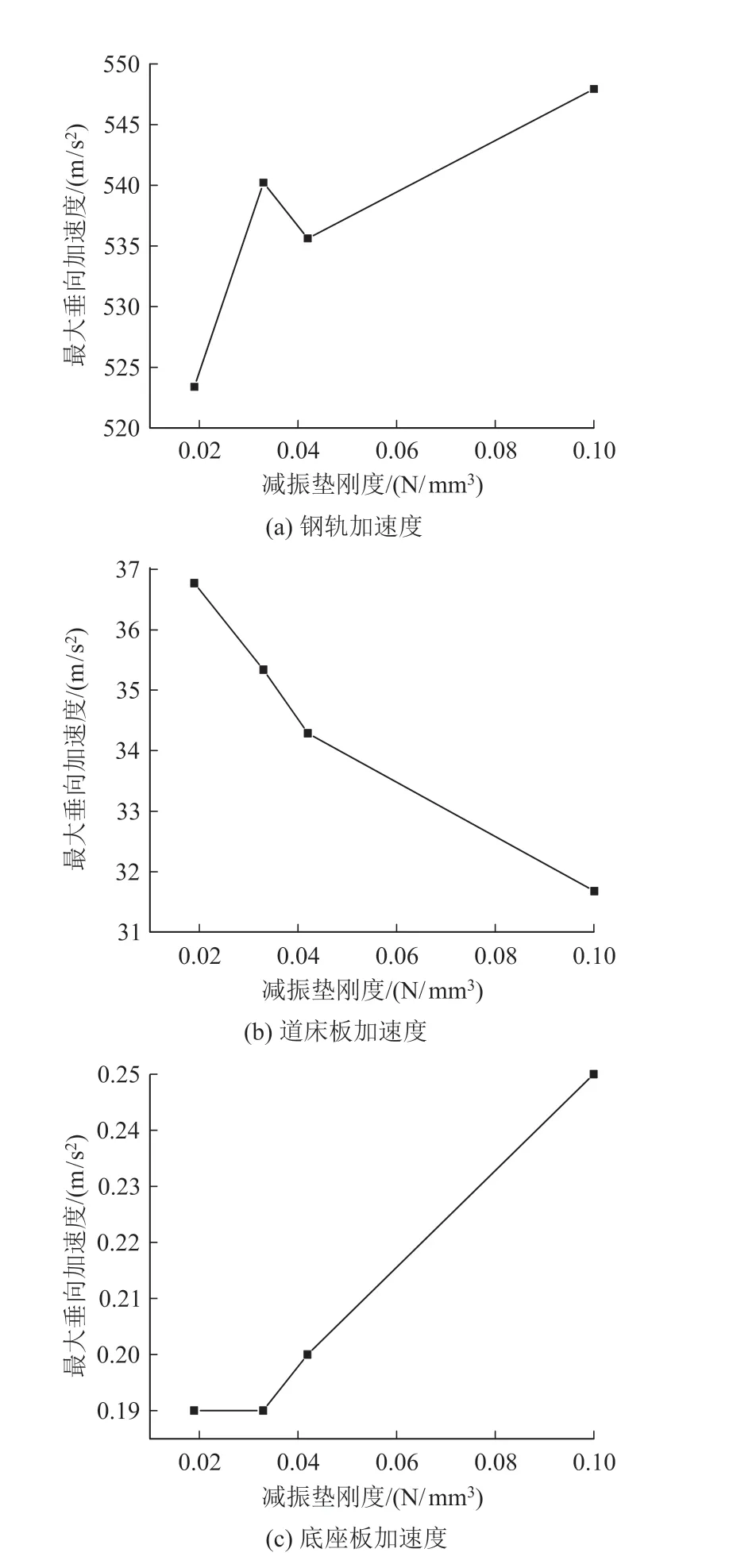
图6 轨道结构各部分最大垂向加速度和减振垫刚度的关系图

图7 底座板垂向加速度分频振级图
由图6、图7可知,当减振垫刚度增大时,钢轨垂向加速度改变不显著,道床板垂向加速度变小,底座板垂向加速度变大;减振垫刚度分别为0.019 N/mm3、0.033 N/mm3、0.042 N/mm3、0.1 N/mm3的情况下,底座板垂向加速度Z振级分别为66.2 dB、66.2 dB、67.1 dB、71.0 dB。当去除轨道结构中的减振垫后,底座板垂向加速度Z振级为79.6 dB,故橡胶浮置板轨道结构的插入损失分别为13.4 dB、13.4 dB、12.5 dB、8.6 dB。
2.3 道床板厚度对减振效果的影响
道床板厚度取0.2 m、0.3 m和0.4 m时,轨道各部分的最大垂向加速度如图8所示。

图8 轨道结构各部分最大垂向加速度和道床板厚度的关系图
道床板厚度对底座板垂向加速度分频振级的影响如图9所示。

图9 道床板厚度对底座板垂向加速度分频振级的影响图
由图8、图9可知,随着道床板厚度增大,道床板、底座板的垂向加速度变小,钢轨垂向加速度变化不大。当道床板厚度为0.2 m、0.3 m和0.4 m时,底座板垂向加速度Z振级分别为73.5 dB、66.2 dB和60.1 dB。考虑轨道结构高度以及限界的影响,道床板厚度宜采用300 mm。
2.4 行车动力响应特性
当道床板越厚或减振垫刚度越大时,轨道动力响应和行车动力响应越小。当道床板厚度采用300 mm时,为了兼顾行车安全舒适性和减振性能,基于动力学仿真可确定合理的减振垫刚度取值为 0.03 N/mm3。减振垫刚度取0.03 N/mm3时列举的行车性能指标时程曲线如图10所示。将各指标的计算结果进行统计可知:车体垂向加速度峰值约为 0.4 m/s2,车体横向加速度峰值约为0.5 m/s2,轮重减载率峰值约为0.4,脱轨系数峰值约为0.75,轮轨垂向力峰值约为105 kN,轮轴横向力峰值约为50 kN,均满足相关控制标准且具有一定安全富余量。

图10 行车性能指标时程曲线图
3 结论
本文研究了400 km/h高速铁路列车行驶至7 000 m 半径曲线地段时的动力响应规律,分析了轨道参数对振动特性的影响,得到主要结论如下:
(1)道床板中部处钢轨加速度峰值明显大于道床板端部处钢轨加速度峰值,道床板端部处加速度峰值明显大于道床板中部处加速度峰值,道床板端部处底座加速度峰值和道床板中部处底座加速度峰值大致相等,底座处加速度峰值和隧道壁处加速度峰值大致相等。
(2)随着道床板厚度的增加,钢轨垂向加速度变化不大,道床板和底座板的垂向加速度减小。道床板厚度的增大,可以提高减振轨道的减振效果。考虑轨道结构高度以及限界的影响,道床板厚度宜采用 300 mm。
(3)减振轨道与普通轨道相比,底座板振动整体减小。减振垫刚度为0.019 N/mm3、0.033 N/mm3、0.042 N/mm3、0.1 N/mm3时,底座板垂向加速度Z振级分别为66.2 dB、66.2 dB、67.1 dB和71.0 dB,普通轨道的底座板垂向加速度Z振级为79.6 dB。减振垫铺设刚度为0.019 N/mm3、0.033 N/mm3、0.042 N/mm3、0.1 N/mm3时,减振效果分别为13.4 dB、13.4 dB、12.5 dB和8.6 dB。考虑行车安全舒适性和轨道结构稳定性,建议减振垫刚度采用0.03 N/mm3。
