螺旋微反应器内传热过程模拟仿真与尺度放大

2024-03-27李玉光赵双飞聂莹莹

含能材料 2024年3期

李玉光，袁飞，赵双飞，，聂莹莹，赵跃，何伟，郭凯

（1.南京先进生物材料与过程装备研究院有限公司，江苏南京 211299； 2.南京工业大学生物与制药工程学院，江苏南京 211816）

0 引言

近年来，由于具有流动可控、传递高效的微尺度效应，微化工技术在含能材料领域得到快速发展［1-5］，被广泛应用于含能材料的合成［6-8］、结晶调控［9-10］和复合含能材料的制备［11-12］等过程中。其中，硝化、氟化、叠氮化等含能材料及其助剂的制备过程需要释放大量热量，热量传递不及时将会存在潜在的危险［13-15］。而微反应器作为微化工过程强化的核心装备，其内部的传质传热效率是实现含能材料安全可控制备的关键［16-17］。

计算流体力学（CFD）数值模拟研究方法能够克服实验研究中的局限性，从物理、计算的角度探究流场内部流动和流动特性，实时监测和准确测量实验参数，避免了实验研究过程中人力物力的浪费［18-19］。Wang 等［20］采用CFD 模拟仿真方法，研究了微通道几何参数和流体的体积分数对努塞尔数（衡量流体换热程度的重要参数）和热阻的影响，结果表明微通道能有效提高传热性能。Kim 等［21］在二维通道的两侧壁面上安装了周期性的肋，以便增强湍流传热，研究了肋条的宽高比、肋条高度和肋条节距比对传热的影响，利用加权因子对结构进行了优化，提升了微反应器的传热性能。Yuan等［22］利用正弦波和直通道对甲醇重整制氢反应进行模拟仿真研究，发现该类型流体通道在提高传热传质和氢气产量方面有较大优势。Gao 等［23］基于CFD 成功模拟了新型微反应器件的热和流体动力学特性，发现其可作为一种初步且经济的方法，指导药物纳米晶体的连续生产，这是医药领域的一项重大进展。综上所述，采用CFD 模拟仿真方法，可以快速获得微反应器中的流场、温度场、压力场等物理量的分布，考察微反应器内流动与传热规律，实现微反应器的设计与开发，为微化工工程化设计提供重要参考。

在实际研究与生产过程中，通常将微通道螺旋盘绕形成螺旋微反应器，以提升传质与换热效率、实现含能材料制备过程强化［24-25］。为此，国内外学者开展了螺旋管内的流动与传热规律的研究。Izadi 等［26］采用人工神经网络和自适应神经模糊推理系统模型评估微螺旋盘管中的微混合性能。Xie 等［27］采用高速显微镜摄像系统，研究了膜分散螺旋微反应器中哌拉西林的合成反应动力学。Veluturla 等［28］考察了螺旋管微反应器内的传热和混合能力，实现生物柴油的连续化高效合成。但目前仍缺乏对螺旋管传热性能的多尺度与尺度放大研究［29-30］。

本研究采用CFD 模拟仿真方法，以螺旋微反应器作为研究对象，在液体层流流动状态下，研究螺旋微反应器的曲率、无纲量螺距对不可压缩牛顿流体流动与传热的影响。同时，对比螺旋微反应器与直通道微反应器的传热性能，并分析螺旋微反应器应用到工业生产的放大效应，以达到高传热性能、低流动阻力、低压降、高通量的目的，为微反应器的设计与优化提供理论依据。

1 模型建立与验证

1.1 模拟计算控制方程与边界条件

为了简化微反应器内耦合传热模型的数值方程，本研究提出了如下假设：1）管内流动流体为不可压缩牛顿流体；2）管内流体的物理性质恒定；3）管内流体和管壁之间无滑移；4）忽略浮力、粘性加热、自然和辐射传热；5）管内流体流动为稳态；6）忽略外部流体与管壁的传热，只研究管壁与内部流体之间的热量传递。

基于以上假设，微反应器内的流体流动、温度分布、压力分布等情况可以由以下连续性方程、动量方程和能量方程控制［20-21］：

式中，u为速度矢量，m·s-1；ρ为流体密度，kg·m-3；p为流体压力，Pa；μ为流体黏度，Pa·s；cp为流体在恒定压力下的比热容，J·kg-1·K-1；T为温度，K；k为流体的导热系数，W·m-1·K-1。

由于液体水与大部分反应溶液具有相似的流动特性，通常被用作微反应器模拟仿真的流体工质［31］。因此，本文选用液态水（ρ=998.2 kg·m-3，μ=1.003×10-3Pa·s，k=0.6 W·m-1·K-1，cp=4182 J·kg-1·K-1）作为研究对象。微反应器的入口为速度入口，入口速度根据雷诺数（Re）进行计算，流体进入微反应器的温度保持恒定，初始温度为293.15 K。微反应器的出口为压力出口，外界压力为0。微反应器的管壁采用恒温壁面边界条件，管壁的温度为373.15 K。

对于螺旋微反应器内的单相流动状态，Srinvasan等［32］采用了如下临界雷诺数计算公式：

式中，Re 为雷诺数，当Re≤Recr时，螺旋管内流体为层流流动；当Re＞Recr时，螺旋管内流体为湍流流动。本研究Re范围为0～200，均小于Recr，处于层流状态，因此计算采用Laminar 层流模型。

由于本研究只关注管壁与内部流体之间的传热效果，因此采用稳态计算。此外，在求解设置中，采用SIMPLEC 压力基求解器，对流体流动变量中的速度、压力、温度等进行耦合迭代计算，在每次迭代中更新雅克比矩阵，收敛准则为迭代过程中各监测物理量残差小于10-4。

1.2 螺旋与直通道微反应器模型建立

微通道内的流体碰撞到壁面后会形成与壁面相反方向的二次流扰动，螺旋微反应器的通道壁面发生连续改变，易形成连续变化方向的二次流扰动［22］。因此，本研究选用螺旋微反应器作为研究对象，考察其内部的传热性能。螺旋微反应器的物理模型如图1a 所示，其整体结构由一个入口、一个出口和螺旋形管壁构成。该物理模型包含螺旋管道半径r、螺旋高度H、螺旋半径R和螺距b四个结构参数。为了验证螺旋微反应器在传热性能上的优越性，选择相同长度的直通道微反应器作为对比研究的对象，如图1b 所示。螺旋微反应器和直通道微反应器的结构模型在Solid-Works［31］中通过圆环分别扫描螺旋线和直线绘制而成。

图1 微反应器物理模型Fig.1 Physical model of spiral and straight microreactor

1.3 模拟计算网格划分

采用ANSYS Workbench 自带的前处理功能对螺旋微反应器内流体模型进行网格划分，在Re=1500 条件下，调整网格数分别为9 万，23 万，52 万，104 万，272 万和567 万，对螺旋微反应器的传热进行网格独立性研究，结果如图2 所示。

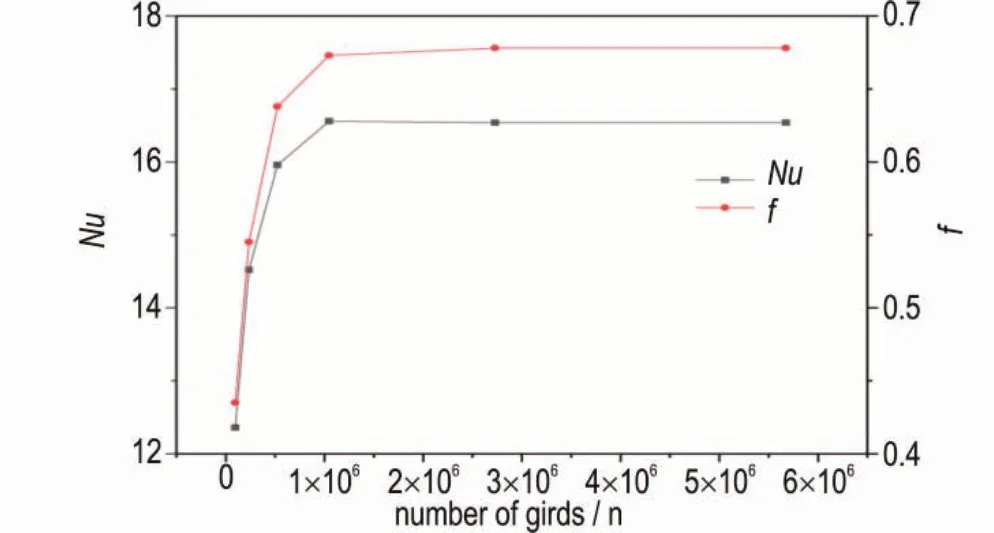
图2 不同网格努塞尔数（Nu）和流动阻力系数（f）的变化Fig.2 Variations of Nu and f under different grids

图2 是网格独立性检验折线图，可以看出当网格数量小于104 万时，努塞尔数Nu和流动阻力系数f随网格数增大而增大；而当网格数大于104 万时，Nu和f基本趋于稳定。因此，通过对模拟计算精度和效率的综合考量，确定104万网格数为最优条件，后续将采用104万网格进行计算模拟，其网格尺寸为0.6 mm，网格划分如图3 所示。

图3 流体模型网格划分Fig.3 Fluid model grid partitioning

1.4 模拟计算验证

以直通道微反应器内层流流动与传热作为研究对象，将本研究建立的模拟仿真模型与文献［33］中经验公式（5）～（6）计算得到的传热性能（Nu和f）进行对比，以验证本研究建立的流动与传热模型的准确性。

其中，直通道微反应器均匀壁温下的平均Nu可采用文献经验Sieder-Tate 公式计算［33］：

流动阻力系数f 的计算公式如下：

式中，Re为雷诺数（Pr为普朗特数

将本研究的模拟仿真计算结果与采用文献经验公式（5）和（6）计算得到的结果进行了对比，结果如图4所示，发现模拟结果与公式的计算结果较吻合，其中努塞尔特数Nu的偏差为0.31%～3.85%，阻力系数f的偏差为1.26%～2.82%，偏差均小于3.85%。由此可见，本研究的数值模拟方法是可靠的。

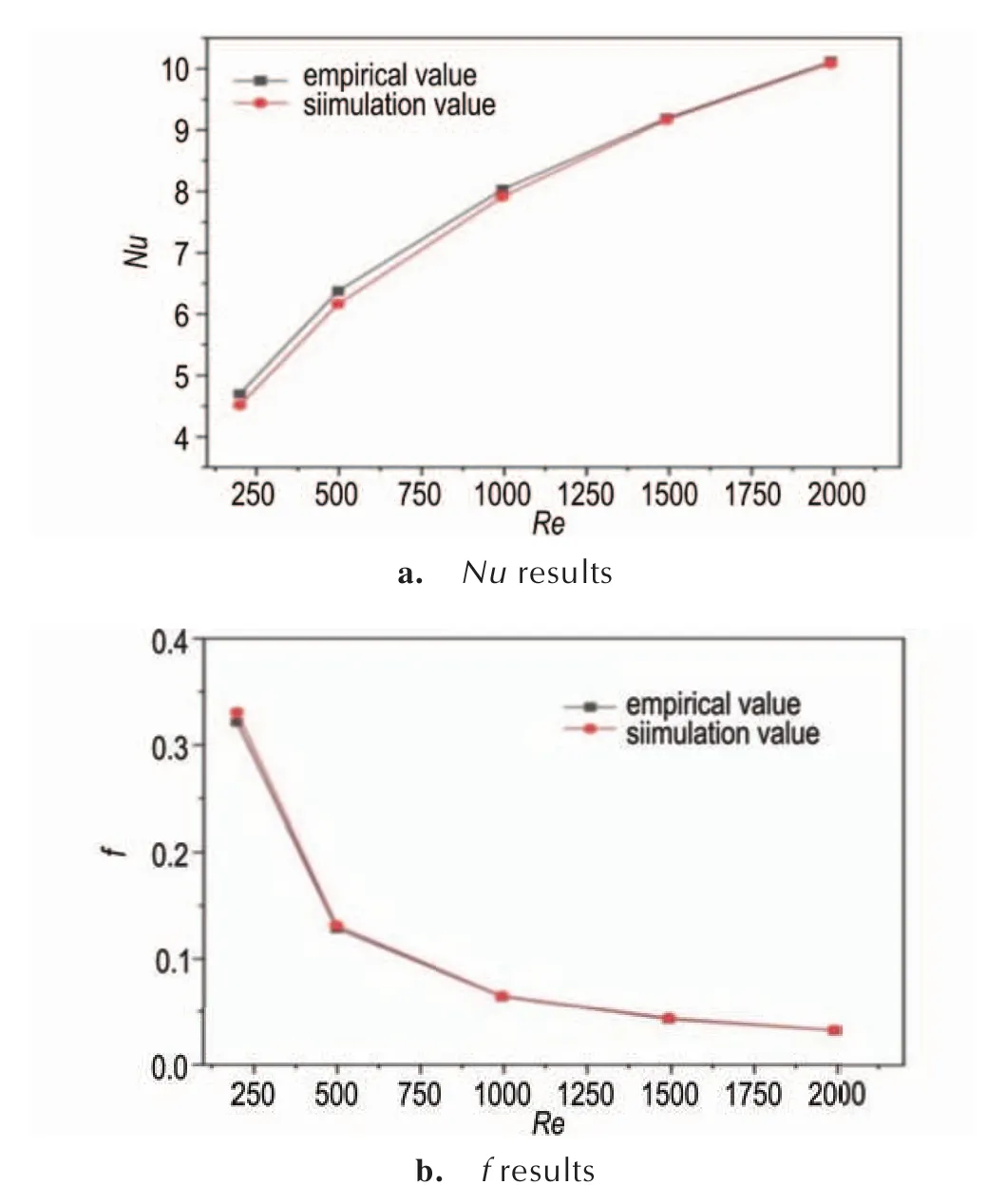
图4 Nu 和f 模拟结果与文献经验公式［33］的比较Fig.4 Comparing the simulation-derived Nu and f results with those obtained from empirical formulas［33］

2 传热过程模拟

2.1 尺寸放大效应的模拟研究

增大管道内径尺寸能够有效提高换热的通量，有利于实现螺旋微反应器换热过程的放大。为了确保螺旋微反应器管道在放大的同时，维持较高的传热性能，通过调整螺旋微反应器通道半径的尺寸，来考察多尺度螺旋微反应器内的传热性能。在螺旋管的总长度H为1000 mm，δ=0.2，λ=0.1，Re=1000 参数设置下，采用模拟仿真方法，考察管道半径r为0.5，1.0，1.5，2.0 mm 和2.5 mm 时的流动与传热规律。

2.2 结构参数对螺旋微反应器传热的模拟研究

为了更有效地分析流体在螺旋微反应器内阻力系数和能量传递，研究不同结构参数对传热的影响，对不同结构参数螺旋微反应器物理模型进行数值模拟研究。定义的螺旋的曲率δ=r/D，无量纲螺距λ=b/2πR。分析在常壁温度边界条件下，螺旋管的曲率δ和无纲量螺距λ对微反应器内流动过程中的传热努塞尔数Nu和沿程阻力系数f产生的影响，确定最优螺旋微反应器结构参数。螺旋管的总长度H为1000 mm，在保持螺旋半径，螺旋通道半径和无量纲螺距条件一致的情况，仅针对雷诺数Re在0～2000 范围进行模拟计算，探索不同曲率δ和雷诺数Re对努塞尔数Nu和阻力系数f作用的影响。此外，在保证其他条件一致的情况下，探索不同无纲量螺距λ和雷诺数Re对努塞尔数Nu和阻力系数f的影响规律。采用Fluent 软件对不同结构参数的螺旋微反应器进行模拟，具体尺寸参数见表1。

2.3 直通道与螺旋微反应器对比

对比直通道与螺旋微反应器的传热性能，考察螺旋微反应器对流体流动与传热的强化作用。直通道和螺旋管的总长度H均为1000 mm，管道半径为2.5 mm，螺旋微反应器的曲率δ为0.2，无量纲螺距λ为0.1，雷诺数Re为1000，采用模拟计算，对比研究直通道微反应器与螺旋微反应器的努塞尔数Nu和阻力系数f。为了进一步分析螺旋管内流体流动与传热的强化作用，采用模拟仿真获得螺旋微反应器和直管通道在δ=0.2，λ=0.1，Re=1000 时的速度场和温度场分布。

3 结果分析与讨论

3.1 尺度效应

本研究对不同管径螺旋微反应器内的传热进行了模拟，获得管道半径r对努塞尔数Nu，阻力系数f，流体通量Q和压降Δp的影响规律，模拟计算结果如图5 所示。由图5 可以看出，当管道半径r从0.5 mm 增大到2.5 mm 时，Nu从3.15 不断增大到11.3，变化幅度较大。流动阻力系数f不断增大，在r达到1.5 mm 时流动阻力系数f增大幅度变小，变化的幅度较小。因此，螺旋微反应器的传热性能存在“放大效应”，从努塞尔数Nu的角度来看，螺旋微反应器管道半径r可放大到2.5 mm。此外，随着通道半径的增大，流体的压降Δp逐渐减小，且通量逐渐增大。当管道半径r从0.5 mm增大到2.5 mm 时，在维持高传热性能的同时，流体的压降减小了98.9%，而换热流体通量增大了25 倍，且流体通量和通道半径符合公式Q=0.0056r2。但当管道半径继续增大时，螺旋微反应器对流体流动二次流所产生的影响不断减弱，过大的管径对流体传热效率的提升反而不明显。因此，在管径0.5～2.5 mm 范围对螺旋微反应器进行尺度放大，可在维持较大传热性能的同时，实现压降的降低和通量的放大。

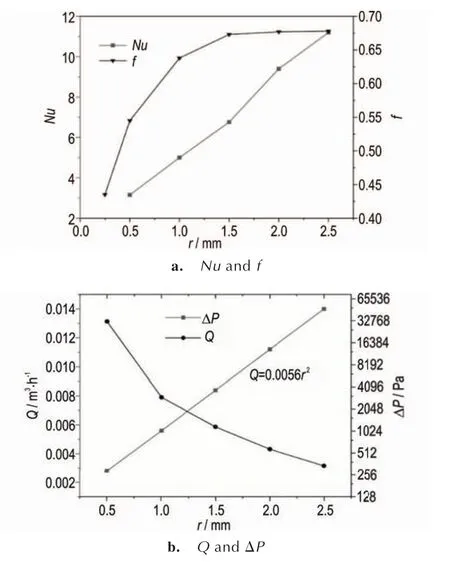
图5 尺寸放大时管径对Nu、f、ΔP 和Q 的影响Fig.5 Impact of pipe diameter on Nu， f， Δp and Q during size expansion

3.2 结构参数对螺旋微反应器传热的影响

3.2.1 曲率对螺旋微反应器传热的影响

本研究对不同曲率δ和雷诺数Re时的传热性能进行了模拟，获得曲率δ和雷诺数Re对努塞尔数Nu和阻力系数f的影响规律，模拟计算结果如图6 所示。层流流动状态下，当雷诺数Re较小时，曲率δ对努塞尔数Nu的影响不大；但随着雷诺数Re的增大，曲率δ对努塞尔数Nu的影响也逐渐增大。在雷诺数一定时，努塞尔数随着曲率δ的变化呈现先增大后减小的趋势。主要因为随着螺旋曲率δ的增大，螺旋半径逐渐减小，螺旋管弯曲程度相对越大，会造成二次流强度逐渐增强，但继续增大曲率δ会促进流体形成层流流动的趋势，致使螺旋管传热效率先增大后减小。曲率δ的变化对阻力系数f的影响较为明显，曲率δ越大，阻力系数f也越大。此外，在相同曲率下，阻力系数随着雷诺数的增高而降低。当曲率增加时，管道的弯曲程度也会随之增加，这会进一步影响微反应器内流体的速度方向和尺寸，从而导致微反应器内流体的阻力系数上升。尽管增大螺旋微反应器的曲率可以强化传热性能，但考虑到曲率为0.4 时，管内的流动阻力较大，因此选择δ=0.2 作为最佳曲率。

图6 曲率δ 对Nu 和f 的影响Fig.6 Influence of curvature on Nu and f

3.2.2 无纲量螺距对螺旋微反应器传热的影响

本研究对不同无纲量螺距λ和雷诺数Re时的传热性能进行了模拟，获得无纲量螺距λ和雷诺数Re对努塞尔数Nu和阻力系数f的影响规律，模拟计算结果如图7 所示。由图7 可以看出，层流状态下，无纲量螺距λ对螺旋微反应器的努塞尔数Nu影响很小，但对阻力系数f的影响较大。随着无纲量螺距λ的增大，螺旋微反应器内的努塞尔数Nu基本保持不变，而阻力系数逐渐增大。此外，增大雷诺数Re时，不同无纲量螺距λ时努塞尔数Nu的变化量逐渐增大，而阻力系数f逐渐减小。在雷诺数Re相同时，λ=0.100 与λ=0.204的阻力系数f基本一样，但当无纲量螺距λ继续增大时，其对螺旋微反应器内的阻力系数f的影响也变大，不利于螺旋管的传热。因此，选择λ=0.1 为最佳无量纲螺距。

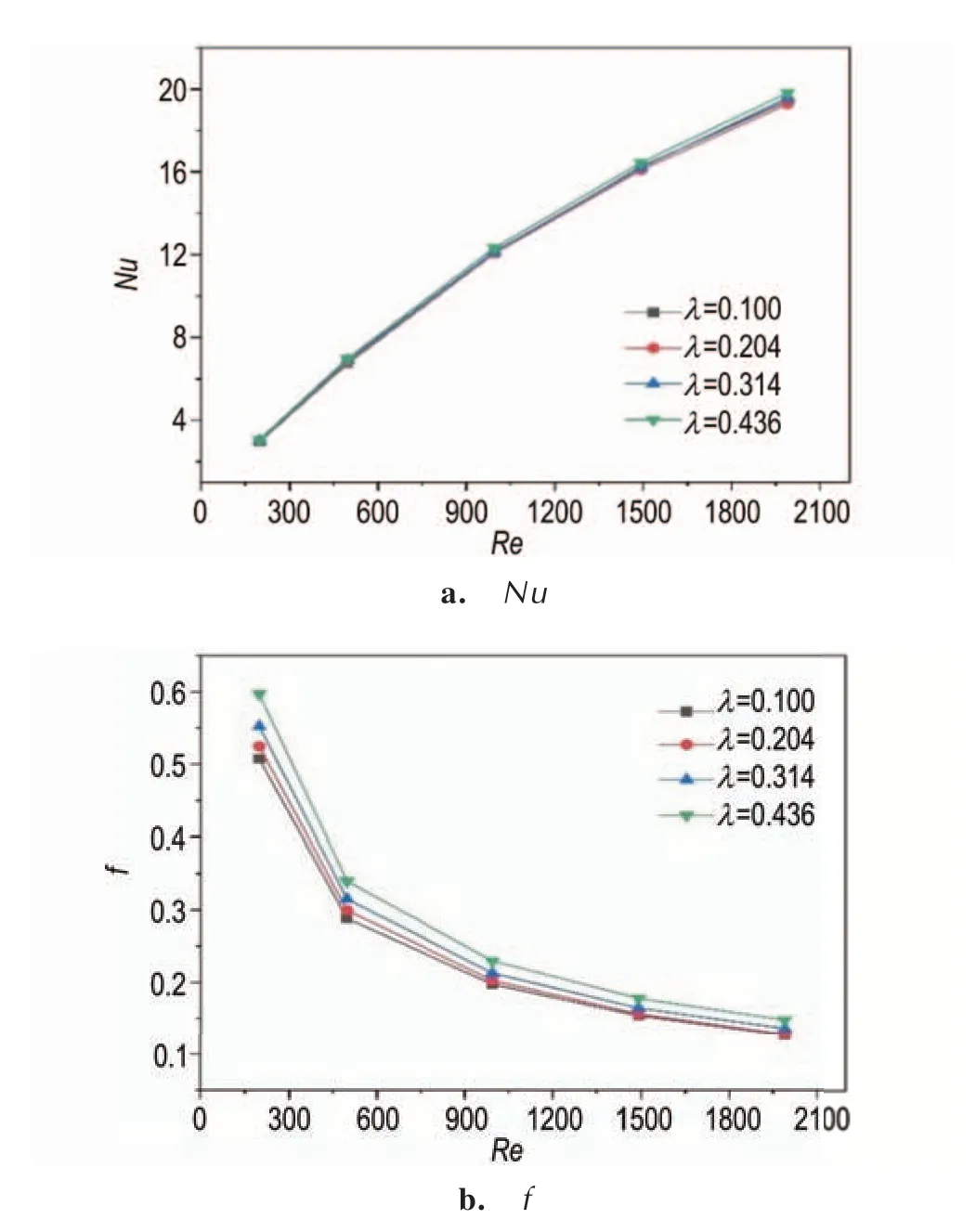
图7 无纲量螺距对Nu 和f 的影响Fig.7 Influence of dimensionless pitch on Nu and f

3.3 直通道与螺旋微反应器对比

3.3.1 传热性能

本研究对直通道和螺旋微反应器的传热性能进行了模拟，获得两种微反应器在不同雷诺数Re时的努塞尔数Nu和阻力系数f，对比直通道与螺旋微反应器的传热性能，考察螺旋微反应器对流体流动与传热的强化作用，模拟计算结果如图8 所示。由图8 可以看出，由于螺旋微反应器比直通道弯曲，增大了流体流动的阻力，导致螺旋管内的阻力系数高于直通道微反应器。同时在较低雷诺数下，螺旋微反应器内的努塞尔数低于直通道的努塞尔数。原因是由于雷诺数较低时，入口处的速度较低，流体在螺旋微反应器内不容易产生二次流，从而没有强化传热性能［34］。当雷诺数大于450 时，螺旋微反应器内的努塞尔数明显高于直通道内的努塞尔数。这是由于螺旋微反应器的弯曲提高了管壁处的流体和管中心的流体的热交换强度，说明在较高层流雷诺数下螺旋微反应器有强化传热性能的能力。但是由于螺旋微反应器比直通道弯曲，增大了流体流动的阻力，导致螺旋管内的阻力系数总是比直管的大。由此可见，螺旋微反应器可以强化传热性能的。

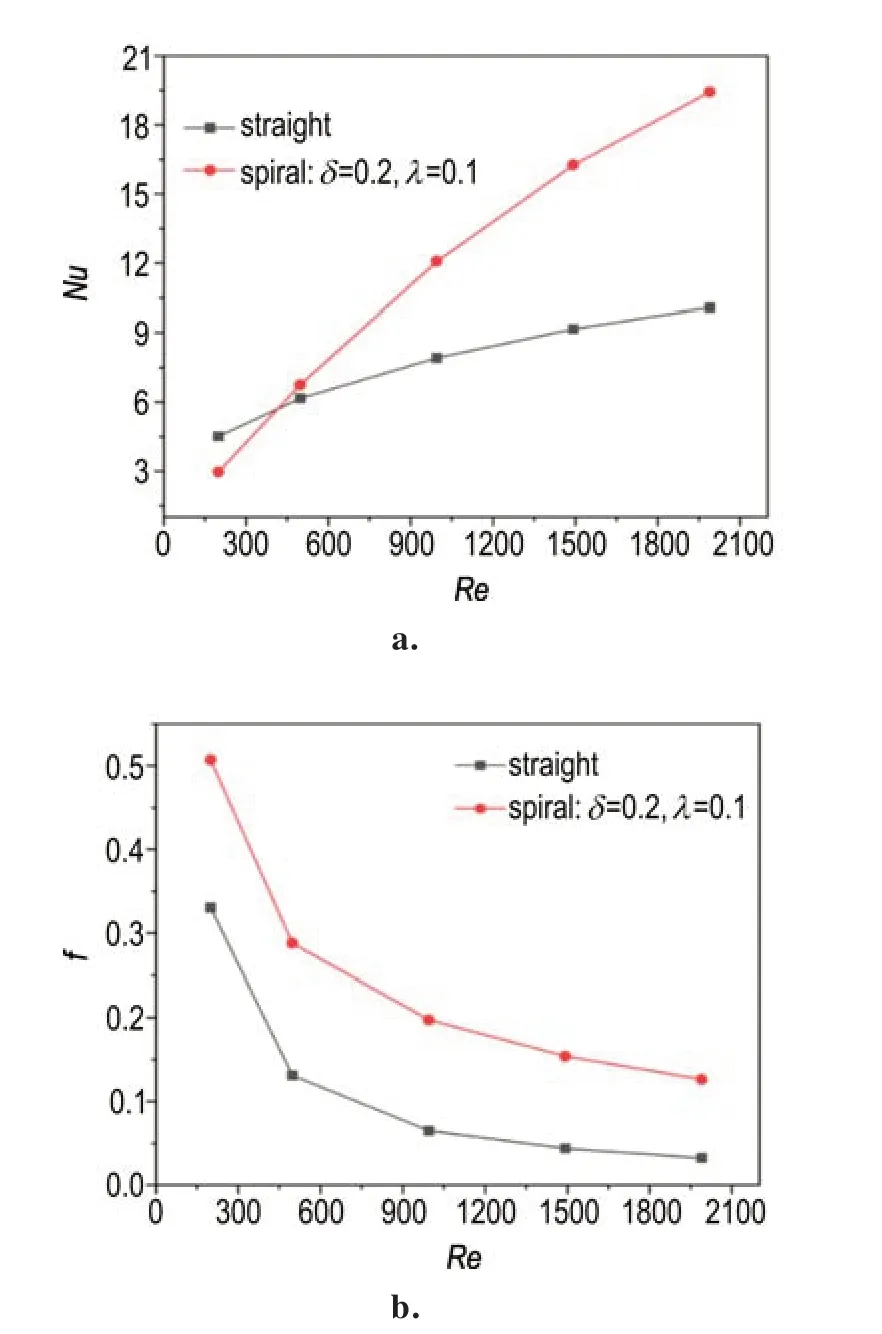
图8 直通道与螺旋微反应器Nu 和f 对比Fig.8 Comparison of Nu and f between straight microreactor and spiral microreactor

直通道与螺旋微反应器的努塞尔数分布云图如图9 所示。由图9 可以看出，直通道与螺旋微反应器均在入口处具有较高的努塞尔数，且随着流体的流动努塞尔数逐渐减小。不同的是，在直通道中的努塞尔数急剧减小，而直通道与螺旋微反应器内的努塞尔数减小的速率较小。原因是由于通道的弯曲强化了螺旋直通道与螺旋微反应器内流体的流动与传热，致使努塞尔数减小缓慢。因此，螺旋微反应器管道的平均努塞尔数比直管大，即螺旋微反应器的传热性能比直通道优。

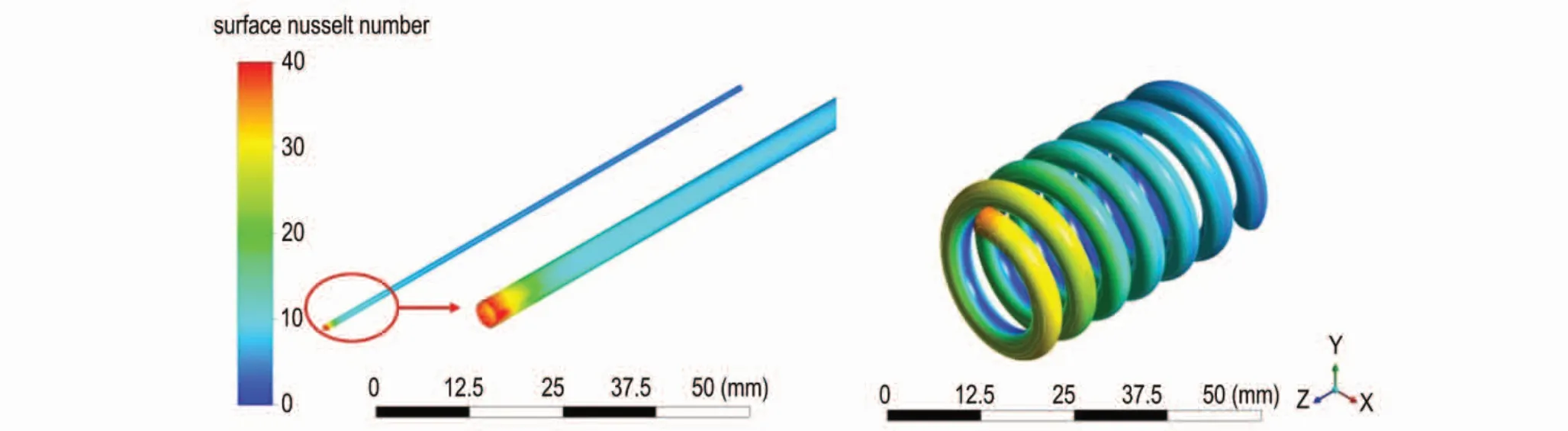
图9 直通道与螺旋微反应器努塞尔数分布云图Fig.9 Nussel number distribution cloud map of straight microreactor and spiral microreactor

3.3.2 速度场和温度场分布

为了进一步分析螺旋管内流体流动与传热的强化作用，采用模拟仿真获得了螺旋微反应器和直管通道在δ=0.2，λ=0.1，Re=1000 时的速度场和温度场分布云图，如图10 和图11 所示。螺旋微反应器是在距离入口处旋转1～6 圈处取得的截面，而直通道是根据螺旋管长度取得截面对应长度处取得的截面。由图10可以看出，直管的温度分布较为均匀，但管中心流体的温度最低，只有管壁处的流体进行了传热。随着管长的增加，逐渐向管中心进行传热，但对于长度为1 m 的直管，其传热还未能达到管中心流体。而螺旋微反应器内的温度不是均匀分布的，一开始管壁周围的温度还较低，但随着螺旋微反应器不断延伸，热量会受到二次流和热边界层的影响，会从螺旋微反应器管壁附近逐渐传递到管中心部位。

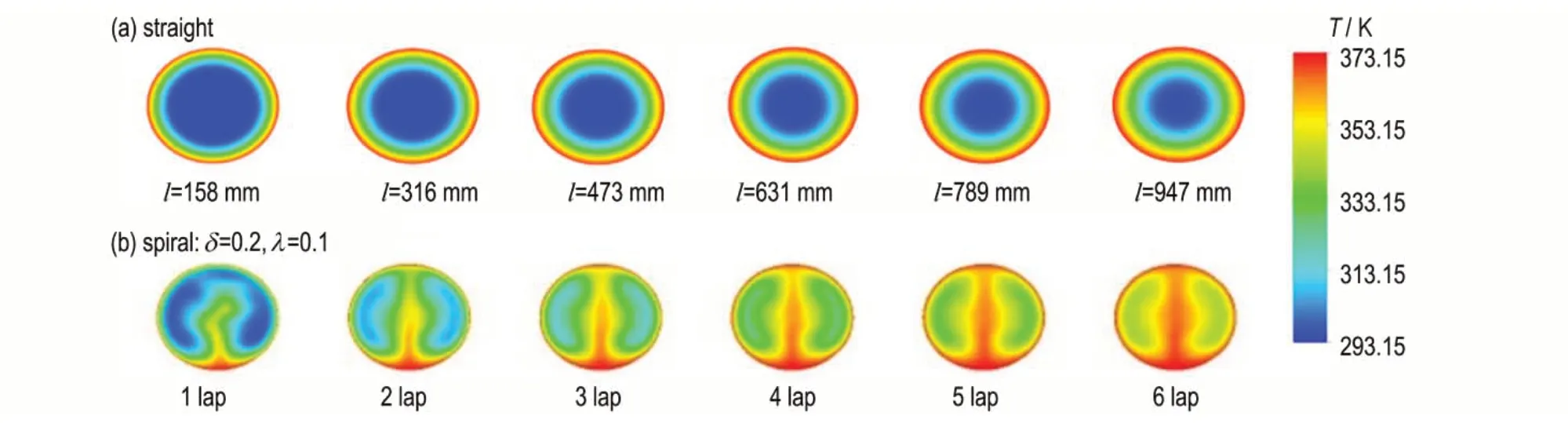
图10 直通道与螺旋微反应器不同截面温度场分布Fig.10 Temperature field distribution in various sections of straight channel and spiral microreactor

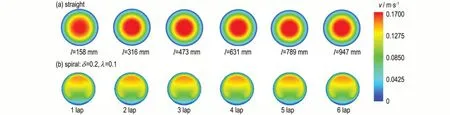
图11 直通道与螺旋微反应器不同截面速度场分布Fig.11 Velocity field distribution in various sections of straight channel and spiral microreactor

由图11 可以看出，直通道的速度分布较为均匀，管中心的速度比管壁周围的速度高，流体在直通道里面流动的速度变化较小。而螺旋微反应器中，速度分布不再均匀，在旋转一圈时的速度分布就呈现内凹的圆弧形状且不再有明显的变化，说明流体已经达到了充分发展的阶段。随着流体在螺旋微反应器中不断流动，离心力对流动流体各点的效果会逐渐加强，二次流产生的效果也会不断加强，使得外侧壁面处的速度大于内侧壁面处的速度。因此，螺旋微反应器具有较高的传质性能，对强化大尺度传热过程提供了巨大潜力。