冷能梯级利用的港口多能微网双层不确定性经济调度

2024-03-26谢应彪章雷其谢长君

电力系统自动化 2024年6期

侯慧，谢应彪，甘铭，赵波，章雷其，谢长君

（1.武汉理工大学自动化学院，湖北省武汉市 430070；2.武汉理工大学深圳研究院，广东省深圳市 518000；3.国网浙江省电力有限公司电力科学研究院，浙江省杭州市 310014）

0 引言

现代港口越来越多地考虑将液化天然气（liquified natural gas，LNG）作为清洁燃料，LNG 在气化时会释放大量清洁无污染的冷能，可结合碳捕集、发电、供冷等多种形式进行冷能利用［1］。此外，港口也将海上风电等可再生能源消纳作为重要的低碳环保考核指标，推进港口能源低碳转型［2］。

目前，关于LNG 冷能利用的研究主要集中于化工领域的热力学分析与评估等方面［3］，针对港口多能微网（multi-energy microgrid，MEMG）能源调度层面的LNG 冷能利用相关研究则较为匮乏。文献［4］将碳捕集电厂与LNG 气化站联合运行，利用LNG 冷能制备液态CO2和干冰，但其制取经济商品的冷能利用方式与能源系统运行调度耦合性较弱。为进一步提升LNG 冷能利用潜力，文献［5］在利用复合能源管道输送LNG 的同时，实现LNG 气化冷能的发电-制冷两级利用，但其未考虑LNG 冷能的负碳排特性，未能有效促进降碳减排。可见，现有研究尚未充分挖掘LNG 冷能利用的低碳灵活性潜力。

针对海上风电不确定性，常用场景法进行刻画。在场景生成方面，文献［6］通过海上风电误差场景与预测值叠加生成风电场景，但未考虑风电预测误差时序相关性，导致场景的风电出力波动性与实际不符［7］。在场景削减方面，传统的场景削减方法如K-中心点聚类、快速前向选择及分层聚类等存在聚类有效性较差等问题［8］。为此，文献［9］提出基于Wasserstein 距离的0-1 规划模型场景削减方法，并构建聚类指标体系以量化场景削减效果及有效性。因此，在进行风电不确定性刻画时，有必要兼顾场景生成对风电出力时序波动性的考虑，以及场景削减对不确定性保留程度的考虑。

在港口MEMG 调度方面，常用随机优化［10］、鲁棒优化［11］等刻画可再生能源如海上风电不确定性。然而，通过两者优势互补、实现经济性与鲁棒性合理权衡的分布鲁棒优化［12］则研究较少。文献［6］采用两阶段分布鲁棒优化为港口MEMG 提供海上风电不确定性风险下兼顾经济性及鲁棒性的日前调度方案。模型预测控制（model predictive control，MPC）的引入，可进一步通过滚动优化、反馈校正等环节实时修正风电预测误差的影响［13］。文献［14］将MPC应用于含岸电的港口能源系统日内调度，以应对岸电负荷、风电出力不确定性。上述研究为港口MEMG 不确定性调度奠定了基础，但均只基于单时间尺度开展，易使单一日前调度方案与实际情况偏差较大、日内调度陷入局部最优等。

综上，本文提出一种考虑LNG 冷能梯级利用的港口MEMG 鲁棒-随机双层不确定性经济调度模型。主要创新点如下:1）考虑冷能利用与电能调度的耦合机理，建立LNG 冷能梯级利用模型与协同碳处理流程，充分挖掘LNG 冷能利用的低碳灵活性潜力；2）探寻风电出力时序波动性的动态变化规律，基于等概率逆变换进行海上风电场景生成，并基于Wasserstein 距离的0-1 规划模型进行场景削减；3）聚焦调度策略经济性与鲁棒性的合理权衡，提出日前分布鲁棒优化-日内滚动随机优化的双层不确定性模型，充分发挥多时间尺度的协同优化效应。

1 含冷能梯级利用的港口MEMG 模型

结合港口MEMG 具体用能特性对不同温区内的LNG 冷能进行梯级利用，可最大化LNG 冷能利用效益。因此，提出含LNG 冷能梯级利用的港口MEMG 模型，如图1 所示。

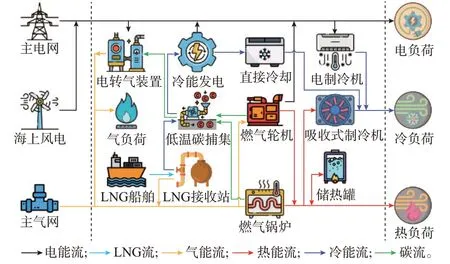
图1 含LNG 冷能梯级利用的港口MEMG 结构Fig.1 Structure of port MEMG with cascade utilization of LNG cold energy

LNG 从-162 ℃液化温度升至25 ℃使用温度时，将释放大量冷能，结合港口MEMG 具体用能特性对不同温区内LNG 冷能进行梯级利用，可最大化LNG 冷能的利用效率。因此，提出应用于港口MEMG 的低温碳捕集（深冷）-冷能发电（中冷）-直接冷却（浅冷）三级冷能梯级利用模型，如图2 所示。图中:一级利用低温碳捕集用于减少燃气轮机、燃气锅炉等灵活性资源的碳排放；二级利用冷能发电用于供给电负荷；三级利用直接冷却用于供给冷负荷，以进一步提高冷能利用率。LNG 气化后的天然气用于供给气负荷。

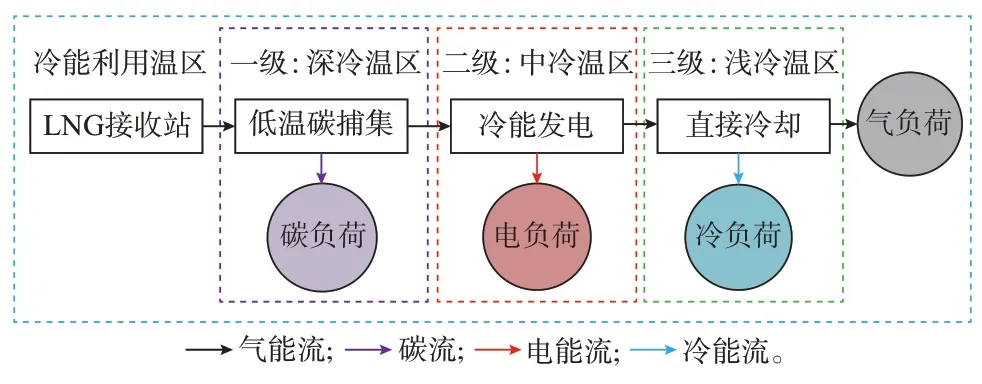
图2 LNG 接收站冷能梯级利用示意图Fig.2 Schematic diagram of cold energy cascade utilization in LNG receiving station

1.1 冷能梯级利用建模

LNG 接收站在接纳、存储LNG 船舶运输的LNG 之后，需通过LNG 气化获得天然气以供给气负荷，如式（1）所示。同时，LNG 接收站应满足存储容量及气化功率限制，相应约束如式（2）、式（3）所示。

式中:S、S分别为t时刻、t-1 时刻LNG 储罐的储气状态，并以荷电状态（state of charge，SOC）泛指；Gngt为t时刻LNG 接收站的气化功率；ςng为天然气热值；vlng/ng为同等质量下LNG（液态）与天然气（气态）的体积比值，取值为1/625；λlng为LNG 储罐的容量；Δt为调度步长；Slng，max、Slng，min分别为LNG 储罐的SOC 上限、下限；Gng，max为LNG 接收站的气化功率上限。

LNG 气化过程中，可回收利用的冷能功率与LNG 接收站气化功率的关系如式（4）所示。

式中:L为t时刻LNG 气化过程中可回收利用的冷能功率；mng为天然气体积/质量比；ηlng为LNG 冷能回收利用效率系数；L为t时刻用于低温碳捕集的高品位冷能功率；L为t时刻用于冷能发电的中品位冷能功率；L为t时刻用于直接冷却的低品位冷能功率。

燃气轮机、燃气锅炉会排放大量CO2，若通过深冷温区的高品位冷能进行低温碳捕集［15］，可有效降低碳排成本。LNG 低温碳捕集模型如式（5）所示。

式中:C为t时刻低温碳捕集到的碳量，碳量可视为碳的流量，单位为kg/h；ηlng，c为低温碳捕集效率，取值为6 kg/（kW·h）；φlng，c为用于低温碳捕集的高品位冷能占比。

在经低温碳捕集消耗高品位冷能后，以海水作为热源、以LNG 作为冷源，实现冷能发电以充分利用中冷温区的中品位LNG 冷能。LNG 冷能发电模型如式（6）所示。

式中:P为t时刻冷能发电功率；ηlng，p为冷能发电效率；φlng，p为用于冷能发电的中品位冷能占比。

对于剩余低品位LNG 冷能，可用于供给低温冷库、冷藏集装箱等港口MEMG 冷负荷。LNG 供冷模型如式（7）所示。

式中:φlng，l为用于直接冷却的低品位冷能占比。

1.2 碳存储与利用建模

低温碳捕集后，还需进行碳的存储、利用与封存，可视为图2 中的碳负荷。其中，碳存储对捕集到的CO2进行存储，在电转气装置需碳原料时进行供给，碳存储模型如式（8）—式（11）所示；碳利用将CO2作为电转气的碳原料，以降低成本，碳利用模型如式（12）—式（14）所示；碳封存对无法进行碳利用的CO2进行封存，以避免非必要碳排放，碳封存模型如式（15）所示；整体碳流平衡约束如式（16）、式（17）所示。

2 海上风电不确定性刻画

2.1 基于等概率逆变换的场景生成

为刻画海上风电的不确定性，基于等概率逆变换生成任意数量符合预测误差时序相关性、出力波动性的风电场景。

建立预测箱对预测误差累积经验概率分布进行拟合，如式（18）所示。

式（19）中，均值列向量μerr为T维0 向量，协方差矩阵可展开如式（20）所示。可采用指数型函数法［16］来描述两个不同时刻随机误差向量之间协方差与时间间隔的相关性，则协方差矩阵中各元素值可通过式（21）进行估计。

式中:元素σ为m时刻随机误差变量σ和n时刻随机误差变量σ的协方差；ε为波动范围参数，需根据风电出力的实际波动性进行确定。

在获得随机误差向量概率密度函数的基础上，通过等概率逆变换将随机误差向量eerr映射到预测误差向量Perr上，使预测误差向量具有时序相关性。等概率逆变换过程［17］可以描述为式（22）。

式中:Ferr，2(·)为随机误差向量eerr的累积概率分布函数；Ferr，1(·)为预测误差向量Perr的累积经验概率分布函数，F(·)为Ferr，1(·)对应的反函数。

将预测误差向量Perr与预测值向量Pfor叠加得到风电原始场景Psce，如式（23）所示。

为确定最佳的波动范围参数ε，以及生成符合风电出力实际波动性的场景，采用波动拟合指标Iε量化场景风电出力波动与实际风电出力波动的拟合差异，如式（24）所示。

式中:X、[X]分别为用于概率密度等距抽样的样本数量、样本点集合；fpdf，1(·)、fpdf，2(·)分别为实际、场景的风电出力波动概率密度。

风电出力波动概率密度函数采用t-location scale 分布拟合，如式（25）所示。

式中:Γ(·)为伽马函数；μt-loc为位置参数；σt-loc为比例参数；vt-loc为形状参数。

2.2 基于0-1 规划模型的场景削减

场景削减的目标是确保场景削减前后对应的不确定性优化问题的优化结果相差最小，即不确定性优化问题基于典型场景计算的目标函数值与基于原始场景计算的目标函数值相差最小［18］。目标函数差值定义如式（26）所示。

式中:ρ0(·)为基于不同场景计算的目标函数值；P1为原始场景表征的概率分布，p1为对应的不确定变量；P2为典型场景表征的概率分布，p2为对应的不确定变量；sup为上确界函数；f0(·)为不确定性优化问题的目标函数。

式（26）的对偶形式即为Wasserstein 距离，如式（27）所示。

式中:ρW(P1，P2)为概率分布P1与概率分布P2间的Wasserstein 距离；inf为下确界函数；ρ(·)为基础距离测度；Q为联合分布集合；Q(·)为P1与P2的联合分布。

结合Wasserstein 距离，场景削减的目标可重新定义为:在给定的典型场景数S2下，寻找最优典型场景集[S2]，使其表征的离散概率分布P2与原始场景集[S1]表征的离散概率分布P1间的Wasserstein距离最小。因此，场景削减的过程可以视作一个典型的选址-分配双层优化模型:下层模型在给定典型场景数的情况下，从原始场景集中选出部分场景作为典型场景sj；上层模型在得到典型场景的情况下，根据就近原则将初始场景分配到各个典型场景中，并计算典型场景概率pj。通过引入0-1 变量，可将原始场景与典型场景间Wasserstein 距离转化为0-1 规划模型［9］，如式（28）所示。

式中:ϖi，j为0-1 场景分配变量，取值为1 时代表原始场景si被分配至典型场景sj，为0 时代表未被分配；ci为0-1 场景选择变量，取值为1 时代表原始场景si被选择为典型场景，为0 时代表未被选择；st，i、st，j分别为原始场景si、典型场景sj在t时刻的值；第1 行约束用于确保单个原始场景不会被重复分配到多个典型场景中；第2 行约束用于确保选择的典型场景数等于给定值S2；第3 行约束用于确保仅对被选中作为典型场景进行场景分配。

典型场景概率pj可通过式（29）的计算结果求得，场景概率不为0 的场景即为最终的典型场景。

为捕获场景风电出力不确定性等外部特征，采用不确定性指标［9］作为外部评价指标来评价场景削减对不确定性信息的保留程度，如式（30）所示。

式中:IUN为正向指标，即指标数值越大，代表不确定信息保留程度越高；Pj，t为典型场景sj的t时刻风电出力；P为原始场景集t时刻风电出力的平均值。

传统场景削减内部评价指标采用欧氏距离从场景内部几何特征对场景削减效果进行评价，但几何特征无法有效描述场景的时序特征，难以获取有效的最佳典型场景数。考虑到风电场景实际表征的是风电不确定性的离散概率分布，相比于欧氏距离，Wasserstein 距离能更好地描述概率分布间距离，以减少场景削减对不确定性优化问题的影响。因此，采用Wasserstein 距离作为内部评价指标。

3 鲁棒-随机双层不确定性经济调度

3.1 双层不确定性调度框架

为适应风电预测误差随时间尺度增加而增大的固有特性，建立港口MEMG 鲁棒-随机双层不确定性调度框架。其中，上层考虑日前长时间尺度预测精度较低，通过分布鲁棒优化保证预调度决策鲁棒性，并将预调度决策作为下层滚动随机优化的参考值，避免下层陷入局部最优；下层考虑日内短时间尺度预测精度较高，通过随机优化保证滚动调度决策经济性［19］，并结合MPC 进行滚动优化，及时消除预测误差带来的影响。双层调度框架如图3 所示，具体优化过程如附录A 图A1 所示。

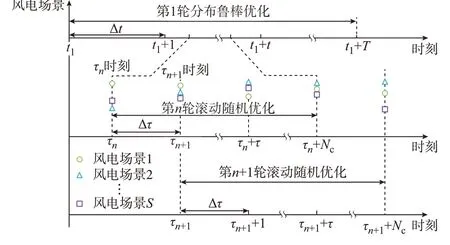
图3 鲁棒-随机双层不确定性经济调度框架示意图Fig.3 Schematic diagram of framework for robuststochastic bi-layer uncertainty economic scheduling

在上层优化调度中，仅进行单轮日前长时间尺度分布鲁棒优化。假设优化初始时刻为t1，时间间隔为Δt，预测时域及控制时域含有T个时间间隔，即预测时域及控制时域均为t1至t1+T。在控制时域内进行分布鲁棒优化，通过模糊集刻画预测时域内风电预测误差不确定性，求取最优预调度决策x=[x(t1+1|t1)，x(t1+2|t1)，…，x(t1+T|t1)]T，将其作为下层滚动随机优化调度的参考，下层跟踪修正上层预调度决策。对于单轮分布鲁棒优化，预调度决策可写为简洁形式x=[x1，x2，…，xt，…，xT]T，便于后续分布鲁棒优化模型建立。

在下层优化调度中，进行多轮日内短时间尺度滚动随机优化。假设第n轮滚动优化初始时刻为τn，时间间隔为Δt，预测时域及控制时域含有Nc个时间间隔，即预测时域及控制时域均为τn至τn+Nc。在初始时刻τn执行上一轮初始时刻τn-1下发的滚动调度决策u(τn-1+1|τn-1)，然后在控制时域内进行随机优化，通过场景刻画预测时域内风电预测误差不确定性，求取控制时域内最优滚动调度决策u=[u(τn+ 1|τn)，u(τn+ 2|τn)，…，u(τn+Nc|τn)]T，仅下发第1 个滚动调度决策u(τn+1|τn)作为下一轮初始时刻τn+1执行的调度决策，重复以上过程。对于任意轮滚动随机优化，滚动调度决策可写为简洁形式u=[u1，u2，…，uτ，…，uNc]T，便于后续优化模型建立。

3.2 上层分布鲁棒优化调度

上层为日前-日内两阶段分布鲁棒优化调度，日前阶段基于风电出力的预测值进行日前预调度，日内阶段基于风电出力的日前预测误差历史数据为日前阶段预调度不同决策造成的再调度成本提供期望风险，输出日前阶段预调度决策作为下层滚动随机优化调度的参考值。其中，所依赖的Wasserstein 模糊集构建方法、误差区间获取方法以及两阶段分布鲁棒优化模型求解方法详见文献［6］，所依赖的风电误差场景由第2 章获取。

1）目标函数

上层分布鲁棒优化调度在Wasserstein 模糊集F 的风电预测误差最恶劣分布P͂下，使日前阶段预调度成本cTx与日内阶段期望再调度成本EP͂(dTy)总和最小，如式（31）所示。其中，预调度决策x、再调度决策y的具体变量构成见附录A 式（A1）。

式中:c为预调度决策x对应系数列向量；d为再调度决策y对应系数列向量；C为t时刻主网交互预调度成本；C为t时刻碳排放预调度成本；C为t时刻主网功率波动惩罚成本；Dmaint为t时刻主网交互再调度成本；D为t时刻碳排放再调度成本；D为t时刻弃风、削负荷惩罚成本。

上述成本计算方式如式（32）所示。

式中:c、c分别为t时刻MEMG 向主电网购电、售电日前价格；P、P分别为t时刻MEMG 向主电网购电、售电功率；cg，buy为MEMG 向主气网购气价格；G为t时刻MEMG 向主气网购气功率；cf为碳封存价格；cco2为碳税价格，取值为0.25 元/kg；δp，co2为主电网碳排放系数；cvary为主电网功率波动惩罚系数；P为t时刻主电网波动功率；分别为t时刻MEMG 向主电网购电、售电日内价格；分别为t时刻向主电网购电、售电调整功率；G͂ buyt为t时刻向主气网购气调整功率；分别为t时刻碳封存、碳排放调整量；cwt、cload分别为弃风、削负荷惩罚系数分别为t时刻弃风、削负荷调整功率。

2）日前阶段预调度约束

LNG 接收站、冷能梯级利用、碳存储、碳利用、碳封存、碳流平衡的预调度约束如式（1）—式（17）所示。冷、热、电、气功率平衡的预调度约束如式（33）—式（36）所示。燃气轮机、燃气锅炉、吸收式制冷机、电制冷机、储热罐、主电网等通用模型预调度约束与再调度约束参考文献［6］，此处不再赘述。

3）日内阶段再调度约束

在日前预调度的基础上，日内阶段再调度主要是基于历史预测误差数据为日前阶段预调度不同决策提供对应的期望最优再调度成本。因此，两阶段分布鲁棒优化仍属于日前调度邻域。其中，LNG 接收站、冷能梯级利用、碳存储、碳利用、碳封存、碳流平衡、弃风、削负荷及功率平衡的再调度约束见附录A 式（A2）—式（A22）。

3.3 下层滚动随机优化调度

为充分利用风电预测误差不确定性信息，下层采用随机优化代替传统MPC 中的确定性优化，从而进行滚动随机优化，并根据获得的日前分布鲁棒优化预调度决策、风电场景及其场景概率，以控制时域内成本期望和最小为优化目标，计及不同场景内的非预期性约束构建随机优化模型，求取控制时域内期望最优的滚动调度决策，并仅下发执行第1 个滚动调度决策，平移预测时域及控制时域。重复上述过程进行滚动优化，具体流程图见附录A 图A2。

1）日内阶段滚动调度目标函数

滚动随机优化调度在日内阶段跟踪并修正日前阶段预调度决策，目标为求取使控制时域Nc（初始时刻为τn）内各场景s下滚动调度成本、滚动调度决策偏离预调度决策惩罚成本期望之和最小的滚动调度决策u，其目标函数如式（37）所示。

2）日内阶段滚动调度约束条件

燃气轮机、燃气锅炉、吸收式制冷机、电制冷机、储热罐、LNG 接收站、冷能梯级利用、储碳罐、碳利用、碳封存、碳流平衡及冷、热、气功率平衡的滚动调度约束与预调度相同，但要求在日内τ时刻及任意场景s下均可行，且不包含调度周期始末端SOC 一致性约束。而弃风、削负荷、电功率平衡、主电网滚动调度约束如式（38）—式（45）所示。

日内阶段滚动调度还应满足非预期性约束，即在任意风电场景s下，控制时域Nc内求取的第1 个滚动调度决策均应一致，如式（46）所示。

式中:us，τ=1为场景s下控制时域内求取的第1 个滚动调度决策。

4 仿真结果与分析

4.1 仿真参数设置

储热罐、燃气轮机、燃气锅炉、吸收式制冷机、电制冷机等设备参数以及碳排放参数、海上风电、主电网、主气网、电负荷等相应成本系数参考文献［6］，为匹配冷能梯级利用与适应日内短时间尺度，将燃气轮机的上/下行爬坡速率上限调至1 200 kW/h，电制冷机、吸收式制冷机、储热罐的功率上限分别调至2 800、1 500、1 800 kW，储热罐的容量调至50 000 kW·h，见附录A 表A1。其余设备参数如表1 所示，气负荷参考文献［5］，风电日前预测误差历史数据、电负荷、热负荷、冷负荷参考文献［6］，其中，冷负荷在文献［6］基础上增加3 000 kW，以便与冷能梯级利用相匹配。调度周期设为当日08:00—次日08:00，上层分布鲁棒优化调度每24 h 执行1 次，间隔为1 h，下层滚动随机优化调度每4 h 执行1 次，间隔为0.25 h。最后，利用RSOME 工具箱调用Gurobi 求解器计算。

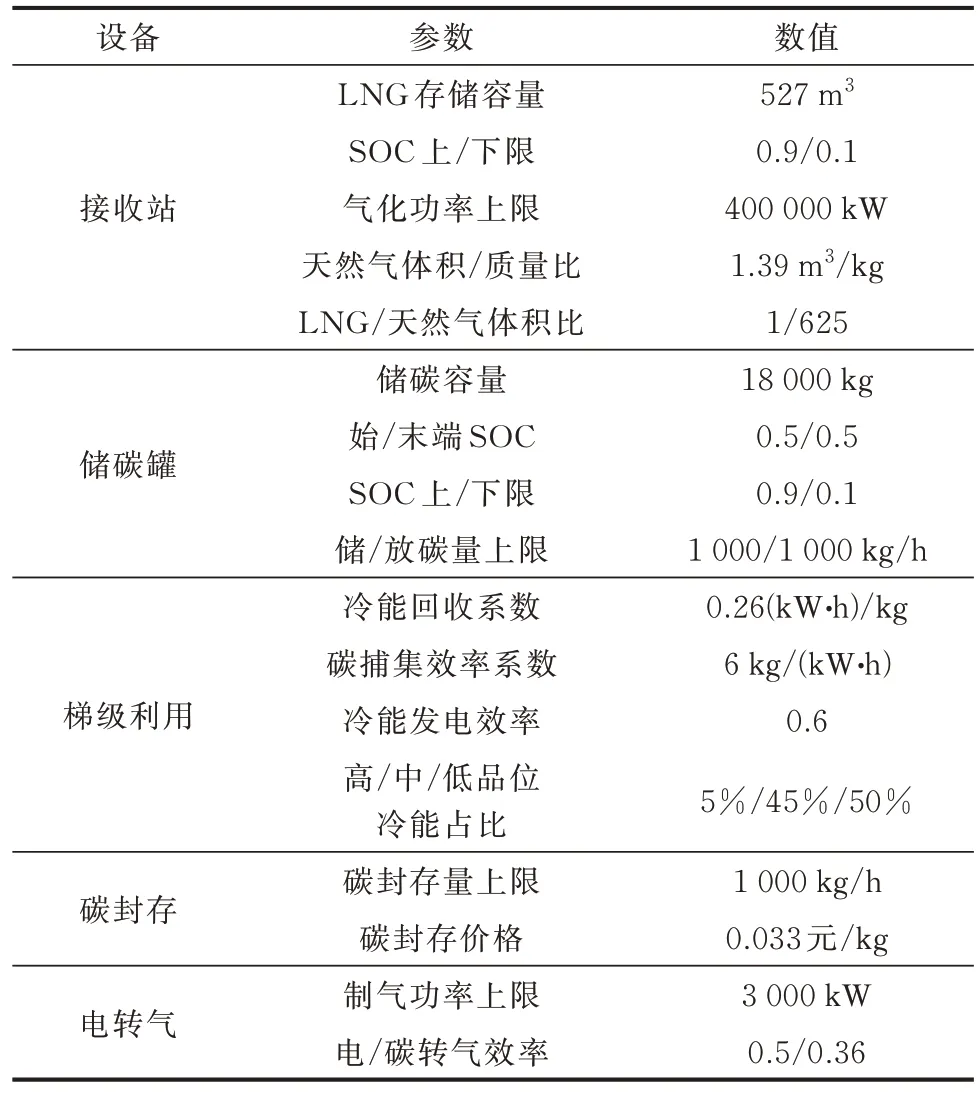
表1 含LNG 冷能梯级利用的港口MEMG 设备参数Table 1 Parameters of port MEMG equipment with LNG cold energy cascade utilization

MPC 只关注预测功能，而不关注预测形式，且本文研究重点为调度而非预测，故采用Tennet 运营商［20］预测周期的初始4 h 预测值、实测值模拟风电日内预测误差历史数据，并按比例缩小使用，弥补了目前MPC 研究［21］多采用正态分布模拟预测误差数据不符合实际的不足。

4.2 场景生成与削减有效性分析

进行等概率逆变换场景生成时，需对最佳波动范围参数ε进行确定。不同波动范围参数下的波动拟合指标见附录A 图A3。由图可知，波动范围参数取8 时可认为所生成场景的波动性与实际风电波动性最为符合，并在此参数下进行等概率逆变换，生成400 个风电场景见附录A 图A4。可以看出，风电实测值均处于等概率逆变换所生成的风电场景范围内，65%置信区间即可覆盖风电实测值，各个场景的风电出力均较平滑、不存在无序波动，且风电出力的变化趋势与预测值变化趋势接近。

为验证0-1 规划模型场景削减的有效性，将其与K-中心点聚类、分层聚类、快速前向选择等传统场景削减方法进行对比。风电不确定性指标对比结果、Wasserstein 距离对比结果见附录A 图A5。其中，由图A5（a）可知，风电不确定性指标先急剧增加，当典型场景数大于4 时，风电不确定性指标变化趋于平缓，表明最佳的典型场景数为4。同时，当典型场景数大于等于4 时，0-1 规划模型在风电不确定性指标方面均优于其他3 种场景削减方法。由图A5（b）可知，0-1 规划模型在Wasserstein 距离方面始终优于其他3 种场景削减方法。同时，场景数为4 前后的Wasserstein 距离斜率发生改变，表明场景数大于4 时通过增加场景来减少Wasserstein 距离的效果弱于场景数小于4 时。综合考虑风电不确定性外部评价指标、Wasserstein 距离内部评价指标的评价结果，将最佳典型场景数设为4。最佳典型场景数下的日前风电典型场景及其场景概率如图4 所示。

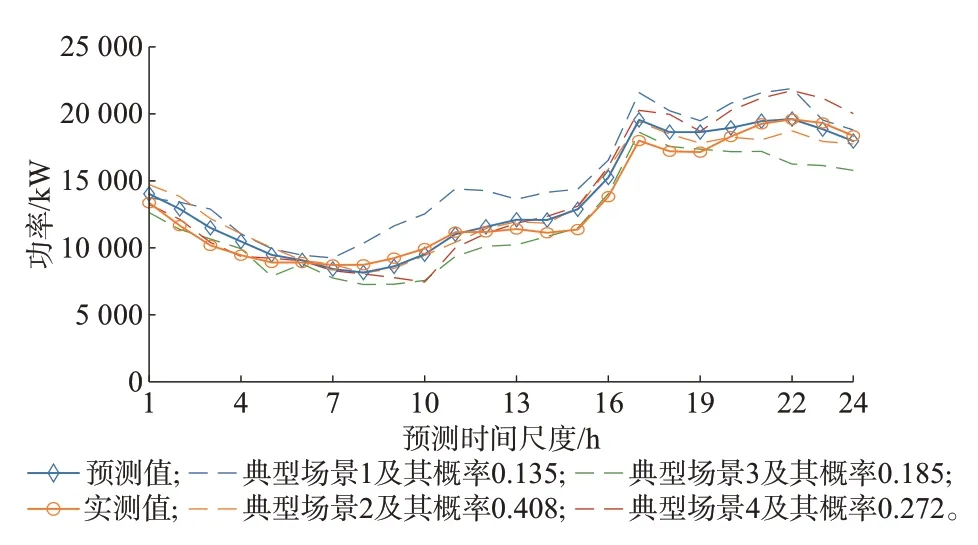
图4 日前风电典型场景及其场景概率Fig.4 Typical scenarios and their probabilities for dayahead wind power

由图4 可知，场景数为4 时典型场景能以较小的场景数覆盖风电实测值的波动范围，从而兼顾不确定性拟合精度和求解效率。日内场景获取流程与日前相同，所获场景见附录A 图A6。基于所生成的日前、日内风电场景，计算两者在65%置信水平下的区间宽度。由附录A 图A6 可知，相比于日前，日内区间宽度始终稳定在较低水平。这表明日内短时间尺度能够提供可信度更高的不确定性信息，避免日前长时间尺度的误差累积。

4.3 调度结果及日内修正情况分析

为对比分析所提鲁棒-随机双层不确定性经济调度模型的可行性及有效性，设置如下4 种对比方案:

方案1:上层分布鲁棒优化调度与下层滚动随机优化调度进行协同优化，滚动下发日内阶段滚动调度决策；

方案2:直接下发分布鲁棒优化日前阶段预调度决策，预测误差引起的日内阶段功率不平衡量全部由主电网、弃风及削负荷进行平抑；

方案3:上层采用鲁棒优化调度，与下层滚动随机优化调度进行协同优化；

方案4:上层采用随机优化调度，与下层滚动随机优化调度进行协同优化。

4 种对比方案的实际调度成本如表2 所示。

表2 4 种对比方案的实际调度成本Table 2 Actual scheduling costs for four comparative schemes

由表2 可知，方案2 直接下发日前预调度决策，港口MEMG 仅能依赖主电网调节灵活性来平抑预测误差，导致日内购售电、功率波动成本显著提升。方案1、3、4 碳排成本的削减，说明其在日内能通过调用燃气轮机、燃气锅炉等本地灵活性资源来平抑预测误差，避免向具有高碳排的主电网进行购电。上述结果表明，采用下层滚动随机优化调度跟踪并修正上层预调度决策，能有效应对预测误差影响。

在采用双层调度框架的方案1、3、4 中:

1）方案4 在日前盲目追求经济性，导致能源储备不足，进而在日内进行大量购电、购气，并造成失负荷。这表明日前采用随机优化难以适应预测精度较低的长时间尺度调度，且难以保证负荷的可靠供应。

2）方案3 虽然解决了随机优化过于乐观所导致的弃风、削负荷及抗风险能力弱等缺陷，但其日前大量能源储备并不符合港口MEMG 实际用能需求，过于追求鲁棒性而导致实际调度成本最高、经济性最差。

3）方案1 在碳排、波动、弃风、削负荷、实际调度成本等多个方面均优于方案3、4，表明上层采用分布鲁棒优化能有效避免随机优化抗风险能力弱、鲁棒优化过于保守的问题。同时，方案1 在日内与主电网功率交互量最低，表明分布鲁棒优化所获预调度决策更符合日前长时间尺度的风电不确定性，避免对日前阶段预调度决策过多的日内调整。

在对比验证了所提鲁棒-随机双层不确定性经济调度模型可行性及有效性的基础上，对其调度结果进行具体分析。其中，负荷供需情况见附录A 图A7。结合图A7（a）、（b）可知，在10:00—21:00 时段内，港口MEMG 的电负荷需求、电价均较高，风电出力较低，通过冷能发电以提高供电能力；同时，燃气轮机运行会产生大量碳排放，通过低温碳捕集以降低碳排成本，但受限于单位时间内碳封存量限制，通过储碳罐将碳捕集到的碳量向后续时段转移。在24:00—次日08:00 时段内，港口MEMG 的电负荷需求、电价均较低，风电出力水平较高，通过电转气装置进行碳利用、消纳过剩的风电出力，储碳罐大量放碳以供给电转气装置、碳封存；结合图A7（b）、（c）、（d）可知，在10:00—21:00 时段内，风电出力小于电负荷，利用直接冷却保证冷负荷需求，削减用电高峰时段的电负荷；同时，多余的热量通过储热罐储热转移到23:00—次日08:00 时段。由图A7（e）可知，LNG 接收站的LNG 气化主要集中于10:00—21:00 时段内，这是由于LNG 接收站在单个调度周期内的LNG 气化量存在上限，为高效利用有限的LNG 冷能，需按照港口MEMG 的实际用能需求进行LNG 气化。

将日内滚动调度对日前预调度的跟踪、修正情况进行具体分析，如图5 所示。

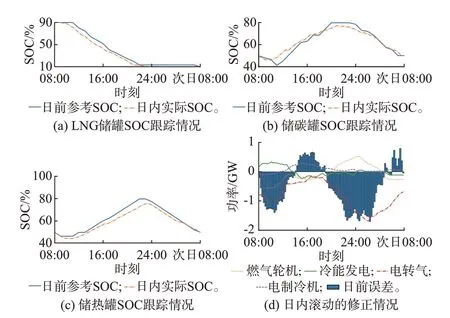
图5 日内滚动调度对日前调度的跟踪与修正情况Fig.5 Tracking and adjustment of intra-day rolling scheduling against day-ahead scheduling

由图5（a）、（b）、（c）可知，储碳罐、储热罐、LNG储罐的日内实际SOC 均能较好地跟踪日前参考SOC，避免日内滚动调度陷入局部最优。由图5（d）可知，在08:00—14:00、19:00—次日08:00 时段内，电转气装置等耗电设备减少出力，而冷能发电或燃气轮机等发电设备增加出力，以补偿日前误差负值（风电日内实测值小于日前预测值）。在14:00—19:00、05:00—08:00 时段内，燃气轮机、冷能发电等发电设备减少出力，而电制冷机等耗电设备增加出力，以补偿日前误差正值（风电日内实测值大于日前预测值）。因此，日内滚动调度能有效利用本地灵活性资源修正日前预调度决策，实时补偿预测误差，并减少对主电网、弃风、削负荷等调节灵活性的依赖。

4.4 冷能梯级利用应用效能分析

为验证分析冷能梯级利用与协同碳处理应用效能，设置如下5 种对比方案:

方案1:回收的LNG 冷能用于直接冷却；

方案2:回收的LNG 冷能用于直接冷却、冷能发电；

方案3:回收的LNG 冷能用于直接冷却、冷能发电及低温碳捕集；方案4:考虑冷能梯级利用，但不考虑碳存储；方案5:考虑冷能梯级利用，但不考虑电转气的碳利用。

方案1、2、3 用于分析冷能梯级利用的应用效能，方案4、5、6 用于分析低温碳捕集与碳存储、碳利用的协同效能。5 种方案对比结果如表3 所示。

表3 冷能梯级利用应用效能分析结果Table 3 Analysis results of application efficiency of cold energy cascade utilization

对比方案1 与方案3 可知，方案1 未利用LNG冷能发电、低温碳捕集，导致实际调度成本提升了26.12%，体现在日前及日内购售电成本、碳排成本的增加；对比方案2 与方案3 可知，方案2 未利用LNG 冷能进行低温碳捕集，导致实际调度成本提升了6.13%，成本的增加体现在碳排成本方面。同时，方案2 相比于方案1 考虑了LNG 冷能发电，避免了大量失负荷成本与购电成本，提高了港口MEMG的供电灵活性。

对比方案3 与方案4 可知，方案4 未考虑碳存储导致实际调度成本提升了5.92%。其中，碳排成本的增加是由于电转气装置仅能利用当前风电富余时刻捕集到的CO2，无法通过碳存储获得其他时刻的CO2，导致其他时刻CO2无法得到及时消纳；失负荷、日前购售电成本的增加是由于燃气轮机排放的CO2受限于当前时刻碳封存量限制，且无法通过碳存储转移到风电富余时刻进行电转气消纳，进而赋予燃气轮机高碳排属性，导致决策更倾向于向主电网购电或失负荷。对比方案3 与方案5 可知，方案5未考虑电转气的碳利用导致实际调度成本提升了10.85%。其中，大量弃风是由于风电富余部分已超出主电网的调节灵活性，且无法通过电转气装置消纳；同时，缺少电转气装置进行碳利用，且无法通过减少电转气装置日内出力来补偿日前误差负值，仅能通过向主电网购电进行补偿，导致碳排、碳封存、日内购售电成本的增加。