量子计算技术在新型电力系统决策优化中的应用

李知艺，许 悦，韩旭涛

（浙江大学电气工程学院，浙江省杭州市 310027）

0 引言

“双碳”政策推行以来，能源电力行业迎来了前所未有的发展机遇。据中国国家能源局统计，截至2023 年9 月，全国总发电装机容量达2.791 GW，其中，以风、光为首的新能源装机容量达965 MW，同比增长29.16%，占比已经超过34%［1］。电力系统正从以化石能源发电为绝对主导的简单电力系统向多种新能源主体共同参与的新型电力系统转变［2］。

新型电力系统具有节点规模庞大［3］、源荷类型多样［4］和网架结构复杂［5］等特点。因此，在规划设计、运行调度以及市场决策等问题的计算复杂度逐步提高。例如，大量不同类型的分布式能源接入电网导致了最优化模型中决策变量类型和约束条件数量的激增；电网拓扑复杂度的提升可能导致目标函数和约束条件在数学表示上的复杂化。新型电力系统优化问题多为混合整数规划（mixed-integer programming，MIP）问题［6］，MIP 问题在数学上属于非确定性多项式困难（non-deterministic polynomial hard，NP-hard）问题［7］，即当求解对象规模较大时，算法不可避免地陷入“维数灾”，计算时间呈现指数级增长［8］。因此，基于经典计算机的决策技术将无法满足新型电力系统运行的要求，耗时的求解过程将导致电力系统调度命令无法及时下发，使电力系统长期运行在一个高损耗、低收益的状态，甚至在出现极端事件的情况下，无法迅速从故障中恢复［9］。综上，在新型电力系统持续发展的情况下，能否找到一种新型计算体系以实现高效、精准的决策优化，是能源电力行业面临的难点。

近年来，量子计算领域取得的一系列突破［10］使应用量子计算机求解经典计算机难以求解的问题成为可能，量子优化算法［11］的概念被提出并率先在量子化学［12］、凝聚态物理［13］以及离散数学［14］等领域获得了广泛应用。量子计算是一种利用量子态的属性（如叠加、纠缠和相干）执行运算过程的新兴技术。量子优化算法利用量子计算机对量子比特进行操控，以量子演化的方式进行寻优。相比于经典优化算法，量子优化算法在求解效率上具有明显优势，对于新型电力系统中特定的MIP 问题，量子计算机理论上可在接近多项式级时间内完成求解［15］。

目前，量子计算机正处于含噪声中等规模量子（noisy intermediate-scale quantum，NISQ）时代，由于量子计算机存在的噪声及规模瓶颈，仅依赖量子计算机无法独立完成完整的优化过程［16］。因此，适配NISQ 计算机的量子-经典混合优化框架成为目前最有希望展示量子优势且具有实际意义的量子优化 框 架 方 案［17］。 其 中，基 于 变 分 量 子 算 法（variational quantum algorithm，VQA）［18］的 决 策 优化框架最具代表性。VQA 在MIP 问题求解中的典型应用为量子近似优化算法（quantum approximate optimization algorithm，QAOA）［19］，QAOA 支 持 在NISQ 计算机下通过寻找哈密顿量的最小能量本征态以获得优化问题的近似最优解。基于此，本文将从可行性分析、建模方法、求解过程和技术展望4 个维度探析量子计算技术在新型电力系统的应用与发展，为相关优化问题的高效、精准求解提供一种新的思路。

1 量子计算赋能新型电力系统的可行性

1.1 量子计算技术基本原理

经典计算机使用经典比特作为计算的基本单元，每个比特可以表示0 或1；经典计算机通过逻辑门电路对一系列经典比特进行加工，实现各种数值或逻辑运算。经典优化算法是由编程语言形成一套计算逻辑，当其在经典计算机上运行时，需要借助编译器将算法翻译成机器语言，再由计算机硬件进行处理和运算。经典计算机以串行的方式对比特流进行处理，即使经典计算机在不断地发展与提升，其计算性能仍存在上限。

不同于经典计算机，量子计算机的最小计算单元是量子比特，量子比特具有叠加的属性，可以同时处于0 和1 的叠加态，具有强大的并行计算能力。加之量子纠缠、相干等特征，量子计算机在某些情况下能够执行经典计算机无法完成的任务。量子优化算法运行在量子计算机上，是一种遵循量子力学规律操控量子比特进行运算的方法。在VQA 框架下，量子优化算法求解问题的核心在于设计一套与优化问题匹配的外部作用机制（如量子门电路或横向磁场），当代表0-1 整数变量的量子比特经过外部作用后，可朝着最优解的方向演化，并在被观测时以较高的概率坍缩至最优解对应的量子态，从而实现算法的寻优。量子计算与经典计算在实现过程中的差异如附录A 图A1 所示。

1.2 量子计算的先进性及优势

随着新型电力系统的持续建设，并网机组多、求解对象复杂、求解算法效率偏低与算力配置紧缺的矛盾日益突出。新型电力系统在规划［20-23］、运行［24-26］以及市场决策［27-28］过程中，存在无法在规定时间内收敛至误差精度范围内的可行解［29］的瓶颈。作为一种新兴的计算范式，量子计算的技术优势与新型电力系统MIP 问题的求解难点高度契合；同时，相比于经典计算，量子计算在效率上具有显著的优越性，如图1 所示。因此，将量子计算技术应用于新型电力系统决策优化，具有一定的理论基础和实际价值。

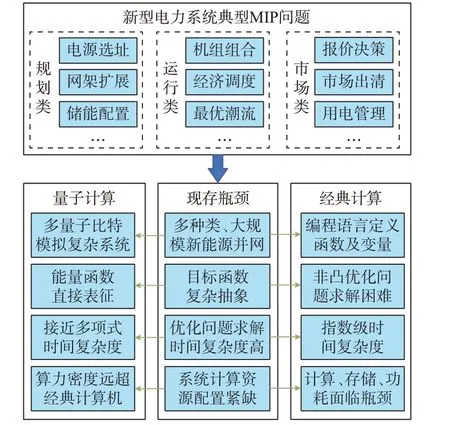
图1 量子计算的适配性及优势Fig.1 Adaptation and advantages of quantum computing

1）由多个量子比特构成的量子系统具备描述大规模的新型电力系统的能力。在新型电力系统的优化问题中，量子比特可作为决策变量的表征参与运算，任意类型的变量均可映射至量子计算机中的一个或多个量子比特。

2）优化问题的目标函数可用量子系统的能量函数表征。能量函数和目标函数的变化趋势具有一致性，当系统的能量状态处于最低点时，目标函数同步达到极值。

3）量子计算的速度优势可打破新型电力系统面临的计算效率瓶颈。随着电力系统规模的增大，经典优化算法的计算复杂度呈现指数级增长；而得益于量子比特具有的“状态叠加”属性，对于一个N量子比特的系统，对量子态的一次操作可等效为对2N个经典比特的同时计算［30］。因此，对于相同规模的问题，量子优化算法的计算复杂度远低于经典优化算法。

4）量子计算机能够大幅提升新型电力系统的算力水平。随着后摩尔定律时代的到来，采用冯诺依曼架构的经典计算机逐渐面临“计算墙”“存储墙”和“功耗墙”等问题［31］，而量子计算机利用量子的叠加、纠缠和相干属性实现并行求解，极大地提升了算力密度。

1.3 量子计算的局限性

目前，受限于量子计算软硬件技术的发展水平，量子计算技术在新型电力系统领域的应用仍存在以下限制。

1）单个量子比特变量只具备两种量子态，对于优化问题的连续变量，需要用多个量子比特进行描述，导致问题求解规模增大。而对于NISQ 时代的量子计算机，由于不可避免的噪声干扰，求解规模的增加意味着整个量子系统可靠性的降低［32］，一旦出现其中一个量子演化失败的情况，前期的迭代结果将全部作废，量子计算机将需要重新执行计算过程。在这种情况下，量子计算的优越性将无法凸显。

2）量子演化的执行需要具备相当苛刻的环境条件。目前的量子计算机需要在极低的温度下（接近绝对零度）运行［33］，同时，需要具备精密的隔离和控制条件。因此，量子计算的普及程度远远低于经典计算。另外，在量子演化过程中，为了避免量子从基态跃迁至激发态，其演化速率将受到严格的控制［34］，这也导致量子计算的速度优势无法充分体现。

1.4 量子计算技术的应用现状分析

为了充分发挥量子计算技术的适配优势，同时规避由于局限性带来的技术瓶颈，研究人员提出了VQA 决策优化框架以及多种与之适配的量子计算改进技术。其中，VQA 的内核是通过量子比特的演化寻找优化问题最优解，在量子计算机中利用参数化门电路使量子比特朝着特定目标进行演化，在经典计算机中对门电路参数进行调优，通过迭代使问题逐步逼近最优解。以VQA 作为基底的量子优化算法，是当前应用量子计算技术求解新型电力系统优化问题求解的主流方式。在VQA 框架下，优化问题的求解过程如图2 所示。

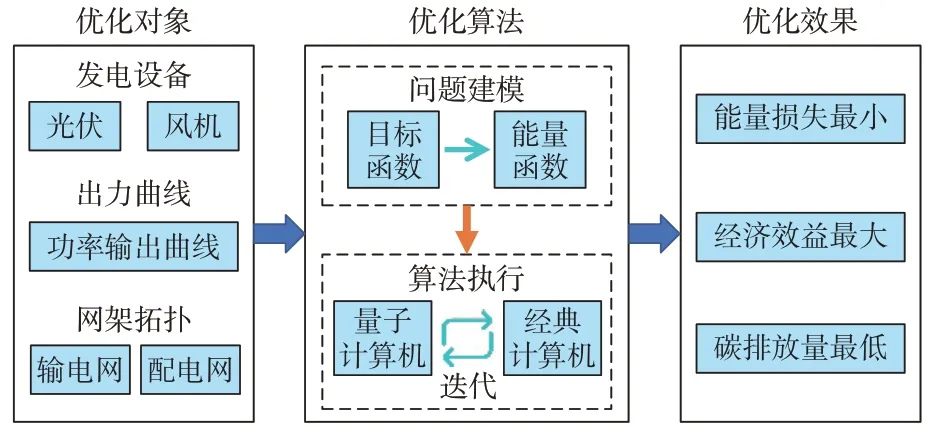
图2 VQA 框架下电力系统优化问题的求解过程Fig.2 Processes of solving optimization problems of power system in VQA framework

首先，根据实际问题的优化对象对优化问题进行建模，构造若干个量子比特组合成的量子系统；然后，在此基础上，将优化问题的目标函数替换为表征系统能量状态的能量函数，基于能量函数生成对应的量子电路，进而开始在量子计算机与经典计算机之间进行迭代优化；最后，基于问题求解的精度要求，结束迭代过程并输出能量函数对应的求解结果，实现对新型电力系统决策优化问题的求解。

与VQA 框架适配的量子计算改进技术主要包括将量子演化过程用参数化量子电路实现的量子电路编译（quantum circuit compilation，QCC）技术［35］，提升量子计算机测量精确度的量子误差缓解（quantum error mitigation，QEM）技术［36］和用于评估VQA 框架下各种量子优化算法性能的量子基准协议（quantum benchmarking protocol，QBP）［37］。

QCC 的原理类似于可编程逻辑电路，是将高级量子算法转化为底层量子电路的过程。它将抽象的量子算法转化为针对特定量子硬件平台的编译电路，通过使用分解、优化和映射的方法，使其能够有效和高度可靠地执行［38-39］。

QEM 旨在通过对有噪声测量结果执行事后处理实现对观测期望值的无误差估计，以减少量子计算中由噪声和错误引起的计算结果的偏差。它包括建立误差模型、测量校准、纠错编码、误差反馈控制和误差估计与补偿等多种技术手段。通过这些方法，量子误差缓解可以提高量子计算的精度和可靠性，克服噪声和错误对计算结果的影响。虽然QEM引入了因可观测方差增加而引起的额外采样开销，但同时也使系统对量子位和门电路层数的需求降低，所以更适合NISQ 设备［40-42］。

QBP 是一种用于评估和比较量子计算系统性能的标准化协议或方法［43］，不同基准评估方法可从低到高分被划分为3 个层级，分别为基础执行层级、量子门层级和量子电路层级［44］。较高层级的基准评估方法反映量子集成系统的性能，而较低层级的基准评估方法则用于评估量子计算机的可用性。QBP 规定了逻辑门集合、误差校准和纠正、测量和结果处理以及标准量子算法等方面的规范，以确保性能评估的客观性和可比性。

上述改进技术可用于表征和缓解误差，并实现具有一定抗噪能力的算法，从而实现对量子计算技术应用能力的探索和应用边界的开拓。

1.5 基于VQA 的求解基本框架

VQA 框架由能量函数、量子电路和参数调优3 个部分构成［45］。在此框架下，优化问题的目标函数被转化为向量θ的损失函数C(θ)，可由量子状态的观测结果得到。VQA 框架的核心在于构造一个多量子比特的系统，采用“量子-经典串行架构”，由量子计算机中的量子电路对初始量子态|s进行演化；同时，对演化后的量子态|ψ(θ) 进行测量，将观测结果传递至经典计算机，由经典计算机计算C(θ)，并完成收敛性判别和参数优化等步骤，最后判断是否执行下一次迭代。VQA 框架的介绍如附录A 图A2 所示。

VQA 框架在量子计算的基础上引入经典计算，实现了量子计算机高效演化与经典计算机灵活调参的结合，能够较好地规避当前量子计算技术面临的局限性。

1）在计算性能方面，VQA 已被证明具有天然的抗噪声能力，并且可较好地兼顾求解效率以及求解精度。同时，VQA 框架具有较强的扩展性，可通过量子计算机的分布式计算实现运算规模的提升。因此，VQA 被视作最有潜力在NISQ 计算机中展示应用级量子优势的算法框架［46］。

2）在量子演化方面，由于VQA 框架通过参数化量子电路对量子比特进行有指向性的模拟绝热演化，同时配置经典计算机对参数进行调优，可以显著缩短演化时间。

综上所述，VQA 框架既保留了与新型电力系统优化问题的适配性，又具备求解大规模问题的高效性和扩展性。因此，该框架是当前适合新型电力系统决策优化的有利框架。

2 量子框架下新型电力系统优化问题建模

2.1 新型电力系统优化问题的统一结构

新型电力系统规划、运行和市场等实际应用场景中存在求解对象规模较大的优化问题。为不失一般性，上述问题均可统一为MIP 问题（连续变量优化 问 题 可 视 为MIP 问 题 的 特 例）［47］。在MIP 问 题中，新型电力系统中的整数变量可用于表示诸如设备启停或是否接入等二值状态，为0-1 变量；其余为连续变量，可用于描述如功率、电价等因素。此外，新型电力系统MIP 问题大多为线性模型，或可基于分段线性化等技术表示为线性模型的形式。基于此，其统一的优化问题结构为:

式中:x与z分别为连续向量和0-1 变量组成的向量；A与B为常系数矩阵；a、b与c为常系数向量；K为0-1 变量的个数。

2.2 优化问题的伊辛模型

基于VQA 框架对优化问题式（1）进行求解的前提是构造反映其能量的伊辛模型，如附录A 图A3所示，量子计算机中量子比特的叠加态天然适用于表征整数变量，而量子比特绝热演化又与优化问题寻优相匹配［48］，故最优化问题的寻优过程被转化为通过量子绝热演化的方式寻找能量函数的最小值。

伊辛模型能量函数H（σ）的标准形式为:

式中:Jij为能量耦合系数，反映了量子i与j之间的耦合状态；N为量子比特数；hi为外部磁场对量子i的作用系数；σi为伊辛模型中量子i的自旋状态，取值规律如式（3）所示。

由式（2）和式（3）可知，伊辛模型的能量函数仅由量子间的相互作用和外部磁场对量子的作用两部分构成。因此，适用于量子计算机求解的最优化模型应满足以下条件:模型无约束条件，决策变量为整数变量且取值范围为{-1，1}，并且目标函数只允许出现单个决策变量或者相异的两个决策变量相乘两种形式。应用伊辛模型，可在多项式时间复杂度内精确求解大量运筹学领域含有整数变量的NP-hard问 题，如 旅 行 商 问 题［49］、背 包 问 题［50］和 最 大 割 问题［51］等。针对新型电力系统特定的MIP 问题，可将其转化为伊辛模型，并利用量子计算处理整数变量的独特优势快速精确求解。

2.3 伊辛模型构建方法

从新型电力系统优化问题的一般形式向适配量子计算伊辛模型的转化过程如附录A 图A4 所示。具体如下。

1）约束条件向目标函数转化

基于拉格朗日乘子法［52］或罚函数法［53］等，可将最优化问题的约束条件向目标函数转化，把有约束优化变为无约束优化。以拉格朗日乘子法为例，对最优化问题式（1）引入拉格朗日乘子λ后，可构造如式（4）所示的拉格朗日函数。

2）连续变量离散化

连续变量离散化是一种将连续变量转化为0-1变量的方法，如二进制展开、等间距离散化等。以二进制展开为例，对于x中任意一个非负连续变量xi，均可用a+b个0-1 变量zij的线性组合表示，如式（5）所示。

式中:a为log2xi向下取整值；2-b为展开的精度。

此外，由于式（4）引入了拉格朗日乘子λ，故需要仿照式（5）对λ进行离散化处理，形成如式（6）所示的无约束0-1 变量优化问题。

式中:A′与B′为常系数矩阵；a′为常系数向量；z∈{0，1}K，z1∈{0，1}K1，z2∈{0，1}K2，z1与z2分 别 为x与λ离散化后的0-1 变量组成的向量，K1与K2分别为x与λ中0-1 变 量的个数。

进一步，可将式（6）整理为如式（7）所示的标准型。

3）目标函数变形为伊辛模型能量函数

将式（7）中的各向量和矩阵展开后，所有0-1 变量可统一用z′i表示，如式（8）所示。

式中:A′ij与B′ij为常系数矩阵A′与B′中的元素；zi为z中第i个元素；a′i、bi与ci分别为常系数向量a′、b与c中的元素；Cij与di分别为二次项与一次项的系数。

进一步，将0-1 变量z′i转换为自旋状态σi，经严格 证 明［54］，z′i与σi之 间 满 足 如 式（9）所 示 的 对 应关系。

将式（9）代入式（8），可得到以σi表示的目标函数，如式（10）所示。

式 中:Jij和hij分 别 为σiσj项 与σi项 的 系 数；Cconst为 常数项。

由于常数项不影响优化问题的求解，故可将式（10）中常数项忽略。此时，原问题已从最优化问题式（1）转换为适配量子计算机的伊辛模型能量函数式（2）。将式（2）作为VQA 框架下的目标函数，其中，与σiσj相关的二次项可以被映射到量子比特之间的相互作用大小，与σi相关的一次项则表示量子比特自身的能量状态，通过调整VQA 中的变分参数不断优化量子态来最小化式（2），从而获得最优化问题式（1）的最优解。

3 基于QAOA 的新型电力系统决策优化技术

3.1 QAOA

VQA 框架下衍生出了多种量子-经典混合优化算 法［55-57］，其 中，最 具 代 表 性 的QAOA 由Farhi 等3 位 学 者 于2014 年 首 次 提 出［11］，已 有 学 者 针 对QAOA 在电力系统领域的应用展开了探索性研究。文献［58］阐述了QAOA 在求解电力系统优化问题时所具备的计算效率及准确度上的优势。文献［59］对QAOA 在智能电网领域应用的研究成果做了系统性的梳理与归纳，指出当前研究的热点聚焦在机组组合以及电网规划领域。在机组组合的研究中，文献［60］提出了一种结合QAOA 与拉格朗日松弛法的机组组合优化算法；文献［61］将机组组合问题抽象成一个二次无约束优化问题，并用QAOA 进行求解；文献［62］利用QAOA 解决了微电网场景下的机组组合问题。在电网规划领域，文献［63］提出了一种基于QAOA 的最优规划方法，用于解决在信息-物理系统下分布式电源的接入问题。

QAOA 从量子绝热演化理论［64］出发，利用参数量子门电路作用于输入的量子比特，以实现模拟量子绝热演化过程的目的。QAOA 结合了量子计算和经典计算的优势，量子计算机迭代进行量子态的制备、变换和测量，使量子比特快速演化至全局最优解对应的量子态；经典计算机则对量子门电路的参数逐步进行优化。在演化过程中，量子系统的哈密顿量H0如式（11）所示，只要演化时间T足够长，演化步长t足够小，系统的能量就能够从如式（12）所示初始哈密顿量HB的基态演化至如式（13）所示末态哈密顿量HC的基态，该过程可视为对能量函数的最小化。

每一次迭代时，QAOA 使用一个可变层数的量子电路来构建量子态，通过经典计算调整量子电路中旋转门的角度，以逐步逼近问题的最优解。量子计算机以离散化的p层量子门操作代替所述耗时的绝热演化过程；而量子门参数的优化与收敛条件的判断则由经典计算机执行。一方面，为了避免量子在演化过程中从基态跃迁至激发态，算法采用“近似绝热”的方式进行演化，即p值在满足量子电路设计要求的前提下尽可能大，但随之而来则是演化时间的增长；另一方面，对于优化问题而言，p值越大，目标函数越接近真实的最优解，但由于QAOA 的计算时间复杂度为O（n2p）［65］，过大的p值会直接导致计算效率的下降，故在实际应用中，p值的选取存在上限［66］。

QAOA 流程如图3 所示。QAOA 在连续迭代计算过程中，当量子比特输出状态的平均值趋于稳定时，可以认为量子部分完成“近似绝热”演化；当目标函数值或量子门电路参数变化小于容许误差时，可以认为经典部分收敛。量子计算机与经典计算机具体的执行过程如3.2 节和3.3 节所示。

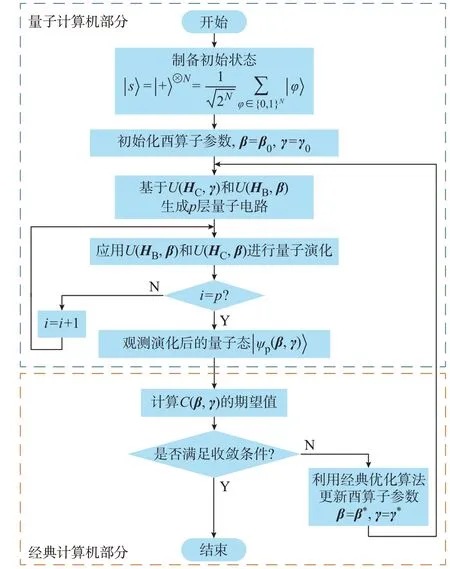
图3 QAOA 流程图Fig.3 Flow chart of QAOA

3.2 量子计算执行部分

通过量子门电路实现量子系统哈密顿量演化的过程如下。

1）制备初始态

在量子优化算法中，通常选取量子的均匀叠加态作为量子门电路的输入。可通过Hadamard 门矩阵H将|0 转化为均匀叠加态的量子比特|+ ，过程如式（14）所示。

式中:|0 和|1 为量子的2 个不同状态。

因此，对于N个量子位的门电路，输入|s可表示为N个均匀叠加态的张量积，即可用N维标准正交基线性表示，如式（15）所示。

2）酉变换操作

由薛定谔偏微分方程可知，量子态的演化可以表示为非时变哈密顿量HC对该量子系统的作用［67］。通过求解式（16）可得到量子系统在t时刻的状态。

式中:h 为约化普朗克常数。

为模仿式（16）所示量子绝热演化过程，使量子由初始状态演化至哈密顿量较低的末态，QAOA 引入了2 种酉算子U(HC，γ)和U(HB，β)，表达式为:

式中:β和γ为矩阵形式的酉算子的参数。

将p个U(HC，γ)和U(HB，β)分别作用于输入，具体由RZ门和RX门执行；最终得到演化后的量子态|ψp(β，γ) ，如式（18）所示。

3）输出测量

对演化后的量子态|ψp(β，γ) 进行多次观测，可得到损失函数C(β，γ)的期望值，如式（19）所示。当|ψp(β，γ) 的哈密顿量等于最小能量本征态时，C(β，γ)的期望值达到最小，即量子“近似绝热”演化结束。

3.3 经典计算执行部分

经典计算机收到量子计算机传递的观测结果后，完成能量函数的计算以及收敛性的判别，若满足收敛条件，则可认为算法已经找到一个误差允许范围内的近似最优解，QAOA 结束迭代；否则需要采用经典参数优化算法对参数β与γ进行调优，再将优化后的参数β*与γ*输入量子计算机进行下一次的量子态制备。典型的优化方法可以分为梯度下降法和非梯度法。其中，梯度下降法的原理如式（20）所示。

式中:k为优化步数；η为优化步长；∇为梯度求解算子。

通过求解C(β，γ)的梯度可准确得到β与γ优化的方向，以便迭代更新β与γ的取值。相关算法有批量梯度下降算法［68］、随机梯度下降算法［69］、自适应矩估计算法［70］、差分梯度下降算法［71］和基于梯度估计的同步扰动随机逼近算法等。然而，当量子门电路层数过多或伊辛模型过于复杂时，C（β，γ）的梯度求解将十分困难。一种解决思路是通过如式（21）所示的差分方法进行梯度计算。

式中:C*（β，γ）k为观测后的C（β，γ）值。

另一种思路则是采用非梯度法获得β与γ的一个足够优的改进方向，通过迭代更新最终趋近于最优的β与γ的取值，其相较差分梯度下降算法在计算精度上有着明显优势。相关算法包括下山单纯形算法[72]、方向加速法[73]、粒子群算法[74]、贝叶斯估计算法[75]、神经网络算法[76]等。

4 赋能新型电力系统的量子计算技术发展前沿与展望

4.1 硬件发展强化算力性能

量子计算机以及相关量子计算技术已经在理论中被证明其在求解新型电力系统特定的优化问题时具有一定的优越性，但要完全实现“量子霸权”［77］，即量子计算机在特定实施例中表现出超越所有经典计算机的计算能力，仍然存在诸多问题与挑战。例如，当前量子计算机中量子比特运算规模有限［78］，量子比特自身的不稳定性也阻碍了大规模量子计算机的设计与研发；在提升量子计算机运算规模的过程中，量子比特的拓扑连接方式愈加复杂，单个量子比特的失效或将引发整个量子计算机的连锁计算错误。另外，当前量子计算机的易用性较差，由于缺乏成熟的量子电路编译框架以及开发语言，量子计算机的操作对于非专业人士来说仍然是一项严峻挑战。

为突破上述瓶颈，如表1 所示，量子计算机供应商聚焦在提高量子比特的数量和质量，致力于研发新的量子比特类型并凭借先进的超导体、离子阱等技术提升其稳定性，以扩大实际量子计算机中量子比特的规模［79-84］。此外，容错量子计算电路与量子计算机也在同步发展［85］，旨在基于新型量子纠缠技术，设计新型量子电路拓扑、误差补偿编码方案以及量子容错门操作，以纠正或容忍量子比特错误，研发具备容错能力的通用量子计算机，实现大规模复杂任务的可靠量子计算。更为重要的是，为推动量子计算机的广泛应用，亟须简化量子编程工具和用户界面，降低使用门槛，包括开发量子编程语言、封装量子与经典编程语言的函数接口、设计图形化编程界面等。

4.2 框架升级巩固算法优势

立足于量子计算机硬件发展，量子计算软件架构的升级进一步提高了量子优化算法的计算规模和效率，使算法进一步适配新型电力系统的大规模优化问题的求解。在量子-经典混合优化框架的基础上，可进一步构建如图4 所示的“热启动+分布式”量子决策优化框架。

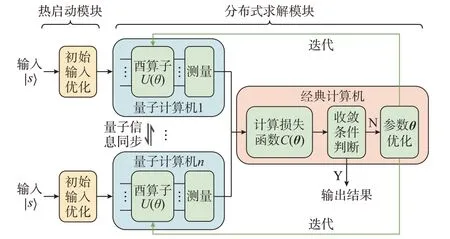
图4 “热启动+分布式”量子决策优化框架Fig.4 Warm-starting and distributed framework for quantum decision optimization

在VQA 决策优化框架中，对于任意的优化问题，初始输入均为多个量子比特的均匀叠加态|s；而前置了热启动模块后，可根据优化问题的特征对初始输入的量子比特进行优化［86］，从而有效缩短量子比特演化的过程，提高算法的计算效率。热启动模块的设计如下。首先，将优化问题的0-1 变量松弛为连续变量，利用经典计算机计算最优解；其次，将最优解通过特定的映射关系映射至0-1 变量的形式；最后，基于0-1 变量制备对应的量子比特作为优化后的初始输入。

分布式求解模块采用“多量子-单经典架构”，通过对量子比特或量子电路进行切割，实现将单个优化问题拆分至多个量子计算机进行分布式计算［87-88］，即由多个量子计算机同时进行量子态的演化，演化结果同时传递至同一个经典计算机，由经典计算机执行损失函数计算、判断收敛性以及参数调优的任务。相比于VQA 决策优化框架，量子分布式决策优化框架带来了计算规模上的提升，使其能够求解一些VQA 无法求解的大规模优化问题。但为了保证优化问题的全局最优，该框架需要协调各个量子计算机共同寻优，故需要耗费额外的量子比特用于量子计算机之间的信息同步。例如，求解一个含有m个0-1 变量的优化问题，需要制备m+ρ个量子比特，其中的ρ个量子比特用于多个量子计算机之间的通信。投入更多的量子比特和量子计算机开展分布式计算会产生更高的计算成本，损失了一定的经济性。

4.3 技术优化支撑计算精度

在改进框架特性提升算法性能的基础上，针对量子计算精度提升的研究也取得了长足的进展，主要包括噪声消减、模型降维和结果纠错三大方向。

在噪声消减的相关研究中，研究人员通过结合有约束的量子蒙特卡洛法和量子优化算法，构造出一种具有可扩展和抗噪声特性的量子-经典混合算法，该算法的计算性能与精度已经在16 量子比特的NISQ 计算机中得到验证［89］。在模型降维的研究中，通过构建基于非正交量子态的量子优化框架，将离散经典变量映射至处于非正交量子态的量子系统，可有效减少变分量子优化算法在计算中所需的量子位数量［90］。在量子纠错领域，利用微波简谐振子或玻色模式系统中的无穷维希尔伯特空间，可实现量子计算机的冗余编码与量子纠错［91］。此外，应用表面码纠错技术，可通过增加量子比特数量的方式实现量子错误率的降低［92］，将该技术应用于容错量子计算机的研发，有望实现与高准确率的容错量子计算。上述研究成果将使量子计算技术在大规模问题的求解中仍然保持较好的性能表现，为量子计算技术在新型电力系统决策优化的应用提供了强有力的技术支撑。

4.4 行业规划加速技术革新

从行业角度对量子计算的发展进行审视，受限于量子计算技术较高的研究门槛，当前无论是电力企业、高校或科研院所，在科研人力、理论技术积累、硬件与平台资源以及研发资金等方面均存在不同程度的缺口与瓶颈。为了促进量子计算技术在能源电力行业的快速发展和广泛应用，需要从科研模式创新以及人才培养机制上实现量子与电力行业的协同发展。

对于科研模式创新，需要形成产学研合作的科研创新模式，让电力企业、高校或科研院所深度协同合作，充分发挥自身优势，实现从资金到人才，从理论基础到软硬件平台的全方位资源共享，降低量子计算从科研到成果落地过程中消耗的资金及资源成本。在产学研结合模式的大框架下，可进一步实施产学研三方组织合作、高校自主产业化合作以及科研院所自主产业化合作等运作模式，通过资源整合填补现有针对量子计算行业发展及跨学科协作的空白，促进量子计算技术在能源电力行业的深度应用。

对于人才培养机制，可在产学研结合新模式的基础上，依托电力行业实践性强、项目资源丰富的优势，形成适用于量子计算行业人才培养的创新模式，打造理论与实践结合，多学科交叉的复合型人才培养体系；在此基础上，实施人才与项目深度绑定的策略，不但直接降低了人才培养成本，也能够使所培养的人才创造更大的经济价值，解决了科技人才培养机制单一、人才素质模型不均衡的问题。

5 结语

为应对新型电力系统在决策优化过程中面临的计算瓶颈，本文首先对量子计算技术的特性进行了剖析，说明量子计算技术赋能新型电力系统的必要性及可行性。其次，分别考虑量子计算机和经典计算机的优势，对面向新型电力系统优化问题的决策优化框架进行了设计。在此基础上，对新型电力系统优化问题的建模方式进行了总结归纳，将优化问题统一表征为伊辛模型的能量函数形式；并对量子优化算法应用于新型电力系统优化问题的过程进行了初步探索，为新型电力系统决策技术的发展开辟了新方向。最后，对量子计算前沿技术赋能新型电力系统的潜在方式进行了思考与展望。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。