“两尘四气”空气污染数据的校准模型

朱莹 姜道旭 盛俊 李建龙

摘 要：通过Excel软件对监测点收集的空气质量数据进行拆分及构造函数的方法，拟合了“两尘四气”的六个方程，这些方程可用于对自建点数据进行校准。在对所收集的数据标准化后，利用SPSS软件对“两尘四气”数据误差产生的原因进行回归分析，建立了多元线性回归方程。方程显示：压强、温度和风速更容易导致自建点数据误差，可使用对上述三种因素不敏感的材质制造检测仪的传感器。以上使用Excel和SPSS软件对大数据进行比对处理及建模的方法可用于环境监测、农业生产等领域促进高质量生态文明建设。

关键词：“两尘四气”；Excel和SPSS；曲線拟合；多元线性回归

中图分类号：X51文献标志码：A文章编号：1673-9655（2024）01-00-06

0 引言

随着国家对生态文明建设的大力推进，对以PM2.5、PM10、CO、NO2、SO2、O3为代表的“两尘四气”等空气污染进行实时监测，可以帮助管理部门对不同的污染源采取相应改善措施。对空气质量的监测分为国家监测控制站点（国控点）与民间自建监测点（自建点）。前者的优点是数据准确，缺点是布控点少，时间间隔大并滞后，监测仪价格昂贵；后者可对某一地区空气质量进行实时网格化监控，并能同时监测温度、湿度、风速、气压、降水等气象参数。国外已有一些学者分别关注于空气质量[1-4]、PM2.5、PM10[5-7] 、废气[8-9]，

国内也有学者的研究涉及了空气质量和数据监测，方法包括模糊-灰色聚类、分形模型等 [10-14]；另有一些学者关注了空气质量校准和优化[15-16]，

研究虽有新意但并不太全面。本研究以2019年全国大学生数学建模竞赛D题[17]为例，利用常规软件Excel和SPSS[18-19]，研究方法实现了用精确的国控点整点数据对近邻自建点数据的比对校准，对导致自建点与国控点监测数据差异的因素进行了分析。因有些气态污染物及天气会对自建点检测仪的传感器产生干扰，影响数据的质量，所以在同一时间自建点数据会与相应国控点的数据存在差异，本研究既可提高自建点空气质量检测仪的传感器精准度，又可以利用国控点数据对邻近自建点数据进行校准。

1 材料与方法

1.1 国控点数据对其近邻自建点数据校准建模

民间自主研发用于监测“两尘四气”数据的微型空气质量检测仪，其优点是监测实时且成本低，但核心部件电化学气体传感器长时间使用后会产生误差，且天气因素对传感器也存在影响。在国控点附近自建点的微型检测仪同一时间所采集的数据，与国控点的数据会存在一定的差异，因此将自建点数据通过适当数学模型进行转化与校准。本研究实现了对二十多万条的自建点大数据进行时间拆分和筛选，并根据赛题具体要求，构造了相关函数抓取整点前后5 min内所有数据，并取其均值。然后将处理所得数据与赛题所提供的国控点整点数据一一对应，分别对PM2.5、PM10、CO、NO2、SO2、O3用Excel建立数学模型的方法对自建点数据校准，并分别给出了拟合度R2。

图1～图6分别是PM2.5、PM10、CO、NO2、SO2、O3 自建点和对应国控点数据散点图与拟合曲线，表1列出了上述6种物质自建点浓度（解释变量x）与对应国控点数据（被解释变量y）拟合的方程，以及每个方程的拟合度R2。其中PM2.5、PM10和O3的拟合度较高，这三种物质自建点的浓度可以通过拟合曲线的方程进行转化；NO2、CO、SO2的拟合度较低，尤其是SO2浓度数据误差很大；因为SO2会溶于水中，形成亚硫酸；若加上PM2.5作用，便会迅速生成硫酸（这也是酸雨的主要成分）[20]，使得自建点传感器受到强污染导致数据失真有关。

国控点附近自建点的微型检测仪同一时间所采集的数据，与国控点的数据会存在一些差异，这些自控点数据可以通过上述表1模型进行转化与校准，进而转化为与国控点数据误差更小的数据，以弥补国控点的布控不足，以上拟合度较高的是PM2.5和 PM10。

1.2 自建点数据与国控点数据差异成因分析

自建点使用的微型空气质量检测仪的传感器是电化学气体传感器，温度、湿度、风速、气压、降水等天气因素对传感器会带来一定的影响。这些因素对传感器读取空气中的“两尘四气”数据的真实影响有多大，可运用多元线性回归方程模型，对自建点和国控点数据误差进行探究性分析。“两尘四气”里PM2.5、PM10、NO2、SO2、O3浓度单位是μg/m3，CO浓度单位是mg/m3、

温度单位℃、湿度单位rh%、风速单位m/s、气压单位Pa、降水量单位mm/m2，这些数据单位各不相同，因此先用公式Xi=（Xi-Xmin）/（Xmax-Xmin）对这些数据进行无量纲标准化处理，再用SPSS软件进行多元线性回归分析。

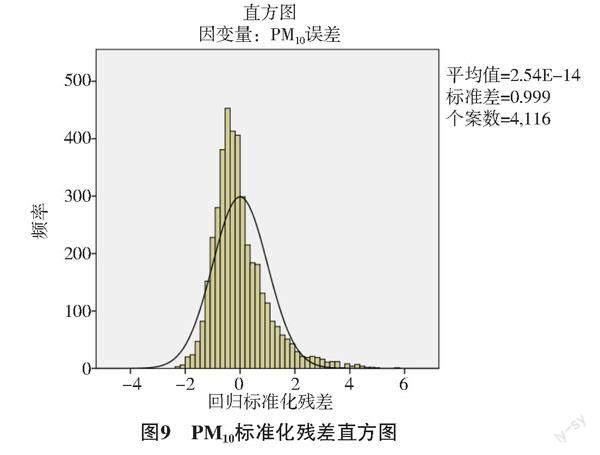
1.2.1 六种污染物误差多元回归模型的标准化残差直方图和P-P图

图7、图9、图11、图13、图15、图17分别是PM2.5、PM10、CO、NO2、SO2、O3数据误差的标准化残差正态曲线直方图。图8、图10、图12、图14、图16、图18分别是PM2.5、PM10、CO、NO2、SO2、O3标准化残差的正态P-P图，图中点基本在直线附近或在直线上，说明变量之间呈现线性分布。

1.2.2 “两尘四气”数据误差的多元回归模型与分析

为简化方程，误差值、温度、湿度、风速、气压、降水量分别用E、T、H、W、Pa和P表示。由多元回归方程可知，湿度、压强对PM2.5数据的误差产生较大影响；湿度、压强、温度和风速对PM10数据的误差影响较大；CO数据的误差大多由温度、压强和风速产生；温度、压强、湿度、风速和降水量都对NO2数据产生影响；SO2由于数据失真，所以拟合度不高，压强、温度对数据有一些影响；温度、压强和风速对O3数据影响较大。综合来看压强、温度和风速对数据读取产生的误差影响较大，空气质量检测仪的传感器可以考虑选用对压强、温度和风速变化不敏感的材质来制造，或经常更换新传感器以减少数据误差。

2 结论

本研究契合美丽中国对生态的要求，环境美、生态优的高质量生态文明建设是全体国人的追求。本研究使用了常规软件Excel和SPSS，数据拆分、构造函数、筛选、分类汇总、数据的标准化、公式等主要用于数据处理和曲线拟合；SPSS主要用于多元线性回归，并根据所得回归方程找出产生误差的原因，以便将来使用抗干扰能力更强的传感器获取数据。针对国控点数据的缺失，为了减少其对建立数学模型的不利影响，可以使用缺失数据临近时间的均值替代，或将自建点里面相关的数据剔除，这样可以保证自建点和国控点数据的一一匹配。

3 展望

徹底消除“两尘四气”对环境的污染目前还很难实现，但人们依然可以有所作为。比如：为了降低PM2.5，可以减少使用化石燃料并禁止燃烧垃圾；多浇水可以控制扬尘并降低PM10颗粒；不使用煤炉，少用燃油车可以降低CO浓度；城市集中供热可以减少锅炉使用降低NO2；使用优质煤可以减少SO2污染；无纸化办公可以减少复印机的使用，控制O3的污染等。

参考文献：

[1] L.V.Klochkova，Yu.A.Poveshchenko，V.F.Tishkin.Mathematical modeling of air quality on the prolonged period of time[J].ZhurnalSrednevolzhskogoMatematicheskogoObshchestva，2012（14）：2，67-73.

[2] Shakoor A，Chen X，Farooq T H，et al.Fluctuations in environmental pollutants and air quality during the lockdown in the USA and China：two sides of COVID-19 pandemic[J].Air Quality Atmosphere & Health，2020（13）：1335-1342.

[3] Zou Z，Zhao J，Zhang C，et al.Effects of cleaner ship fuels on air quality and implications for future policy：A case study of Chongming Ecological Island in China[J].Journal of Cleaner Production，2020（267）：122088.

[4] Sheng G，Dai J，Pan H.Influence of Air Quality on Pro-environmental Behavior of Chinese Residents：From the Perspective of Spatial Distance[J].Frontiers in Psychology，2020（11）：566046.

[5] Li Xiao long，Fang Zongyi.Comparison between Two Dust Weather Process EffectingBeijing in 2006 [J].Climate and Environmental Studies，2007，12（3）：320-328.

[6] Girolamo P D.Assessment of the potential role of PM2.5/PM10particles in intensifying the pandemic spread of SARS-CoV-2/COVID-19 in Northern Italy[J].Bulletin of Atmospheric Science and Technology，2020（1）：515–550.

[7] Hatta M，Han H.Predicting indoor PM2.5/PM10 concentrations using simplified neural network models[J].Journal of Mechanical Science and Technology，2021，35（7）：3249-3257.

[8] Liu X，Liu J，Chen J，et al.Study on treatment of printing and dyeing waste gas in the atmosphere with Ce-Mn/GF catalyst[J].Arabian Journal of Geosciences，2021，14（8）：1-6.

[9] Koci K，Reli M，TroppovaI，et al.Degradation of Styrene from Waste Gas Stream by Advanced Oxidation Processes[J].Clean， 2019，47（8）：1900126.1-1900126.9.

[10] 徐琴，王赪，汪宵，等.由光化学反应和排放清单判断城市PM2.5首要污染源的方法[J].扬州大学学报（自然科学报），2018，21（1）：68-72.

[11] 丁卉，刘永红，曹生现.基于模糊-灰色聚类方法的城市空气质量评价研究[J].环境科学与技术，2013（S2）：374-379.

[12] 陈辉，厉青，杨一鹏.基于分形模型的城市空气质量评价方法研究[J].中国环境科学，2012（5）：954-960.

[13] 徐戈，李宜威.空气质量对公众感知风险与应对意愿的影响研究[J].系统工程理论与实践，2020，40（1）：93-102 .

[14] 汪发元，郑军，汪宗顺.城市化水平、工业化水平对空气质量的影响分析—基于湖北省16 城市2005—2017年数据的时空模型[J].长江流域资源与环境，2019，28（6）：1411-1421.

[15] 雷耀建，王汝凉.最小二乘法在空气质量数据优化中的应用[J].南宁师范大学学报（自然科学版），2020，27（1）：51-56.

[16] 纪张伟.空气质量数据的校准研究[J].太原师范学院学报（自然科学版），2020，19（3）：44-48.

[17] 2019年高教社杯全国大学生数学建模竞赛赛题[EB/ON].（2019-09-12）[2020-01-08].http：//www.mcm.edu.cn/html_cn/node/b0ae8510b9ec0cc0deb2266d2de19ecb.html. 2019 Higher Education Association Cup National College Students Mathematical Contest in Modeling[EB/ON].（2019-09-12）[2020-01-08].

[18] EXCEL在基层统计工作中的应用[M].北京：中国统计出版社，2013：88-98.

[19] SPSS 21统计分析与应用从入门到精通[M].北京：清华大学出版社，2015：163-176.

[20] 韩军彩，陈静，王晓敏等.基于微波辐射计资料的石家庄市一次重污染成因分析[C]//北京：中国气象学会年会，2016：1-10.

Calibration Model of Air Pollution Data "Two Dusts and Four Gases"

ZHU Ying， JIANG Dao-xu， SHENG Jun， LI Jian-long

（Yangzhou Polytechnic College， Yangzhou Jiangsu 225009， China）

Abstract： In this paper， by using Excel software to split and construct air quality data，six equations of "two dust and four gas" were fitted to calibrate the data of self-built points. After data standardization， multiple regression of SPSS software was used to conduct regression analysis on the causes of data errors of "two dusts and four gas"， and a multiple linear regression equation was established. The equation showed that the pressure，temperature and wind speed have great influence on the error， and the sensor can be made with materials insensitive to the above three factors. The above data processing and modeling methods using Excel and SPSS software can be used in fields such as atmospheric environmental protection and agricultural production to promote high-quality ecological progress.

Key words： "two dusts and four gas"; Excel and SPSS; curve fitting; multiple linear regression

收稿日期：2022-10-31

基金项目：江苏省种植养殖业安全环境技术及装备工程研究中心开放课题（JSZY-2022-07）；揚州市职业大学2020年校级教改课题“以问题解决为导向的数学微课资源研发与应用”（2020JG33）。

作者简介：朱莹（1973-），男，在读博士生，副教授，江苏扬州人，主要从事数学建模等方面研究。