基于博弈论赋权信息量模型的滑坡易发性评价
2024-03-26崔成涛李丽敏符振涛任瑞斌王莲霞封青青
崔成涛 李丽敏 符振涛 任瑞斌 王莲霞 封青青

摘要:针对利用信息量模型进行滑坡易发性区划时,直接将各影响因子的信息量相加或乘以单一权重相加,未同时考虑因子的主、客观权重的问题,提出基于博弈论赋权信息量模型的滑坡易发性评价方法。首先采用层次分析法(AHP)计算出主观权重,通过变异系数法确定客观权重,然后利用博弈论原理进行主、客观权重的优化组合,得到组合权重;基于组合权重对各评价因子的信息量图层进行加权求和,通过自然间断点法将评价结果分为5类。最后以陕西山阳县为研究区,分别从滑坡易发性区划图、分区点密度及ROC曲线,将所提模型与单一权重的信息量模型进行了对比。结果表明,所提方法的准确性、可靠性优于传统的加权信息量法。
关键词:滑坡易发性;信息量;博弈论;变异系数法
中图分类号:P642.22文献标识码:A文章编号:1001-9235(2024)02-0009-09
Landslide Susceptibility Evaluation Based on Empowerment Information
Quantity Model of Game Theory
CUI Chengtao,LI Limin,FU Zhentao,REN Ruibin,WANG Lianxia,FENG Qingqing
(School of Electronics and Information,Xian Polytechnic University,Xian 710600,China)
Abstract:In the process of employing information quantity models for landslide susceptibility zoning,given that the information quantity of influencing factors is directly added or multiplied by a single weight,without considering the main and objective weight of the factor,this paper proposes an evaluation method based on the empowerment information quantity model of game theory.First,the analytic hierarchy process (AHP) is adopted to calculate the subjective weight,the objective weight is determined by the coefficient of variation method,and then the game theory principle is utilized to optimize the main and objective weight to get the combination weight.Meanwhile,the information layer of each evaluation factor is weighted and summed based on the combination weight,and the evaluation results are divided into five categories by the natural intermittent point method.Finally,by taking Shanyang County of Shaanxi Province as the research area,the proposed model is compared with the information quantity model of single weight in landslide-susceptibility zoning maps,zoning point density,and ROC curves respectively.The results show that the accuracy and reliability of the proposed method outperform traditional weighted information measurement methods.
Keywords:landslide susceptibility;information quantity;game theory;coefficient of variation method
根據自然资源部发布的全国地质灾害详细统计数据,2011年至2022年5月间全国累计发生地质灾害事件总数超过10万余起,共造成4 952人伤亡,其中仅滑坡灾害事件平均占比69.1%。因此,科学、准确的滑坡易发性评价显得尤为重要[1]。
常见的滑坡易发性评价模型主要有数据驱动和经验驱动模型2种,分别有:层次分析法[2]、频率比法[3]、证据权法[4]、逻辑回归[5]、神经网络[6]、模糊综合评判法[7]、信息量模型[8]、支持向量机模型等。在滑坡易发性区划中,研究区中的各诱发因子对滑坡发育的影响程度不同,因此很难从理论层面反映各滑坡诱发因子的不同分级对滑坡发育的影响,而信息量模型很好地解决了这一问题。其可以通过滑坡诱发因子所蕴含的信息量的大小,比较客观地反映滑坡诱发因子对滑坡发育的影响,因此在滑坡易发性评价领域应用广泛。张向营等[9]利用信息量模型对在建京张高铁沿线及邻区进行了滑坡灾害易发性评价,评价结果与实际灾害发生情况基本吻合,表明作为统计类的信息量模型在滑坡易发性区划领域具有很好的适用性,但其未考虑各评价因子间的权重关系,影响模型的评价精度。近年来,运用组合模型进行滑坡易发性评价已成为国内外学者的研究热点。孟晓捷等[10]将层次分析法与信息量模型相结合,对天水市麦积区幅进行滑坡易发性区划,取得了较好的结果。张志沛等[11]利用熵指数模型确定各评价因子的客观权重,提出加权信息量模型进行滑坡易发性区划。林荣福等[12]通过随机森林模型确定各评价因子的权重,结果表明所提方法的准确度高于传统的信息量模型。但以上模型进行滑坡易发性区划时均只考虑了单一权重,未充分的考虑各评价因子的主、客观权重对滑坡评价因子信息量造成的影响。
因此,本文提出基于博弈论加权信息量法,采用层次分析法(AHP)确定评价因子的主观权重,变异系数法计算评价因子的客观权重,利用博弈论原理优化主客观权重,。该法可以充分考虑评价因子之间的权重关系,将专家经验的主观性和滑坡数据的客观性相结合,提高了滑坡易发性评价的准确性。
1 研究区概况及研究方法
1.1 研究区概况
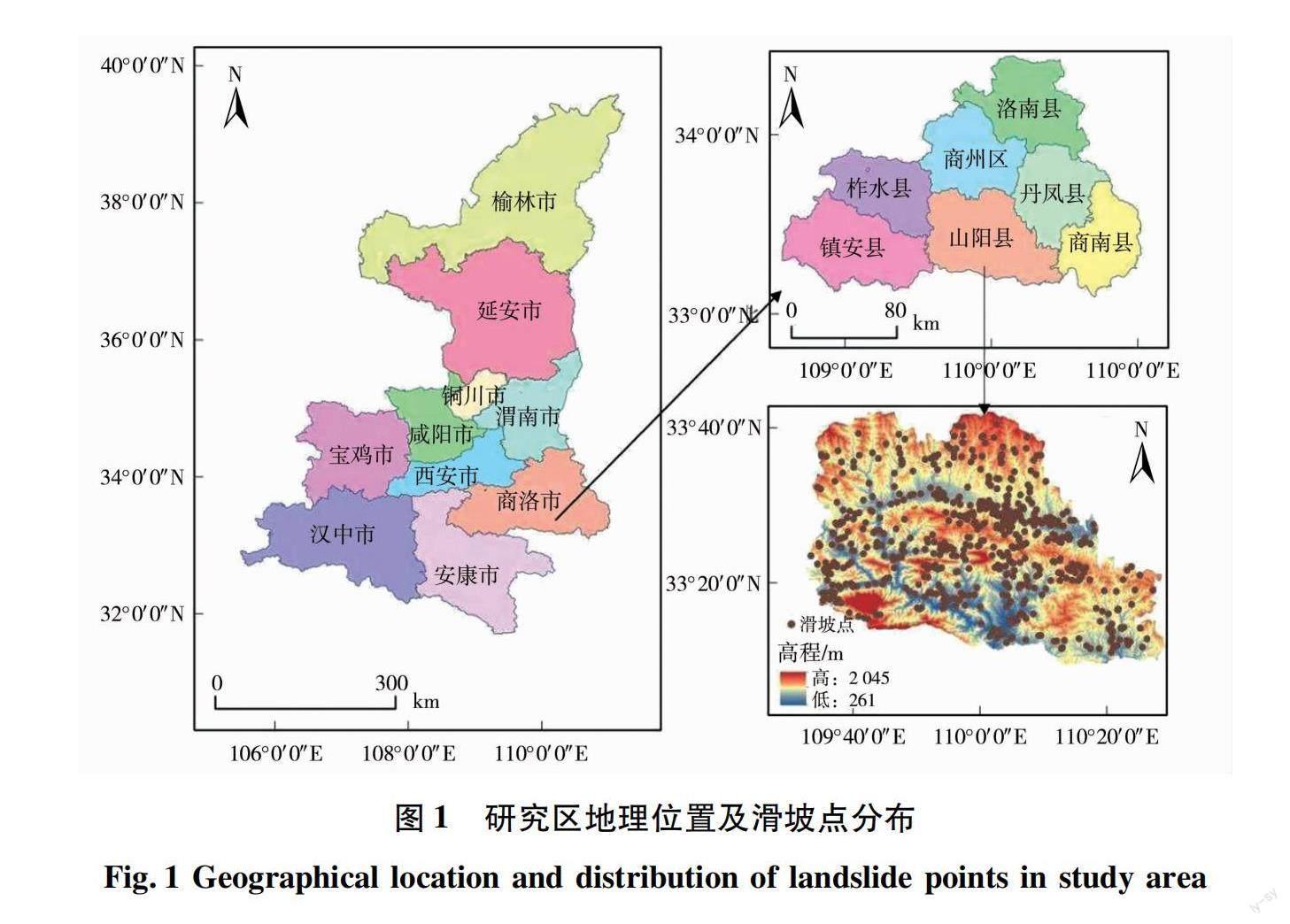
山阳县位于陕西省商洛市南部,北与商州市相连,南与湖北省郧西县接壤,西与镇安县、柞水县为邻,东靠丹凤县与商南县。地理位置为东经109°32′~110°29′,北纬33°9′~33°42′。总面积为3 529.18 km2,东西长约88.91 km,南北宽约62.02 km。境内最高海拔为2 045 m,最低海拔为261 m,平均海拔为1 120 m,境内北有流岭、中有鹃岭、南有郧岭,山大沟深,因此耕地与河流较少,多以丘陵、山地为主。境内主要水系有银花河、金钱河、谢家河等。山阳县境内有区域性大断裂2条,一般性断裂8条。境内人类工程活动主要以耕种坡地、修建房屋与道路为主,对地质环境的依赖程度高,同时对环境的影响和破坏也大,研究区地理位置以及滑坡点分布见图1。
1.2 研究方法
1.2.1 层次分析法(AHP)
层次分析法是可以反映指标间的重要程度的一种主观赋权法,具有权重确定合理、可参考历史经验的优点,在地质灾害领域应用广泛,比较适合既需定量又需定性的评价[13]。具体步骤如下。①构建判断矩阵。对于x1、x2、…xn个评价因子,通过专家进行两两对比得出判断矩阵X。②计算权重。设存在与矩阵X相同阶数的正向量M,使得XM=λmaxM,λmax为矩阵X的最大特征值,M为λmax的特征向量,对矩阵X进行求解,所得到的的解即为各评价因子对应的权重值。
1.2.2 变异系数法(CV)
变异系数法是一种客观赋权法。其思想在于利用数据的变异系数进行权重赋值,如果变异系数越大,说明其携带的信息越大,因而权重也会越大[14]。计算见式(1)、(2):
1.2.3 博弈论组合权重(GW)
主客观权值计算之后,根据博弈论[15]的思想进行组合权重的计算。
记Mi和Ni的组合权重为式(3):
W=aMi+bNi(3)
式中a、b为权重系数,a+b=1。
根据博弈论思想,使主客观权重之间的离差和最小,建立目标函数见式(4):
根据微分原理,要使目标函数取得最小值,需满足一阶导数为式(5):
计算出a和b,从而计算得到组合权重W。
1.2.4 信息量模型(I)
信息量(Information,I)模型是一种统计类模型,通过对滑坡历史数据进行统计分析,将各个滑坡诱发因子的实际值转换为蕴含滑坡信息大小的信息量值,其可以反映因子对滑坡发生的信息量大小,通过各个因子所含信息量值的总和反映滑坡的易发性[16]。单个因子信息量值计算见式(6):
Ii=ln(Qi/Q)/(Si/S) (6)
式中 Qi ——评价因子类别内的滑坡点个数;Q——滑坡点总数;Si——研究区评价因子类别的面积;S——研究区总面积。
评价单元总信息量值计算公式为式(7):
式中,I表示评价单元总信息值,反映了滑坡的易发性大小,判断其实数范围内的大小关系,值越大表示该单元的地质条件更易诱发滑坡。
1.3 数据来源
本文滑坡易发性评价的数据源主要包括:①山阳县自然资源局滑坡灾害信息数据;②山阳县1∶5万地质图,进行矢量化之后得到地层岩性和距断裂距离数据;③年降雨量、植被类型、土地利用数据来源于中国科学院资源环境科学与数据中心;④山阳县DEM数据来源地理空间数据云,像元大小为30 m×30 m,提取高程、坡度、坡向数据;⑤道路数据来源于Open Street Map。
2 评价因子选择与分析
2.1 评价因子的选取
不同研究区的滑坡影响因子均不相同,通过对山阳县历史滑坡信息进行调研,并考虑研究区的特征因子对育发滑坡的影响程度,最终选择地形地貌、人类活动、地质条件、水文因素等4大类因子,包括高程(A)、坡度(B)、坡向(C)、土地类型(D)、距断裂距离(E)、地层岩性(F)、距道路距离(G)、距水系距离(H)和年平均降雨量(I),总计9个指标因子,见图2。借助ArcMap软件,将山阳县划分为3 922 317个30 m×30 m的栅格。
利用ArcMap软件中的自然断点法进行项指标因子的分级。信息量值的大小反映了各指标因子的各个等级对发生滑坡的影响程度,信息量值越大,表明该因子等级区间对发生滑坡的重要程度越大,由式(6)计算各个因子分级信息量值见表2。
2.2 评价因子分析
2.2.1 地形地貌
本文通过提取分析山阳县DEM图得到高程、坡度、坡向因子。高程数据间接反映了滑坡体的坡势变化、植被类型、人类活动强烈程度以及地震等因素,是诱发滑坡的一个不可或缺的因子。将山阳县高程数据分为4个等级,见表2,可以看出,滑坡主要发生在<500 m、500~1 000 m范围,占总数的71%。原因是在该范围内,人类活动强烈,多进行房屋、道路建设,外加自然降雨因素的影响,易造成滑坡的发生。按等间距法将坡度划分为4个等级,滑坡点主要分布在15~35°区间,信息量达0.108,相比于高坡度区间而言,中坡段更易引发滑坡。坡向可以反映滑坡体受阳光、降雨等自然因素的影響程度,由表可以看出,在135~225°(南)区间内,信息量为0.226,表明坡体朝南面时更易受到阳光、降雨等因素的影响。
2.2.2 人类活动
强烈的人类活动影响着滑坡体原始的地形、地貌,破坏滑坡体的稳定状态,进而引发滑坡。将土地类型划分为6类,当土地类型为栽培植被和草丛时,灾害点占比达65.87%,更易发生滑坡,信息量值高达0.302。在进行道路建设时,滑坡体周边的地貌会被破坏,道路附近修建大量的工业区、住宅区,人类活动加剧,促进了滑坡发育。将道路距离划分为4类,其中有257个灾害点,即40.66%的滑坡发生在0~500 m区间内,信息量值高达0.629。
2.2.3 地质条件
地质条件包括岩组、断裂距离。作为滑坡内在因子的岩组是发生滑坡的物质基础,不同类型的岩组对滑坡体发育的促进不同,其直接决定着滑坡体的稳定程度和空间分布。将岩组划分为6类,当岩组类型为土体时,相比于其他岩组类型,信息量值高达0.808,更易发生滑坡;其中440个滑坡点,即69.84%,近七成的滑坡发生于薄层状较弱浅变质岩岩组。通过自然断点法将断裂距离划分为4类,在0~500 m范围内,信息量值为1.406,原因是距离断层近,滑坡体状态不稳定,易引发滑坡。
2.2.4 水文因素
水文因素选取距水系距离、年平均降雨量。距离水系较近时,河流不断冲刷、侵蚀滑坡体岩组,易形成滑坡。将距水系距离划分为4类,在0~500、500~1 200 m范围内,滑坡体边缘受到河流的冲刷、侵蚀更为严重,共有556个灾害点分布其中,占比高达88.25%。降雨影响着滑坡体岩组的摩擦系数,使岩组表面软化,是影响滑坡体稳定性的重要因素之一。将滑坡点年平均降雨量划分为4类,有46%的滑坡点分布在972.961~1 017.908 mm范围内。
3 评价结果及精度验证
3.1 易发性评价结果
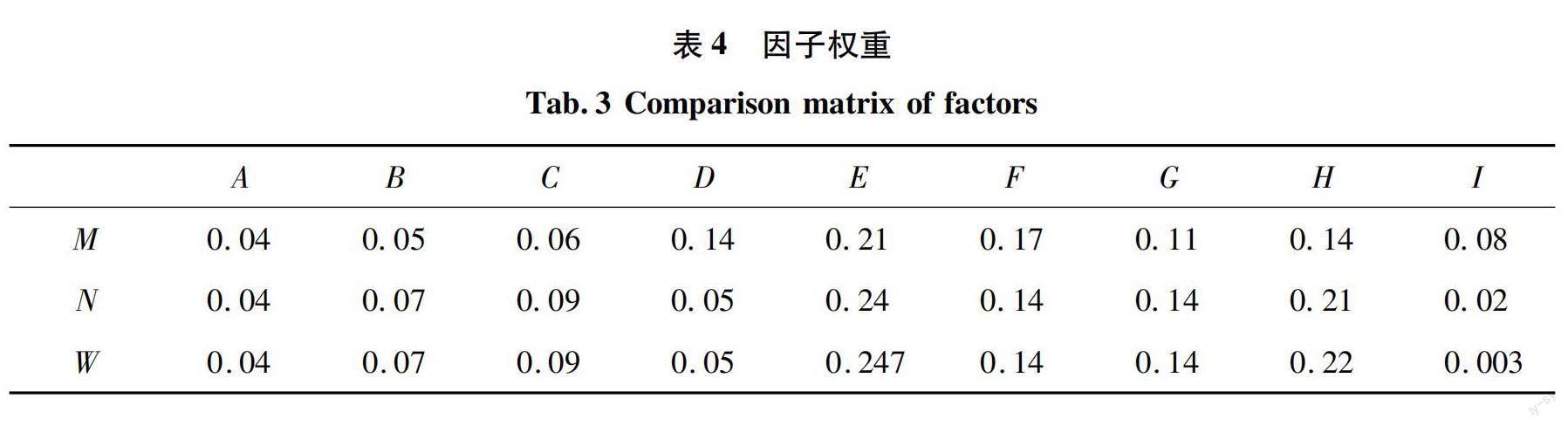
根据层次分析法,将滑坡诱发因子进行两两比对,得出因子判断矩阵见表3。将判断矩阵导入SPSS软件中得出最大特征值λmax为9.573,一致性指标CI为0.072,随机一致性指标RI为1.46,CR=CI/RI=0.049<0.1,一致性檢验通过,所计算的主观权重M(表4)可用于滑坡易发性区划。利用式(1)、(2)计算客观权重N见表4,通过式(4)—(6)计算组合权重W见表4。
将主观权重、客观权重和组合权重分别作为滑坡评价因子的权重,乘以评价因子信息量值后进行叠加,构成AHP-I模型、CV-I模型、GW-I模型,根据式(7),利用ArcMap中的栅格计算器,计算不同模型的信息量,进而得到整个研究区的信息量图层。利用自然断点法将不同模型的信息量划分为低易发、较低易发、中易发、较高易发和高易发5个等级,得到山阳县滑坡易发性区划见图3—5。
3.2 模型精度对比
对滑坡易发性分区图进行统计分析,结果见表5。3种模型评价结果具有一定的相似度,高易发区、较高易发区均呈东西分布,因为山阳县境内存在2条东西分布的区域性大断裂,处于断裂附近坡体稳定性较差,易诱发滑坡。其均主要分布在栽培植被、薄层状较弱浅变质岩岩组、地表落差较大等区域,区域面积分别为1 314.22、1 165.62、1 413.10 km2,低易发区主要分布在研究区西南方,该地区断裂较少、坡度较大,植被多为针叶林、岩组多为中厚层状坚硬碳酸盐岩岩组,地域条件不利于诱发滑坡灾害,分区面积分别为342.56、184.38、304.73 km2,滑坡点占比分别为0.95%、1.11%、0.63%,灾害发育程度较低。相比于AHP-I、CV-I而言,GW-I的易发性区划结果更加合理、准确。AHP-I、CV-I模型高易发区FR值分别为2.775、3.237,表明客观权重模型CV-I比主观权重模型在高易发区区划的评价精度更高。在低易发区的区划中FR值分别为0.098、0.213,表明主观权重模型AHP-I更适合于滑坡低易发区区划。而GW-I模型在低易发区的FR值为0.074,高易发区的FR值为2.584,所对应的高易发区面积为433.70 km2,相比于AHP-I、CV-I模型的345.28、360.02 km2有所提高,表明经过博弈论优化组合权重之后,结合了主客观权重的优点,定性与定量分析相结合,使得因子之间的权重分配更加合理,提高了滑坡易发性区划精度。
提取不同模型的测试集数据预测结果与其真实样本标签导入SPSS软件,进行受试者特征曲线(ROC)的分析与绘制,并进行ROC曲线与坐标轴所围面积(AUC值)的计算,见图6。
可以看出,AHP-I、CV-I模型的AUC值分别为0.809、0.822,而GW-I模型结合了AHP-I、CV-I模型的优点,AUC值为0.851,分别提升了0.042、0.029,可见GW-I模型比传统加权信息量模型更适合用于滑坡易发性评价。
4 结论
本文以陕西山阳县630组滑坡灾害点为数据点,选取高程、坡度、坡向、土地类型、距断裂距离、地层岩性、距道路距离、距水系距离和年平均降雨量,9个因子作为滑坡易发性区划的评价因子。采用AHP模型和CV模型确定评价因子的主、客观权重,通过博弈论原理优化组合权重,分别建立AHP-I、CV-I、GW-I模型对研究区进行滑坡易发性区划。结果显示:随着3种模型易发性等级的提高,相对应的灾害点密度也不断提高,相较于AHP-I模型,CV-I模型在高易发区的灾害点密度更大、低易发区的灾害点密度更低,模型的评价精度更高。GW-I模型结合了传统加权信息量模型采用主、客观权重分别加权的优点,在低易发区的灾害点占比分别降低了0.003、0.005,在较高易发区和高易发区的灾害点占比分别提高了0.062、0.079,AUC值分别提升了0.042、0.029。调研山阳县历史滑坡信息发现:滑坡灾害多发生于境内中部、东北部等地区,其中高坝店镇发生滑坡灾害最为严重,累计102起,占比0.41,其次为中村镇,总计47起,滑坡灾害情节较轻的为王闫乡,仅有8起。对比GW-I模型的滑坡易发性区划图,其在进行滑坡易发性区划时更加符合滑坡灾害点的实际分布情况,易发性区划精度更高。
参考文献:
[1]侯轶攀,杨宜军,王鹏来.小流域评价单元在地质灾害详细调查易发性分区中的应用[J].资源环境与工程,2019,33(s1):40-46.
[2]SAHA A,VILLURI VASANTA G K,ASHUTOSH B,et al.Development and Assessment of GIS-Based Landslide Susceptibility Mapping Models Using ANN,Fuzzy-AHP,and MCDA in Darjeeling Himalayas,West Bengal,India[J].Land,2022,11(10).DOI:10.3390/land11101711.
[3]FAN H D,LU Y F,HU Y L,et al.A Landslide Susceptibility Evaluation of Highway Disasters Based on the Frequency Ratio Coupling Model[J].Sustainability,2022,14(13).DOI:10.3390/land11101711.
[4]SADISUN I A,TELAUMBANUA J A,KARTIKO R D,et al.Weight of Evidence Method for Landslide Susceptibility Mapping in Sigi Biromaru,Central Sulawesi[J].IOP Conference Series:Earth and Environmental Science,2021,830.DOI:10.1088/1755-1315/830/1/012029.
[5]GANGA A,ELIA M,DAMBROSIO E,et al.Assessing Landslide Susceptibility by Coupling Spatial Data Analysis and Logistic Model[J].Sustainability,2022,14(14).DOI:10.3390/su14148426.
[6]薛正海 ,馮文凯 ,韩靖楠 ,等.基于信息量及层次分析关联法和BP神经网络耦合的滑坡易发性评价[J].桂林理工大学学报,2022,42(4):809-819.
[7]ZHAO H L,YAO L H,MEI G,et al.A Fuzzy Comprehensive Evaluation Method Based on AHP and Entropy for a Landslide Susceptibility Map[J].Entropy,2017,19(8).DOI:10.3390/e19080396.
[8]周天伦 ,曾超 ,范晨 ,等.基于快速聚类-信息量模型的汶川及周边两县滑坡易发性评价[J].中国地质灾害与防治学报,2021,32(5):137-150.
[9]张向营 ,张春山 ,孟华君,等.基于GIS和信息量模型的京张高铁滑坡易发性评价[J].地质力学学报,2018,24(1):96-105.
[10]孟晓捷 ,张新社 ,曾庆铭 ,等.基于加权信息量法的黄土滑坡易发性评价:以1∶5万天水市麦积幅为例[J].西北地质,2022,55(2):249-259.
[11]张志沛 ,魏在豪 .基于加权信息量模型的滑坡灾害易发性评价:以灞桥区为例[J].科学技术与工程,2020,20(9):3492-3500.
[12]林荣福 ,刘纪平 ,徐胜华,等.随机森林赋权信息量的滑坡易发性评价方法[J].测绘科学,2020,45(12):131-138.
[13]万松,范祝连,邓双,等.基于GIS的山地生态县域生态敏感性研究:以闽侯县为例[J].南方林业科学,2022,50(2):58-63.
[14]徐云飞 ,程琦 ,魏祥平,等.变异系数法结合优化神经网络的无人机冬小麦长势监测[J].农业工程学报,2021,37(20):71-80.
[15]王念秦,张帅,刘鹏.基于博弈论组合赋权法的泥石流灾害易发性评价云模型[J].长江科学院院报,2020,37(2):41-47.
[16]张钟远,邓明国,徐世光,等.镇康县滑坡易发性评价模型对比研究[J].岩石力学与工程学报,2022,41(1):157-171.
(责任编辑:程 茜)
