防振锤功率特性数值仿真与动力学优化

陈少宏，赵建坤，赵建利

（1.内蒙古电力（集团）有限责任公司，呼和浩特 010010；2.内蒙古电力（集团）有限责任公司内蒙古电力科学研究院分公司，呼和浩特 010020）

0 引言

运行在户外的架空输电线路会不可避免地受到自然环境因素的影响，特别是在稳定风激励的情况下，输电线路导线会产生不同形式的静、动态响应。输电线路风致动态响应是许多线路故障发生的主要诱因，会对输电线路的安全稳定运行产生不良影响[1-4]。当前，气候环境变化加剧，我国电网建设规模迅速扩大，线路风致灾害现象愈加严重，对线路安全稳定运行造成巨大威胁。线路风致故障形式主要包括微风振动、次档距振荡和舞动等，微风振动是危及线路安全运行最普遍的振动形式。

线路微风振动是一种由微风引起卡门涡街效应，进而使线路产生高频低幅振动的振动形式。振动频率区间主要集中在5～70 Hz，振幅较小，一般不超过10 mm。当风速达到一定值时，线路微风振动会引起线路共振，从而导致导线振动幅度急剧增加，易发生疲劳断线。在弯曲、负荷等力的作用下，导线振动频率会发生变化，进而影响线路微风振动的频率和振动幅度。微风振动是导致线路磨损、断股、断线以及金具损伤的主要原因[5-8]。为了减少线路微风振动带来的负面影响，目前工程上常用的方法是配置参数合理的防振锤，通过刚性固定的夹紧装置连接导线。当防振锤与导线的振动频率相同而发生谐振时，防振锤的质量-阻尼系统吸收部分导线振动能量，从而降低或消除导线风振带来的损伤，产生保护作用。目前，科研机构围绕防振锤数学模型构建、数值仿真、微风振动监测、防振方案设计等开展了大量研究[9-16]。

防振锤是目前我国使用最为广泛的输电导线防振装置，该装置主要通过吸收、减弱振动能量来减小输电导线在微风作用下所产生的振动幅度。防振锤一般根据经验来进行设计，其在不同工况下的防振性能有一定差别[17-19]，未能发挥出最佳防振性能。本文针对这一问题，对防振锤进行功率特性数值仿真计算，并在此基础上进行动力学优化，旨在提升防振锤的防振性能。

1 防振锤功率特性数值仿真

1.1 防振锤功率特性数据采集

对于安装在输电线路上的防振锤，其工作原理主要是利用风能驱动输电线路与阻尼器协同振动，通过将振动能量转化成热能或其他形式的能量进行消耗，达到降低导线振幅或消除风振的目的。为了分析防振锤在应用过程中的功率特性，提升其防振性能，需要调整防振锤的功率参数，并对该参数状态下的防振锤进行数值仿真。在仿真过程中，通过对防振锤施加激振力来获取功率特性数据。搭建实验装置，安装夹具、防振锤和传感器等，与计算机相连接，输入设定的振动参数，采集并记录加速度、激振力和相位角等数据，如图1所示。

图1 振动特性数据获取装置Fig.1 Device for obtaining vibration characteristic data

1.2 防振锤功率特性数值仿真

本文使用的防振锤型号为FR-3，对其进行功率特性数值仿真能够分析出防振锤的耗能特性，在此基础上进行动力学优化，能够提升防振锤的防振性能。防振锤的主要结构包括夹具、锤头和钢绞线，各部件之间的几何非线性较强。防振锤受激振发生振动时，钢绞线必然会发生弯曲和形变，在这个过程中，也能够消耗一定的风能。在数值仿真过程中，振动参数均是提前设置的。因此，振动过程中振动力所做的功可以通过计算得到；同时，钢绞线弯曲和形变过程中的能耗也能够计算求出。对于防振锤的功率特性，主要计算扭矩、剪力和弯矩的功率。假设防振锤的夹头采用刚性夹固方式进行固定（即夹头和同型轴的相对位置在运行时不会发生变化），而且在夹头两侧，夹头与同型轴之间的摩擦力也相对较小。因此，在计算防振锤的功率特性时，可以忽略夹头两侧，将夹头和同型轴作为一个固定的整体，并以夹固点为界将防振锤视为两个独立的子系统，该系统的简化模型如图2所示。

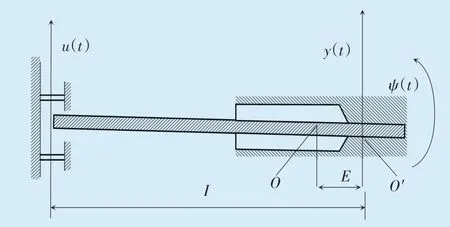
图2 防振锤子系统模型Fig.2 Subsystem model of vibration damper

图2 中，O表示锤头的质心，O′表示锤头与钢绞线的连接点，I表示锤头连接点与夹头夹固点之间的距离，E表示锤头连接点与锤头质心的距离，u（t）表示防振锤夹头在振动过程中所产生的位移，ψ（t）表示锤头的旋转角度，y（t）表示锤头与钢绞线连接点出口位置相对于夹头所产生的位移。该简化模型的动力学方程如下：

式中：M表示防振锤的质量矩阵；X表示垂直方向上的位移矩阵，Ẋ、Ẍ分别表示其一阶导数、二阶导数；F表示外荷载矩阵；K表示防振锤的刚度矩阵；C表示防振锤的阻尼矩阵，表达式如式（2）所示。

式中：D表示体系中的阻尼比；ω表示振动的圆频率。

当输电导线的振动比较稳定时，X可表示为：

实验测量出位移与振动的转动角度之后，即可求出防振锤的耗能：

式中：f0为绞线体系的支持力；v0为防振锤线夹振动速度；α为力和速度之间的相位差。

在实验装置上连接位移时程和加速度时程采集设备，得到防振锤在振动过程中的相关数据，代入式（4）中，忽略装置中其他微小部件对实验产生的影响，可得实验型号防振锤的功率特性曲线，如图3所示。

图3 防振锤功率特性曲线Fig.3 Power characteristic curve of vibration damper

从图3 可知，数值仿真结果与实验测定结果接近，说明防振锤的功率特性数值仿真结果具有可靠性。至此，完成了防振锤功率特性数值仿真计算。在实际应用中，还要在所得防振锤功率特性曲线的基础上进行动力学优化，提高防振锤的防振性能[20]。

2 防振锤的动力学优化

对于输电导线来说，横截面面积较大的导线在传输电能过程中自身消耗的电量较小。因此，我国电力工程往往使用横截面面积较大的输电导线，这种输电线在风荷载作用下产生的振动现象需要依靠防振锤来缓解。在大多数情况下，防振锤的减振功能函数与功率、频率等基本随机变量之间不存在显函数关系，因此本文采用Kriging模型对防振锤进行动力学优化。

Kriging模型属于一种无偏估计模型，这种模型的特点是实验过程中能够保证方差估计最小，能够较为准确地预测防振锤的防振性能[21-22]。在输入条件与输出值给定的情况下，相关模型参数需要进行有根据性的选取。

对于一组给定的样本点X=[x1，x2，…，xN]T和样本点响应值Y=[y1，y2，…，yN]（TN 为样本点数量），Kriging模型的数学形式可表示为：

式中：f(xi)为多项式函数，是该模型的确定部分；β为基函数系数；z(xi)为高斯随机函数。以防振性能最大化为目标，采用Kriging模型进行防振锤动力学优化时，选择一定数量的样本进行计算，可得对应目标变量的值。

在优化过程中，一旦建立了Kriging 模型，就认为该模型是一个全局高可靠性模型，不需要通过评估目标函数来更新代理模型。同时，这意味着优化值只取决于代理模型的精度。为了得到一个高精度的全局代理模型，需要大量的初始样本点，计算量大，而且全局收敛性无法保证，因此有必要在服从高斯分布的条件下，利用加权选择进行线性无偏估计，获取动力学优化的最佳路径。在动力学优化的过程中，为了避免局部优化，保证全局收敛性，首先要验证常用导线中最大振幅ymax与动弯应变ε之间的关系：

式中：d为导线直径；f为频率；m1为防振锤绞线单位长度的质量；J为绞线的抗弯刚度。在不同的档距、参数条件下，可以分析大截面导线微风振动的动弯应变值，确定优化的目标量。

其次，防振锤依靠其钢绞线的股间摩擦和材料内阻尼来消耗能量，从而抑制导线微风振动，保护线路安全运行[23-26]。对于本文选用的防振锤，其功率计算公式为：

式中：G为微风对防振锤的作用力；对于截面较为常见的导线，A为恒振动力系数。

至此，通过优化防振锤绞线的抗弯刚度、股间摩擦系数、材料内阻尼，完成防振锤的动力学优化。

3 模拟实验

3.1 实验装置与设备

为了验证防振锤功率特性数值仿真计算的有效性，在实验部分验证了防振锤的减振效果。本文的模拟实验在输电线路工程实验室中进行，搭建了大型反力架，模拟输电导线两端的固定方式。为了保证实验的准确性，在输电导线的实验段，利用线夹做一个间隔，使能量的传播与实际情况相近。在本文的实验装置中，档距设置为11.7 m，实验现场布置情况如图4所示。

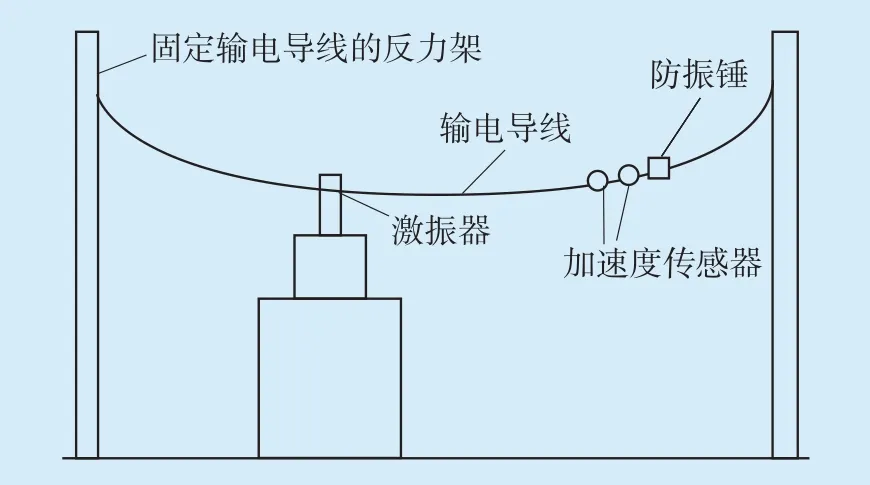
图4 实验室现场布置示意图Fig.4 Schematic diagram of laboratory site layout

实验选用的输电导线总长为14 m，单位长度质量为0.09324 kg/m，实验设备的相关参数见表1。

表1 设备参数Tab.1 Parameters of equipment

防振锤在输电线路中能够消耗的能量是体现其防振性能的重要参数。在实验中，本文选择了刚度较小的导线，因此，即使实验中设置的档距与相关标准的要求（档距为30 m）不相符，但是对实验结果的影响也不大[27]。

首先，将导线通过夹具固定在反力架中间，安装激振器、传感器和防振锤，对输电导线进行张力调节，使用激振器模拟微风对输电导线进行激振，激振器输出功率的计算公式为：

式中：Fj为激振器施加给输电导线的力；v 为激振速度；ϕ为激振器输出的力与加速度之间的相位差。记录激振实验过程的数据，完成一定频率下的防振锤耗能测试后，改变频率并重复上述过程。为了进一步验证实验结果的可靠性，根据输电导线的额定拉断力设定张力值，进行进一步计算。

3.2 动力学优化结果分析

为了从模拟实验的层面对实验方案的可行性以及装置设计的合理性进行验证，选择导线固有频率进行实验。不考虑输电导线的刚度时，固有频率的计算公式为：

式中：L为导线长度；T为张力；m2为导线单位长度的质量；n 为固有阶数。将输电导线的张力调整到额定拉断力的30%，即187.7 N，可得实验装置中输电导线固有频率的实验测定值，与理论值对比的情况如表2所示。

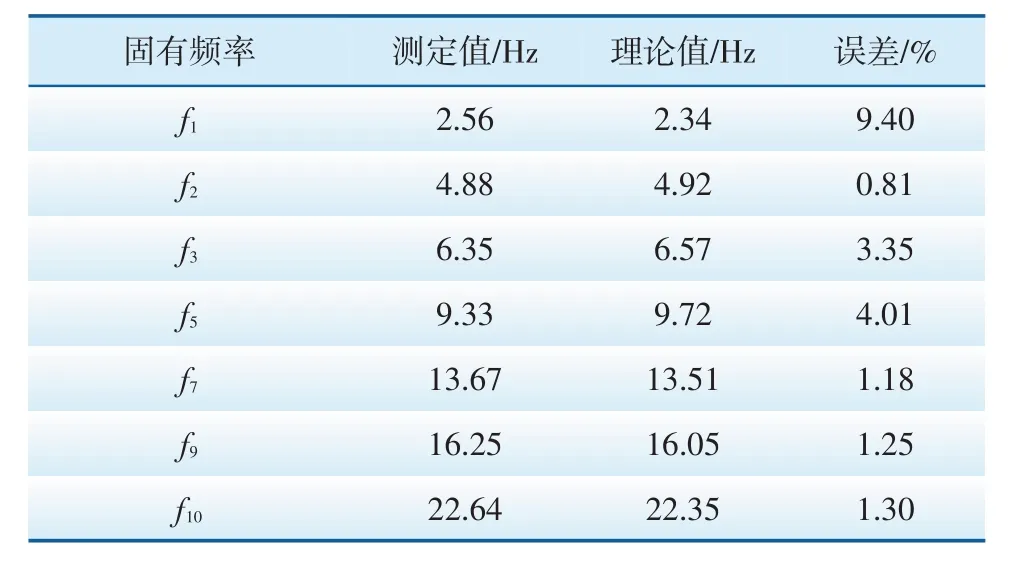
表2 导线固有频率的测定值与理论值Tab.2 Experimental and theoretical values of the natural frequency of the wire

由表2 可知，只有一阶固有频率的实验值和理论值间的误差超过5%，其余高阶固有频率的实验值与理论值较为吻合，实验装置的合理性得到了验证。随后，利用本文方法对防振锤进行动力学优化，得到优化后的防振锤绞线抗弯刚度、绞线股间摩擦系数、材料内阻尼，优化前后的动力学参数值如表3所示。根据表中优化后的动力学参数计算输电导线的振幅与比振幅值（ymax/d），并与优化前的情况进行对比，结果如表4所示。

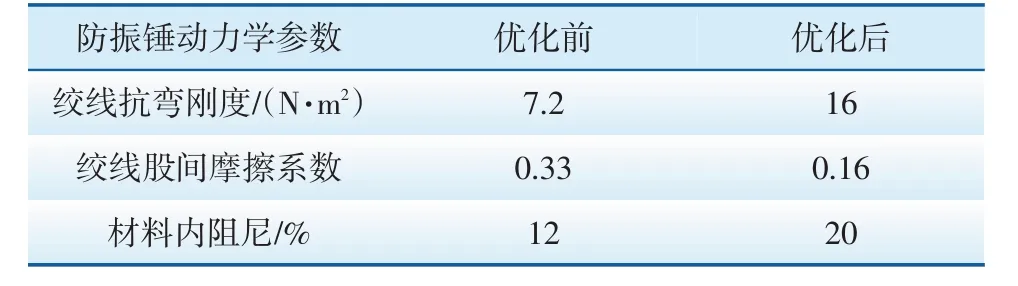
表3 防振锤动力学参数优化结果Tab.3 Optimized results of dynamic parameters of vibration damper

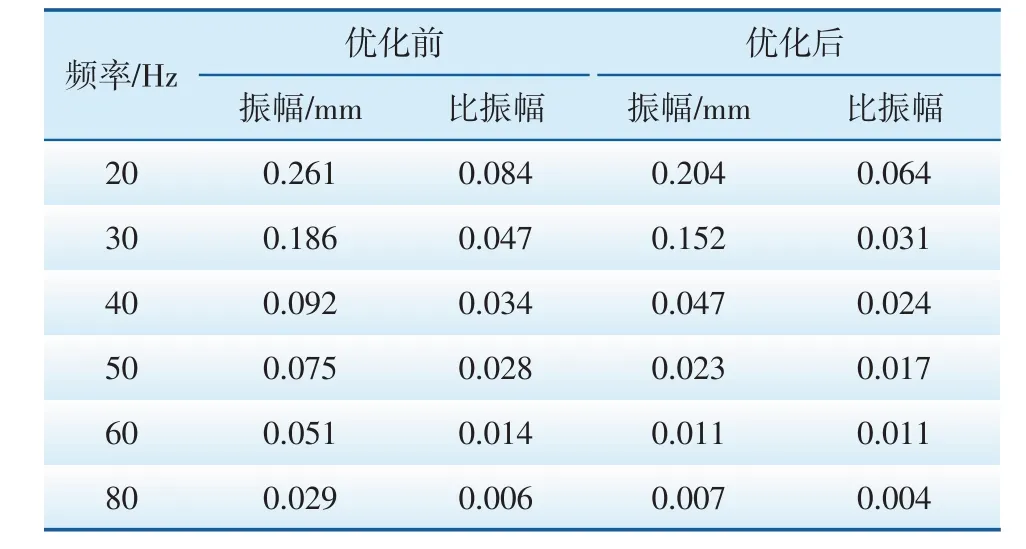
表4 张力为187.7 N时防振锤的功率消耗情况Tab.4 Power consumption of vibration damper(the tension is 187.7 N)

由表4 可知，当张力一定时，在不同频率下，动力学优化后，输电导线的振幅及比振幅值较小，说明防振锤消耗功率较大、防振效果较好。因此，本文提出的防振锤功率特性数值仿真计算与动力学优化在实际应用中具有一定的可靠性。

4 结语

防振锤能够有效地减缓输电导线的振动现象，但是传统的防振锤设计方案无法使其发挥最佳防振性能。本文针对这一问题，对防振锤进行了功率特性数值仿真计算，并根据得到的结果进行了动力学优化。模拟实验结果表明，在频率不同的工况下，相较于优化前，优化后的防振锤功率消耗更大，说明经过动力学优化的防振锤具有更好的防振性能。