基于无网压传感器控制的单相并网逆变器预同步控制策略
2024-03-25刘鉴钧赵爱国杨学林姜伟基
刘鉴钧,齐 军,赵爱国,葛 景,杨学林,姜伟基
(1.内蒙古电力(集团)有限责任公司阿拉善供电分公司,内蒙古 巴彦浩特 750306;2.南京南瑞继保电气有限公司,南京 211102)
0 引言
并网逆变器通常通过测量公共耦合点(Point of Common Coupling,PCC)电压,采用锁相环(Phase-Locked Loop,PLL)跟踪电网相位,从而实现与电网的同步[1-2]。然而,在PCC点的电压测量容易将来自交流电网的谐波引入控制回路,从而威胁系统的稳定性,尤其是在弱电网条件下[3]。另一种与电网同步的方法为无网压传感器的自同步控制策略,通过利用同步发电机的转子运动方程[4],使并网逆变器从外特性上模拟出同步发电机的频率及电压控制特性,产生虚拟“惯量”构成虚拟同步发电机(Virtual Synchronous Generator,VSG)[5-6],相比于采用PLL同步的并网逆变器,基于自同步控制的并网逆变器抑制了PLL 对输出阻抗的影响,呈现出更好的鲁棒性和稳定性[7-8]。
文献[9]提出了一种基于观测器的PCC 点电压估计方法,电流控制器的积分输出用于获得角度误差信号,进而反馈至观测器,其运行原理类似于PLL。在同步旋转坐标下,自同步控制实现比较复杂。此外提出了一种预同步控制策略,在换流器连接到交流电网前,对开关管施加满足一定约束的脉冲,进而通过电流变化速率来估计电网电压。但是通过该方法估计的电网初始相位由于微分算子很容易受到扰动,从而导致相位估计不准确。文献[10]在静止坐标系下提出了一种结合PR 电流控制器的三相并网逆变器自同步控制策略,且该策略同样适用于单相并网逆变器[11]。文献[12]从理论上证明了电流控制器的输出调制波在基频处与PCC 电压的等效性。因此,可以采用电流谐振控制器的输出替代PCC 点电压作为PLL 的输入,且利用电流控制器固有的滤波特性实现并网逆变器在弱电网下的自同步[13-14]。然而,在换流器与电网并网瞬间,由于换流器与电网相位不匹配将导致系统出现较大的冲击电流。预同步控制通过跟踪电网相位从而抑制冲击电流,文献[15]提出了一种基于非线性主动抗扰动的锁相环,可以快速灵活地获取电网相位信息,但是仍需对PCC点电压采样。文献[16-17]在电压型虚拟同步机控制策略的基础上提出了基于虚拟阻抗功率的无锁相环并网预同步控制策略,无需锁相环,通过控制虚拟阻抗上流过的无功功率为零,从而实现了与电网电压频率和相位的预同步。文献[18]针对西藏微网示范电站的多能互补联合供电特性,通过储能型电压源逆变器接入点的电压幅值与频率偏差来调节有功与无功,采用预同步控制降低并网/离网模式切换过程中的冲击电流,提出可以使储能电站灵活离网/并网无缝切换的虚拟同步发电机控制策略。文献[19]针对微电网的并网离网切换问题,通过在微电网交流母线与主电网公共连接点之间引入一个虚拟阻抗,根据两者的电压差和虚拟阻抗计算虚拟电流,然后通过调节虚拟电流为零来实现电压的预同步。
为了解决基于无网压传感器控制的并网逆变器在并网瞬间的暂态冲击问题,本文以单相并网逆变器为研究对象,提出一种无网压传感器的预同步控制策略。规定电流流出逆变器为正,在换流器并网前,通过对开关管施加占空比满足约束的周期性脉冲,使换流器以单位功率因数运行在整流模式,从而换流器输出电流包络线的相位与电网电压的相位相反。与现有的预同步控制方案相比,本文提出的控制器复杂度大大降低,在实际应用中更易实现。
1 基于自同步控制的单相并网逆变器工作原理
采用自同步控制的单相并网逆变器结构如图1所示。该方法与传统控制的本质区别在于锁相环的输入来自于电流控制器输出调制波电压中的分量e,而非PCC点电压VPCC[6]。

图1 基于自同步控制的单相并网逆变器结构图Fig.1 Structural diagram of single-phase grid-connected inverter based on self-synchronization control
根据图1,比例谐振(Proportion Resonant,PR)控制器的传递函数Gc(s)可表示为:
式中:ωn为额定基波角频率
将图1 中的主电路和控制器结合,可以得到采用自同步控制的单相并网逆变器在频域下的数学模型如图2 所示,其中Gdel(s)为延时环节的传递函数,Gp(s)为滤波电感对应的传递函数,其表达式分别为:
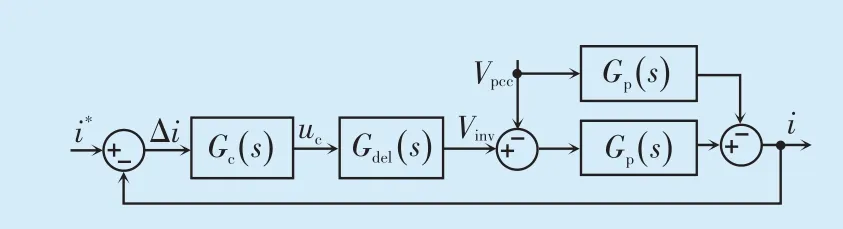
图2 频域下单相并网逆变器数字模型Fig.2 Digital model of the single-phase grid-connected inverter in the frequency domain
式中:Ts为采样周期。
根据图2,基于梅森公式可以得到输出电流i(s)的表达式为:
式中:Go(s) 为逆变器开环传递函数,且满足Go(s) =Gc(s)Gdel(s)Gp(s) 。
根据式(3)可以得到电流误差Δi的表达式为:
图1中电流控制器谐振环节的输出e可表示为:
由式(4)可以得到电流误差Δi 与Vpcc之间的关系为:
将式(6)带入式(5)可以得到e 与Vpcc之间的关系为:
图3 给出了e/Vpcc之间传递函数的伯德图,可以得到在基频处,电流控制器谐振环节的输出e 与PCC点幅值近似相等,相位基本一致,两者在基频处等效。因此,可以采用谐振环节的输出e 作为锁相环的输入,进而跟踪电网的相位。
2 无网压传感器的预同步控制策略
2.1 电感储能及释能回路分析
采用L 型滤波的单相并网逆变器如图4(a)所示,其中L 包含了滤波电感和线路等效电感。图4(b)中,在一个开关周期Ts内,UMS和LMS分别代表上桥臂和下桥臂开关管的调制信号。通过将载波信号与UMS和LMS分别进行比较,可以得到具有恒定占空比的脉宽调制信号,如图4(b)所示,其中G1(G3)代表将脉冲施加到下(上)开关管的阶段,G2代表上下开关管都未施加脉冲的阶段。
如图4所示,在G(1G3)阶段,下(上)桥臂同时导通,电感储存能量,文中规定电流流出逆变器为正,则电流满足:
式中:L为滤波电感与网侧线路电感之和。
根据式(8)可得,当电流初始值为0 时,电流仅取决于电感和电网电压,且可通过施加占空比满足一定约束条件的周期性脉冲使电流初始值为0。根据电网电压的过零点,一个正弦周期可分为两个扇区,分别对应电网电压的正半周和负半周。在每个扇区内的G(1G3)阶段,由于电感储能,电流的绝对值均会增加,且由于电感电流不能突变,换流器在G2阶段将运行于不控整流模式,为电感释放能量提供回路,因此电流绝对值减小。
电网电压正半周内,总是满足E>0,因此根据式(8)可得输出电流i 始终小于0,则在电网电压正半周内,开关管处于G1和G3阶段时的电感储能回路分别如图5(a)和图5(b)所示。在G2阶段,由于电感电流不能突变,因此电流通过上桥臂和下桥臂的二极管与直流侧形成放电回路,电感释放能量,其能量释放回路如图6(a)所示。同理,在电网电压负半周,电流满足i>0,则在开关管处于G1和G3阶段时的电感储能回路分别如图5(c)和图5(d)所示;在G2阶段,其能量释放回路如图6(b)所示。

图5 电感储存能量回路Fig.5 The energy storage circuit of the inductor
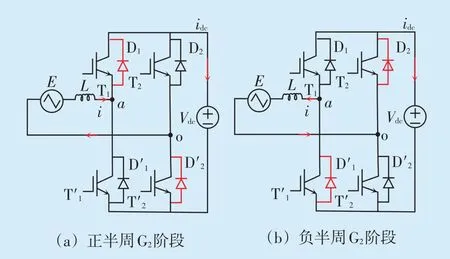
图6 电感释放能量回路Fig.6 The energy release circuit of the inductor
2.2 预同步控制策略可行性分析
图7 给出了在图4(b)所示的周期性脉冲时,相邻开关周期内换流器输出电流特性。在第k个周期内,图7(a)中各点对应的时间表示为:

图7 采用预同步控制后的电流特性.Fig.7 The current characteristics after adopting pre-synchronization control
式中:D为周期性脉冲的占空比;k为开关周期。
图7(a)中,在第k 个开关周期内,n 点的电流值Tn为:
式中:Vg和i0分别代表电网电压幅值和电流的初始值,即o点对应的电流值。
根据图7(a)可知初始电流i0可以表示为:
将式(13)带入式(12)可以得到Tn最终的表达式为:
类似地,图7(a)中,在第k个开关周期内,p点的电流值Tp为:
因此,在每个开关周期内,通过迭代计算点n和点p 处的电流值可以得到估计的电流包络线如图7(b)所示,单相并网逆变器参数如表1所示。根据图7(b)可以得到,由理论推导得到的电流包络线为标准正弦波,相位与电网电压相位相反,且与仿真得到的实际电流i 的包络线完全一致,验证了理论推导的正确性。

表1 单相并网逆变器参数Tab.1 Parameters of the single-phase grid connected inverters
数字控制系统中的每个开关周期内,需要在载波的顶点、底点或顶底点处对实际输出电压或电流采样,其过程如图7(a)所示。根据图7(a)可以得到,在载波的底点对实际电流采样得到采样电流,进而作为控制器的输入,采样电流的值为o 点处的电流值,如式(13)所示。
类似地,在每个开关周期内迭代计算o 点的电流值可以得到估计的采样电流包络线如图7(b)所示,结果表明采样电流也为正弦波,且采样电流的相位与电网电压相位相反。因此,可以通过采样电流来估计电网电压相位,从而实现基于无网压传感器控制的单相并网逆变器的快速可靠并网。
2.3 预同步控制实现过程
为了能得到电流相位从而估计出电网电压相位,采用图8 所示的基于二阶广义积分器的锁相环(Phase-locked Loop Based on Second-order Generalized Integral,SOGI-PLL)获取电流的相位,其中SOGI的详细结构在文献[20]已给出。

图8 预同步过程中的相位估计控制图Fig.8 The block diagram of the phase estimation in the pre-synchronization process
为了实现换流器能平滑并网,在预同步过程中,将通过电流得到的估计相位θe反馈至图1 所示的自同步控制器中,使在预同步过程中,输出相位θ能无误差跟踪估计相位θe,其详细的实现框图如图9所示。

图9 有预同步控制的自同步控制框图Fig.9 Block diagram of self-synchronization control with pre-synchronization control
因此,采用本文所提预同步控制方法的换流器启动过程如下:
(1)对上下开关管分别施加占空比满足一定条件的周期性脉冲;
(2)通过数字控制器对实际电流i进行采样得到采样电流isample;
(3)预同步信号使能(enable),利用SOGI-PLL以采样电流为输入估算电网电压相位,如图8所示;
(4)将估计的相位反馈至自同步控制环,在SOGI-PLL稳定后,自同步控制器投入,有预同步控制的自同步控制框图如图9所示。
3 临界占空比的约束条件
由以上分析可知,采用本文所提预同步控制方法的关键步骤为在周期性脉冲作用在上下桥臂之前,必须保证电流绝对值衰减到0,从而使电感开始储能时的初始电流为0。
根据图7(a)可以得到,在一个开关周期内,p点的电流绝对值最大,因此在每个开关周期内需要保证p 点的电流能衰减到0。为了能得到临界占空比的解析解,在一个开关周期内视电网电压为常数,则p点的电流Tp可表示为:
以正半周为例,p 点电流衰减对应图5(a)所示的放电回路,其对应的电路方程为:
假设p 点电流衰减到0 对应的时刻为t,则t 满足:
根据图7(a)可以得到,为了保证在脉冲施加前电流能衰减至0,放电时间t-tp需满足:
联立式(18)及式(19)可以得到周期性脉冲的占空比需满足的约束条件为:
根据式(16)所示的p 点电流表达式,Tp绝对值与电网电压幅值正相关,所以在正半周期,当电压绝对值最大,即在第π(/2ωTs)+1个周期时,Tp绝对值最大,此时根据式(20)得到的D 为临界值。根据表1 给出的逆变器参数,在第51 个开关周期内Tp绝对值最大,且D的临界值为0.2933。由于正半周和负半周电网电压是对称的,区别仅在于电流方向不同,因此D的临界值是一致的。
4 实验验证
为验证所提预同步控制策略的有效性,本节对通过半实物实验平台搭建了图1所示的逆变器系统模型,实验参数如表1 所示,其中开关频率fs提高至10 kHz。
4.1 电流特性验证
图10(a)为对采用L 型滤波的单相并网逆变器施加占空比为0.25 的周期性脉冲后系统的输出特性。从图10(a)可以看出,实际电流i的包络线和采样电流isample的相位与电网电压相位相反,验证了理论分析的正确性。图10(b)给出了在相同条件下,单相并网逆变器采用LCL型滤波器时的系统输出特性,其中滤波电容Cf=100 μF。从图10(b)可以看出系统的输出特性与采用L型滤波器的并网逆变器一致,即满足采样电流的相位与电网电压相位相反,说明滤波器类型不会影响所提预同步控制策略的有效性。

图10 采用不同滤波器类型的单相并网逆变器输出特性Fig.10 Output characteristics of the single-phase grid-connected inverters using different types of filters
4.2 占空比验证
图11 为不同占空比下单相并网逆变器的输出特性,从图11(b)可以看出,当占空比超过临界占空比0.2933后,不能保证在每个开关周期内在周期性脉冲施加之前电流衰减到0,进而导致实际电流的包络线和采样电流的相位不再与电网电压相反,验证了临界占空比约束推导的正确性。
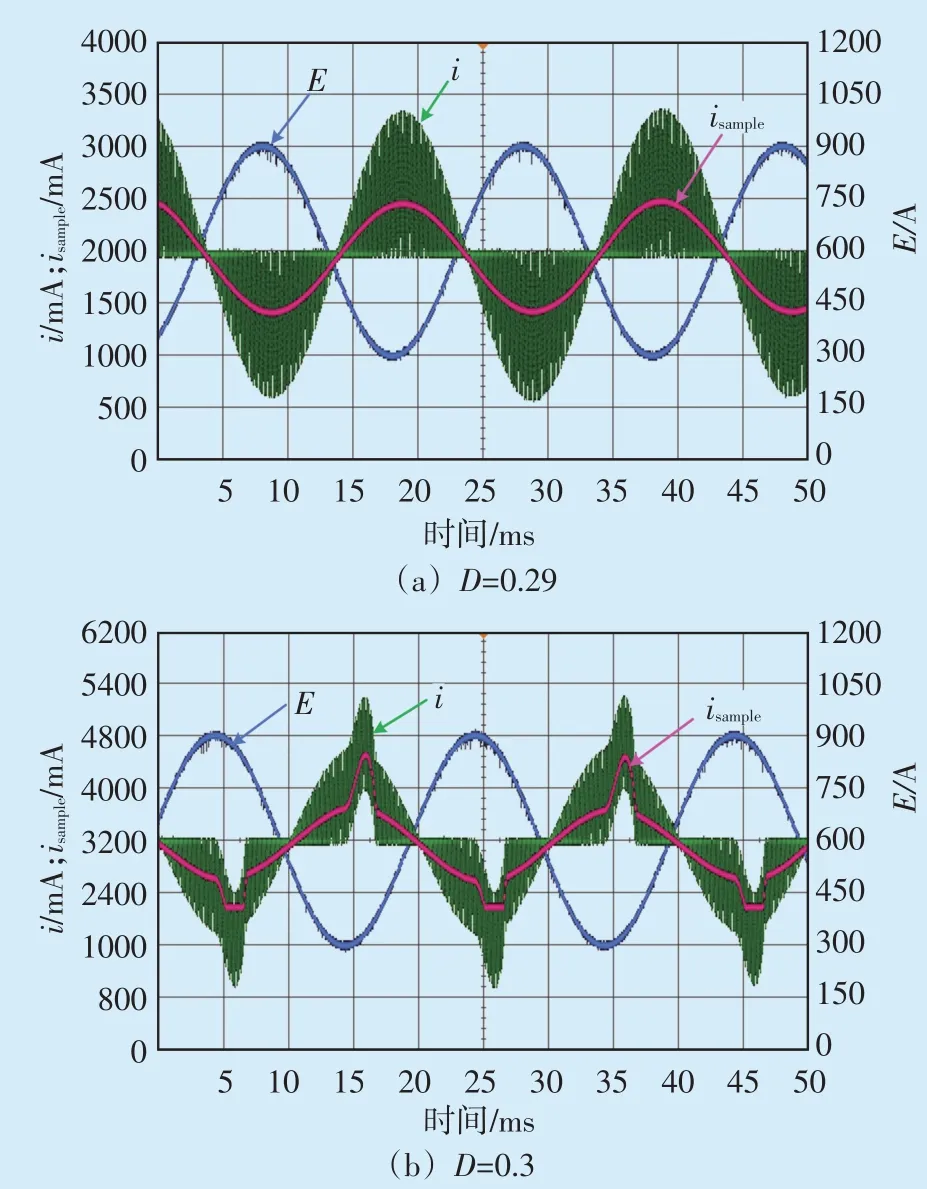
图11 不同占空比下单相并网逆变器的输出特性Fig.11 Output characteristics of the single-phase grid-connected inverters under different duty cycles
4.3 预同步控制策略有效性验证
图12 给出了基于自同步控制的单相并网逆变器有无预同步控制的输出特性,其中d轴和q轴电流参考值分别为30 A和0,且系统的保护动作电流为2倍额定电流。从图11(a)可以看出,没有预同步控制策略的逆变器在控制器投入瞬间,冲击电流超过60 A,导致系统保护动作,系统停止运行。而采用本文所提预同步控制策略后的并网逆变器输出特性如图11(b)所示,当换流器从整流模式切换到采用自同步控制的逆变器控制模式后,换流器能平滑可靠地并入电网,显著改善了并网瞬间的初始暂态性能。

图12 基于自同步控制的单相并网逆变器有无预同步控制的输出特性Fig.12 Output characteristics of single-phase grid-connected inverter based on the self-synchronization control with and without pre-synchronization control
5 结语
本文以基于自同步控制的单相并网逆变器为研究对象,围绕换流器并网瞬间的冲击电流问题,提出一种无网压传感器的预同步控制策略,并对该方法的工作原理及可行性进行了分析。通过半实物实验测试,对所提的预同步控制策略进行实验验证,理论和实验结果表明,本文所提控制策略结构简单,仅通过施加占空比满足一定约束条件的周期性脉冲,采用PLL 检测采样电流相位就能实现对电网电压的估计。同时,所提控制器具有很好的鲁棒性,且所提方法与滤波器类型无关。采用本文所提的预同步控制方法能减小换流器在并网瞬间的冲击电流,使换流器能可靠平滑地并入电网,且具有很好的初始瞬态。与现有的预同步控制方案相比,本文提出的控制器复杂度大幅降低,且无需电网电压传感器,节约了硬件成本。
