Theoretical investigations of population trapping phenomena in atomic four-color,three-step photoionization scheme

Xiao-Yong Lu(卢肖勇) and Ya-Peng Sun(孙亚鹏)

1Science and Technology on Particle Transport and Separation Laboratory,Tianjin 300180,China

2Department of Engineering Physics,Tsinghua University,Beijing 100084,China

Keywords: population trapping,metastable state,selective photoionization,laser bandwidth

1.Introduction

The atomic multi-step photoionization process, a critical part of the laser isotope separation(LIS)process,[1]is the only source of selectivity.Meanwhile,it has various applications in laser resonance ionization mass spectroscopy (LRIMS),[2-4]single atom(molecule)detection,[5,6]and chemical dynamics studies.[7]Evaluating laser-atom interaction dynamics and optimizing the process parameters have attracted the attention of many scientists towards efficient selective ionization.The three-color, three-step photoionization scheme plays a significant role in the previous studies.[8-13]Besides, atoms may be populated in a metastable state because of intense collisions in the electron beam metal evaporation process.For example, 50% and 30% of uranium atoms populate the ground state (0 cm-1) and the first metastable state (620 cm-1), at a typical evaporation temperature of 2800 K.Other elements,such as lutetium,neodymium nickel,and stannum,which are hard to evaporate,display similar properties.[14,15]Metastable state populations can be used for the economy unless the transition from metastable state to ionization regime is prohibited or the population is inappreciable.However, the population trapping effects may be possibly generated considering the metastable state.[16,17]The energy conservation in the transition between the ground and metastable states may harm the excitation processes.[18]Most of population-trapping researches concentrate in monochromatic laser fields.[19-21]Since appreciable laser line width is inevitable in practical applications of LIS,[22]consideration of metastable state in a non-monochromatic laser field makes atomic multi-step photoionization study more practical and applicable for specific elements.

In this work, the density matrix formalism is used to study a hypothetical atomic four-color, three-step photoionization process.Firstly, the semi-classical differential equations of photoionization are established with the consideration of metastable state and laser bandwidth.Secondly, the population trapping phenomena in monochromatic laser field and non-monochromatic laser field are compared.Thirdly, influences of various process parameters on the selective ionization effect are investigated numerically, and optimized conditions are obtained.Lastly, some conclusions are drawn from the present study.

2.Theoretical basis

In this section,the atomic four-color,three-step photoionization process is described by density matrix theory.In the LIS process, isotope A and isotope B are the target isotope and non-target isotope, respectively.As shown in Fig.1, the ground,metastable,the first-and second-excited states are denotes as|1〉,|4〉,|2〉, and|3〉 respectively.Four bound levels below the ionization potential are coupled by three laser pulses coherently, whereas the transition|3〉→auto-ionization state is coupled by a third laser pulse incoherently, and the autoionization rateRis introduced to substitute for the effect of the third laser.[1,23]

Fig.1.Schematic diagram of atomic four-color,three-step photoionization process.Isotopes A and B are distinguished by the energy shift of the first-and second-excited states.

The wave functionΨof a single atom can be regarded as the superposition of four states under the excitation of lasers,and expressed as

whereamandΦmare the probability amplitude and eigenvalue function of state|m〉.Under the rotating-wave approximation(RWA),electric dipole approximation,and adiabatic approximation,the differential equations of probability amplitude are written as

The Rabi frequency isΩm(m=1, 2, 4), proportional to the laser pulse’s electric amplitude and atomic electric dipole moment,andΔm(m=1,2,4)is the detuning of laser frequency relative to atomic transition frequency.

Probability amplitudes are replaced by density matrix elementsρmn=am·a*n(m,n=1,2,3,4)based on Eqs.(2)-(5).Besides,the spontaneous decaysΓ2andΓ3from excited states are introduced into the time-varying equations and given as

Laser bandwidth in the non-monochromaticity is introduced through the phase diffusion model in Eqs.(6)-(18), as additional diffusion terms of the off-diagonal decay rates, wherebmis the full width at half maximum(FWHM)value of laser bandwidth.[23,24]The laser spectrum displays a Lorentzian profile in nearly resonant circumstances but turns into quasimonochrome in a far-off-resonant condition.The spectrum can be adjusted by changing the cut-off coefficientβin numerical simulations.[25,26]

A vectorρ, which contains sixteen density matrix elements and the ionization probabilityρion,is introduced to describe Eqs.(6)-(17)succinctly,

whereQis the coeffciient matrix.

The selectivity factorSis defined as the ionization probability ratio of target isotope A to non-target isotope B,

The general ionization effect in metal vapor is integrated over all Doppler-induced detunings,and defined as

wherefD(Δ) is the Doppler broadening of metal vapor in the laser propagation direction.The population trapping effect is defined as the difference between total ionization probability and the sum of ionization probabilities of“laser 1+laser 2+laser 3”and“laser 4+laser 2+laser 3”,

3.Results and discussion

Numerical simulations of atomic four-color, three-step photoionization processes are carried out in this section.The four-order Runge-Kutta algorithm is adopted to solve the differential equations.The simulation parameters of isotope particles and lasers are listed in Tables 1 and 2,respectively.The typical lifetime of a metastable state is generally on the order of a microsecond or millisecond,which is long enough to neglect the decay of the metastable state.It should be noted that the isotope shifts, laser frequency detuning, and bandwidths are all expressed in angular frequencies.If one changes in a specific range, others are default values unless otherwise stated.

In Subsection 3.1,the ionization properties of four-color,three-step photoionization processes in various circumstances are compared.Then,the population trapping effects with and without bandwidth are discussed in Subsection 3.2.Lastly,critical process parameters at a specific bandwidth are optimized in Subsection 3.3.

Table 1.Simulation parameters of isotopes.

Table 2.Simulation parameters of lasers.

3.1.Photoionization properties

The time evolutions of population probabilities and ionization probability of target isotope A are studied in monochromatic and non-monochromatic laser fields, and the results are shown in Fig.2,where the simulations in Figs.2(c)and 2(d) are carried out without laser 4.Population probabilities of bound states display intense Rabi oscillations in monochromatic laser fields, and the ionization probability drops when laser 4 exists.The population trapping remains part of the atoms in the transitions|2〉→|1〉 and|2〉→|4〉,which are more than those atoms induced by laser 4, compared with the population probability of the states|1〉,|2〉,and|4〉 in Figs.2(a) and 2(c).[23]The effects visibly weaken the ionization process,owing to the degradation ofρ13andρ23in Eqs.(12) and (15).Therefore, the number of ionized atoms,namely the final ionization probability in Fig.2(a), is lower than that in Fig.2(c).Laser 4,which connects the metastable state and the first-excited state, is harmful to final ionization probability in monochromatic excitation fields.[27]

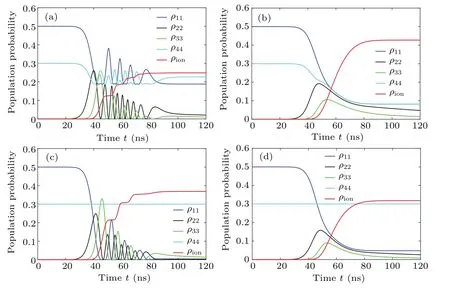
Fig.2.Variations of population probability of target isotope with time under several conditions.Time-dependent intense Rabi oscillations in monochromatic fields (a) with and (c) without laser 4.Time-dependent ionization probability ρion (b) with and (d) without laser 4 in non-monochromatic fields.

The coherent interactions between bound states deteriorate sharply, and Rabi oscillations are damped in nonmonochromatic excitation circumstances.As a result, the population probabilities vary gradually and monotonically as shown in Figs.2(b) and 2(d).When the metastable state is considered, the ionization probability for the case of nonmonochromatic field is higher than that in monochromatic laser field due to the diminishment of population trapping with a bandwidth of 1.0 GHz in Figs.2(a) and 2(b).Nevertheless, the population trapping effect still has an effect on nonmonochromaticity because the final ionization probability is not proportional to the number of initial atoms as shown in Figs.2(b)and 2(d).

3.2.Population trapping effects

Fig.3.Influences of laser bandwidth on(a)ionization probability and(b)population trapping effects in four-color,three-step photoionization process.

The population trapping phenomena and its crucial factors in atomic four-color, three-step photoionization are investigated numerically in this subsection.The population trapping effects,defined by Eq.(23),are negatively correlated with efficient laser excitation, reflecting the formation of coherent superposition states that are unable to excite.Figure 3 shows the influences of bandwidths of laser 1 and laser 4 on ionization probability and population trapping.The results show that ionization probability rises rapidly when the laser bandwidth is less than 0.2 GHz,and remains stable at a higher laser bandwidth.The rise can be explained as the sharp reduction of the population trapping effects as shown in Fig.3(b).Accordingly,there is an appropriate bandwidth in which more atoms can escape from the population trapping state to the second-excited state|3〉,and then be ionized.

The influences of the process parameters of laser 1 and laser 4 on the ionization probability of the target isotope are simulated,and the results are shown in Figs.4-6,corresponding to Rabi frequency,relative time delay,and laser frequency detuning, respectively.Numerical results are presented in monochromatic and non-monochromatic laser fields, where the green point denotes the typical simulation condition and the red line represents the ionization probability contour equal to the typical simulation condition.Therefore,the domain encapsulated by the red line displays a better ionization effect than in the typical condition.

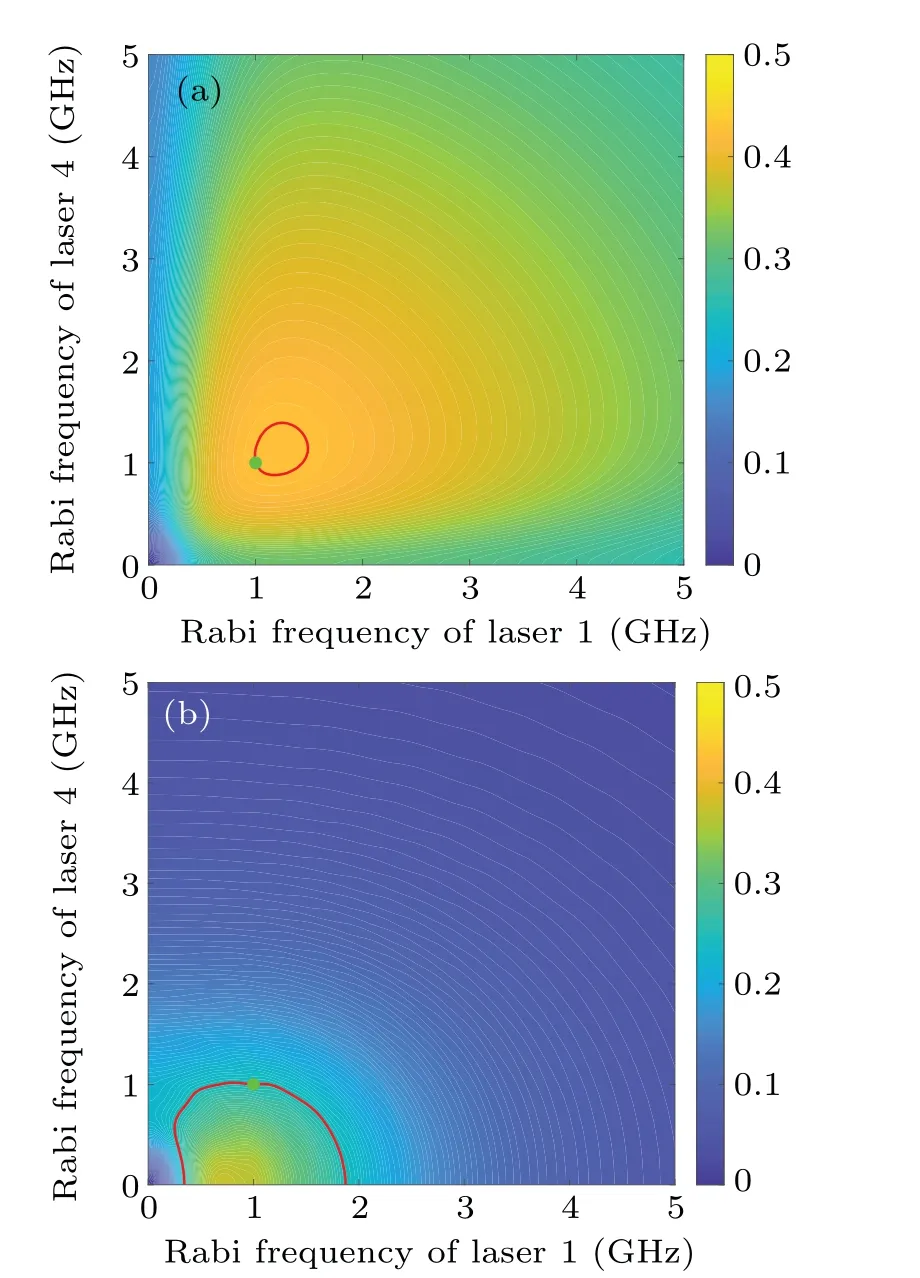
Fig.4.Influences of Rabi frequency on ionization probability of target isotope: (a)the Rabi frequency of laser 1 and laser 4 plays an identical role in ionization probability in non-monochromatic field,(b)involved laser 4,excited laser of metastable state,reduces ionization probability in monochromatic field.

The ionization probability can obtain a slight increase by adjusting Rabi frequency or relative time delay in nonmonochromatic fields,whereas the properties are quite different in monochromatic fields.It can be observed that the initial Rabi frequencies of laser 1 and laser 4 are slightly unsaturated in non-monochromatic field as shown in Fig.4(a).However,the ionization probability is likely to reach the highest points with a low Rabi frequency of laser 4 due to the population trapping phenomena and the disproportion of initial particles at a narrow bandwidth.

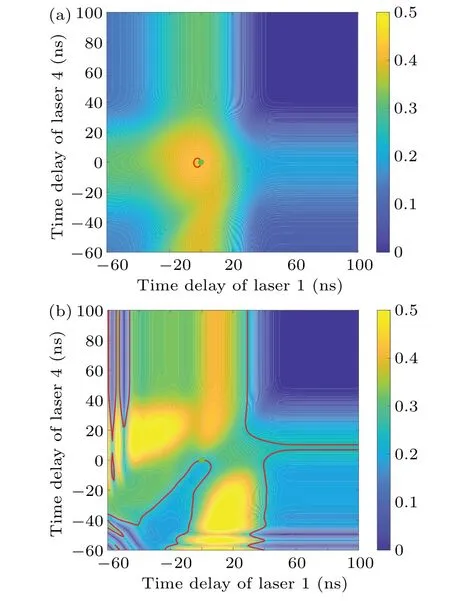
Fig.5.Influences of relative time delay on ionization probability of target isotope in (a) non-monochromatic field and (b) monochromatic field.The ionization probability with time delay has the same period as the Rabi oscillation when one laser arrives much earlier(at least 40 ns earlier)in monochromatic field.

In addition, any adjustment of the relative time delay of laser 1 or laser 4 will lead to a decrease of ionization probability in non-monochromatic excitation field,except that laser 1 arrives slightly earlier as shown in Fig.5(a).The ionization probability can be significantly enhanced by adjusting the relative time delay or laser frequency detuning under monochromatic field, which means that the population trapping effects are weakened in specific conditions, especially when two lasers are asynchronous or non-resonant.For example, if either laser arrives earlier, the ionization probability will increase, because the population trapping effects will not appear soon under asynchronous conditions as shown in Fig.5(b).Otherwise,the ionization probability with time delay has the same period as the Rabi oscillation when the arrival time of one laser arrives much earlier (at least 40 ns earlier),and it is almost independent of the arrival time of another laser.The reason is that the ionization probability is directly related to the population of the first excited state at the arrival moment of laser 2 and laser 3.In contrast,Rabi oscillation has already been induced by the arrival of laser 1 or laser 4.Furthermore,when laser 1 lags far behind the other three lasers,the ionization probability is lower than that in typical conditions since the power densities of the other lasers are underutilized.

Similar phenomena appear in frequency-adjusting results as shown in Fig.6(b).Ionization probability remains high even though laser 4 is non-resonant.That is, atoms populated in metastable states cannot easily be trapped in transition 2|〉→|4〉.There appears to be a visible decline of ionization probability when(Δ1+Δ4)equals zero as shown in the zoomin area in Fig.6(b).The reason is that the population trapping is induced sharply whenΔ1+Δ4≈0 since the large oscillation ofρ14in Eq.(13) has the minimum damping, which is consistent with previous results.[28-30]The phenomena in non-monochromatic excitation field demonstrate that any adjustment of frequency detuning of laser 1 or laser 4 can cause the decline of ionization probability, which is easy to understand,as shown in Fig.6(a).

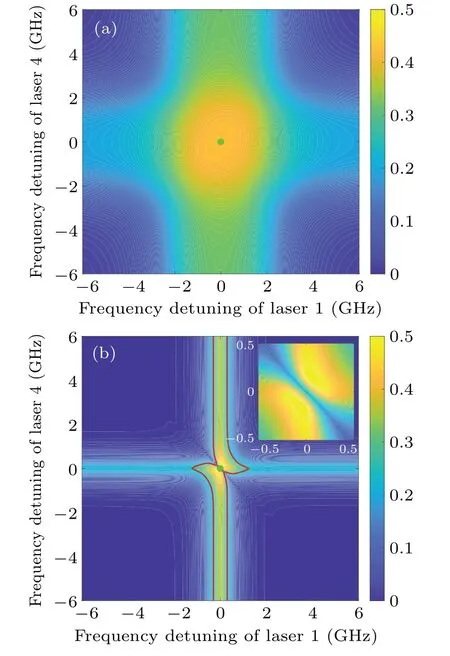
Fig.6.Influences of laser frequency detuning on ionization probability of target isotope in(a)non-monochromatic field and(b)monochromatic field.A visible decline of ionization probability occurs when(Δ1+Δ4)equals zero in monochromatic field.

However, the reality is that high laser power density and narrow laser bandwidth cannot be obtained simultaneously in exploratory applications.Considering laser bandwidth,the coherent interaction and population trappings will be weakened.The enhancement of the ionization effect is uneasy by repressing or avoiding the population trapping phenomena in the atomic four-color, three-step photoionization process.[26,27]Therefore, studies in non-monochromatic laser fields make more practical significance in LIS experiments.

3.3.Parameter optimization

Figure 7 provides the influences of laser process parameters,including Rabi frequency,laser bandwidth,frequency detuning, and time delay, on population trapping effect in nonmonochromatic laser field.The influences of the above parameters on the ionization probability are plotted in Figs.3(a),4(a), 5(a), and 6(a).Generally, population trapping phenomena appear quickly under intense laser excitation circumstances; active interaction between atom and laser is sufficiently solid and coherent.Most of the influences of time delay on selective ionization can be equivalent to those of Rabi frequency.[23]In addition,as shown in Figs.7(a)and 4(a),the Rabi frequency of the first-step laser should not be set much higher than the other one.

The relationship between the selectivity factor and ionization probability is shown in Fig.8,where the green domain stems from simultaneous adjustment of “laser 1+laser 2”,the red domain arises from simultaneous adjustment of“laser 1+laser 4”,and the blue points represent the results under typical condition.The adjustment ranges of laser process parameters are listed below: Rabi frequencies, bandwidths,frequency detuning, and time delays (relative to laser 3)of three relevant lasers are 0.0 GHz-5.0 GHz, 0.0 GHz-10.0 GHz,-6.0 GHz-+6.0 GHz, and-60 ns-+100 ns, respectively.The results beyond these ranges have little practical reference.In addition, it is worth noting that only data in the top right corner of the graphs provide practical values.

For the four-color, three-step photoionization process, it is obvious that there are two ladder-type three-level structures and one Lambda-type three-level structure.Hence, the combination of “laser 1+laser 2” and “laser 1+laser 4”, corresponding to two different structures, are sufficient to explain the trend of selectivity and ionization probability with various parameters.The overall properties of “laser 1+laser 4” are similar to those of “laser 1+laser 2”, which were discussed systematically in our previous studies.[23,31]Nevertheless,according to Fig.8, it is quite difficult to improve ionization probability and selectivity factor simultaneously by adjusting Rabi frequency, frequency detuning, or time delay.Except for laser bandwidth, the increase of selectivity factor will inevitably result in insufficient excitation from the top-right contour of colored domains, as shown in Fig.8(b).If any laser(especially laser 2) bandwidth is used in a specific range, the ionization probability and selectivity factor will increase simultaneously.The reason is that laser 2 displays milder population trapping and weaker power density saturation at identical excitation Rabi frequency than the two first-step lasers.Also,it should be noted that when the bandwidths of two firststep lasers are adjusted,there appears a critical point that can imbalance the population trapping and active coherent excitation.

Fig.8.Selectivity versus ionization probability when (a) Rabi frequency, (b) laser bandwidth, (c) frequency detuning, and (d) relative time delay are adjusted.Only the data on the top right corner of the graphs provide practical values.There is a tradeoff between ionization probability and selectivity.

In the industrial-scale quantity LIS process,considerable Doppler broadening of atomic vapor occurs due to violent interatomic collisions and extended geometric design.[32]The influence of atomic Doppler broadening is plotted in Fig.9,where the ionization probability of the target isotope, population trapping effects, and selectivity are all presented.The general ionization effect is defined by Eq.(22),and the atomic energy structural diagram including ladder-type and Lambdatype structures is shown in Fig.1.Overall, atomic Doppler broadening has similar effect on ionization probability to laser bandwidth,which is consistent with previous results.[33]

Fig.9.Influence of atomic Doppler broadening on selective photoionization.Doppler broadening reduces the ionization probability and selectivity.

Since the typical FWHM value of Doppler broadening is bout 1.0 GHz in this study,selective ionization displays almost identical effects to those under Doppler-free conditions.

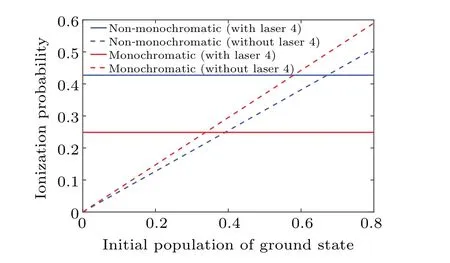
Fig.10.Relations between ionization probability and initial population of the ground state.The involved metastable state may reduce the ionization probability in the regions where the dashed line is higher than solid line.

Since the population ratio between the ground state and the metastable state can be transformed by heating or other treatments, the initial population of the ground state is another critical parameter in a four-color, three-step photoionization scheme,whose influences are plotted in Fig.10,where ionization probabilities are obtained in monochromatic condition and non-monochromatic condition,sum populations of the ground state and the metastable state at each point are the same.The results show that monochromatic lasers perform better than non-monochromatic ones when laser 4 is not involved.Higher spectral power density (SPD) at the resonant frequency can be obtained in the monochromatic field to complete excitation.On the contrary, higher ionization probability can be obtained when the lasers are at a specific bandwidth with the existence of the metastable state, which has been thoroughly discussed above.Besides, the utilization of a metastable state may have a negative influence when the ground state population is above the limit value,implying that the bandwidth plays a more prominent role.

4.Conclusions

Atomic four-color, three-step photoionization processes are studied numerically for efficient selective photoionization.In this work,Density matrix equations considering metastable state and laser bandwidth are established.Time evolution results show that population trapping effect occur intensely in monochromatic excitation field,while it gradually turns weak as the laser bandwidth increases.It is hard to improve the ionization probability by repressing population trapping phenomenon in non-monochromatic field.Besides,parameter optimization results show that it is difficult to simultaneously improve ionization probability and selectivity factor by adjusting Rabi frequency, frequency detuning, or time delay individually.Ionization probability and selectivity factor rise if any laser bandwidth is used in a specific range.Besides, the utilization of metastable state may play a negative role when its population is low enough.